飞行模拟转台非线性干扰观测器反步滑模控制器设计
常 诚, 常雅男, 艾 飞
(1.火箭军驻六九九厂军事代表室,北京 100039; 2.中国人民解放军61660部队,北京 100039)
飞行模拟转台非线性干扰观测器反步滑模控制器设计
常 诚1, 常雅男2, 艾 飞1
(1.火箭军驻六九九厂军事代表室,北京 100039; 2.中国人民解放军61660部队,北京 100039)
针对考虑非线性摩擦、参数不确定性和电机力矩波动等不确定干扰的飞行模拟转台伺服系统鲁棒跟踪控制问题,提出了一种基于非线性干扰观测器的自适应反步全局滑模变结构补偿控制方案;该方案采用反步控制方法设计转速期望虚拟控制,然后利用非线性干扰观测器观测系统复合不确定性干扰,在此基础上,对引入非线性干扰观测器的系统设计自适应全局滑模变结构控制器,实现了飞行模拟转台伺服系统期望转角信号的鲁棒跟踪控制;通过Lyapunov稳定性理论证明了闭环系统全局渐进稳定,且系统跟踪误差渐进收敛到零;仿真研究了非线性摩擦对飞行模拟转台伺服系统性能的影响,对比了高增益PD补偿控制方法与基于非线性干扰观测器的自适应反步全局滑模变结构控制方法的控制效果。
非线性干扰观测器;反步滑模控制;飞行模拟转台;不确定干扰
0 引言
飞行模拟转台[1]是对飞机、导弹、卫星等有关运动体的高精尖仿真实验设备,可以在实验室条件下真实地模拟飞行器在空中飞行时的各种姿态,获得实验数据。飞行模拟转台伺服系统设计是系统控制精度的重要保证。但是由于非线性摩擦环节的存在,使得高精度伺服控制系统中的动态及静态性能受到很大程度的影响[2-3]。此外,系统还易受到参数不确定性、未建模动态和外界扰动负载力矩等不确定因素的影响,使得系统跟踪精度显著下降。因此,对飞行模拟转台伺服系统进行非线性摩擦补偿及控制方法研究就显得尤为重要。
关于飞行模拟转台伺服系统的摩擦补偿及控制问题,一些学者已做了相关的研究和实验,如:刘金琨等[4]采用定量反馈控制方法补偿非线性摩擦带来的影响,研究飞行模拟转台伺服系统的鲁棒跟踪控制问题;文献[5]将重复控制方法应用到飞行模拟转台伺服系统的周期指令信号鲁棒跟踪控制;李飞等[6]提出了一种基于自适应粒子群算法的飞行模拟转台伺服系统的优化控制策略。然而,由于上述文献均采用经典的静态非线性Stribeck摩擦模型,无法真实地反映摩擦现象的动态过程,因此,在高精度飞行模拟转台伺服系统摩擦补偿控制中,并不能获得满意的结果。
本文针对飞行模拟转台伺服系统存在未知非线性摩擦和不确定干扰情况下的鲁棒跟踪控制问题,提出了一种基于非线性干扰观测器[7-8]的反步滑模控制方案。该方案首先采用反步控制方法设计转速期望虚拟控制,然后采用非线性干扰观测器观测由非线性摩擦、参数不确定性和外界扰动负载力矩等构成的复合不确定干扰,进而对引入非线性干扰观测器的系统设计自适应全局滑模控制器,以保证飞行模拟转台伺服系统具有良好的跟踪性能和较强的鲁棒性。通过Lyapunov理论证明了闭环系统全局渐进稳定,且系统跟踪误差渐进收敛到零。
1 飞行模拟转台伺服系统模型
考虑非线性摩擦的飞行模拟转台伺服系统结构如图1所示。

图1 飞行模拟转台伺服系统结构

根据伺服系统结构,得到如下的简化控制系统动态方程:
(1)

(2)

将式(2)整理成如下形式:
(3)

基于非线性干扰观测器设计自适应反步全局滑模补偿控制器,使得系统输出y=θ能够稳定跟踪参考指令信号yd=θd,同时保证闭环系统全局渐进稳定。
2 控制器设计
控制器设计包含2步:第1步,基于反步控制方法设计转速期望虚拟控制α1;第2步,采用非线性干扰观测器观测作用在转速子系统的复合不确定干扰M,经过增益调整环节,得到为克服复合不确定干扰M所需要的控制量uM,与采用自适应全局滑模控制方法设计得到的控制律ubg共同作为整个系统的控制器u。系统控制结构如图2所示。
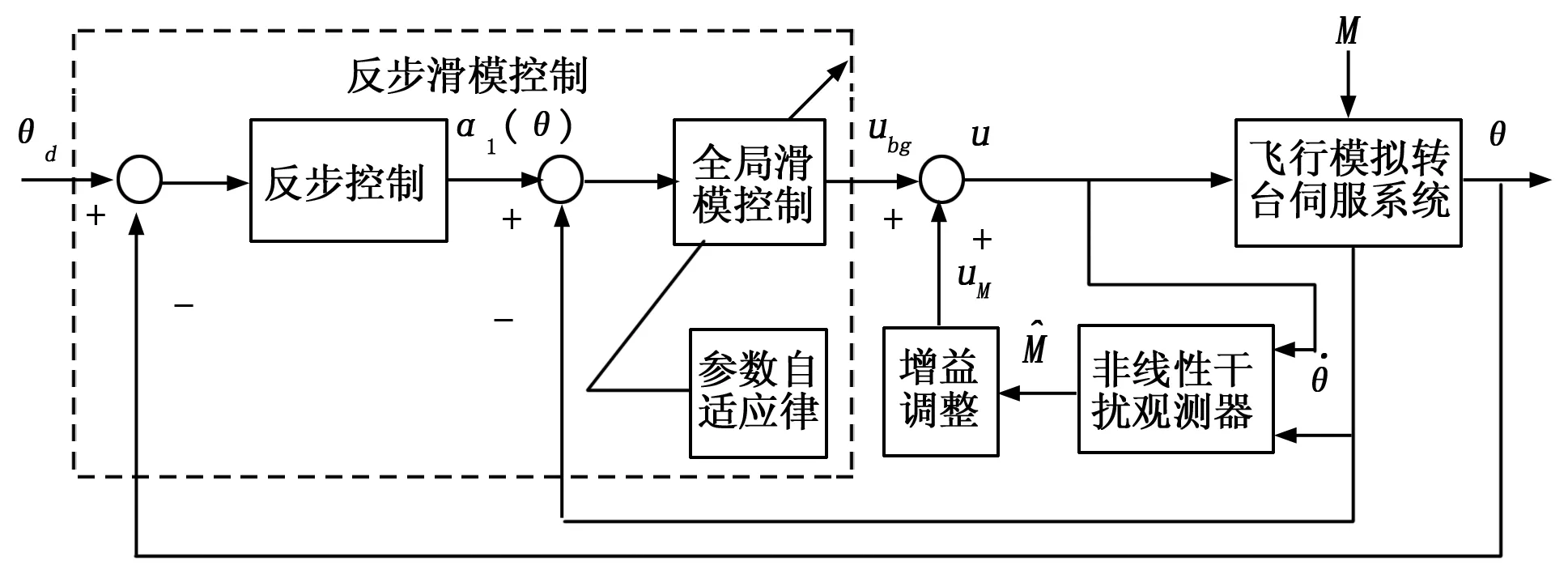
图2 系统控制结构
首先定义闭环系统(3)的状态跟踪误差为:
(4)
式中,α1为转速子系统的期望虚拟控制。
第1步:由闭环系统(3)的转角子系统和转角跟踪误差e1=x1-yd,则e1的动态方程为:
(5)
根据式(5)可设计转速期望虚拟控制为:
(6)
式中,k1>0为设计参数。将转速期望虚拟控制α1代入式(5),则e1的动态方程为:
(7)
第2步:由闭环系统(3)的转速子系统和转速跟踪误差e2=x2-α1,则e2的动态方程为:
(8)
由于存在复合不确定干扰M,故采用非线性干扰观测器观测M,即:
(9)
式中,h>0为设计参数。

(10)

定义全局滑模面:
s=c1e1+e2-g(t)
(11)
式中,c1>0为设计参数,g(t)是为了满足全局动态滑模而设计的非线性函数,且满足:g(0)=c1e1(0)+e2(0);t→∞时,g(t)→0;g(t)一阶可导。因此,系统滑模面s在t=0时刻即收敛到零,消除了滑模的趋近模态。对s求导可得:
(12)
则设计控制律和参数自适应律为:
(13)

(14)
式中,k2>0为控制增益,γ>0为自适应增益系数。
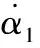
3 稳定性分析
定理1:针对存在非线性摩擦、参数不确定性和电机力矩波动等不确定干扰的飞行模拟转台伺服系统,基于非线性干扰观测器(9),选取全局滑模面(11),设计控制律(13)和参数自适应律(14),使得闭环系统全局渐进稳定,通过选择适当的设计参数,跟踪误差渐进收敛。
证明:定义闭环系统(3)的Lyapunov函数为:
(15)
(16)
将式(13)代入式(16)可得:
(17)
将自适应律(14)代入式(17)可得:
(18)
令:
(19)

因此,总可以选取适当的设计参数k1,k2,c1满足-ΞTQΞ≤0,则:
(20)

(21)
则:
(22)
因为V(e1(0),e2(0),s(0))有界,V(e1(t),e2(t),s(t))是单调有界非增函数,故:
V(e1(∞),e2(∞),s(∞))
(23)

(24)
则当t→∞时,e1→0,e2→0,s→0。
4 仿真与分析
为了真实地反映飞行模拟转台伺服系统运行过程中的非线性摩擦现象,仿真中采用LuGre动态摩擦模型[9]。LuGre摩擦模型的数学表达式可描述如下:
(25)
(26)
(27)
各参数的含义和仿真中使用的数值如表1所示。

表1 LuGre摩擦模型参数设定
为研究非线性摩擦对飞行模拟转台伺服系统性能的影响以及验证本文控制方案的有效性,分别采用高增益PD补偿控制(PDC)和基于非线性干扰观测器的自适应反步全局滑模补偿控制(NDO+ABGSMVSC)进行仿真对比,完成控制性能的对比分析。
飞行模拟转台伺服系统模型参数为:Ku=11,R=7.77 Ω,Km=6(N·m/A),J=0.6(kg·m2),Ce=1.2(V/rad·s-1)。模型参数不确定性和电机力矩波动引起的不确定干扰用幅值为5的正弦波5sin(t)代替。参考指令信号yd=0.5 sin(πt),初始状态x0=[-0.5,0]T。
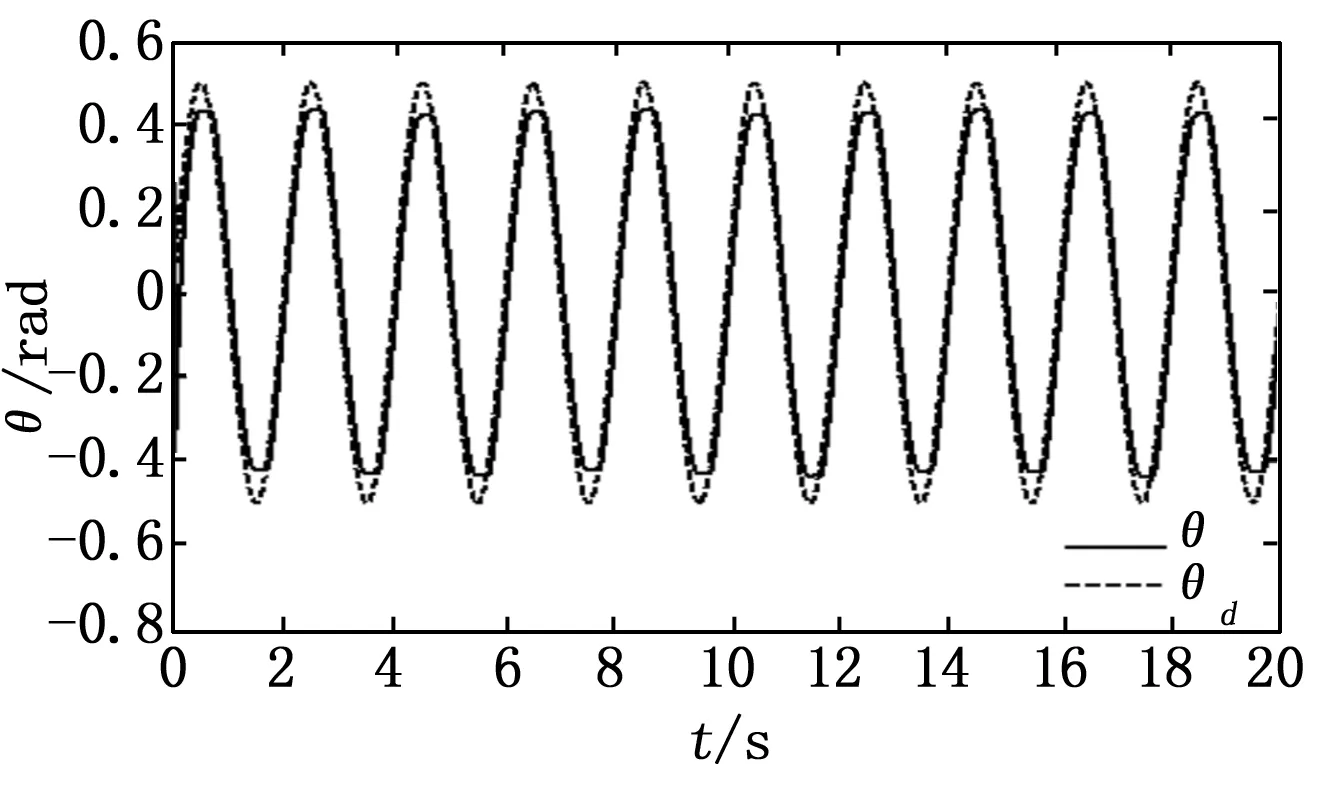
图3 实际转角q与期望转角θd(PDC)

图4 控制电压p(PDC)


图5 实际转角φ与期望转角θd(NDO+ABGSMVSC)

图6 控制电压u(NDO+ABGSMVSC)
5 结论
本文针对考虑不确定性的飞行模拟转台伺服系统,提出了一种基于非线性干扰观测器的反步全局滑模补偿控制方法。该方法采用反步控制方法设计转速期望虚拟控制,然后利用非线性干扰观测器观测系统不确定干扰,进而对引入非线性干扰观测器的系统设计自适应全局滑模控制器。通过与采用高增益PD补偿控制(PDC)和基于非线性干扰观测器的自适应反步全局滑模补偿控制(NDO+ABGSMVSC)进行仿真对比,结果表明,本文方法实现了飞行模拟转台伺服系统期望转角信号的鲁棒跟踪控制,具有较好的控制性能。

图7 实际干扰M及其观测值β
[1] 刘金琨, 尔联洁. 飞行模拟转台高精度数字重复控制器的设计[J]. 航空学报, 2004, 25(1): 59-61.
[2] 刘 强, 尔联洁, 刘金琨. 摩擦非线性环节的特性、建模与控制补偿综述[J]. 系统工程与电子技术, 2002, 24(11): 45-52.
[3] 朱 勇, 姜万录, 郑 直. 摩擦力作用下电液伺服系统非线性动力学行为[J]. 北京航空航天大学学报, 2015, 41(1):50-57.
[4] Liu J K,Er L J. QFT robust control design for 3-axis flight table servo system with large friction[J]. Chinese Journal of Aeronautics, 2004, 17(1): 34-38.
[5] 刘金琨, 尔联洁. 飞行模拟转台高精度数字重复控制器设计[J]. 航空学报, 2004, 25(1): 59-61.
[6] 李 飞, 胡剑波, 郑 磊,等. 飞行模拟转台的反推滑模控制优化设计[J]. 微特电机, 2015, 43(4): 70-73.
[7] 李霞林, 郭 力, 冯一彬,等. 基于非线性干扰观测器的直流微电网母线电压控制[J]. 中国电机工程学报, 2016, 36(2): 350-359.
[8]卜祥伟, 吴晓燕, 陈永兴,等. 非线性干扰观测器的高超声速飞行器自适应反演控制[J]. 国防科技大学学报, 2014(5): 44-49.
[9] Johanastrom K,Canudas C D W.Revisiting the LuGre friction model[J].IEEE Control Systems Magazine,2008,28(6):101-114.
Backstepping Sliding Mode Controller Based on Non-linear Disturbance Observer for Flight Simulator Servo Systems
Chang Cheng1, Chang Yanan2, Ai Fei1
(1.699 Factory Military Agent’s Room, Rocket Force, Chinese People’s Liberation Army,Beijing 100039,China; 2.61660 Troops, Chinese People’s Liberation Army,Beijing 100039,China)
A method of backstepping sliding mode controller based on non-linear disturbance observer is proposed for the flight simulator servo systems considering the nonlinear friction, parameter uncertainty and torque fluctuation. In this method, the backstepping control is used to design virtual control desired speed, then nonlinear disturbance observer is used to observe the composite uncertain disturbance of the system. On this basis, an adaptive global sliding mode controller is designed for the system using nonlinear disturbance observer, which can achieve the robust tracking control of desired angle signal of the flight simulator servo systems. Lyapunov based analysis proves the asymptotically stable performance of the system, and the tracking errors can asymptotically converge to zeros. The influence of the nonlinear friction to the flight simulator servo systems is investigated using simulation, and the effects of the PD controller and the backstepping sliding mode controller are compared.
non-linear disturbance observer; backstepping sliding mode control; flight simulator servo systems; uncertain disturbance
2016-06-20;
2016-07-17。
常 诚(1990-),男,河南郑州人,硕士,主要从事导航制导与控制方向的研究。
1671-4598(2016)12-0067-04
10.16526/j.cnki.11-4762/tp.2016.12.019
V249
A

