基于极限学习机与规则推理的NPC三电平逆变器二级故障诊断方法

陈 丽，蔡红军

(1.河北工业大学 电磁场与电器可靠性省部共建重点实验室，天津 300130；2.中铁电气工业有限公司保定铁道变压器分公司，河北 保定 071051)

基于极限学习机与规则推理的NPC三电平逆变器二级故障诊断方法

陈 丽1，蔡红军2

(1.河北工业大学 电磁场与电器可靠性省部共建重点实验室，天津 300130；2.中铁电气工业有限公司保定铁道变压器分公司，河北 保定 071051)

针对NPC三电平逆变器主电路故障难以诊断问题，提出一种基于极限学习机、小波技术和规则推理的二级故障诊断方法;方法通过对比分析逆变器输出电压信号和电流信号在不同故障时差异性，确定了逆变器故障模式和可区分性;根据故障模式和可区分性，提出采用小波技术从输出电流中提取故障低频小波能量作为故障诊断特征和采用极限学习机进行故障电流信号的初级分类;对于根据电流信号的初级诊断不可区分的故障，提出采用逆变器桥臂输出电压信号特征和规则推理法进行故障二级精确诊断;该方法充分利用了输出电压和电流信号区分故障的特点，不仅能区分NPC三电平逆变器主电路单故障，还能同时区分多故障;诊断实验表明，所提方法故障诊断速度快，准确率高，鲁棒性强。

NPC三电平； 故障诊断； 极限学习机； 规则推理法； 小波分析

0 引言

二极管中点钳位型(neutral-point clamped，NPC)三电平逆变器因其谐波含量低，耐高压，开关应力小,无需变压器和动态均压电路等优点[1-2]而广泛应用于电力工业场合，如静止同步补偿器(STATCOM)、电力有源滤波器(APF)、高压大电机变频器及大功率装置等。但三电平NPC逆变器功率器件多，可靠性低。当电路发生故障时，将不可避免的造成经济损失，因此研究NPC功率管的故障诊断，对于提高设备可靠性、保证安全运行等都具有重要意义。

目前，NPC逆变器故障诊断已经取得了初步成果。文献[3]提出一种基于多神经网络的故障诊断方法，采用三电平逆变器的上、中、下桥臂电压作为测试信号，利用桥臂电压的多种谐波含量和特征，信号采集及处理信息量大，高维特征向量作为神经网络的输入使得网络结构复杂，运算量增加，延长了故障诊断时间。文献[4]应用电流轨迹法针对NPC逆变器单开关管故障进行诊断。文献[5]详细的阐述了NPC主电路各功率管在故障时的工作情况及典型特征，并总结了故障诊断规则。文献[6]详细分析三电平变换器开路时的工作情况和表现形式，提出PWM电压和电流极性的变化来判断功率管的故障及定位，该方法诊断速度快，可靠性高，但该方法并没有精确定位到某个器件，需要人工查找。

通过NPC逆变器运行机制，提出了一种基于极限学习机(extreme learning machine, ELM)与规则推理(rules inference, EI)的二级故障诊断新方法。首先分析了正常情况和各种故障情况时输出电流的差异，进而依据输出电流讨论了故障的可分性及分类。通过从输出电流中提取特征，设计了基于极限学习机与规则推理的二级故障诊断系统。根据电流特征，利用极限学习机完成初级诊断。若初级诊断结果为电流不可区分的故障类型，则需要进行二级诊断。二级诊断通过提取桥臂电压的低频小波能量为特征，采用规则推理机实现故障精确诊断。该方法在多数故障情况下只需采集输出电流进行初级诊断，具有采集信息少、处理量小、结构简单、诊断快速等优点。

1 开关管开路故障分析

NPC三电平逆变器主电路如图1所示，由两个直流分压电容C1=C2、两个钳位二极管、4个功率开关管和4个续流二极管构成[7-8]。

图1 NPC逆变器主电路

1.1 工作模式

以NPC逆变器A相输出正向电流(从逆变器流向负载)为例来分析工作情况：

模式1：t∈[t1,t2]当开通Sl、S2，关断S3、S4时，电流从P点流向主开关器件Sl、S2，输出端电位与P点相同，输出电压U=+Vdc/2 ，如图 2(a)所示。

模式2：t∈[t1,t2]当开通S2、S3，关断Sl、S4时，电流从O点依次流向钳位二极管Dl、S2，此时该相输出端电位与O点电位相同，输出电压U=0，如图 2(b)所示。

模式3：t∈[t2,t3] 当开通S3、S4，关断Sl、S2时，电流从N点流过与主开关管S3、S4反并联的续流二极管，输出端电压U=-Vdc/2 ，如图 2(c)所示。

模式4: t∈[t2,t3]基本与模式2相同，如图 2(d)所示。NPC电路在阻感负载下的输出电流与调制电压如图2(e)。

图2 工作模式与模式区间

由图2可见，当NPC变换器正常工作时，输出电流为正弦波；当NPC功率管开路故障时，输出电流出现流向出现了变化，会导致波形发生变化。下面以A相单管开路和两管同时开路为例分析输出电流的变化。

1.2 基于负载电流的故障可分性

NPC变换器故障可分为单管故障和双管故障。单管故障选S1开路和S2开路故障为例进行分析，其它故障可类似得到。电路正常、选S1开路和S2开路故障的电流波形分别如图3所示。由图2可见，当 S1故障时，正常模式1电流无法流经S1而直接进入模式2，会使正向输出电流大幅值衰减，电流波形如图3(b)；当S2故障时，模式1和2中均无法输出正向电流，直接经S3、S4输出反向电流，其电流波形如图3(c)。由此可见，开关管故障位置不同会引起电流衰减程度不同，上桥臂开关管S1故障时会使得正向电流大幅值衰减，S2位置故障会使得正向电流几乎衰减为0。

图3 正常和单个开关管故障时的电流波形

根据两管故障位置，两管故障可分为：1)上桥臂与下桥臂两管交叉故障，2)半桥臂故障(如上桥臂两管同时故障)。

两管交叉故障共计4种组合：S1和S3，S2和S3，S1和S4，S2和S4。当S1和S3故障时，S1故障导致正向电流减小，S3故障导致负向电流中断；当S2和S3故障时，正向和负向电流几乎变为0；故障电流波形如图4所示。其它两管交叉故障可类似分析。

图4 两个开关管同时发生故障时的电流波形图

比较图3和图4，单管故障和两管交叉故障时的输出电流波形均不同，因此可从负载电流中提取特征用于故障诊断。

半桥臂双故障只有两种组合，上桥臂故障和下桥臂故障。上桥臂故障，即当开关管S1和S2故障时，模式1和2均被破坏，故障电流与S2单独故障时相同，输出电流也相同；同理，下桥臂S3和S4故障输出电流波形同S3单故障相同。由此可得，半桥臂双故障与单故障无法区别，故把它们归为一类故障，称为负载电流不可区分故障类型。

综上可见，输出电流不能用于区分半桥臂双故障外，其他故障情况均可区分。

1.3 基于桥臂电压的故障可区分性

针对输出电流无法诊断半桥臂双故障，需采集新的测量信号，即输出电压信号。NPC电路工作在模式1时，若只有S2故障，电压Vuo(如图1)为Vdc/2；若S1、S2同时故障，电压Vuo为0。显然，桥臂电压Vuo在S2故障和S1、S2双故障时波形存在差异，电压Vdo波形相同，电压波形如图5所示。同样S3故障和S3、S4双故障时电压Vdo波形存在差异，而电压Vuo波形相同。由此可以看出，电压Vuo主要受上桥臂功率管的影响，而电压Vdo主要受下桥臂功率管的影响。为了使采集信息少，故障诊断时间缩短，这里采集Vud，由图5可见，输出电压可诊断半桥臂双故障。

图5 桥臂电压波形

为了减少采集数据量，此处只采集桥臂电压Vud为故障诊断信号，且桥臂电压信号不易受负载波动的影响，抗干扰能力强。

2 NPC逆变器二级故障诊断

2.1 基本原理

NPC逆变器二级故障诊断分为初级诊断和二次诊断，具体如图6所示。初级诊断以逆变器输出电流为诊断信号，以极限神经网络为分类器进行故障初次诊断；二次诊断以输出电压为诊断信号，针对电流难以区分故障以规则推理进行二次故障诊断。其中诊断特征提取、极限神经网络分类器和推理规则建立是故障诊断关键，下面分别介绍。

图6 二级故障诊断流程

2.2 特征提取

2.2.1 电流特征提取

采用电流均值表征电流极性，低频小波能量表征电流幅值，并进行归一化以消除负载波动对诊断的影响，将其值构造特征向量，以实现除电流不可区分的故障类型外其他故障模式的诊断定位。

将电流均值与低频能量归一化值构造特征向量，作为极限学习机分类器的输入以实现初级故障诊断。利用小波变换提取电流低频能量[9-10]与电流均值构成特征向量的具体步骤如下：

1)将NPC电路输出的各相电流进行3层小波分解，得到三相负载电流信号各层小波分解系数。

2)对小波分解系数进行重构，提取各频带的信号。低频信号是原始信号的逼近，可将三相低频能量作为特征向量。

典型的故障样本如表1。对于桥臂电压信号的低频小波能量提取同上步骤。

表1 典型故障样本

表2 负载输出电流、诊断电流及灵敏度

2.2.2 负载影响

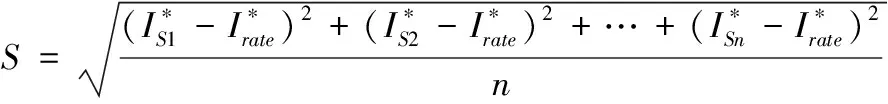
2.3 分类器设计

2.3.1 ELM故障分类器

ELM是为单隐含层神经网络(single hidden layer feed forward neural networks，SLFN)而提出的新型算法[12]，SLFN模型见图7。

图7 典型 SLFN 模型

对于N维样本(xj,tj)∈RN×Rn, L个隐含层节点和激励函数g(x)，则SLFN的输出可表示成:

(1)

这里:yj表示为第j个输出节点的输出值; βi为连接第i个隐含层节点和输出节点的权值矢量; ωi为连接训练样本x和第i个隐含层节点的权值矢量; bi为第i个隐含层节点的阈值;

上述还可矩阵表示为：

Hβ=T

(2)

H为隐含层输出矩阵, 矩阵H的第i列为对应输出样本x的第i个隐含层节点输出hi,hi=(g(ω1ix1+bi) … g(ωNixN+bi))T。

经证明如果激励函数g(x)无限可微, 则SLFN的隐含层节点参数ωi、bi无需反复调整[13-14]。当ωi、bi任意给定后，由Moore-Penrose广义逆定理求解唯一解H+，则β=H+T，H+指隐含层输出矩阵H的广义逆矩阵。

2.3.2 ELM分类算法

(3)

这里, ξi=[ξi1… ξin]是对应输入xi的输出训练误差；C是随机指定的正则化参数。

上述满足KKT条件,利用Lagrange函数转换为一个二次规划问题：

(4)

ELM分类算法使网络结构简单，整个过程一次完成，参数无需迭代，与BP神经网络相比，训练速度得到显著提高，避免了多次迭代和局部最小值。

2.3.3 规则推理机的设计

若ELM分类器诊断结果为电流不可区分故障类型时，需要规则推理法[15-16]精确定位故障器件。首先采集输出电压信号，对电压信号提取低频小波能量作为规则推理机的输入，将S2单独故障时小波能量作为参考值，通过桥臂电压小波能量与参考值进行比较，若在阈值内则输出0，表示S2单独故障，反之输出1，表示S1、S2同时故障，规则推理故障诊断原理如图8所示。

图8 规则推理故障诊断原理图

4 诊断实验

对三相电流提取特征向量，作为ELM的学习样本，极限学习机输入节点为6个，隐含层设置13个节点，传递函数采用Sigmoid函数，输出层采用单节点输出，ti=i,i=1,2…p表示p标签，对负载电流不可区分故障类型(如S2故障和S1、S2同时故障)取相同的标签，见表1。预测标签为输出值最接近的正整数值。在诊断实验中，NPC直流电源允许±5%波动，负荷可以在一定范围内增大或减小。诊断时直流电压分别为530V，525V/535V，负荷为(10+j5) /(9+j4.5)/(11+j5.5)kVA,诊断结果正确率达100%，部分初级故障诊断结果如表3。

表3 部分初级故障诊断结果

对于电流不可区分的故障类型的故障，采用规则推理法精确定位故障元件，选取在额定负载下S2单独故障时低频小波能量作为参考值，阈值为0.1×103，表4列出了对电流不可区分的故障类型的故障诊断，诊断结果表明该故障诊断方法可精确定位故障元件。

表4 规则推理法对电流不可区分的故障类型的故障诊断结果

本文引入BP神经网络与ELM的诊断结果进行对比，传递函数采用Sigmoid函数，训练方法采用反向传播算法。输出层设置4个节点。采用本文所提方法和传统BP神经网络分别对故障样本进行10次训练，根据诊断结果从训练时间、正确率的均值与方差3个角度去评价ELM算法的训练性能，如表5所示。

由表5可见，与BP神经网络诊断方法相比，极限学习机在训练速度、泛化能力和鲁棒性能3个方面得到了显著的提高。

表5 提出方法和BP神经网络对样本训练性能比较

5 结论

本文针对NPC开路故障的特点，提出的基于极限学习机与规则推理的二级故障诊断方法，能够实现对NPC三电平单管和两管同时故障的多模式故障诊断。较传统故障方法，有以下优点：

1)NPC电路故障在多数情况下为非电流不可区分的故障类型的故障，只需对三相输出电流提取电流均值和低频能量，只有在确定为负载电流不可区分故障类型时才对故障相桥臂电压提取特征向量，与传统方法中盲目对三相电流和电压提取各谐波含量作为特征向量相比，大大减少了信号的处理量，缩短了故障诊断时间。

2)将负载电流不可区分故障类型采用规则推理法进行故障定位，大大降低了极限学习机的分类要求，这就使得极限学习机的输入特征向量维数降低，同时也使得极限学习机的结构大大简化，运算量呈指数形式下降，故障诊断时间显著缩短。

3)ELM与传统BP神经网络相比，在采用相同的结构和学习样本时，由于ELM采用广义逆求解隐含层与输出层的权值，无需迭代，因此ELM学习速度快，正确率显著提高。

4)负载对故障诊断影响小，负载电流通过归一化处理及ELM的容错能力能消除了负载波动对故障诊断结果的影响，而桥臂电压基本不受负载波动的影响，故所提方法解决了传统方法中负载波动会对诊断结果造成影响的问题。

[1]NabaeA,TakahashiI,AkagiH.Anewneutral-point-clampedPWMinverter[J].IEEETransactionsonIndustryApplications，1981 (5): 518-523.

[2]RodriguezJ,BernetS,SteimerPK,etal.Asurveyonneutral-point-clampedinverters[J].IEEETransactionsonIndustrialElectronics， 2010, 57(7): 2219-2230.

[3] 陈丹江, 叶银忠. 基于多神经网络的三电平逆变器器件开路故障诊断方法[J]. 电工技术学报, 2013, 28(6): 120-126.

[4]SonHI,KimTJ,KangDW,etal.Faultdiagnosisandneutralpointvoltagecontrolwhenthe3-levelinverterfaultsoccur[A].PowerElectronicsSpecialistsConference,PESC04.IEEE35thAnnual[C].IEEE, 2004, 6: 4558-4563.

[5] 周京华, 刘辉臣, 姚兰亚,等. 三电平大功率变频器故障特征及诊断方法研究[J]. 电力电子技术, 2009, 43(6): 1-3.

[6] 汤清泉, 颜世超, 卢松升, 等. 三电平逆变器的功率管开路故障诊断[J]. 中国电机工程学报, 2008, 28(21): 26-32.

[7]NabaeA,TakahashiI,AkagiH.Anewneutral-point-clampedPWMinverter[J].IEEETransactionsonIndustryApplications, 1981 (5): 518-523.

[8] Rodriguez J, Lai J S, Peng F Z. Multilevel inverters: a survey of topologies, controls, and applications[J]. IEEE Transactions on Industrial Electronics, 2002, 49(4): 724-738.

[9] Camps O I, Robertson D C, Mayer J S. Wavelets and power system transients: feature detection and classification[A].The SPIE International Symposium on Optical Engineering in Aerospace Sensing[C]. 1994, 2242: 474-487.

[10] Mallat S G. A theory for multiresolution signal decomposition: the wavelet representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(7): 674-693.

[11] 彭玉华.小波变换与工程应用[M]. 北京:科学出版社,1999.

[12] Huang G B, Zhou H M, Ding X J, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2012, 42(2): 513-529.

[13] Huang G B, Zhu Q Y, Siew C K. Extreme learning machine: a new learning scheme of feedforward neural networks[A]. 2004 IEEE International Joint Conference on Neural Networks, Proceedings[C]. IEEE, 2004, 2: 985-990.

[14] Huang G B, Qin Y Z, Siew C K. Extreme learning machine: theory and applications[J]. Neurocomputing, 2006, 70(1): 489-501.

[15] Szczesny R, Kurzynski P, Piqueb H, et al. Knowledge-base system approach to power electronic systems fault diagnosis[A]. ISIE'96., Proceedings of the IEEE International Symposium on Industrial Electronics[C]. IEEE, 1996, 2: 1005-1010.

[16] Bose B K. Expert system, fuzzy logic, and neural network applications in power electronics and motion control[J]. Proceedings of the IEEE, 1994, 82(8): 1303-1323.

A Method of Two Layers Fault Diagnosis Based on ELM and RI Theories for NPC Inverter

Chen Li1, Cai Hongjun2

(1.Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability, Hebei University of Technology, Tianjin 300130, China; 2.Baoding Railway Transformer Branch Company of China Railway Electric Industries Co.Ltd, Baoding 071051, China)

Aiming to the difficulty of faults diagnosis of power devices in NPC converters, a new fault diagnosis method based on extreme learning machine(ELM), wavelet techniques and rules inference (RI) theories for NPC inverter is proposed in this paper. By comparing the waveforms of output current and output voltage of the NPC inverter on different faults, the fault modes and its distinguishability with current output and output voltage of the NPC inverter are obtained in this paper. According to the distinguishability and fault modes, the primary diagnosis method is proposed by using the low frequency features extracted from output current with wavelet technique and by using the extreme learning machine for primary classification. If the primary result is the current undistinguishable fault, the rule inference based on information of bridge voltage is proposed to accurately locate the fault components, which is the second level diagnosis. The proposed method takes full distinguishable advantages of output current and output voltage of the NPC inverter, and can not only diagnosis and detect the single fault, but also the multi-fault patterns. The examples shows that the method is effective, fast and robust.

NPC three level; fault diagnosis; extreme learning machine;rules inference;wavelet analysis

2016-05-25；

2016-07-29。

国家自然科学基金(51477040)。

陈 丽(1980-)，女，安徽萧县人，在读博士，讲师，主要从事电力电子技术方向的研究。

1671-4598(2016)12-0006-05

10.16526/j.cnki.11-4762/tp.2016.12.003

TM464

A