关于数列通项公式求解的分类讨论

◇ 江苏 季明峰

关于数列通项公式求解的分类讨论

◇ 江苏 季明峰

数列问题在高考中是C级要求,数列通项公式的求解是数列的重要知识点,而根据问题情境以及所给题设的不同,有累加法、累乘法、降项作差法、待定系数法等不同的处理方式,因此,需要对数列通项公式的求解进行归类讨论.

1 一道调研试题引发的思考

数列通项的求解在高中数学里占有十分重要的地位,它存在多种处理方式,2016年南通市高三第一次调研试卷第20题的通项求解,将笔者的思维引向了通项求解的归纳与整理上.

例若数列{an}中存在3项按照一定次序排列能构成等比数列,称数列{an}为等比源数列,数列{an}中a1＝2,an＋1＝2an－1.

(1)求数列{an}的通项公式.

(2)判断数列{an}是否为等比源数列.

解析

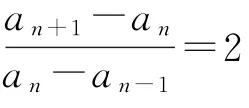
点评

这种问题是典型的降项作差法,其题设条件如an＋1＝kan＋b.但实际情境中学生遇到的题设并不仅限于这种类型,表达形式还有诸如an＋1＝an＋f(n)、an＋1＝an·f(n)(an≠0)、an＋1＝kan＋b以及an＋1＝kan＋ban－1(an＋1＝kan＋f(n))等,每种形式会对应着一种处理方式,需要归类解析.

2 常见形式的数列通项求解归纳

1)型如an＋1＝an＋f(n)用累加法.

观察an＋1＝an＋f(n)的表达式,不难发现数列的后一项与前一项之差f(n)是关于n的一个离散型函数,其自变量与前一项an的下标相同,故有an＋1－an＝f(n),an－an－1＝f(n－1),an－1－an－2＝f(n－2),…,a2－a1＝f(1).这与等差数列通项公式推导过程相似,由此得到启示,型如an＋1＝an＋f(n)的问题用累加法得an＝f(n－1)＋f(n－2)＋…＋f(1)＋a1.需要说明的是利用累加法求得通项公式时应当验证n＝1时,a1与所求通项公式是否相匹配.

2)型如an＋1＝an·f(n)(an≠0)用累乘法.

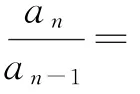
3)型如an＋1＝kan＋b用降项作差法.

例1就属于这种类型.由于数列的后一项总等于前一项加上一个常数,因此通过降项可得到an和an－1的关系an＝kan－1＋b.将2式作差,不难发现

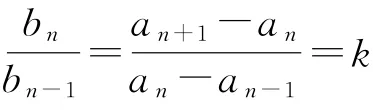
4)型如an＋1＝kan＋ban－1或an＋1＝kan＋f(n)用待定系数法.

当问题情境所给题设条件为an＋1＝kan＋ban－1或an＋1＝kan＋f(n)时,由于降项相减的法则,只能适用于所加项为常数的情境,而此时等式右侧所加项是一个关于n的表达式,降项相减不能适用,但可以从中得到破题的启示.以an＋1＝kan＋ban－1为例,给等式左、右侧各配上一个m·an,则可得an＋1＋m·an＝(k＋m)an＋ban－1,提取(k＋m)后得,则可得到的值为常数t(t＝k＋m),从而将原的问题转化成型如an＋1＋m·an＝t(an＋man－1)的问题,如此可用等比数列的方式做后续处理.

(作者单位:江苏省大丰市南阳中学(大丰港校区))