三角函数最值问题的常见解法
杨爱东
(江苏省盐城市田家炳中学,224001)
三角函数最值问题的常见解法
杨爱东
(江苏省盐城市田家炳中学,224001)
纵观江苏近几年高考试卷不难发现,在对三角函数内容进行考查时,出现了一种重要的题型——求三角函数的最值.该题型灵活多变,对于培养学生的综合应用能力有着重要意义.本文结合具体案例简要阐述三角函数最值问题的几种常见解法.
一、利用配方法
配方法是高中数学解题中的基本方法,也是解决三角函数最值问题的重要依据之一.配方法是指将一个二次多项式通过变形配成一个一次多项式平方与一个常数和的形式的一种方法,然后利用二次函数的性质,从而达到求取最值的目的.配方法在三角函数求最值中应用较多,其仅适用于只含有正弦函数或余弦函数的三角函数求最值问题.
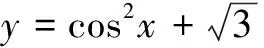
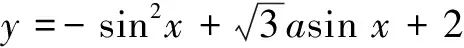
配方后得
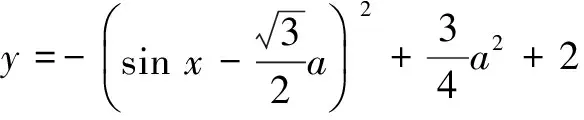
利用二次函数的性质,即可知当
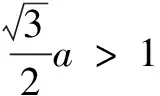
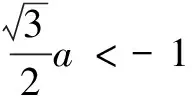
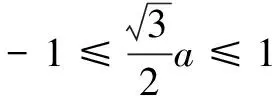
从而解决问题.
二、利用辅助角
利用辅助角也是三角函数求最值常用的方法之一.三角函数公式繁多,题型灵活,大部分求最值问题往往不可直接得出,而是需要借助于一些三角函数的公式进行变形,通过引入辅助角达到解决问题的目的.
分析 乍看好像与上面的题目相似,但仔细分析又会发现,无法将这个函数转化为一个只含有正弦或余弦的函数,显然用配方法无法解决.通过观察发现,函数中cos2x、sin2x都与cos 2x有着一定的联系,于是,可将2cos2x-1=cos 2x,1-2sin2x=cos 2x经过变形后代入原函数,即可得到
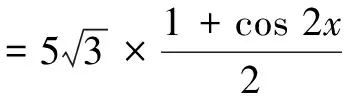
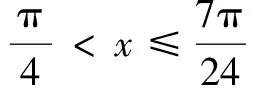
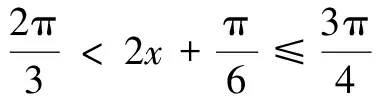
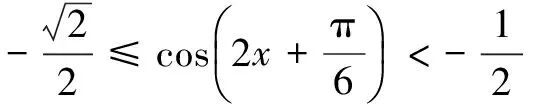
三、利用三角函数的有界性
三角函数是一种特殊的函数,有界性是正、余弦函数一个最重要的特征,这也就给求三角函数最值问题提供了一个重要的方法.利用三角函数的有界性求函数的最值主要解决的是分子分母同名、同角的题目,通过变形化为分式形式,再利用有界性去解决.
分析 这道题无法用配方法去解决,也无法通过降次利用辅助角去解决.但通过发现,此题最大的特点是分子、分母中只含有正弦函数,于是可将函数关系通过恒等变形,得
(y+1)sin x=2y+1.
由于y≠-1,可得
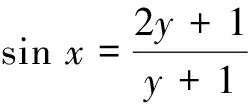
根据正弦函数|sin x|≤1,可得
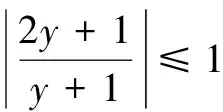
这种利用正、余弦函数的有界性求三角函数最值的方法为高中数学中其它求最值问题提供了借鉴.
总之,三角函数求最值问题是高中数学的重要内容之一,是高考中经常涉及到的问题,正确研究此类题目的解题方法有着重要的意义.利用配方法、利用辅助角、利用三角函数的有界性求三角函最值问题是求三角函数最值最基本的几种方法.在教学过程中教师一定要加强方法指导,提高学生的解题能力,为学生在后来的学习中打下坚实的基础.

