FTN系统中基于矩阵分解的新型干扰消除算法*
张广娜,郭明喜,沈越泓
(解放军理工大学 通信工程学院,江苏 南京 210007)
FTN系统中基于矩阵分解的新型干扰消除算法*
张广娜,郭明喜,沈越泓
(解放军理工大学 通信工程学院,江苏 南京 210007)
1975年,Mazo首次提出了超奈奎斯特(Faster-than-Nyquist)码元速率传输系统。相比于传统的Nyquist传输体系,该系统可以有效提高系统的带宽有效性和传输速率,因此接收端不可避免地引入了无限长的码间串扰(Inter-symbol Interference),增加了接收复杂度。因此,需在接收端进行干扰消除。基于矩阵QR分解的部分判决反馈均衡(Partial Decision Feedback Equalization)可以作为FTN系统中有效的干扰消除和信号检测算法,但该算法的计算复杂度较高。于是,提出了一种FTN传输系统中基于矩阵分解的新型干扰消除算法。仿真结果表明,该算法的误码率性能优于PDFE,且由于避免了QR分解,使其计算复杂度大大降低。
超奈奎斯特码元速率传输;干扰消除;计算复杂度;部分判决反馈均衡;新型算法
0 引 言
相比于传统的正交调制体系,超奈奎斯特(Faster-than-Nyquist)码元速率传输体系是未来前景广阔的通信系统,可以有效提高系统的传输速率和带宽有效性。1975年,Mazo首次提出了FTN理论[1]。理论证明,在相同带宽﹑相同能量且不损失性能的情况下,FTN系统可以传输更多的数据符号[2]。但是,由于较高的接收复杂度,FTN系统在当时并未引起人们较多的关注。
近年来,FTN系统日渐受到人们的青睐。2003年,Liveris和Georghiades[3]仿真分析了二进制FTN信号系统中错误事件结构和采用根升余弦脉冲时的控制编码理论。Rusek和Anderson[4]于2006年研究了FTN系统采用根升余弦脉冲时信息速率的最大值和最小值,并证明“由于过剩带宽导致FTN系统提供更高的信息速率”。2008年,人们研究了非二进制FTN及其最小欧氏距离[5]。然而,由于FTN系统提高了通信系统的传输速率,接收端不可避免地引入了无限长的码间串扰。因此,消除码间串扰带来的计算复杂度成为阻碍FTN信号应用的重要因素。目前,人们已经提出了一些FTN系统接收端的解调算法。其中,Forney和Hayes分别提出了最大似然序列估计MLSE(Maximum Likelihood Sequence Estimation)[6]和维特比算法VA(Viterbi Algorithm)[7]。但是,由于FTN系统引入的码间串扰长度无限长,导致MLSE和VA的复杂度太高而难以实现。低复杂度的BCJR算法也被用于FTN系统中的干扰消除[8-9],但网格解码的计算复杂度仍然较高。文献[10]提出了一种基于矩阵分解的干扰消除算法,仿真结果表明,部分判决反馈均衡的误码率性能优于维特比算法,但由于矩阵的QR分解导致该算法的计算复杂度高。
基于上述研究情况,本文提出一种FTN系统中基于矩阵分解的新型干扰消除算法。仿真结果表明,该算法的误码率性能优于PDFE,同时由于不采用QR分解,大大降低了其复杂度。文章结构如下:第一部分给出FTN系统的传输模型和干扰矩阵;第二部分介绍部分判决反馈均衡;本文提出的干扰消除算法在第三部分进行介绍;第四部分给出各算法误码率性能及比较结果;最后归纳全文。
1 系统模型
普通二进制线性调制信号的基带形式为:

其中an为等概独立同分布的实信号,g(t)为单位能量调制脉冲,其符号周期为T秒[11]。对于FTN信号,g(t)为非正交调制脉冲,且符号周期为τT,τ为时间加速因子。
图1给出了FTN信号的信道模型以及发送接收端。随着加速因子的减小,脉冲发送速率增加,且脉冲能量成比例减小。因此,在发送端用归一化所有脉冲,即,从而降低脉冲能量且保持发送端能量不变。

图1 FTN系统传输模型
信号经过加性高斯白噪声信道后,接收信号r(t)为:

其中w(t)为方差为σ2的实的白噪声,接收信号经过匹配滤波器并每τT秒采样得到序列:

式(3)的等价离散时间模型可表示为:

其中,矩阵w表示有色高斯噪声,其协方差矩阵为σ2G;矩阵G表示FTN系统中的码间串扰,为Toeplitz﹑Gram矩阵。当码间串扰为零时,该矩阵为对角阵。由于FTN引入的码间串扰无限长,干扰矩阵G的维度无限大。但码间串扰主要是由临近的几个符号决定,故取干扰矩阵维度为N×N。对于根升余弦调制脉冲g(t),其干扰矩阵可表示为:
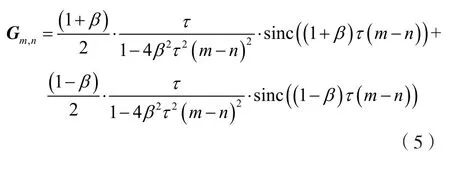
其中,β为根升余弦脉冲的滚降系数[12]。
2 FTN系统中的部分判决反馈均衡(PDFE)
干扰消除和信号检测最简单的方法为迫零算法,即接收信号向量Y左乘干扰矩阵G的Moore-Penrose逆。该方法因左乘逆矩阵导致噪声幅度增加,使得误码率性能下降,因此未能得到广泛应用。
PDFE为FTN通信系统中另一简便干扰消除算法。该算法基于干扰矩阵的QR分解,且每次检测c(c<N)个符号,重复检测[N/c]次,其中[x]表示取不超过x的最大整数。
PDFE的主要步骤如下。
(1)选取维度为c×c的分块矩阵
选取的第一部分分块矩阵为:

(2)QR分解
对分块矩阵G(1)做QR分解,即G(1)=Q(1)R(1)。Q(1)是酉矩阵,满足Q(1)HQ(1)=I,(·)H表示对矩阵做共轭转置,R(1)为上三角矩阵。
将Y(1)=G(1)a+w(1)左乘Q(1)H,得到:
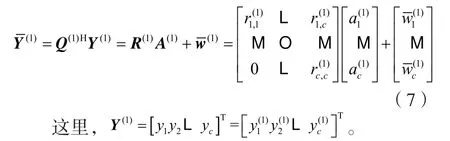
(3)硬判决和干扰消除
硬判决得到的c个符号为:
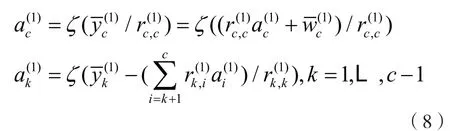
其中,m=ζ(n)表示对m与n之间的最小欧氏距离取整。因此,检测得到第一部分c个发送符号为:
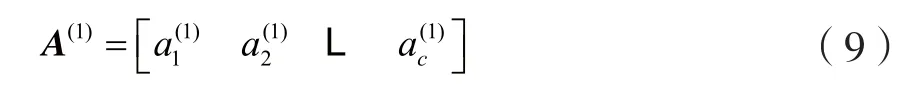
(4)检测剩余发送符号
在检测第二部分c个符号前,首先要进行前向干扰消除:
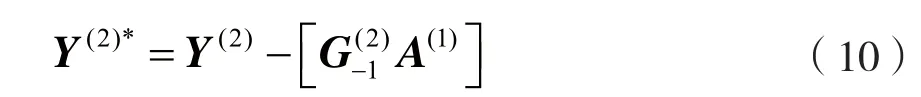
其中:


第二部分c×c分块干扰矩阵可表示为:
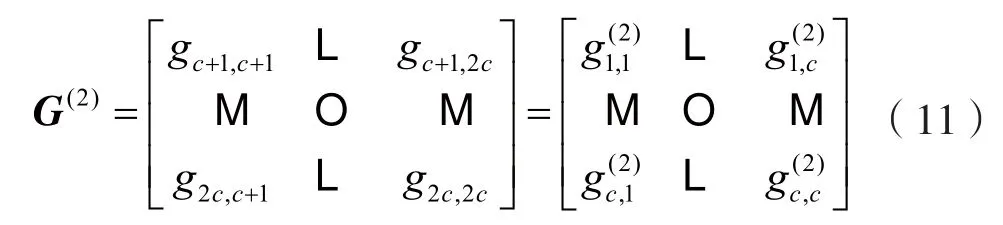
重复步骤(2)和步骤(3),检测得到第二部分c个发送符号为:

依次重复上述步骤[N/c]次,即可检测出所有发送符号。
3 新型干扰消除算法

本文提出了一种误码率性能优于PDFE的新型干扰消除算法,该算法避免了采用矩阵的QR分解,使得其计算复杂度远低于PDFE。
3.1 计算步骤
3.1.1 选取维度为c×c的分块矩阵
此时,选取的分块矩阵和式(6)相同,且第一部分c个接收信号为:
3.1.2 将分块干扰矩阵下三角元素置零
将分块干扰矩阵下三角元素置零后,式(4)的等效离散时间模型为:
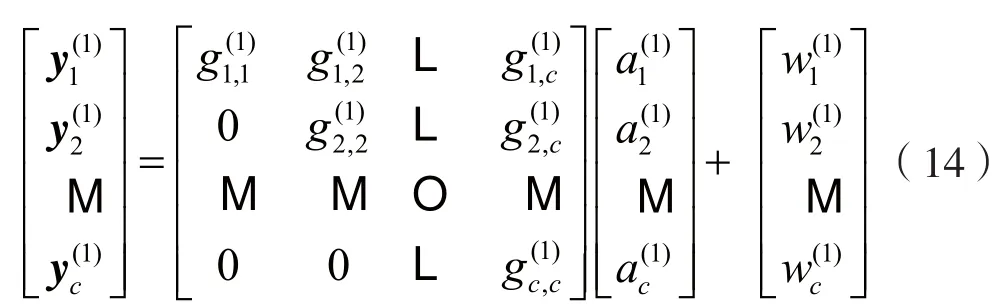
从式(14)的最后一行做硬判决,得到第一部分c个符号检测为:

同时,定义:
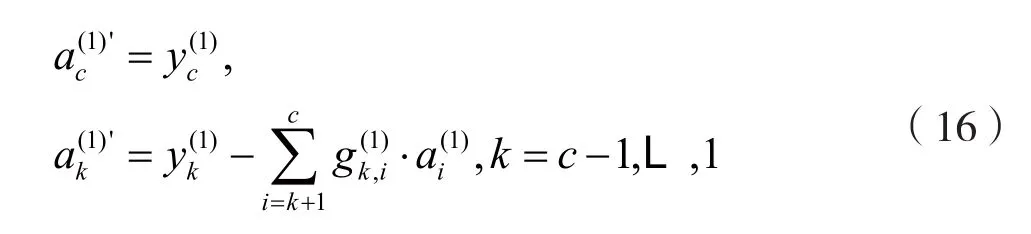
3.1.3 将分块干扰矩阵上三角元素置零
此时,式(4)的等效离散时间模型为:
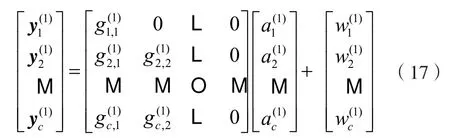
从式(17)的第一行做硬判决,得到第一部分c个符号检测为:
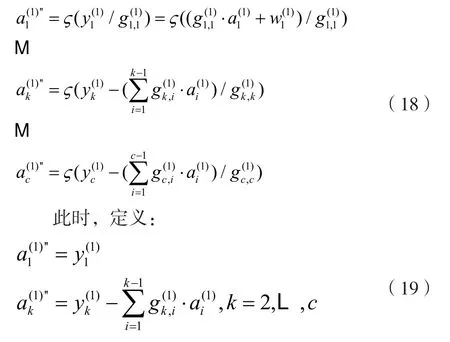
3.1.4 检测第一部分c个发送信号
分别将分块干扰矩阵G(1)的上下三角元素置零后,得到两个序列a(1)'和a(1)''。章节3.1.2和章节3.1.3中的干扰,分别来自于后半部分符号和前半部分符号,即。因此,第一部分信号检测为:
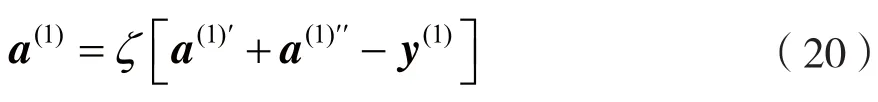
需要指出的是,章节3.1.2和章节3.1.3所涉及的步骤是等价的,即也可以先将分块干扰矩阵上三角元素置零,后将下三角元素置零。
3.1.5 检测其他发送符号
为检测第二部分发送信号,仍需采用式(10)的方法做前向干扰消除。其中,a(1)即为式(9)中的A(1)﹑Y(2)和G(2)-1与PDFE算法中步骤(4)的取值相同。选取第二部分c×c分块干扰矩阵,该矩阵等同于式(11),此时检测得到:
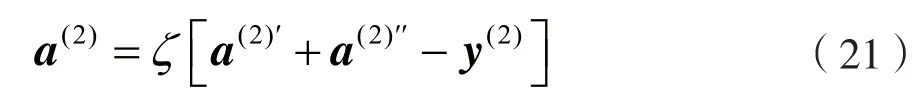
3.2 计算复杂度比较
为简化运算,我只考虑复乘和干扰矩阵G的分块大小。表1给出了PDFE和新型干扰消除算法的计算复杂度。

表1 PDFE和新型算法复杂度比较
其中,对于PDFE,分块矩阵QR分解的复杂度正比于O(c3),为复乘的复杂度,c2为前向干扰消除的复杂度。对于新型干扰消除算法,由于其不采用QR分解,且由表1中复杂度的比较,明显可知,该算法的复杂度远低于PDFE的复杂度。当考虑干扰矩阵G中的零元素时,该算法的复杂度将进一步降低。
4 仿真结果
通过仿真,分别给出了二进制FTN通信系统中新型干扰消除算法和PDFE的误码率性能。仿真中采用滚降系数β=0.2的根升余弦调制脉冲。
图2给出了加速因子τ=0.9时两种干扰消除算法的误码率性能。和理论结果相同,新型干扰消除算法的误码率性能优于PDFE,且随着分块干扰矩阵大小c的减小,两种算法的误码率性能均变差。但是,只要两种算法c取值相同,新型算法仍较PDFE的误码率性能佳。此外,从图中可知,随着c的减小,新型算法性能变差的比PDFE要慢。

图2 τ=0.9时两种算法误码率性能比较
图3给出了加速因子τ取不同值时两种算法的误码率性能。由图3可得,τ值越小,两种算法的性能越差,但仍满足图2分析得到的新型算法性能优于PDFE的结论。因此,为得到较高的误码率性能,τ的取值不能太小。
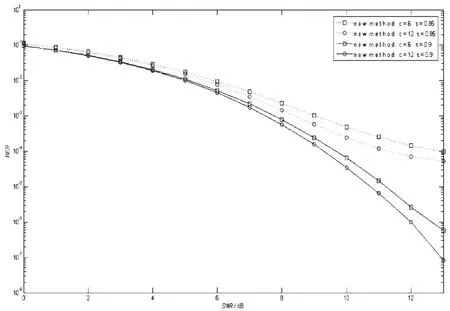
图3 τ=0.9和τ=0.85时新型干扰消除算法误码率性能比较
5 结 语
相比于传统的Nyquist传输体系,FTN传输系统可以有效提高系统的带宽有效性和传输速率,但同时接收端不可避免地引入了无限长的码间串扰,大大提高了接收复杂度。基于矩阵QR分解的PDFE算法能够有效解决这一问题,但其计算复杂度较高。因此,本文提出了FTN传输系统中一种新型的干扰消除算法,以进行有效的干扰消除和信号检测。通过仿真验证,该算法的误码率性能优于PDFE,且由于避免了QR分解,大大降低了计算复杂度。因此,该算法更适用于FTN通信系统。
[1] Mazo J E.Faster-than-Nyquist Signaling[J].Bell Syst. Tech. J.,1975,54(10):1451-1462.
[2] Chung Le,Malte Schellmann,Martin Fuhrwerk,et al.On the Benefits of Faster-than-Nyquist Signaling[C].In 2014 International Conference on Advanced Technologies for Communications,2014:208.
[3] Liveris A,Georghiades C.Exp loiting Faster-than-Nyquist Signaling[J].IEEE Transactions on Communicati ons,2003,51(09):1502-1511.
[4] Rusek F,Anderson J.Cth04-1:On Information Rates for Faster-than-Nyquist Signaling[C].IEEE Global Telecommunications Conference GLOBECOM,2006:1-5.
[5] Rusek F,Anderson J.Non Binary and Precoded Fasterthan-Nyquist Signaling[J].IEEE Transactions on Communicatio ns,2008,56(05):808-817.
[6] Forney G D.Maximum-likelihood Sequence Estimation of Digital Sequences in the Presence of Intersymbol Interference[J].IEEE Transaction Information Theory,1972,IT-18(05):363-378.
[7] Hayes J F.The Viterbi AlgorithMapplied to Digital Data Transmission[J].IEEE Communication Magazine, 2002,40(05):26-32.
[8] Anderson J B,Prlja A,Rusek F.New Reduced State Space BCJR A lgorithms for ISI Channel[C].ISIT 2009,2009:889-893.
[9] Prlja A,Anderson J B.Reduced-complexity Receivers for Strongly Narrowband Inter-sysmbol Interference Introduced by Faster-than-Nyquist Signaling[J].IEEE Transaction Communication,2012,60(09):2591-2601.
[10] Baek M S,Hur N H,Lim H.Novel Interference Cancellation Technique based on Matrix Computation for FTN Communication System[C].IEEE Military Communications Conference,2014:830-834.
[11] Anderson J B,Fredrik R,Viktor O.Faster-than-Nyquist Signaling[J].Proceedings of the IEEE,2013,101(08):1817-1830.
[12] Ringh E.Low Complexity Algorithm for Faster-than-Nyquist Signaling:Using Coding to Avoid an NP-hard Problem[D].Sweden:Royal Institute of Technology,2013.
A Novel Interference Cancellation Algorithm based on Matrix Decom position for FTN Signaling
ZHANG Guang-na, GUO Ming-xi, SHEN Yue-hong
(College of Communication Engineering, PLAUST, Nanjing Jiangsu 210007, China)
FTN(Faster-than-Nyquist) signaling, originally proposed by Mazo in 1975, and compared with traditional Nyquist system, could effectively improve the bandwidth efficiency and transmission rate of the communication system. Thus the inter-symbol interference is unavoidably introduced in the receiver, thus resulting in the complexity of the receiver. For this reason, it is necessary carry out interference cancellation in the receiver. PDFE(Partial Decision Feedback Equalization) based on QR decomposition is proposed as an efficient interference cancellation and signal detection algorithm for FTN-based communication system, and however, its computational complexity is very high. Thus a novel interference cancellation technique based on matrix decomposition is proposed to further improve the detection performance. Simulation results indicate that this novel method can perform better than PDFE, and its complexity is very low for absence of QR decomposition.
FTN(Faster-than-Nyquist) signaling; interference cancellation; computing complexity; PDFE; novel method

TN911
A
1002-0802(2016)-11-1433-05
10.3969/j.issn.1002-0802.2016.11.004
张广娜(1991—),女,硕士,主要研究方向为无线通信﹑超奈奎斯特速率传输等;
郭明喜(1978—),男,博士,讲师,主要研究方向为高速无线通信﹑MIMO和协同通信技术等;
沈越泓(1959—),男,博士,教授,主要研究方向为无线通信信号处理﹑高速数字调制技术﹑移动通信等。
2016-07-13;
2016-10-15 Received date:2016-07-13;Revised date:2016-10-15
国家自然科学基金资助项目(No.61301157)
Foundation Item:National Natural Science Foundation of China(No.61301157)

