基于DV-HOP的改进定位算法*
孟雯雯,赵建平,王 蒙,杨恒耀,张 浩
(曲阜师范大学 物理工程学院,山东 曲阜 273165)
基于DV-HOP的改进定位算法*
孟雯雯,赵建平,王 蒙,杨恒耀,张 浩
(曲阜师范大学 物理工程学院,山东 曲阜 273165)
节点定位技术是无线传感器网络的关键技术之一。基于双通信半径的DV-Hop定位算法,比传统DV-Hop算法大大提高了定位精度,但是还可以进一步改进。在双通信半径定位算法基础上,用跳数值变换概念改进锚节点计算平均每一跳距离的公式,并结合平均每跳距离进行加权处理。MATALB仿真实验证明,提出的基于双通信半径的跳数变换加权DV-Hop算法能提高基于双通信半径算法的定位精度,且不会增加节点的硬件成本。
无线传感器网络;节点定位;双通信半径DV-Hop;加权DV-HOP
0 引 言
无线传感器网络(Wireless Sensor Network,WSN)有大量微型﹑低成本的节点,在无人值守的应用环境中,节点一般由飞机等随机抛撒[1]。在无线传感器网络定位技术中,节点分两类:锚节点和未知节点。锚节点可以知道自己位置信息,但是成本比未知节点高,在网络中一般占少数。未知节点靠锚节点计算自身的位置信息,成本低,占网络中节点的大多数。网络中每个节点都需要知道自身位置,否则采集的信息毫无意义。定位技术有多种,其中无需测距定位算法因成本低﹑定位过程简单而得到了广泛应用[2]。在精度要求不是过高的定位应用中,DV-Hop算法是应用较为广泛的无需测距定位算法之一。
DV-Hop算法[3-6]只是用节点间广播的信息和跳数值计算坐标,误差很大。影响节点定位精度大的原因很多,如通信半径﹑锚节点平均每一跳距离﹑未知节点校正值的选取﹑锚节点部署方式等。许多文献为了提高定位精度,不断改进算法。本文结合文献[6]提出的基于多通信半径的DV-Hop改进算法,在求锚节点平均每一跳距离﹑未知节点校正值的选取上进一步改进算法,提出一种基于多通信半径最佳指数值下多跳数变换加权的DV-Hop算法。最后,通过仿真实验验证了算法的精度和稳定性。
1 基础概述
1.1 DV-Hop定位算法
DV-Hop定位算法是由美国罗格斯大学(Rutgers University)Dragos Niculescu等人提出的6种分布式定位算法之一[2]。
DV-Hop定位算法只是利用节点间的传输跳数值信息和锚节点的坐标值进行未知节点的坐标计算。假设网络中所有节点都可以进行双通信,且通信过程无障碍,每个节点都有自己的通信范围即通信半径,自带GPS导航设备的锚节点有n个。
DV-Hop算法步骤[3-6]如下:
第一步:锚节点向网络广播信息,包括自身位置信息﹑初始跳数值﹑节点编号等。路由方式为泛洪方式。设定一个较大的跳数值阈值,转播过程中如果跳数值超过阈值则转发停止。接收节点接到信息后,比较接收跳数值的大小。如果比自己保留的跳数值大,则抛弃信息;如果较小,则保留信息,并将跳数值加1后,转发出去。
第二步:锚节点根据第一步得知的其他锚节点的位置信息等,计算自己的平均每一跳距离:
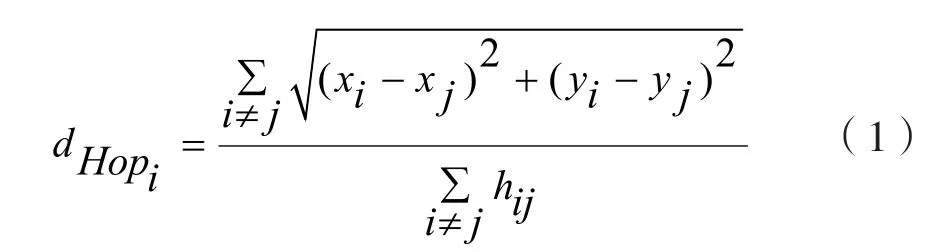
其中,锚节点i到其他锚节点的平均每一跳距离是dHopi,锚节点i﹑j间的最小跳数是hij。
第三步:锚节点再次向网络广播信息,包括自己的平均每一跳距离信息﹑节点编号。未知节点按照就近原则只接收一个锚节点的信息,并将其作为自己计算平均每一跳距离时的校正值。假设未知节点l的校正值为dHopp(即锚节点p为向该未知节点第一个送达信息),未知节点l与锚节点j间的跳数为hlj,则未知节点估算自己与其他锚节点间的距离为:

第四步:未知节点得到所有锚节点间的估算距离后,用三边测量法﹑极大似然法等计算自身坐标。假设未知节点坐标(x,y),未知节点与锚节点i间的估算距离di,则极大似然估计法如下:

算法的性能指标用定位精度判定。定位精度值越小,定位精度越高,如式(8):
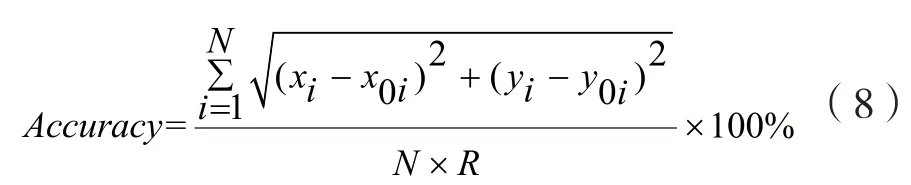
其中,网络中节点个数为N,节点通信半径为R,节点i的真实坐标与估算坐标则分别为(x0i, y0i)﹑(xi,yi)。
1.2 DV-HOP算法存在的不足
第一,利用传统DV-HOP算法,每个节点要接收和转发所有锚节点的数据包结构。这些节点处于活动状态,需要较长时间等待数据包,导致网络中的通信开销和能量消耗随之增加。
第二,锚节点所占的比例不同,平均跳段距离也就不同。比例越高,平均跳段距离越精确。当比例增加到一定程度时,距离保持稳定。但是,当锚节点所占比例过高时,则将增加所需费用。
第三,只是利用锚节点坐标信息和信息传输的跳数值定位,节点真实坐标与定位坐标之间误差很大。如图1所示,网络中分布着A﹑B﹑C三个锚节点,其他为未知节点。锚节点B的平均每一跳距离为,而计算的锚节点B的平均每跳距离要小于实际平均每跳距离,误差较大。此外,锚节点B到锚节点A﹑C的每一跳距离长短不一样,每两跳段间都有角度(三个锚节点不共线),所以用直线距离代替折段距离,求得校正值,误差很大。未知节点用校正值乘以最小跳数值估算与锚节点间的距离,导致较大的估算距离误差,最终影响定位结果的精确度。
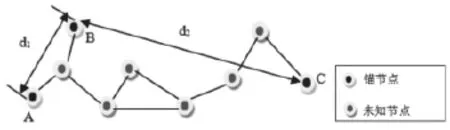
图1 网络节点分布
2 改进算法
2.1 改进锚节点每一条距离公式
文献[11]利用最小均方差准则,锚节点平均每一跳距离满足:
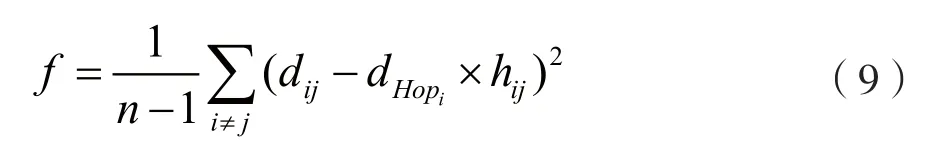
对函数f求关于dHopi的偏导并取零,得到最小均方误差下的平均每跳距离公式:

文献[12]用式(10)求锚节点平均每一跳距离,然后未知节点接收所有锚节点的平均每一跳距离。计算与锚节点间估算距离时,求到哪个节点的距离用它自己的平均每一跳距离,即求未知节点i与锚节点j的估算距离为:
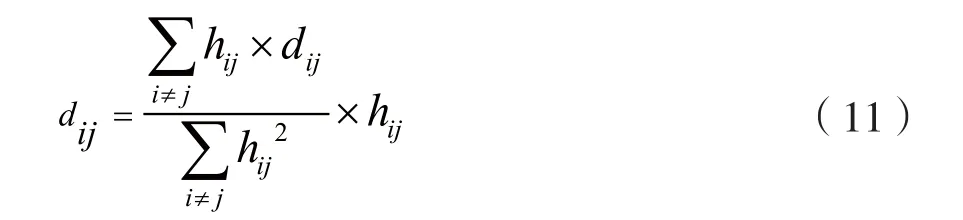
文献[4]改进式(10),提出最佳指数值概念,在最佳值下求锚节点平均每一跳距离。经过多次仿真发现,指数在取非2即取1.9~2.0间的数时,能提高定位精度,公式如下:
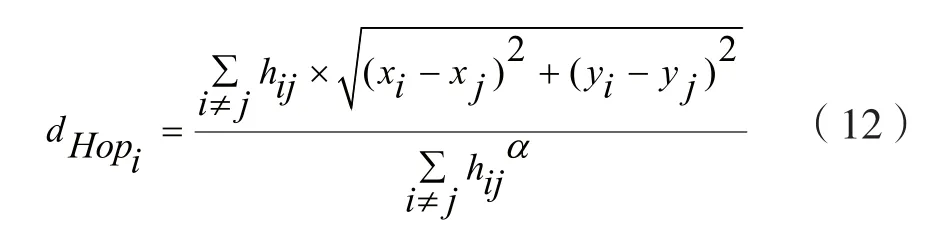
未知节点只接收离自己最近的锚节点发过来的平均每一跳距离信息。文献[6]将最佳指数的基应用到双通信半径中,提高了精度。文献[5]及文献[6]在给定节点每跳距离赋值时,都默认节点分布在以使用的锚节点为圆心,以R/2或R为半径的圆上,在节点随机分布的环境中,这种情况几乎不可能出现。鉴于此,本文就跳数变换给予。下文给出了求出最佳跳数值的具体方法。
2.2 改进未知节点选择校正值的方法
在未知节点选择和计算校正值时,文献[7]提出改进未知节点选择校正值的方法。求未知节点i校正值时,首先将锚节点p通过式(10)求得的平均每一跳距离乘以一个加权系数XSip。这个系数能体现未知节点i与锚节点p间的跳数值大小:

将所有锚节点乘以加权系数的平均每一跳距离累加,并将累加值作为该未知节点的校正值JZi:

最后,将未知节点i的校正值乘以与其他锚节点间的跳数值,求得该未知节点与其他锚节点间的估算距离:

2.3 改进节点间通信半径的方法
为了得到更精确的跳数值,文献[5]提出在计算平均每一跳距离时,提出可以考虑锚节点用多个通信半径的方法。以2通信半径为例,如图2所示。D﹑E﹑F为锚节点,a﹑b﹑c﹑d﹑e为未知节点,通信半径为R。锚节点D与未知节点a﹑b的距离分别为R﹑0.5R,锚节点E与未知节点b﹑c的距离都为0.5R。如果用一般的DV-Hop算法,锚节点D向未知节点a﹑b发送信息时,跳数值都加1;锚节点E向未知节点b﹑c发信息时,跳数值是1。假如锚节点有两个通信半径,分别为R﹑R/2,则当使用R/2通信半径时,节点D与b间的跳数值可以为0.5,节点E与b﹑c间跳数值可以为0.5。可见,这样基于2通信半径的DV-Hop算法得到的跳数值很精确。

图2 网络分布
但是,多通信半径算法也存在不足。在第二次及以后的泛洪中,若发送节点为未知节点,接收节点为锚节点,则未知节点到其一跳范围内的锚节点间的跳数值记为1。如果未知节点到锚节点的距离在R/2范围内,跳数值仍记1,则导致计算平均每一跳距离时的误差很大。如图2所示,未知节点d﹑e向锚节点F发送信息,若按文献[5]算法,则跳数值都加1,而未知节点d﹑e与锚节点F间距离分别为R﹑R/2。所以,文献[5]算法只是将第一次泛洪时锚节点到未知节点的跳数值记为0.5或1,没有考虑转播过程中的精化跳数值。
因此,本文在双通信半径基础上将跳数值精化,求出阈值内最佳跳数值u。仿真结果表明,本文方案极大提高了定位精度。
3 MATLAB实验
3.1 仿真环境验证
在边长为100 m的正方形区域分布109个节点,其中9个锚节点。节点分布环境,如图3所示。
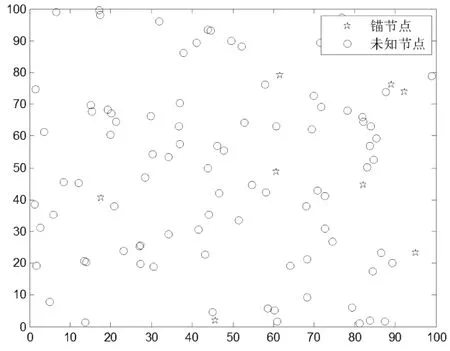
图3 仿真环境节点分布
在相同锚节点覆盖率和不同通信半径下,仿真原DV-Hop算法﹑文献[4]DV-Hop算法﹑文献[5]双通信半径的DV-Hop算法﹑文献[6]双通信半径的DV-Hop算法以及本文改进的DV-Hop算法的定位精度。由于节点分布的随机性,程序仿真100次,结果如图4所示。
定位精度是评判一个定位算法的重要指标,值越小说明定位误差越小,定位性能越好。由仿真可见,本文改进算法比文献[5]及文献[6]算法,定位精度大大提高。通信半径50 m时,由实验数据可得本文比文献[6]算法提高定位精度15%。
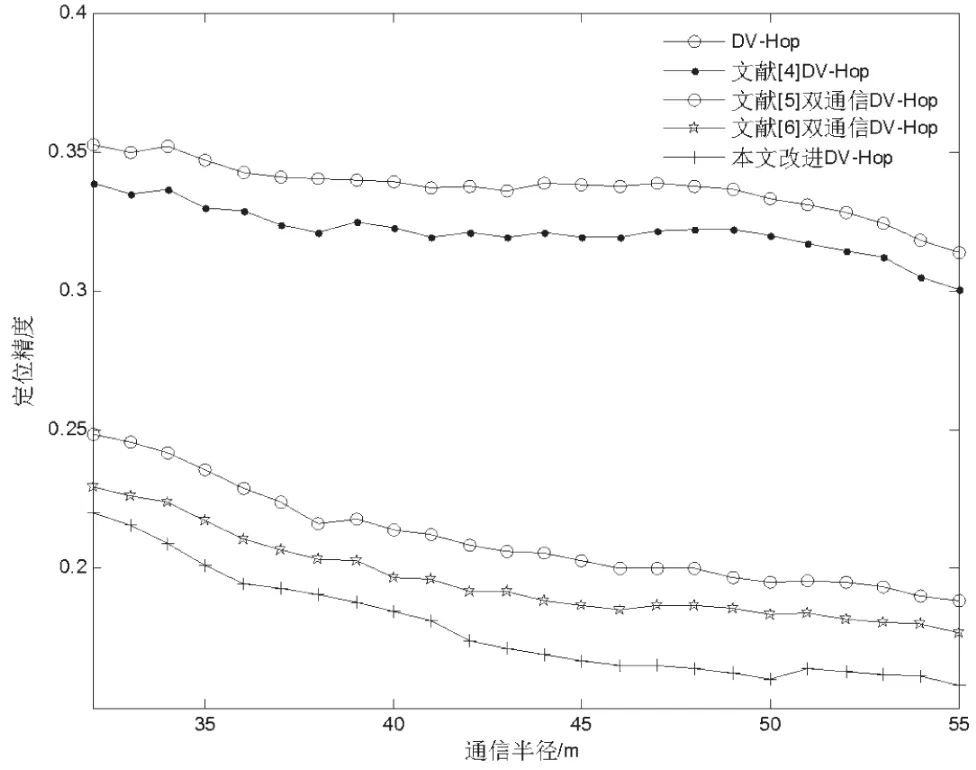
图4 五种算法对比
3.2 基于双通信半径的最佳跳数加权算法性能比较
由于在双通信半径算法中,如果未知节点到锚节点的距离在R/2到R范围内,跳数值均记1,导致节点距离在R/2到R范围内的节点均被认为其分布在以该锚节点为圆心R/2为半径的圆上。由锚节点和未知节点的分布可以观察到,在随机分布的环境中,这种分布的几率几乎为零。所以,原有双通信算法存在较大误差。因此,本文将跳数变换给定,经过多次仿真得出图5,求出双通信半径中的最佳跳数给定值。
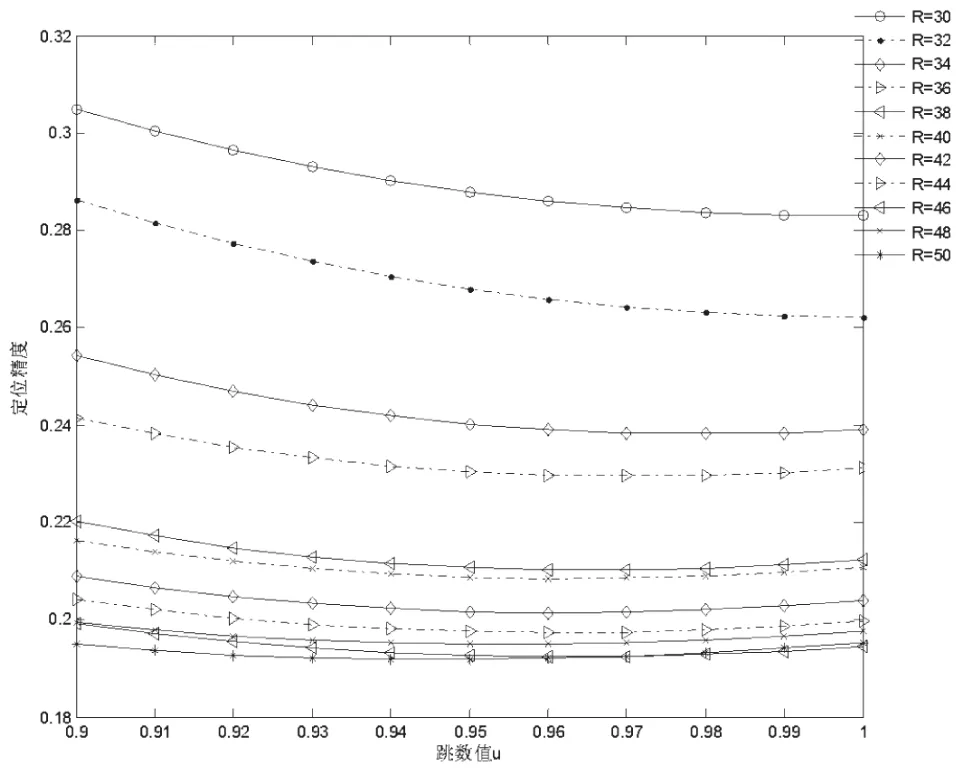
图5 求最佳跳数
经过多次仿真实验发现,锚节点覆盖率9%。例如,文献[6]跳数值取1时,误差较大,当精度精确到0.01时,可以得到更佳的u值。多次试验发现,不同的锚节点覆盖率和通信半径都会影响u的取值,但最佳跳数取值均在0.94~0.96之间。由于节点分布的随机性,程序仿真100次。如图6所示,在不同的通信半径下,本文算法比文献[6]算法定位精度高约3%。
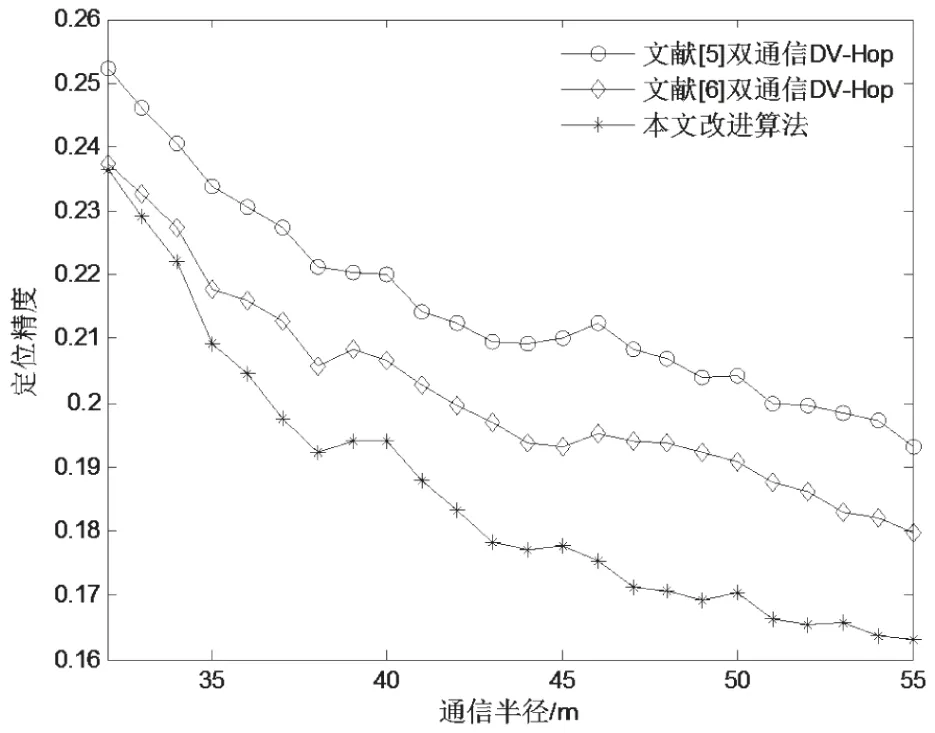
图6 三种算法对比
为了进一步验证本文改进算法的定位性能,仿真不同锚节点覆盖率和不同通信半径下的改进。由于文献[6]中已经给出文献[5]与文献[6]的精度比较,本文不再赘述,这里只给出两种精度更高的算法比较,结果如图7所示。可见,本文算法精度较文献[6]进一步提高。
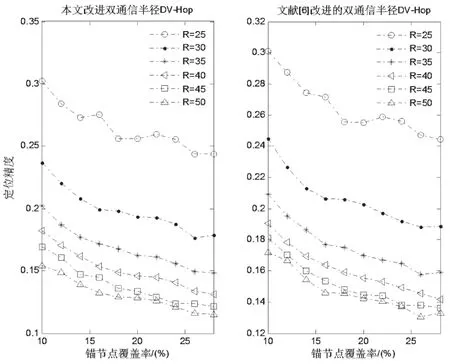
图7 两种算法对比
4 结 语
本文针对DV-Hop算法的不足,提出了一种多跳数变换的双通信算法。仿真实验表明,基于该方法改进的DV-Hop算法能减小定位误差,具有有效性。但是,由于该方法存在累积定位误差以及能耗增多方面的影响,因此需进一步研究改进。
[1] 彭力.无线传感器网络技术[M].北京:冶金工业出版社,2011:2.
PENG Li.W ireless Sensor Network Technology[M]. Beijing:Metallurgical Industry Press,2011:2.
[2] HU Juan,JIANG M in-lan.An Im p roved Node Localization Algorithm in Wireless Sensor Network[C]. Advanced Research and Technology in Industry App lications(WARTIA),2014 IEEE W orkshop on,2014:398-401.
[3] WANG Chen.An Improved DV-distance Localization Algorithm for Wireless Sensor Networks[C].Advanced Computer Control(ICACC),2010:472-476.
[4] 马淑丽,赵建平.WSN中基于最佳指数的加权DVHop算法[J].通信技术,2015,48(10):1147-1151.
MA Shu-li,ZHAO Jian-ping.W eighted DV-Hop A lgorithm based on Op timal Index in WSN[J]. Communications Technology,2015,48(10):1147-1151.
[5] 李娟,刘禹,钱志鸿.基于双通信半径的传感器网DV-Hop定位算法[J].吉林大学学报:工学版,2014,44(02):502-507.
LI Juan,LIU Yu,QIAN Zhi-hong.Improved DV-Hop Localization Algorithm based on Two Communication Ranges for W ireless Sensor Network[J].Journal of Jilin University(Engineering and Technology Edition),2014,44(02):502-507.
[6] 赵建平,马淑丽.基于双通信半径的DV-Hop改进算法[J].通信技术,2015,48(12):1406-1410.
ZHAO Jian-p ing,MA Shu-li.The Best Index Weigh ted DV-Hop A lgorithm based on Doub le Communication Radius[J].Communications Technolo gy,2015,48(12):1406-1410.
[7] 冯江,朱强,吴春春.改进的DV-Hop定位算法研究[J].计算机工程,2012,38(19):74-81.
FENG Jiang,ZHU Qiang,WU Chun-chun.Research on Improved DV-Hop Localization Algorithm[J].Computer Engineering,2012,38(19):74-81.
[8] 黄炎炎,陈向东,倪进权等.改进的DV-Hop无线传感器网络定位算法[J].通信技术,2014,47(07):765-769.
HUANG Yan-yan,CHEN Xiang-dong,NI Jin-quan,et al.An Imp roved DV-Hop Localization A lgorithm for W ireless Sensor Networks[J].Communications Technology,2014,47(07):765-769.
[9] 刘士兴,黄俊杰,刘宏银等.基于多通信半径的加权DV-Hop定位算法[J].传感技术学报,2015,28(06):883-887.
LIU Shi-xing,HUANG Jun-jie,LIU Hong-yin.An Improving DV-Hop A lgorithm based on Multi Communication Radius[J].Chinese Journal of Sensors and Actuators,2015,28(06):883-887.
[10] Savarese C,Langendoen K,Rabaey J M.Robust Positioning Algo-rithms for Distributed Ad-Hoc Wireless Sensor Networks[C].Monterey:USENIX Technical Annual Conference,2001.
[11] 魏全瑞,刘俊,韩九强.改进的无线传感器网络无偏距离估计与节点定位算法[J].西安交通大学学报,2014,48(06):1-6.
WEI Quan-rui,LIU Jun,HAN Jiu-qiang.An Improved DV-hop Node Localization Algorithm based on Unbiased Estimation for W ireless Sensor Networks [J].Journal of Xi’an Jiaotong Unibersity,2014,48(06):1-6.
[12] 嵇玮玮,刘中.DV-Hop定位算法在随机传感器网络中的应用研究[J].电子与信息学报,2008,30(04):970-974.
JI Wei-wei,LIU Zhong.Study on the Application of DV-Hop Localization Algorithms to Random Sensor Networks[J].Journal of Electronics & In formation Technology,2008,30(04):970-974.
M odified Localization Algorithm based on DV-hop
MENG Wen-wen, ZHAO Jian-ping, WANG Meng, YANG Heng-yao, ZHANG Hao
(College of Physics Engineering, Qufu Normal University, Qufu Shandong 273165, China)
Node localization technology is one of the key technologies in wireless sensor networks. DVHop localization algorithm based on the double communication radius, as compared with the traditional algorithms, could fairly improve the positioning accuracy, and however, this accuracy still has the space to be further improved. Based on the double communication radius location algorithm, the formula for calculating the average hop distance of anchor nodes is improved by using the concept of hop value transformation, and in combination with the weighted average per hop distance. MATALB simulation indicates that the proposed algorithm based on the double communication radius algorithm of DV-Hop algorithm, can improve the positioning accuracy. In addition, this modified algorithm could not increase hardware cost of the node.
WSN; node localization; double communication radius DV-Hop; weighted DV-Hop

TP212.9;TN929.5
A
1002-0802(2016)-11-1447-06
10.3969/j.issn.1002-0802.2016.11.007
孟雯雯(1990—),女,硕士研究生,主要研究方向为无线传感器网络﹑无线通信技术;
赵建平(1964—),男,教授,主要研究方向为无线通信技术;
王 蒙(1990—),男,硕士研究生,主要研究方向为无线传感器网络﹑无线通信技术;
杨恒耀(1990—),男,硕士研究生,主要研究方向为无线传感器网络﹑无线通信技术;
张 浩(1990—),男,硕士研究生,主要研究方向为无线传感器网络﹑无线通信技术。
2016-07-13;
2016-10-12 Received date:2016-07-13;Revised date:2016-10-12
国家自然科学基金资助项目(No.11404185);山东省高等学校科技计划项目资助(No.J12LN 08);曲阜师范大学技术开发项目(No.hxkj2015017)
Foundation Item:National Natural Science Foundation of China(No.11404185);Science and Technology Project of Higher Education of Shandong Province(No.J12LN08);Qufu Normal University Technology Development Project(No.hxkj2015017)

