启发式教学法在线性代数教学中的应用研究
——以Cramer法则为例
杨涌 文军 海昕
(国防科学技术大学理学院)
启发式教学法在线性代数教学中的应用研究
——以Cramer法则为例
杨涌 文军 海昕
(国防科学技术大学理学院)
与其他数学公共课程相比,线性代数课程具有内容抽象的突出特点。以Cramer法则教学内容为例,基于教学难点,结合教学实践和体会,探讨了启发式教学法在线性代数教学中的应用。
线性代数;启发式教学法;数学课程
线性代数是很多工程技术知识的基础,因此对非数学专业而言,线性代数课程是最重要的基础数学课程之一。线性代数课程的学时一般较少,但是概念和方法很多,并且表述抽象,这样就使一些看似简单的基本概念和方法对于学生而言在学习时也有难理解、难掌握的感觉,从而导致学习过程中的困惑、失落和畏难情绪。
导致这种难学难懂状态的基本原因可以从课程的特点和学生的基础两个方面进行分析:线性代数课程使用的教材一般注重逻辑的严谨性和表述的数学化,重点突出理论知识,用纯数学方法和技巧来描述普适性的规律,强调培养学生的抽象思维能力;而大一新生的数学知识与思维能力还局限于中学阶段,并未完全具备严谨的抽象理解和推理技能。因此当课程中的知识体系与学生已学知识没有太多联系,并且内容高度抽象,表面上与后续专业课程结合不紧密时,就会使学生对线性代数课程的认识形成难学并且不实用的直观印象。
从一般的认知规律而言,人们对于自然现象的分析都遵从由特殊到一般,由具体到抽象的过程。如何在线性代数课程的教学中按照认知规律,以学生为中心对教学方法进行改进和完善,培养学生的学习兴趣,使线性代数的教学能够做到易教易学是近年来线性代数教学工作者关心的重点问题之一。本文结合线性代数课程教学实践,以Cramer法则的证明为例,探讨启发式方法在实际教学中的应用。
一、对启发式教学法的认识
启发式教学法源于中国古代儒家的教育思想。在现代教育中,启发式教学被认为是一种可以有效开发学生创造性,培养学生主动思考和自主学习能力的教学模式。在具体实施中强调以学生为基本出发点,发挥好老师的主导作用,无论对学生还是老师都提出了更高的要求。
启发式教学法的实施就是教师从学生已有知识和思维模式出发,通过创设具有启发性的情境以及适时的思维指导,激活学生的思维,引导学生主动思考并达成教学目标。
线性代数课程旨在培养学生的抽象思维和形象思维能力以及学会把握这两种思维之间的联系,让学生探索对数学问题本质的理解,提高学习的主动性和解决问题的能力。因此能否将抽象的知识理论与学生认知结构中已有的知识建立起自然而内在的联系,直接决定了教学效果的优劣。
针对启发式教学法和线性代数课程教学的要求,在线性代数教学中引入启发式方法,引导学生将思维和情感融入教学过程中,从而生成积极而有效的教与学的有机过程将明显提高学生的学习积极性,从而改善教学效果。
二、启发式教学法在Cramer法则证明中的应用及实效分析
本节以Cramer法则的部分教学内容为例,浅谈启发式教学法在线性代数教学中的具体应用。
教学内容:Cramer法则是我校自编教材《线性代数与解析几何》第一章第五节的内容,具体内容如下:
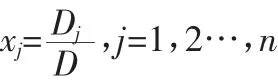
其中Dj是把D的第j列换成常数列所得到的行列式,
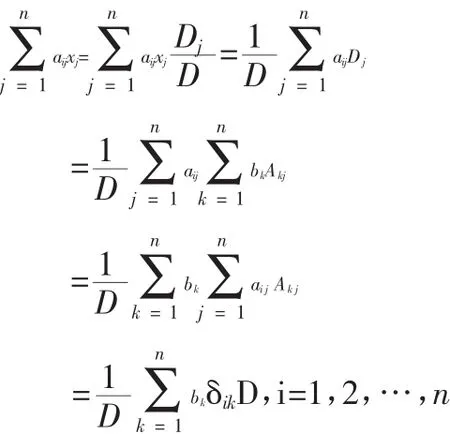
……
(唯一性的证明略)
教学难点分析:Cramer法则的结论简洁直观,结论的证明过程具有高度的概括性和抽象性,具有显著的“数学之美”,但在实际教学过程中发现,对于初学线性代数的大一新生而言要较好地理解上述证明过程具有一定的难度。
学生学情分析:学生在学习该内容之前已经在第一节中利用中学阶段学习的线性方程组求解结果得到了关于二阶行列式和三阶行列式的相关结论;在之后的章节中已经学习过n阶行列式的系统理论,已经具备了掌握上述证明过程的基本知识。但对于此时接触线性代数知识体系只有两周左右的大一新生,在抽象表述和思维能力方面还具有一定的局限性,要理解好证明过程具有一定的难度,特别是与多维坐标相联系的求和抽象表示符号上难以很好地掌握。
教学难点破解:结合教学难点和学情分析,考虑到自然规律认知过程,在具体教学实施过程中引入了启发式教学法,做如下设计: