希尔伯特空间的序列弱完备性

代 兵，艳 艳 ，包玉娥

(内蒙古民族大学 数学学院,内蒙古 通辽 028043)



希尔伯特空间的序列弱完备性

代 兵，艳 艳 ，包玉娥

(内蒙古民族大学 数学学院,内蒙古 通辽 028043)

在内积空间中引进一种弱收敛性概念,并研究希尔伯特(Hilbert)空间的序列弱完备性问题.首先,在内积空间中引进了一种序列的弱收敛性——弱内积收敛性概念,并讨论了弱内积收敛序列的有关性质,证明了序列弱内积收敛点的唯一性、弱内积收敛序列的有界性等;其次,在内积空间中引进了弱基本序列及序列弱完备性的概念,并证明了Hilbert空间是序列弱完备空间.

内积空间；Hilbert空间；弱内积收敛；弱基本序列；序列弱完备性

在线性空间(向量空间)中,为了讨论向量的角度和长度引进了一种结构—内积的概念.具有内积结构的线性空间叫作内积空间,完备的内积空间叫作希尔伯特空间或称Hilbert空间.

Hilbert空间是欧几里得空间的一种自然推广,是泛函分析的重要研究对象. Hilbert空间在分析数学的各个领域中有着深厚的理论基础,也是描述量子物理的基本工具.它已经被广泛地应用于数学和物理的各个分支,如积分方程、微分方程、函数论、调和分析、数学物理以及量子物理学等等.因此,有关Hilbert空间理论的研究不仅有着深刻的理论意义,而且有着广泛的应用价值.

在Hilbert空间的一些理论及应用中,序列的收敛性概念起着非常关键的作用[1-6].本文在内积空间中给出一种弱收敛性—弱内积收敛性概念,并研究Hilbert空间的序列弱完备性问题.

1 预备知识

本节首先介绍内积空间和Hilbert空间的基本概念及有关性质,内容均来自于文献[7-10].

定义1设X是数域K上的线性空间，若定义在X×X上的二元函数〈·,·〉,满足条件：

(ii)〈αx,y〉=α〈x,y〉,∀x,y∈X,α∈K；

(iii) 〈x+y,z〉=〈x,z〉+〈y,z〉,∀x,y,z∈X；

(iv) 〈x,y〉≥0,∀x∈X，且〈x,x〉=0当且仅当x=0，

则称〈x,y〉为x与y的内积，(X,〈·,·〉)称为内积空间.

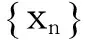
‖xn-xm‖<ε

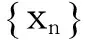
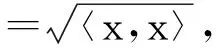
设‖·‖为由内积〈·,·〉导出的范数,则对任何x,y∈X,有Schwarz不等式：

当且仅当向量x与y线性相关时等号成立.

定理1(Riesz表示定理) 设X是Hilbert空间,f是X上的连续线性泛函,则存在唯一的y∈X,使得：

f(x)=〈x,y〉,x∈X

定义3设(X,〈·,·〉)为内积空间,E⊂X.且满足条件：

(i) 〈x,y〉=0,∀x,y∈E且x≠y；

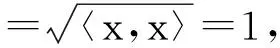
则称E为X中的标准正交集.

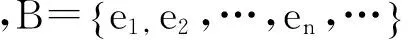
且cn=〈x,en〉,n=1,2,….

2 内积空间的弱收敛性

本节在内积空间中,引进一种序列的弱收敛性——弱内积收敛性概念,并讨论其相关的性质.

定义4设xn(n=1,2,…)为内积空间(X,〈·,·〉)中的序列,如果对任何x∈X,存在x0∈X,使得〈x,xn〉在数域K中收敛于〈x,x0〉,即：

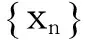
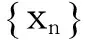
证明设:

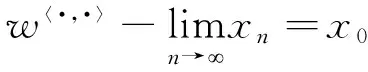
则由定义4,对任何x∈X,有:

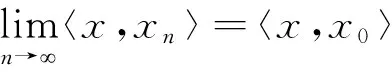
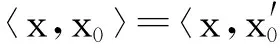
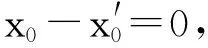
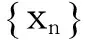
‖xn‖

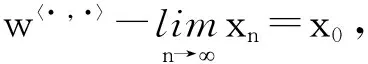
从而存在N>0,当n>N时,有:

所以当取x=xn-x0时,有:

从而易推出:

‖xn‖-‖x0‖<1

即当n>N时,有‖xn‖<‖x0‖+1.取:

则有:

证明设:

则由定义4,对任何x∈X有:

于是由数列极限的迫敛性,对任何x∈X,有:

证明(i)设:

则由定义4,对任何x∈X,有:

所以由定义1的条件(iii)和定义4,有:

从而由定义4,有：

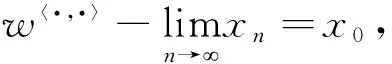
所以由定义1的条件(i)和(iii)和定义4,对λ∈K,有：

从而由定义4,有：

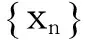
证明对任何x∈X,由定义1的条件(iii)和Schwarz不等式,有：

‖x‖‖xn-x0‖

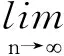
3 Hilbert空间的序列弱完备性

本节在内积空间中,引进弱基本序列及序列弱完备性概念,并讨论Hilbert空间的序列弱完备性问题.

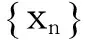
如果(X,〈·,·〉)中的弱基本序列都弱内积收敛于X中的点,则称X为序列弱完备空间.

引理1设X为Hilbert空间,E⊂X.如果对任何y∈X,都存在只与y有关的常数a(y),使得对任何x∈E,都有：

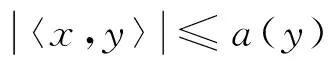
则E为有界集.

证明假设E无界,则取x1∈E,使得‖x1‖>1,令：

取x2∈E,使得：

‖x2‖>22(a(un)2)>22‖x1‖>4

令：

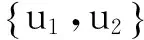
这样做下去(进行n-1次)就可以得到X中的标准正交集：

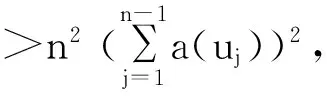
则由：

有：

从而‖xn‖>n2.

于是由u1,u2,…,un-1的标准正交性,有:

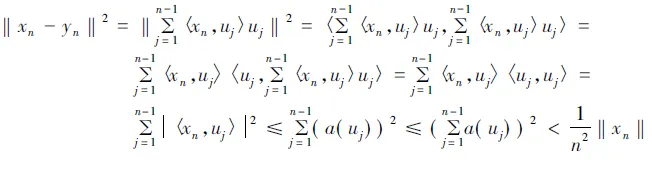
所以:

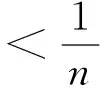
从而当n≥2时,有:

(1)

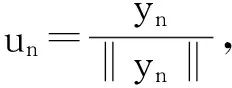
(2)

所以有:

(3)

于是由式(2)和(3)及已知条件,有:

又因为:

从而:

所以:

(4)

令n→+则由式(4),有a(z)=+.这与已知条件a(z)为常数相矛盾,即E有界.

定理5设X为Hilbert空间,则X为序列弱完备空间.

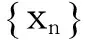
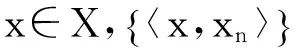
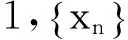
则对任何x,y∈X及α,β∈K,由定义1的条件(2)和(3),有:

即f为X上的线性泛函.

又由Schwarz不等式,有:

‖x‖‖xn‖≤β‖x‖

(5)

令n→,则由式(5),有‖x‖,x∈X.从而f成为X上的连续线性泛函.

于是由定理1,存在唯一的x0∈X,使得f(x0)=〈x,x0〉.

所以对任何x∈X,有:

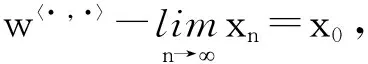
4 结论

序列的收敛性概念,在Hilbert空间的一些理论及应用中起着非常关键的作用.本文主要研究了 Hilbert 空间的序列弱完备性问题.首先在内积空间中给出了一种弱收敛—弱内积收敛性概念及其相关性质,并证明了内积空间中的收敛序列一定弱内积收敛.其次,讨论了 Hilbert 空间的序列弱完备性问题,并证明了Hilbert 空间是序列弱完备空间.这些结果对在 Hilbert空间中，建立压缩映像族的弱收敛定理和向量均衡问题的弱收敛定理等相关弱收敛性理论打下了良好的理论基础.

[1] 陈汝栋,张辉文,王洁,等.希尔伯特空间中分裂等式不动点问题的强收敛性[J].西南大学学报(自然科学版),2015,37(12):80-84.

[2] 肖建中,严洁,朱杏华.Hilbert空间中非扩张余弦族的显式、隐式和黏性迭代[J].数学物理学报,2014,34(6):1518-1531.

[3] 张基益.Hilbert空间中渐近非扩张型半群殆轨道的强遍历收敛定理[J].西南大学学报(自然科学版),2014,35(12):83-87.

[4] 傅湧.Hilbert空间中非扩张映射的Noor混合式迭代序列的收敛性[J].浙江大学学报(理学版),2011,38(1):22-26.

[5] 郭训香.Hilbert空间中g-框架类展开式与 g-Riesz-Fischer 序列[J].中国科学:数学,2016,46(4):467-480.

[6] 王波,胡长松.Hilbert空间中变分不等式与最小范数不动点问题的Noor三步算法收敛性研究[J].湖北师范学院学报(自然科学版),2014,34(4):68-73.

[7] 粟塔山.讲授 Riesz表示定理的两点注记[J].大学数学,2012,28(4):133-135.

[8] 穆蕊萍.里斯表示定理的形成过程[D].西安：西北大学,2014:17-21.

[9] 刘培德.泛函分析基础[M].北京:科技出版社,2006:32-136.

[10] 黎永锦.泛函分析讲义[M].北京:科技出版社,2011:162-170.

责任编辑：高 山

Weakly Sequential Completeness of Hilbert Spaces

DAI Bing,YAN Yan,BAO Yu′e

(College of Mathematics,Inner Mongolia University for Nationalities,Tongliao 028043，China)

In this paper,we introduce a concept of the weak convergence in the inner product space, and research the problem about the weak sequential completeness of Hilbert space.Firstly,we introduce a concept of weak convergence of a sequence in the inner product space,which is called the weak convergence in inner product space.And we discuss the property of weak convergent sequence in inner product space.The properties like the uniqueness of the weakly sequental convergent point in inner product space and the boudedness of weak convergent inner product sequence are proved. Secondly,we introduce the concepts of basic weak sequence and weakly sequential completeness,and prove that the Hilbert space is a space whose sequence is weakly complete.

inner product space; Hilbert space;weak inner product convergence;weak basic sequence;weak sequential completeness

2016-06-12.

内蒙古自然科学基金项目(2010MS0119).

代兵(1991- )，女，硕士，主要从事泛函分析与模糊分析的研究；*

包玉娥(1962- )，女(蒙古族)，博士，教授，主要从事泛函分析与模糊分析的研究.

1008-8423(2016)04-0380-06

10.13501/j.cnki.42-1569/n.2016.12.005

O177.91

A