多项学习免疫优化算法

张伟伟，林静静，景红蕾，林雪洁

(1.郑州轻工业学院 计算机与通信工程学院，河南 郑州 450000；



多项学习免疫优化算法

张伟伟1，林静静1，景红蕾1，林雪洁2

(1.郑州轻工业学院 计算机与通信工程学院，河南 郑州 450000；

2.郑州大学 电气工程学院，河南 郑州 450000)

提出了多项学习免疫优化算法OL-CAIS求解全局优化问题.将混沌优化理论加入到免疫算法中，同时在算法中引入一个类杂交算子的搜索方程，更注重整个群体的交互信息，重新定义了搜索方式，然后，通过正交实验构造一个正交学习策略充分利用了搜索空间中的有用信息、正交设计小样本特性，产生更优秀的子代，保证多样化的有效搜索.

人工免疫；混沌优化；杂交算子；正交学习

1986年Farmer发表的论文“The immune system,adaptation and machine learning”[1]中提出了一个基于Jerne的网络假说动态免疫系统模型，并探讨了免疫系统与其他智能方式的关联.由人体免疫系统的进化理论，De Castor提出了人工免疫网络模型(aiNet)，并为解决多模态函数优化问题作了进一步的改进，传统aiNet优化算法[2]由此诞生.李春华等[3]对亲和力阈值、相似度阈值等几个参数做了研究，提出了基于参数优化的自适应人工免疫算法.受微粒群优化算法[4]启发，引入精英学习机制，提出用于优化问题的高效人工免疫网络算法(EaiNet)[5]，每个独立的个体总是向种群中最优秀的个体学习，从而提高了算法的收敛速度.但大量的研究也表明免疫算法也存在早熟收敛、搜索能力差、计算量大等诸多不足和缺憾.

基于前述的研究成果和存在的问题，本文将对免疫系统主要的进化算子进行改进，提出一种全新的具有基于多项学习的免疫优化算法(OL-CAIS)，目的在于加快收敛速率、提高求解质量.

1 相关基础理论

1.1 全局优化

全局优化问题是工程领域普遍存在的一类数学规划问题，具有重要的研究意义.一般的全局优化问题可以描述为:

其中：N表示决策变量个数，f(x)为目标函数，[lb,ub]为可行解空间.人工免疫算法是受生物免疫系统启发而设计的一种新型智能优化算法，采用群体搜索策略，在搜索过程中能够更好的收敛到全局最优解.

1.2 免疫系统

克隆选择算法[6]是生物免疫算法中的基本算法之一.在克隆选择算法中，需要解决的问题被映射为抗原，问题的解被映射为抗体.免疫克隆选择算法的主要流程如算法1所示.

算法1 免疫克隆选择算法Algorithm 1 Immune clonal selection computation

2 多项学习免疫优化算法

2.1 混沌初始化种群

混沌(Chaos)变量看似杂论无章却内含规律.混沌理论可以用于免疫算法在解空间产生出均匀分布的初始种群，以提高免疫算法的计算精度和收敛速度[7].常用混沌动力学映射分岔图如下：

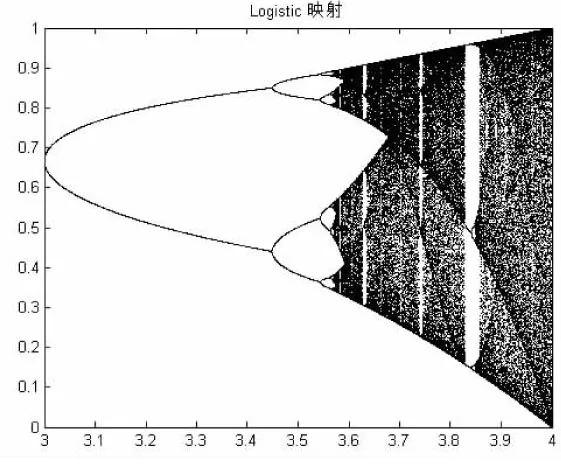
图1 Logistic映射分岔图Fig.1 Mapping bifurcation diagram of Logistic

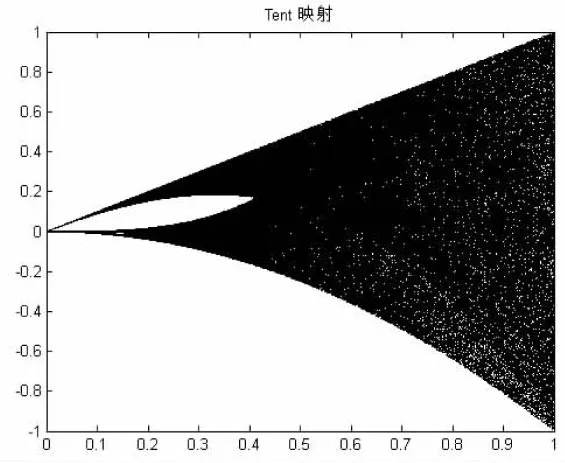
图2 Tent映射分岔图Fig.2 Mapping bifurcation diagram of Tent

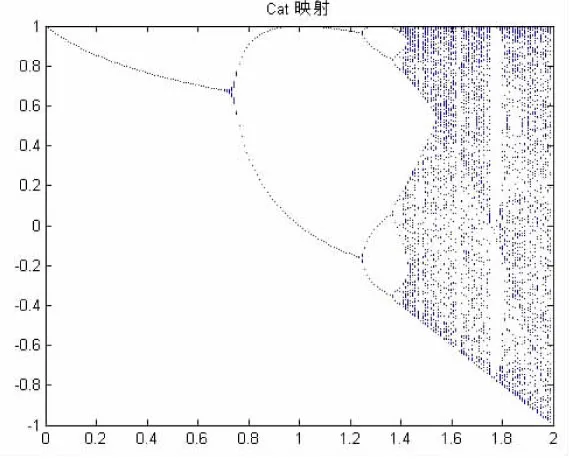
图3 Cat映射分岔图Fig.3 Mapping bifurcation diagram of Cat

图4 三种映射取值分布曲线Fig.4 Mapping values distribution curve of Three kinds

图5 Cat映射产生初始种群在解空间的分布Fig.5 Initial population distribution of Cat in the solution space

比较而言，Cat映射具有更好的均匀性且混沌优化过程中不易陷入小循环，故采用经典Cat映射模型来产生用于混沌免疫算法的初始种群.Cat映射模型计算公式如式1所示：

(1)

式中：n表示混沌变量的序号；i表示种群序号；(xn,yn)表示一个二维混沌变量. 设定种群规模为100，用式(1)混沌产生初始种群.图5为初始种群在解空间的分布.

2.2 杂交算子的搜索方程

一些经典免疫算法如opt-aiNet、IA-AIS使用的是单个种群，所有的抗体独立进化，这将降低收敛速度，引入学习机制，CAIS将免疫分为获得性免疫和固有免疫，一个进化后的子代不仅承载来自父代的变异信息，更注重整个群体的交互信息，同时为解决人工免疫算法在实际应用中存在的缺点，如算法后期收敛速度较慢，搜索过程也可能出现早熟，最重要缺少交叉操作，这时候增加类似交叉操作的杂交算子更能维持种群的多样性.即:

Abi(t+1)=Abi(t)+G1·λi(t),innate and Abi(t+1)=Abr1(t)+φi,j(Abr1(t)-Abr2(t)),adaptive

(2)

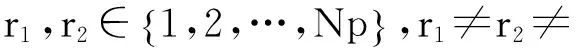
2.3 OL策略

由于AIS算法较弱的学习机制，不能很好地执行系统的搜索，故本文采用正交设计的方法形成一个正交学习(OL)策略来产生一个更优秀的候选解.为了增加搜索的多样性，当执行OL策略时，传递向量Ti通过下式产生：

Ti=Xk+rand(0,1)(Xbest-Xk),

(3)

每一维对实验的影响定义如下：

(4)

其中，fm表示第m次实验的结果；当第m次实验中因素n的水平为q时，zmnq=1，否则，zmnq=0.

算法2 正交学习策略Algorithm 2 Orthogonal learning strategies

2.4 算法框架

本文提出了基于多项学习的免疫优化算法OL-CAIS.利用免疫算法各环节具有很强的独立性和扩展性，提出将混沌优化理论加入到免疫算法中，在算法中引入精英类杂交算子的搜索方程，重新定义了搜索方式，为了充分利用搜索空间中的有用信息，通过正交设计构造一个正交学习策略.正交学习策略利用正交设计小样本特性，产生更优秀的子代，保证多样化的有效搜索.OL-CAIS算法的整体框架如算法3所示.

算法3 多项学习的免疫优化算法OL-CAISAlgorithm 3 Multiple learning immune optimization algorithm

3 仿真实验

为了测试所提出算法的性能，本节通过解决6个常用的全局优化问题[8]进行实验评估OL-CAIS的性能.与传统的进化算法模型比较,并分析OL-CAIS的性能.

3.1 平台选定和参数设定

表1给出了实验中使用的测试函数.它们可以分为四种类型:f1是单峰函数，f2～f6是多峰函数.

表1 测试函数Tab.1 Test function

比较OL-AIS与Opt-aiNet，CSA算法在上述6个测试问题的10维和30维，此外与其他7个最先进的进化算法比较.列出了7个代表进化算法：差分进化算法 (SaDE)[9]；基于正交交叉微分进化(OXDE)[10]；量化正交遗传算法(OGA/Q)[11]；全面学习粒子群优化(CLPSO)[12]；进化策略与协方差矩阵适应(CMA-ES)[13]；全局和局部的实数编码遗传算法(GL-25)[14]；混合学习克隆选择算法(HLCSA)[15].种群大小设置为30，最大运行次数(mFES)设置为10 000×D.所有的实验都是独立运行30次.

3.2 实验结果和讨论

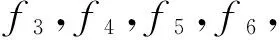
表2 改进前后算法的性能比较D=10,30Tab.2 Performance comparison of improvement algorithm D=10 and D=30

表3介绍OL-CAIS与其他7个最先进的进化算法在平均值和标准差的比较，维数为10，最好的结果以粗体显示.表4显示了OL-CAIS与其他7个最先进的进化算法在平均值和标准差的比较，维数为30，最好的结果以粗体显示.可以观察到，这些测试实例，显示OL-CAIS的可伸缩性很好处理高维优化问题.

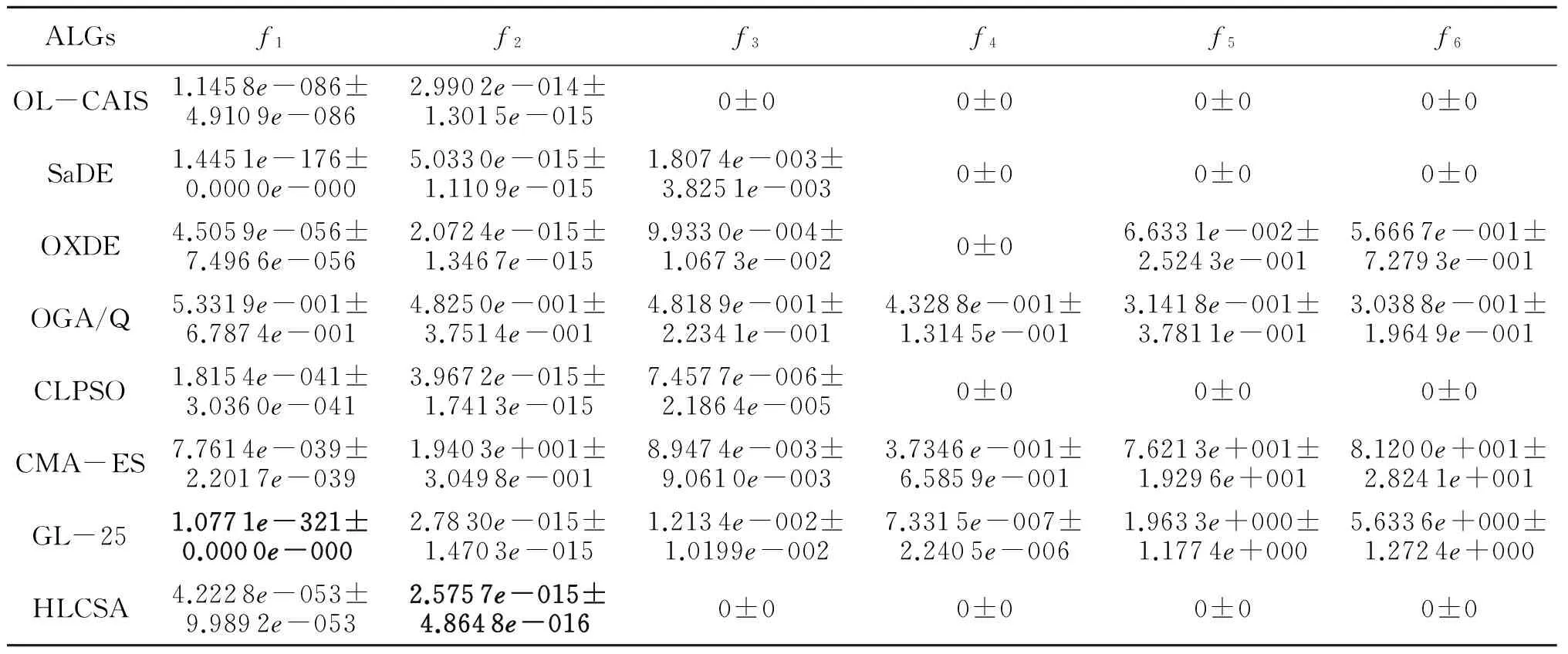
表3 7种算法的性能比较 D=10Tab.3 Performance comparison of seven kinds of algorithm D=10

4 结果与讨论

虽然传统免疫优化算法的优点在于搜索出全局最优解，但是它不能满足人们对搜索效率和求解质量的要求.相比之下，本文提出的OL-CAIS优化算法，不仅引入了学习思想和类杂交算子的搜索方程, 更注重整个群体的交互信息,通过正交设计构造一个正交学习策略，利用其正交设计小样本特性,可以产生更优秀的子代,保证多样化的有效搜索致力于平衡算法的搜索能力和开发能力.因此，OL-CAIS优化算法在最优解质量和收敛速度上比传统优化算法表现出更好的性能.

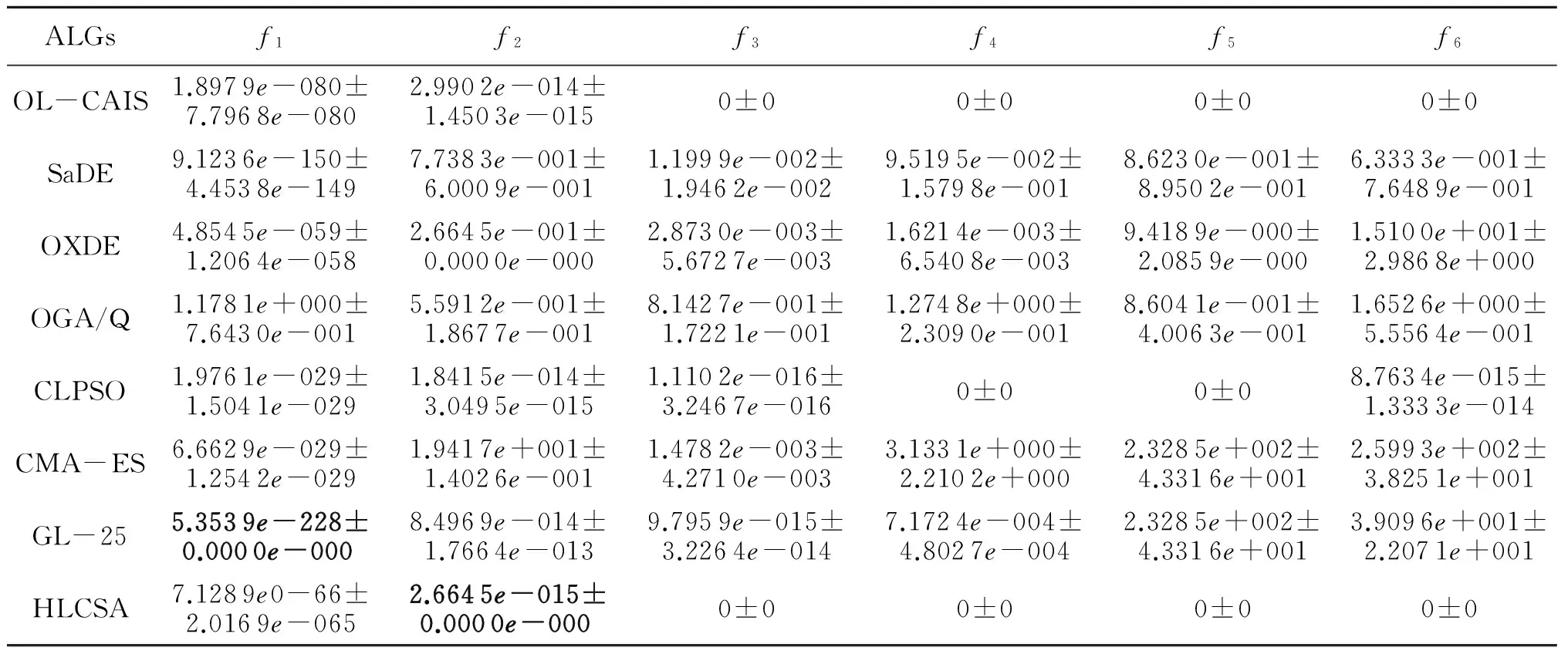
表4 7种算法的性能比较 D=30Tab.4 Performance comparison of seven kinds of algorithm D=30

[1]JDFARMER,NHPACKARD,ASPERELSON.Theimmunesystem,adaptation,andmachinelearning[J].PhysicaD:NonlinearPhenomena,1986,22(1):187-204.

[2]DECASTROLN,TIMMISJ.Anartificialimmunenetworkformultionfunctionoptimization[C]//ProceedingsofIEEECongressonEvolutionaryComputation.NewYork:IEEEPress,2002(1):699-674.

[3] 李春华,朱燕飞,毛宗源.一种新型的自适应人工免疫算法[J].计算机工程与应用,2004,40(22):84-87.

[4]BERGHF,ENGELBRECHTAP.Acooperativeapproachtoparticleswarmoptimization[C]//IEEETransactionsonEvolutionaryComputation.NewYork:IEEEPress,2004,8(3):225-239.

[5]LIZH,SHANGYN,TANHZ.Anefficientartificialimmunenetworkwithelite-learning[C]//Procdingsofthe3rdInternationalConferenceonNaturalComputation(ICNC9007).Haikou:IEEEPress,2007(4):213-217.

[6]LNDECASTRO,FJVONZUBEN.Theclonalselectionalgorithmwithengineeringapplications[C]//InProceedingsofGeneticandEvolutionaryComputationConference,2000:36-39.

[7]HEHONG,QIANFENG,DUWENLI.Achaoticimmunealgorithmwithfuzzyadaptivepara-meters[J].Asia-PacificJournalofChemicalEngineering,2008,3(6):695-705.

[8]JLIANG,PSUGANTHAN,KDEB.Novelcompositiontestfunctionsfornumericalglobaloptimization[C]//ProceedingsofIEEESwarmIntelligenceSymposium,2005:68-75.

[9]AKQIN,VLHUANG,PNSUGANTHAN.Differentialevolutionalgorithmwithstrategyadaptationforglobalnumericaloptimization[J].IEEETransEvolution,Comput,2009,13(2):398-417.

[10]YWANG,ZCAI,QZHANG.Enhancingthesearchabilityofdifferentialevolutionthroughorthogonalcrossover[J].InformSci,2012,185(1):153-177.

[11]YWLEUNG,YWANG.Anorthogonalgeneticalgorithmwithquantizationforglobalnumericaloptimization[J].IEEETransEvolutionComput,2001,5(1):41-53.

[12]JJLIANG,AKQIN,PNSUGANTHAN,etal.Comprehensivelearningparticleswa-rmoptimizerforglobaloptimizationofmultimodalfunctions[J].IEEETransEvolutionComput,2006,10(3):281-295.

[13]NHANSEN,AOSTERMEIER.Completelyderandomizedself-adaptationinevolutionstrategies[J].EvolutionComput,2001,9(2):159-195.

[14]CGARCíAMARTíNEZ,MLOZANO,FHERRERA,etal.Globalandlocalreal-codedgeneticalgorithmsbasedonparentcentriccrossoveroperators[J].EuroJOperatRes,2008,185(3):1088-1113.

[15]YONGPENG,BAOLIANGLU.Hybridlearningclonalselectionalgorithm[J].EvolutionInformationSciences,2015,296:128-146.

责任编辑：高 山

Multiple Learning Immune Optimization Algorithm

ZHANG Weiwei1,LIN Jingjing1,JING Honglei1,LIN Xuejie2

(1.College of Computer and Communication Engineering,Zhengzhou University of Light Industry,Zhengzhou 450000,China；2.College of Electrical Engineering,Zhengzhou University,Zhengzhou 450000,China)

This paper presents the immune optimization algorithm based on multiple learning OL-CAIS to solve global optimization problems.Chaos optimization theory is proposed to join the immune algorithm,and at the same time we introduced in the algorithm a class of hybrid operator search equation paying more attention to the interactive information of whole group.The search way is redefined and then,through the orthogonal experiment,an orthogonal learning strategy is formed which makes full use of the useful information in the search space and orthogonal design of small sample characteristics,to produce a better generation and ensure the effective of diverse search.

artificial immune;chaos optimization;hybrid operator;orthogonal learning

2016-10-10.

国家自然科学基金青年科学基金项目(61403349);河南省教育厅科学技术研究重点项目基础研究计划项目(14B520066；15A520033);郑州轻工业学院博士基金项目(2013BSJJ044);郑州轻工业学院研究生科技创新基金资助项目; 郑州轻工业学院大学生科技活动项目.

张伟伟(1986- ),女,博士，主要从事智能计算、优化理论的研究.

1008-8423(2016)04-0424-06

10.13501/j.cnki.42-1569/n.2016.12.015

TP391

A