基于半不变量和Gram-Charlier级数展开法的随机潮流算法

卫 鹏， 刘建坤， 周 前， 徐青山， 黄 煜

(1. 江苏省电力试验研究院有限公司，江苏 南京 211103；2. 东南大学电气工程学院，江苏 南京 210096)

·电网技术·

基于半不变量和Gram-Charlier级数展开法的随机潮流算法

卫 鹏1， 刘建坤1， 周 前1， 徐青山2， 黄 煜2

(1. 江苏省电力试验研究院有限公司，江苏 南京 211103；2. 东南大学电气工程学院，江苏 南京 210096)

随着新能源规模的日益扩大，新能源电站的出力往往呈现较强的相关性，在传统的随机潮流算法中对强相关性随机变量考虑较少。综合考虑风电出力的随机波动、负荷的变化、发电机的强迫停运及线路的故障等各种不确定情况，根据节点电压和支路潮流的期望值及灵敏度矩阵，计算了负荷及常规发电机、风电机组出力、各节点注入功率的各阶半不变量，由Gram-Charlier级数展开求得概率密度函数和概率分布函数。IEEE-30节点测试表明：该算法能反映大规模新能源接入下系统的不确定性，将求取随机变量和的概率密度函数的卷积运算简化为半不变量的代数运算，极大地缩短了计算时间，并具有良好的收敛性。

随机模型; 半不变量; 随机潮流; 风电; Gram-Charlier级数

分布式新能源发电是解决当前能源危机和环境污染问题的有效手段，随着单位电能生产成本的不断降低和政策的大力支持，大规模风电、光伏等新能源将是未来电网的重要电力来源[1]。由于可再生能源如风能、太阳能等以及负荷功率具有很大的不确定性，微网的运行控制将面临新的挑战[2]。

潮流计算是电力系统运行分析和规划设计的基础，传统潮流方法如适合辐射型网络的前推回代法和环状结构的N-R法都无法全面反映系统不确定因素的影响，并且大量新能源的接入改变了原来电网的属性，使得单一的潮流算法具有很大的局限，因此研究适应未来新能源大规模接入电网特点的潮流计算方法具有重要意义[3-8]。

本文提出了基于半不变量和Gram-Charlier级数展开的随机潮流算法，采用蒙特卡罗仿真法进行抽样，计算节点电压和支路潮流的期望和灵敏度矩阵，计算负荷、常规机组和风电机组出力的各阶半不变量，进一步得到各节点注入功率的半不变量并转换为节点状态向量和支路潮流向量的各阶半不变量，再利用Gram-Charlier级数展开，经过一次计算就可以得到节点电压和支路潮流的概率密度函数和概率分布函数。通过IEEE-30节点算例测试表明，该算法可以显著体现负荷和发电机出力的随机波动，有效求解具有强相关性的随机潮流，且具有良好的收敛性。

1 半不变量法

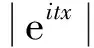
(1)

对(1)的特征函数取自然对数并在t(t=0)取较小值的邻域内展开为麦克劳林级数，则有：

(2)

式中:γν称为随机变量的ν阶半不变量;o(tk)为展开式余项。

1.1 负荷的半不变量求解方法

负荷的随机成分是由负荷预测误差和负荷的随机波动构成的，一般可用服从正态分布的随机变量描述。当负荷按某一负荷曲线变化时，可用离散分布来拟合。

对于正态分布的负荷功率，其一阶半不变量为数学期望，二阶半不变量等于方差，三阶及以上高阶半不变量的值为零[10]，即：

(3)

对于离散分布的负荷功率，先按下式求出其各阶矩：

(4)

式中：αLν为负荷变量的ν阶原点矩；pi为负荷取值xi的概率，pi=ti/T，其中ti为负荷等于xi的持续时间，T为研究周期。

1.2 常规机组出力的半不变量求解方法

常规发电机组输出功率的随机分布按两状态或多状态离散分布处理，文中的发电机组均为两状态机组，即只有正常运行和强迫停运两种状态[11]。在这种情况下，假设机组工作在额定容量C的概率为p，则输出功率为零的概率为1-p。设在某节点装有N台常规发电机组，其中有i台机组正常运行的概率为pi，可知：

(5)

则N台机组总的输出功率的各阶矩为：

αν=p1Cν+p2(2C)ν+…+pN(NC)ν

(6)

利用式(10)和(11)可求得常规发电机组输出功率的各阶半不变量。

1.3 风电机组出力的半不变量求解方法

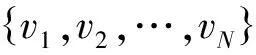
(7)

式中：αPν和αQν分别是风电机组输出有功和无功功率的ν阶原点矩。再根据原点矩和半不变量的关系可以求得风电机组出力的半不变量。

1.4 半不变量法的应用

采用半不变量计算的前提条件是随机变量之间相互独立，因此假定系统各节点注入功率的随机变量具有独立性[13]，它主要由节点负荷功率和发电机出力两部分组成，即：

ΔW=ΔWg⊕ΔWl

(8)

式中：ΔWg和ΔWl分别是节点发电机出力和节点负荷的随机变量；符号⊕表示卷积运算。根据ΔWg和ΔWl的分布情况做卷积就可以得到节点注入功率的随机变量ΔW的分布。在已知ΔW的分布后根据式(9)、(10)的线性关系，再通过卷积计算就能求得各节点状态变量ΔX和支路潮流ΔZ的概率分布[14]。

(9)

ΔZ=G0S0ΔW=T0ΔW

(10)

(11)

(12)

2 Gram-Charlier级数展开法

在得到随机变量的各阶半不变量时，可利用Gram-Charlier级数展开式逼近得到其概率密度函数和累积分布函数。在电力系统随机生产模拟中，Gram-Charlier级数可以把随机变量的分布函数展开成由正态随机变量的各阶导数所组成的级数，而级数的系数则可表示为该随机变量各阶半不变量的表达式[15]。为了简化级数的形式，定义：

(13)

式中:gν称为ν阶规格化半不变量;σ为标准差。任意一个随机变量X，假设其期望值和标准差分别为μ和σ，则其标准化的形式为：

(14)

(15)

(16)

综上所述，基于半不变量和Gram-Charlier级数展开的随机潮流算法流程如图1所示。

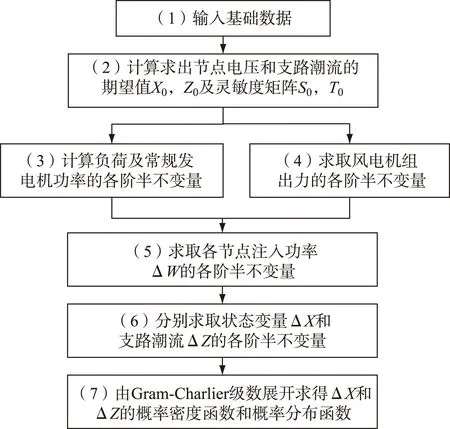
图1 随机潮流计算流程

3 算例分析

以IEEE-30节点系统为例进行仿真计算，系统有6台发电机，30个节点，41条支路，为计算方便，假设各随机变量之间相互独立，发电机的出力服从0-1分布，负荷均服从正态分布，以IEEE-30节点系统负荷值为均值，标准差为均值的20%。

算例中采用的风电场容量为3×10 MW，风电场中风机分为2排，排间距为120 m，机组以恒功率因数控制方式运行，功率因数为0.75。假设风电场内空气密度为1.224 5 kg/m3，风机的扫掠面积为1840 m2，风速的Weibull分布的2个参数k=2.17，c=8.09。单台异步风力发电机的具体参数见表1。

风电场通过变压器和110 kV线路接入IEEE-30节电系统，图2给出了修改后IEEE-30节点系统的拓扑结构。

表1 风力发电机参数

图2 IEEE-30节点系统案例模型

任选节点10、节点24、支路19-20和支路27-30为研究对象，以蒙特卡罗法(N=1000)的结果作为参照，采用文中算法进行随机潮流计算。

根据第1节内容，首先得到风电场接入前所取节点的电压幅值和支路有功功率的各阶半不变量，如表2、表3所示。

表2 节点电压幅值的各阶半不变量

表3 支路有功功率的各阶半不变量

在节点25接入风电场后，通过文中提出的蒙特卡罗抽样技术，计算出风电场出力的前七阶半不变量，如表4所示。

将求得的风电场出力的各阶半不变量与各节点原始负荷的各阶半不变量相加，即得到各节点注入功率的各阶半不变量，再通过式(14)、(15)，可以求出风电场接入后各状态变量的各阶半不变量值，如表5和表6所示。

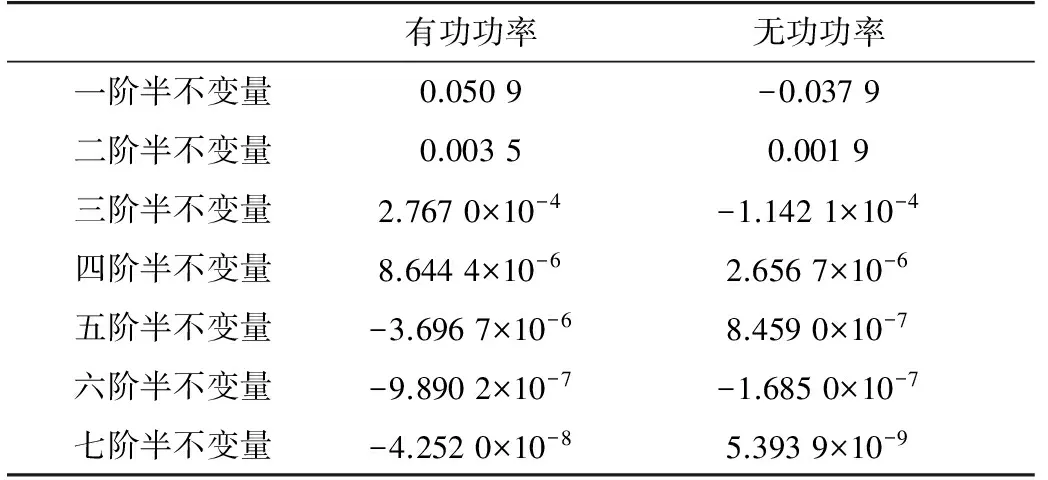
表4 风电场输出功率(有功和无功)的各阶半不变量

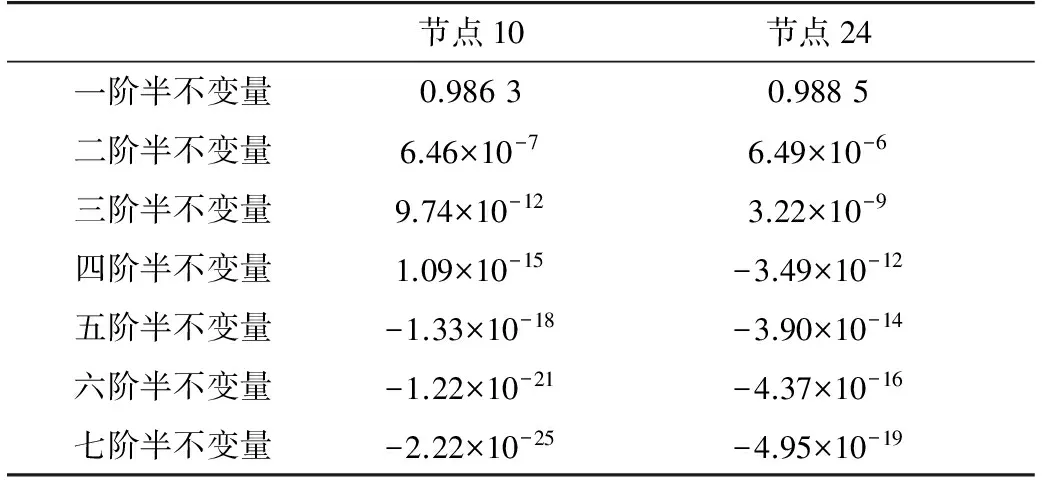
表5 风电场接入后节点电压幅值的各阶半不变量

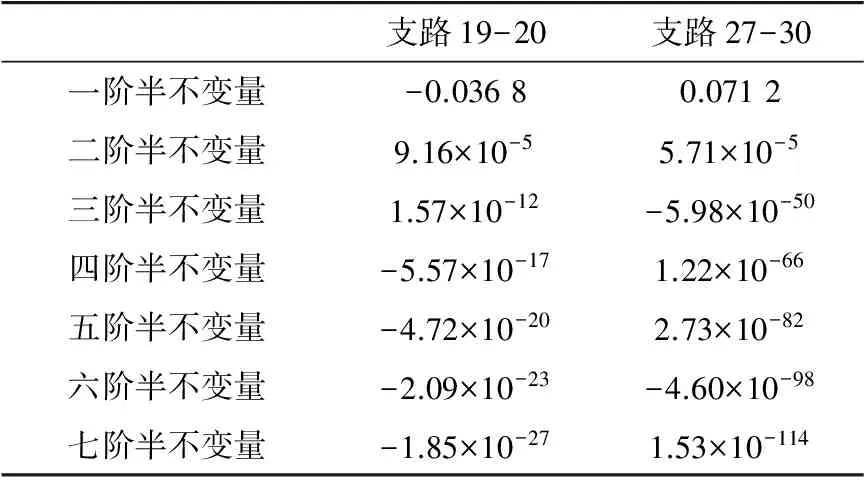
表6 风电场接入后支路有功功率的各阶半不变量

最后，取前七阶半不变量值并结合Gram-Charlier级数展开的方法，得到相应节点电压和支路潮流的概率密度函数和累积分布函数(CDF)，如图3—6所示，其中文中算法为PLF-CM算法，对比算法为蒙特卡罗法(MCS)。

为了体现本文算法所得结果的精确性，将其误差进行定量分析，采用方差和的根均值来衡量文算法和标准算法(MCS)之间的误差，表7给出了相应节点电压幅值和支路有功功率的ARMS值。

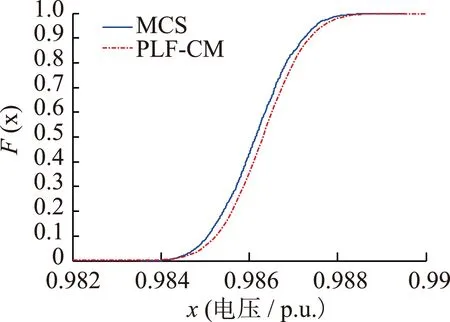
图3 节点10的电压幅值的CDF曲线

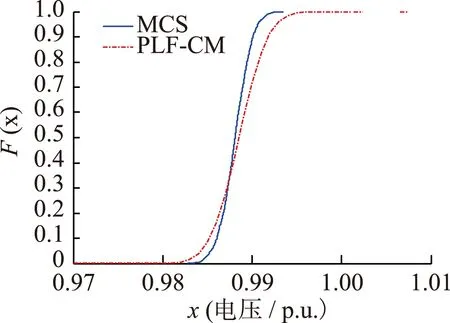
图4 节点24的电压幅值的CDF曲线

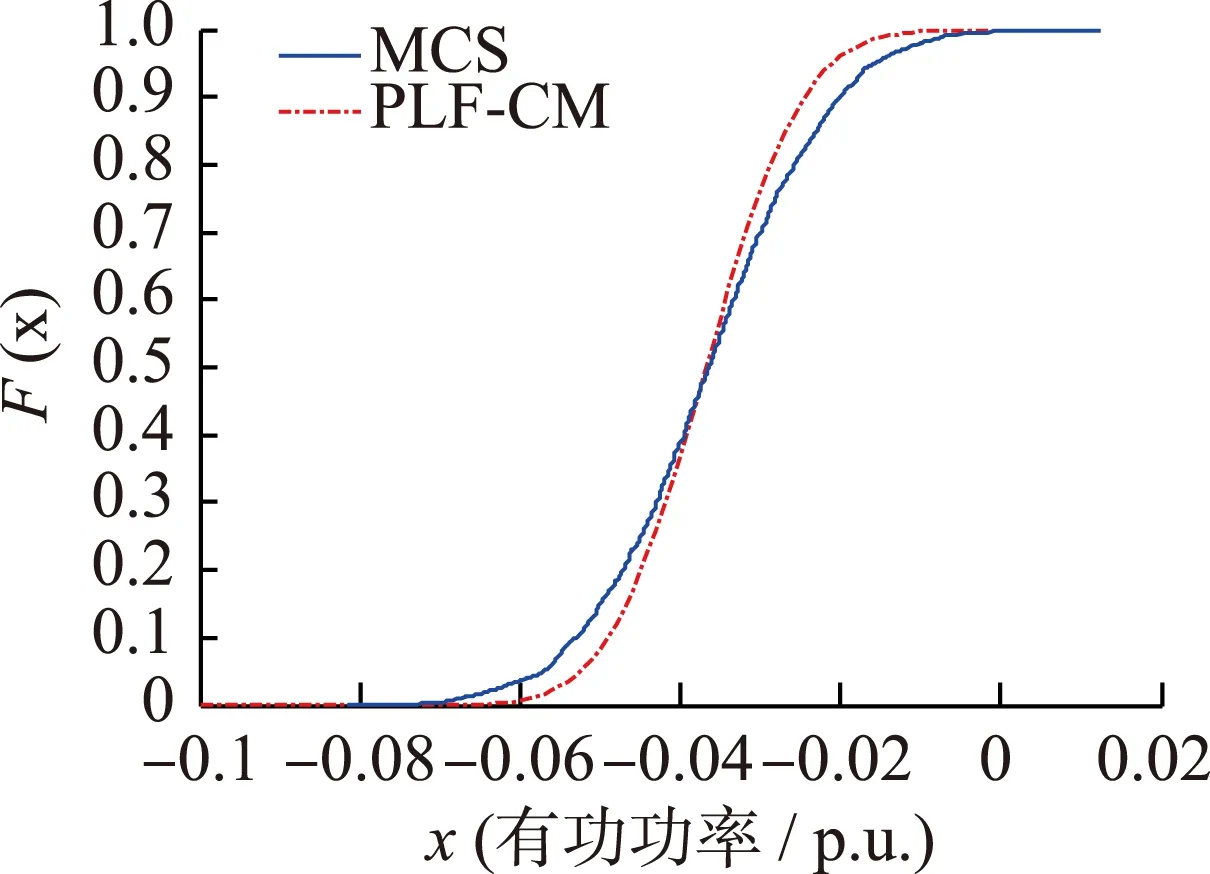
图5 支路19-20的有功功率的CDF曲线

图6 支路27-30的有功功率的CDF曲线

节点和支路ARMS/%节点100．053节点240．226支路19-200．497支路27-300．367

可以看出，所选节点和支路的相应状态量的ARMS值很小，均小于1%，说明文中算法与MCS的计算结果基本一致，具有较高的精度。文中算法和MCS算法的计算时间，分别为4.16 s，1 695.42 s，其中MCS的样本数量取10 000。可见，与MCS方法相比，文中算法在计算时间上具有显著优势，且耗时与样本数量无关。

4 结束语

风电场出力具有随机性，其大规模并网会给电力系统的稳态运行带来巨大的影响。以随机潮流为工具，建立系统的随机模型，并且提出了一种基于半不变量和Gram-Charlier级数展开的随机潮流算法，以IEEE-30节点系统为例，从计算精度和计算时间两方面比较分析了文中算法和MCS算法所得结果：(1)文算法与MCS的计算结果基本一致，具有较高的精度，且距离风电接入点越远，受随机误差影响越小；(2)文算法在计算时间上具有显著优势，且耗时与样本数量无关，在系统规模较大、需要在线潮流计算的情况下，有着广阔的应用前景。

[1] 孙国强， 李逸驰， 向育鹏， 等. 计及风速时空相关性的含风电场电力系统动态随机最优潮流计算[J]. 中国电机工程学报， 2015， 35(17)4308-4317.

[2] 陆 燕， 谈 健. 江苏海上风电接入系统若干问题探讨[J]. 江苏电机工程， 2014， 33(5): 55-58.

[3] 朱星阳， 刘文霞， 张建华. 考虑大规模风电并网的电力系统随机潮流[J]. 中国电机工程学报， 2013， 33(7): 77-85.

[4] 郭效军， 蔡德福. 不同级数展开的半不变量法概率潮流计算比较分析[J]. 电力自动化设备， 2013， 33(12): 85-90.

[5] 刘小团， 赵晋泉， 罗卫华， 等. 基于TPNT和半不变量法的考虑输入量相关性概率潮流算法[J]. 电力系统保护与控制， 2013， 22:13-18.

[6] 李新， 雷鸣，于大洋，等. 基于不变量法的含风电场电力系统随机潮流分析[J]. 电气应用，2017，31(17)：46-50.

[7] 周宜广，刘天琪. 基于混合Copula和均匀设计采样的电力系统随机潮流[J]. 中国电力，2016， 49(2)：109-113.

[8] 蒋平，杨绍进，霍雨翀. 考虑风电场出力随机性的电网静态安全分析[J]. 电力系统自动化， 2013，37(22)：35-40.

[9] 董 雷， 杨以涵， 张传成， 等. 综合考虑网络结构不确定性的概率潮流计算方法[J]. 电工技术学报， 2012， 27(1): 210-216.

[10] 石东源， 蔡德福，陈金富， 等. 计及输入变量相关性的半不变量法概率潮流计算[J]. 中国电机工程学报， 2012， 32(28): 104-113.

[11] 张李明， 齐先军. 考虑分布式电源随机性的配电网最大供电能力[J]. 电力建设， 2015， 36(11): 38-44.

[12] 戎晓雪， 别朝红， 石文辉， 等. 考虑风电场相关性的含风电电力系统随机潮流分析[J]. 电网技术， 2014， 38(8): 2161-2167.

[13] 王 彬， 何光宇， 卢建刚， 等. 考虑电网运行状态不确定性的最优潮流研究[J]. 电力建设， 2014， 35(10): 1-6.

[14] 张文婷， 范立新. 基于直流概率潮流的风电穿透功率极限计算[J]. 江苏电机工程， 2014， 33(4): 1-4.

[15] 易驰韡， 胡泽春， 宋永华等. 考虑注入功率分布的随机最优潮流方法[J]. 电网技术， 2013， 37(2): 367-371.

[16] 范钧慧， 徐 楠， 刘皓明. 含分布式风光电源的配电系统故障恢复策略[J]. 江苏电机工程， 2014， 33(1): 1-4， 8.

卫 鹏

卫 鹏(1988 —)，男，陕西宝鸡人，工程师，从事电力系统运行仿真及规划研究工作；

刘建坤(1980 —)，男，山东潍坊人，高级工程师，从事为电力系统分析及规划研究工作；

周 前(1978 —)，男，江苏无锡人，高级工程师，从事电力系统仿真及规划研究工作；

徐青山(1979 —)，男，江苏姜堰人，博士生导师，研究方向为新能源与分布式发电领域；

黄 煜(1992 —)，男，江苏扬州人，博士研究生，研究方向为新能源与分布式发电领域。

A Probabilistic Power Flow Algorithm Based on Semi-variable and Gram-Charlier Series Expansion

WEI Peng1, LIU Jiankun1, ZHOU Qian1, XU Qingshan2, HUANG Yu2

(1. Jiangsu Electric Power Research Institute Co. Ltd., Nanjing 211103, China;2. School of Electrical Engineering, Southeast University, Nanjing 210096, China)

With the growing scale of new energy, new energy power contribute often exhibit a strong correlation, traditional random flow algorithm for strong correlation random variables was considered less. A method of probabilistic power flow algorithm based on semi-variable and Gram-Charlier series expansion was proposed in this paper. According node voltage and branch current expectations and sensitivity matrix, with wind power output, load changes, forced outages and generator fault lines and other uncertainties considered, load and conventional generators, wind turbine output and each node injection power of each order half invariant were calculated. Probability density function and probability distribution function were obtained by Gram-Charlier series expansion. IEEE-30 node test shows that the algorithm can reflect the uncertainty of large-scale new energy accessing to the system, and probability density function can be simplified to the semi-invariant algebra. Greatly reduce the computation time and it has a good convergence.

stochastic model; semi-invariant; probabilistic power flow; wind power; Gram-Charlier series

2016-09-02；

2016-10-10

国家自然科学基金51577028；国家电网公司科技项目(新能源发电预测误差对电网安全运行影响评价方法研究)

TM732

A

2096-3203(2017)01-0034-05