混合直流双桥换相失败机理及抑制措施研究

李 猛， 夏成军， 杜兆斌

(华南理工大学电力学院，广东 广州 510641)

混合直流双桥换相失败机理及抑制措施研究

李 猛， 夏成军， 杜兆斌

(华南理工大学电力学院，广东 广州 510641)

随着高压直流(HVDC)输电技术的发展，混合直流输电已经成为一种趋势。分析了逆变侧交流三相故障造成混合双馈入直流中电网换相换流器高压直流(LCC-HVDC)双桥换相失败的机理，区别了造成双桥连续换相失败与双桥非连续换相失败的主要影响因素。通过对LCC-HVDC在不同交流故障程度及故障触发时刻下仿真分析，研究了这2个因素对换相失败类型的影响，并发现交流系统轻微故障下的电压波形畸变是双桥非连续换相失败现象的主要成因。通过单纯形算法对混合双馈入系统中电压源换相换流器高压直流(VSC-HVDC)控制参数进行优化，抑制了在交流系统轻微故障情况下发生的LCC-HVDC双桥非连续换相失败。

混合直流；双桥换相失败；波形畸变；单纯形算法

随着高压直流输电工程在大容量远距离输电及区域电网互联等领域的广泛应用，将会出现两回或多回直流线路落点于同一交流系统的情况，形成多馈入直流输电系统[1-9]。当其中一回或多回直流为VSC-HVDC时，就会形成混合多馈入直流，这使得通过优化混合多馈入直流中VSC-HVDC的控制来抑制由交流系统故障造成的LCC-HVDC系统换相失败的发生成为可能。

现有对多馈入换相失败的研究多局限于仅含LCC-HVDC的传统多馈入直流，较少考虑含VSC-HVDC的混合多馈入直流。文献[5]中发现了双馈入直流系统中随着本地换流母线故障水平的提升，远端换流站换相失败的概率先增加后减少，然后再增加的异常现象。这种异常换相失败的原因被认为是轻微故障下电压波形畸变更为严重，过零点位移较多，更易造成双回直流换相失败。文献[6]在文献[5]的基础上，通过对3种典型故障水平下换流母线电压波形的对比，以及对故障后一个周期内B相电压进行傅立叶分析，指出低故障水平下电压波形中含有较大的直流分量和低次谐波是造成该种异常换相失败的主要原因。文献[5，6]虽然对双馈入直流中异常换相失败的影响因素及产生机理进行了分析，并没有给出抑制这种异常换相失败现象的方法。文献[10]在传统双馈入直流系统中引入了静止同步补偿器，并研究了其在改善双馈入直流系统稳态和暂态运行特性上的作用。文献[11，12]通过仿真分析，明确了混合双馈入系统中VSC-HVDC可以等效地增加系统的有效短路比，减少LCC-HVDC发生换相失败的几率，但只是分析了混合双馈入情况下VSC-HVDC固有特性对LCC-HVDC换相失败免疫因子的影响，没有进一步对如何优化VSC-HVDC控制或者二者间的协调控制来降低LCC-HVDC换相失败的概率进行研究。

现有的高压直流输电工程绝大多数采用单极12脉波换流器，12脉波换流器发生单、双桥换相失败对系统造成的冲击也不相同。发生双桥换相失败后，所在极的直流系统功率的传输中断，直流电流的爬升会更剧烈，设备承受的应力也会更大，这进一步影响了系统恢复稳态的速率；而只发生单桥换相失败的情况下，直流功率的传输不会中断，直流电流的上升也不如双桥换相失败来得剧烈，直流系统能够更快地恢复到稳态时的功率传输，从而减小故障对交直流系统带来的影响。现有文献中对于换相失败研究的精细化程度有所欠缺，都是以整个换流器为研究对象，未能精确到对单桥换相失败的研究。本文将双桥12脉波换流器发生换相失败分为Y桥单桥换相失败、D桥单桥换相失败、双桥非连续换相失败、双桥连续换相失败几个类型。分析了12脉动LCC-HVDC在逆变侧交流系统三相故障下的双桥换相失败机理，搭建了混合双馈入直流模型，结合仿真数据，分析了故障水平、故障时刻对LCC-HVDC换相失败类型的影响，以及故障过程中VSC-HVDC的控制策略及响应特性。仿真过程中发现在接地阻值较大时，LCC换流器会发生双桥非连续换相失败，随着接地电阻的减小，反而只发生单桥换相失败的异常现象，并对此作出解释。通过单纯形算法对VSC-HVDC控制参数进行优化，抑制了该种异常换相失败现象的发生。

1 双桥换相失败的机理分析

混合双馈入直流拓扑结构如图1所示，交流母线额定电压为525 kV，LCC-HVDC和VSC-HVDC的额定传输功率都是1000 MW，其中LCC-HVDC采用双桥12脉波换流器，换流变接线方式为YN/y0/d11，即Y桥阀侧电压滞后D桥阀侧电压30°相位角。

图1 混合双馈入直流拓扑结构

1.1 交流三相故障下的LCC-HVDC双桥换相失败机理

当逆变侧交流系统发生三相故障时，根据故障严重程度的不同，含有双桥换流器的直流系统可能会发生单桥换相失败、双桥换相失败，也可能不发生换相失败。双桥换相失败主要有2种情况，一是双桥非连续换相失败，二是双桥连续换相失败(本文认为Y桥和D桥在约2个ms内相继发生换相失败便可认为双桥连续换相失败，这是因为12脉波双桥换流器相邻导通顺序的2个阀触发脉冲的间隔为30°)。

假设某一故障程度下，如图1中所示的LCC-HVDC逆变侧双桥换流器中的Y桥发生单桥换相失败，而D桥恰好不发生换相失败。在故障发生前，D桥正常换相过程，以阀V2D向阀V4D换相为例，有(1)、(2)式成立。式中ua，uc分别为交流母线a、c相电压；Xr为交流系统(含换流变压器)每相等值电抗；Rr为交流系统每相等值电阻；i2D和i4D分别为流过阀V2D和V4D的电流，ID为直流电流。

(1)

i2D+i4D=Id

(2)

将(2)式代入(1)式，忽略交流系统等值电阻可得：

(3)

对(3)式左右两边同时积分可得：

(4)

可进一步化为：

(5)

式中：Acr为阀在正常工况下完成换相所需的临界换相电压时间面积；ul为额定工况下逆变侧交流母线电压有效值；α为触发延迟角；γ为熄弧角。当逆变侧交流三相故障发生后，交流电压有效值跌落至ul′，逆变站发生Y桥单桥换相失败，单极直流电压下降剧烈，虽然整流侧定电流控制会增大触发延迟角，逆变侧进入定熄弧角控制，减少触发延迟角至α′，但直流电流仍会不可抑制地上升，待关断的阀所需的换相时间面积增大。当阀完成换相所需的电压时间面积Acr大于换流器所能提供的最大换相电压时间面积Amax时，另一个换流桥D桥也会发生换相失败。因为有该故障程度下刚好不发生双桥换相失败的假设在前，即在直流电流达到最大值Id′，D桥逆变器熄弧角为刚好不会发生换相失败的最小值γmin。直流电流在峰值处附近的变化率dId/dωt可近似认为等于0，所以直流电流峰值处附近的D桥阀换相过程有式(6)成立：

(6)

令(4)、(6)两式等号两边相减，利用定积分的区间可加性可得:

(7)

上式可进一步化简为:

(8)

将式(5)带入式(8)，可得:

(9)

其中:Δul=ul-ul′，ΔId=Id′-Id，Δul/ul为交流系统发生三相故障，考虑单桥换相失败后直流电流增长而恰好躲过双桥换相失败的临界交流电压跌落百分比。

由式(9)可知，双桥非连续换相失败中第二个换流桥发生换相失败主要是由直流电流增大主导的。因为单桥换相失败后，直流电流的增大将导致临界交流电压跌落百分比的进一步下降。

如果故障程度较轻微，换相电压跌落较少，即便单桥换相失败后直流电流增大到峰值，由于控制系统的迅速响应以及换相裕度的存在(α→α′,γ→γmin)，直流系统也可能躲过双桥换相失败，只发生单桥换相失败。

然而在故障程度更为严重的情况下，由于换相电压的幅值跌落过大，导致换流桥能提供换相电压时间面积迅速减少至小于临界换相电压时间面积(由额定直流电流决定)，还未等到直流电流的陡增，Y桥和D桥便在很短的时候内相继发生换相失败，即视为发生了双桥连续换相失败。

1.2 交流三相故障下的VSC-HVDC暂态控制策略 交流故障发生时，VSC-HVDC利用换流器的快速响应能力，采取特殊的低电压穿越或电压变化率控制逻辑，有利于提升系统的故障穿越能力。

如图2所示，当VSC-HVDC检测到交流系统正序电压模值持续低于0.85 p.u.一段时间，或正序电压模值变化率在连续几个毫秒内都超过了门槛值，VSC-HVDC进入低电压穿越或电压变化率穿越逻辑，其外环控制器从稳态无功功率外环控制转为暂态交流电压外环控制，以增大无功电流输出，提升对换相电压的支撑作用[14]。

图2 VSC交流故障期间的外环控制策略

由于交流母线正序电压模值的计算过程中,正序电压的d、q轴分量取1/4个周期内的平均值，因此故障过后的5个ms内正序模值的计算存在一定误差，这可能会导致柔性直流控制响应的延迟。

2 混合双馈入系统中LCC-HVDC换相失败的仿真分析

在PSCAD/EMTDC中搭建如图1所示的混合双馈入直流输电模型，对逆变侧交流系统设置不同接地阻值(从285 Ω到0 Ω)的交流三相接地故障，同时改变故障触发时刻(从8.100 s到8.109 s)。试验结果如图3所示，可知随着接地阻值的减小(故障水平的上升)，换流器换相失败类型基本呈现出愈来愈严重的趋势，符合1.1节中关于换相失败的机理分析。但式(9)忽略了故障触发时刻的影响，仅适用于故障触发时还未导通，故障后才开始导通的阀换相过程，不适用于故障触发于换相过程中的情形，下面进一步分析换相失败类型同故障时刻的关系。

图3 不同交流故障下换相失败类型统计

2.1 故障时刻对换相失败类型的影响

在同一接地阻值下，不同故障时刻下可能会发生单桥换相失败、双桥换相失败(包括双桥非连续换相失败和双桥连续换相失败)，也可能不发生换相失败。若故障发生在阀换相过程中，且对应的角度为ωt，由于换相时间较短且假设此时换流器恰好能躲过换相失败，则直流电流在该阀换相过程中的变化可以忽略，易推知:

(10)

式(10)和式(4)相减得：

(11)

进一步化简可得:

(12)

由于α<ωt<π-γmin，所以临界交流电压跌落百分比会随着ωt的增大而增大。下面分别以8.104 s，8.105 s触发接地阻值为210 Ω的三相故障为例，分析故障时刻对换相失败的影响。

2.1.1 8.104 s触发接地阻值为210 Ω的三相故障

如图4所示，8.104 s时在逆变侧交流系统触发三相接地故障。此时，阀V6D处于换相过程的开始阶段，V6D刚刚导通不久。对应于式(12)，即ωt非常接近于α，由于Δul/ul在α<ωt<π-γmin范围内单调递增，即故障的发生对V6D承受交流电压跌落而不发生换相失败的能力影响显著，D桥发生换相失败。

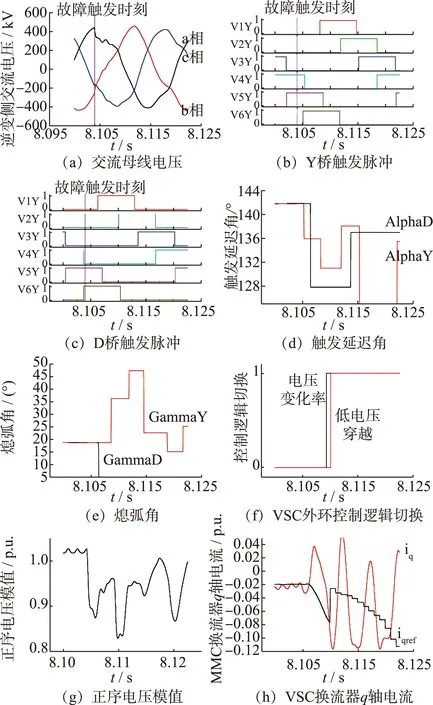
图4 交流故障后混合双馈入直流系统响应(8.104 s触发)

当V6Y导通时，由图4(d)可知直流控制系统已经响应，Y桥换流器的触发延迟角减小至约136°，虽然在该阀换相过程中，交流电压一直处于故障水平，但是由于积分区间的增大，换相时间面积得以增大，从而躲过双桥换相失败。

观察图4(f)、(g)、(h)可知，虽然故障于8.104 s就已触发，由于1.2节所述的正序电压模值检测误差问题的存在，VSC-HVDC经过约5个ms，直到约8.109 s才进入电压变化率控制，而之前由稳态无功功率外环控制产生的iqref被清掉，VSC-HVDC进入暂态交流电压环控制，iqref的爬坡速度较慢，无功电流在故障初期的响应十分有限。

2.1.2 8.105 s触发接地阻值为210 Ω的三相故障

如图5所示，8.105 s时在逆变侧交流系统触发三相接地故障。此时，阀V6D处于换相过程的最后阶段。对应于式(12)，即ωt非常接近于π-γmin，由于Δul/ul在α<ωt<π-γmin范围内单调递增，即故障的发生对V6D承受交流电压跌落而不发生换相失败的能力没有显著影响，D桥无换相失败发生。

同时，由于故障触发时刻在V6Y开始换相之前，且由图5(d)可知，此时直流控制系统还未来得及做出响应，Y桥换流器的触发延迟角仍为α。对应于式(12)，即ωt=α，此时故障的发生对V6Y承受交流电压跌落而不发生换相失败的能力影响最大，Y桥发生换相失败

同样，VSC-HVDC在故障初期响应有限，对换流电压的支撑作用不明显，存在一定优化空间。

由上述2个案例可知，故障触发时刻以及直流控制系统的响应速度会对换相失败类型产生影响。

2.2 异常换相失败分析

观察图6，在轻微交流三相故障下(接地阻值为255 Ω)，逆变侧发生双桥非连续换相失败，而接地阻值减小至210 Ω时，逆变侧只发生单桥换相失败。

在8.104 s时设置接地阻值为210 Ω的三相接地故障，观察图6(b)、(d)可知，换流器只发生了D桥换相失败，直流电流只有一处波峰。在8.104 s时设置接地阻值为255 Ω的三相接地故障，观察图6(a)、(c)可知，D桥换相失败先发生，间隔了约13个ms，在直流电流上升到第一个波峰处附近，又发生了Y桥换相失败，直流电流也发生了第二次陡升。

观察如图7所示的逆变侧换相电压波形，在发生接地阻值为255 Ω的三相接地故障时，换相电压过零点较发生接地阻值为210 Ω的三相接地故障时提前。以B相电压为例，分别选取2种故障后一个周波内的逆变侧交流电压做傅立叶变化，进行谐波分析，得到图8。

通过对比可以发现，在接地阻值为255 Ω时，b相电压的各次谐波含量均高于接地阻值为210 Ω的情况，这种差别尤其体现在直流分量和2次、3次等低次谐波上，这导致交流电压在接地阻值为255 Ω时波形畸变程度大于接地阻值为210 Ω时，从而导致了换相电压过零点的前移。由式(6)可知，尽管交流电压跌落百分比在接地阻值为255 Ω时小于接地阻值为210 Ω的情况，但由于换相电压过零点的前移，积分的时间区间相对减小，所以系统能够提供的不发生换相失败的最大换相电压时间面积也相应减小。而由于之前单桥换相失败已经发生，造成直流电流不可抑制的上升，阀完成换相所需的电压时间面积相应增大，导致了后续双桥换相失败的发生。

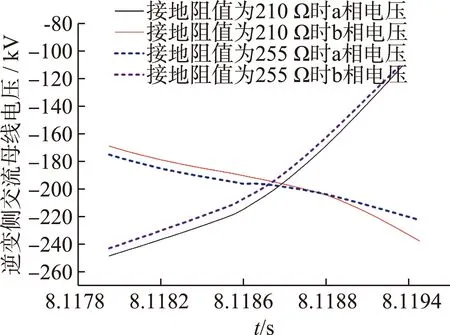
图7 不同交流故障下的换相电压

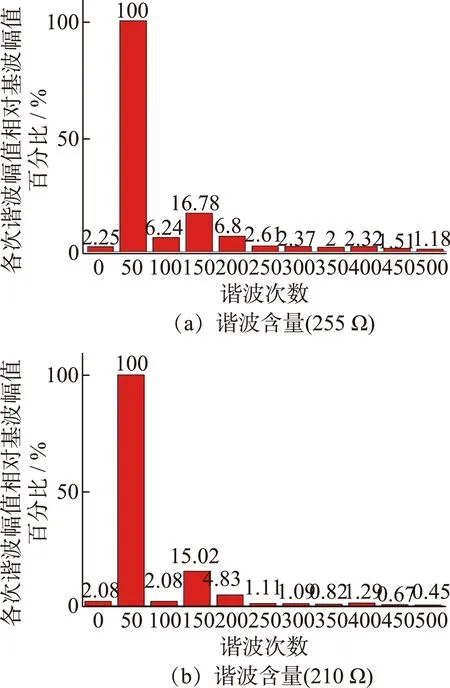
图8 不同交流故障下的交流电压谐波含量

3 异常换相失败的抑制措施

由1.2节可知，故障情况下VSC-HVDC进入暂态控制逻辑(低电压穿越控制或电压变化率控制)，其外环控制器由稳态无功功率外环控制切换暂态交流电压外环控制，但从2.1节仿真分析可知，现有的控制参数下，故障初期VSC-HVDC对换相电压的支撑作用有限。暂态交流电压外环控制根据给定的暂态交流电压参考值Vreftran计算得到无功电流参考值iqref，再送给内外电流控制器进行控制，因此可以考虑通过改变Vreftran的大小来增大无功电流的输出，改善故障初期VSC-HVDC对换流电压的支撑作用，以求减少换相失败的发生或降低换相失败的严重程度。采用单纯形算法，可以对参数Vreftran寻优，使得在优化的控制参数下，逆变侧轻微故障时只发生单桥换相失败而不发生异常的双桥非连续换相失败。

3.1 单纯形算法

单纯形算法是一种基于几何形状考虑的启发式优化算法，所谓单纯形指的是在n维空间中，以n+1个端点构成的最简单图形。该算法在初始单纯形的每个顶点对目标函数进行计算，舍弃掉结果最大的端点，并以其余端点的几何中心为中点找到被舍弃端点的镜像作为新的端点，然后在新的单纯形上重复上面的步骤，以不断逼近更小的目标函数值。

设置优化的目标函数为：

(13)

其中Ud为测量得到的直流电压的标幺值;Id为测量得到的直流电流标幺值;t为三相故障触发时刻，故障后经T时间，直流系统重新恢复到稳定状态。

设置于8.100 s触发的接地阻值为255 Ω的交流三相故障，令暂态无功电压外环控制的参考值初值Vreftran为1，利用单纯形算法经过10次运算，得到优化后的参数Vreftran为1.087 5。

3.2 参数优化前后的波形对比

观察图9，通过对比分析参数优化前后的直流电流、交流线电压、无功电流波形可知，优化前直流电流有2个波峰，分别对应于D桥、Y桥换相失败，且直流电流升到峰值处后一直跌至0，即直流功率的传输中断，直到8.216 s直流电流才恢复到稳态时的90%；优化后直流电流的波峰减为1个，对应与换流器D桥换相失败，并无Y桥换相失败的发生，且直流电流最低时仍大于0.5 p.u.，直流功率的传输没有中断，到8.154 s直流电流已经恢复到稳态时的90%，较之优化前提前了约3个周波的时间。

同时优化后无功电流在故障初期较之优化前有明显增长，使得逆变侧交流电压获得一定程度的抬升。优化后无功电流在8.140 s附近时有明显的回落，这是因为控制系统检测到逆变侧电压恢复到一定程度并持续指定时间后，VSC-HVDC逆变侧由暂态无功电压外环控制切换回稳态无功外环控制，同时防止了逆变侧过电压情况的出现。

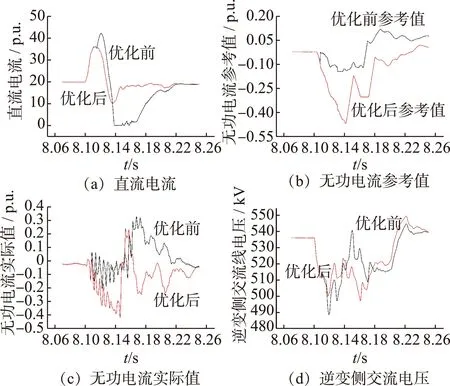
图9 优化前后混合双馈入直流系统响应

4 结束语

本文分析了LCC-HVDC发生单桥换相失败、双桥换相失败的机理，指出单桥换相失败后直流电流上升的快慢是导致双桥非连续换相失败发生与否的主要原因，双桥连续换相失败则主要归因于换相电压的大幅跌落。通过对不同交流故障时刻、不同故障程度下的仿真数据进行分析，阐明了故障时刻与故障程度对换流器换相失败类型的影响，同时解释了交流系统轻微程度故障下换流器发生双桥非连续换相失败而一般程度故障下只发生单桥换相失败的原因是轻微交流故障下，接地阻值更大，系统的戴维南等效阻抗更大，短路比更小，波形畸变也更为严重。通过单纯形算法对混合双馈入系统中的VSC-HVDC参数进行优化，可以有效抑制这种异常换相失败情况的发生，有利于直流系统的快速恢复，减小故障对交直流系统的影响。

[1] 林凌雪, 张 尧, 钟 庆, 等. 多馈入直流输电系统中换相失败研究综述[J]. 电网技术,2006,30(17): 40-46.[2] 赵利刚, 赵 勇, 洪 潮, 等. 基于实际录波的南方电网多回直流换相失败分析[J]. 南方电网技术,2014,8(4): 42-46.[3] 王 珂, 杨卫东, 方勇杰, 等. 有利于多馈入直流输电系统协调恢复的VDCOL控制策略研究[J]. 江苏电机工程,2007,26(1): 1-4.

[4] 吴 萍, 林伟芳, 孙华东, 等. 多馈入直流输电系统换相失败机制及特性[J]. 电网技术,2012,36(5): 269-274.

[5] RAHIMI E，GOLE A M，DAVIES J B，et al. Commutation Failure Analysis in Multi-infeed HVDC Systems[J]. IEEE Trans on Power Delivery,2011,26(1): 378-384.

[6] 赵 彤, 吕明超, 娄 杰, 等. 多馈入高压直流输电系统的异常换相失败研究[J]. 电网技术,2015,39(3): 705-711.

[7] 肖 浩, 朱 佳, 李银红, 等. 多馈入直流系统换相失败免疫水平快速确定方法研究[J]. 中国电机工程学报,2015, 35(11): 2711-2717.

[8] 李新年, 刘 耀, 朱艺颖, 等. 华北电网直流多馈入系统动态特性实时仿真[J]. 电网技术,2011,35(8): 75-80.

[9] 李新年, 陈树勇, 庞广恒, 等. 华东多直流馈入系统换相失败预防和自动恢复能力的优化[J]. 电力系统自动化,2015,39(6): 134-140.

[10] 郭春义, 张岩坡, 赵成勇, 等. STATCOM对双馈入直流系统运行特性的影响[J]. 中国电机工程学报,2013,33(25): 99-106.

[11] 倪晓军, 赵成勇, 郭春义, 等. 混合双馈入直流系统中VSC-HVDC对LCC-HVDC受端系统强度的影响[J]. 中国电机工程学报,2015,35(16): 4052-4061.

[12] 徐 岩, 刘泽锴, 应璐曼. 含VSC-HVDC的混合MIDC系统强度计算及仿真分析[J]. 华北电力大学学报(自然科学版),2015,42(2): 30-35.

李 猛

李 猛(1991 —)，男，安徽阜阳人，硕士研究生，研究方向为高压直流输电；

夏成军(1974 —)，男，湖北黄冈人，博士，副教授，研究方向为电力系统分析运行与控制、HVDC与FACTS；

杜兆斌(1977 —)，男，广东佛山人，博士，讲师，研究方向为电力系统稳定性分析与控制。

Research on the Mechanism and Suppression Method of Double Bridge Discontinuous Commutation Failure in Hybrid HVDC

LI Meng, XIA Chengjun, DU Zhaobin

(School of Electric Power, South China University of Technology, Guangzhou 510641, China)

With the development of high voltage direct current(HVDC) transmission technology, hybrid multi-infeed direct current transmission become a development trend. The mechanism of double bridge commutation failure of line commutated converter based high voltage direct current (LCC-HVDC) in hybrid double-infeed system is analysized. And the major influence factors of double bridge continuous and discontinuous commutation failure are distinguished. Through simulation under different AC system fault extent and trigger time, the effect of these two factors on commutation failure types is studied, and it is found that the AC voltage waveform distortion under slight fault is the main cause of double bridge discontinuous commutation failure. Then the control parameter of voltage source converter based high voltage direct current(VSC-HVDC) is optimized by Simplex algorithm to suppress double bridge discontinuous commutation failure of LCC-HVDC in slight fault.

hybrid HVDC; double bridge commutation failure; waveform distortion; Simplex algorithm

2016-10-26；

2016-11-25

国家自然科学基金(51577071)；广东省自然科学基金(2015 A030313202)

TM721

A

2096-3203(2017)01-0047-06