结合PSO的改进压缩跟踪方法

刘韶涛， 姚灿荣

(华侨大学 计算机科学与技术学院， 福建 厦门 361021)

结合PSO的改进压缩跟踪方法

刘韶涛， 姚灿荣

(华侨大学 计算机科学与技术学院， 福建 厦门 361021)

针对基于在线检测的跟踪方法中目标在多尺度空间中的搜索和匹配问题，结合粒子群优化算法(PSO)和压缩感知思想，提出一种鲁棒的多尺度目标跟踪算法.首先,通过粒子群在多尺度空间中采集样本;然后,经过压缩感知提取特征;最后,通过粒子的迭代计算，搜索出当前目标的最佳匹配位置.实验结果表明：提出的算法能较好地适应目标的多尺度变化，在快速性和鲁棒性上具有更好的性能. 关键词： 目标跟踪; 压缩感知; 粒子群优化; 多尺度

一个典型的目标跟踪系统包括表观模型和在当前帧定位目标新位置的搜索策略[1].由于光照变化、遮挡等问题，导致目标的表观模型时常发生变化.因此，一个自适应强的表观模型表示对鲁棒的目标跟踪十分重要.基于特征实时检测[2-3]的运动目标跟踪方法是近年来的一种主流目标跟踪技术[4-6].在线方法在对目标进行分类判别的同时，也在对图像进行采样，用于实时更新分类器，使检测器具有一定的适应能力，不仅在一定程度上解决了检测和跟踪时的遮挡问题，还能适应复杂场景下的多目标跟踪.然而，其计算和搜索复杂度较高，且容易产生漂移.近年来，基于随机优化技术的粒子群优化算法(PSO)被广泛应用于计算机视觉处理[7-9].为了在多尺度空间中快速寻找目标，降低计算代价，保持跟踪的实时性和重叠率，本文提出一种结合粒子群优化的压缩跟踪算法(PSO-CT)，在每一帧的目标搜索过程中，利用粒子群优化的搜索方法，在多尺度空间中更快速地搜索目标.

1 压缩跟踪算法

压缩跟踪(compress tracking)算法是Zhang等[6]基于压缩感知理论[10]提出的一种高效、快速的基于在线学习的实时跟踪方法.压缩跟踪算法的流程，如图1所示.图1中：分类器更新是通过在当前帧跟踪结果的邻域内采集正负样本，然后进行压缩，训练分类器得到.

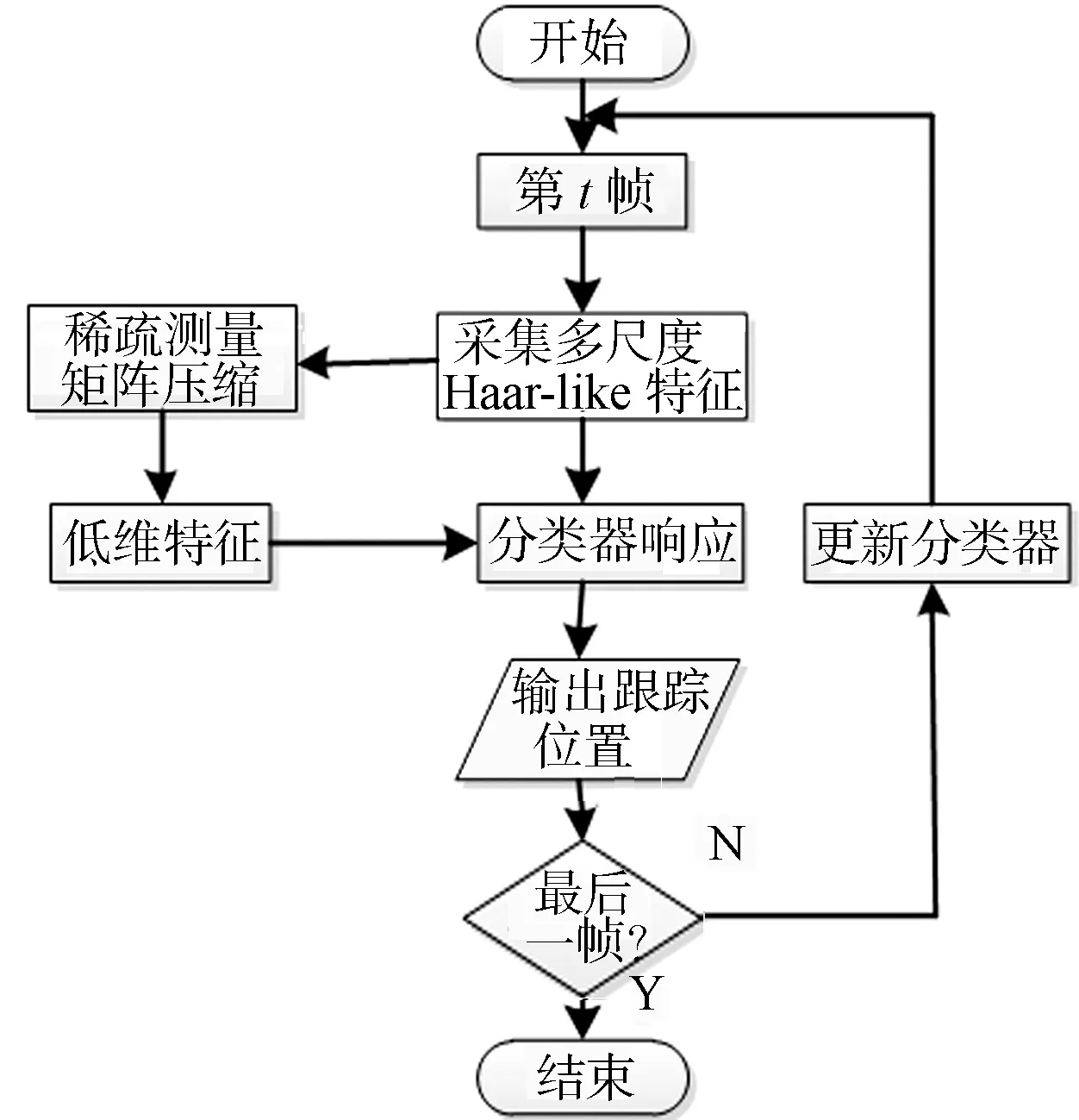
图1 实时压缩跟踪算法流程Fig.1 Real-time compress tracking algorithm

1.1 随机投影

图2 特征映射Fig.2 Feature projection

如果信号通过某种变换后是可稀疏表示或者可压缩的，则可以设计一个与变换基不相关的测量矩阵来测量信号，得到的测量值通过求解优化问题可实现信号的精确或者近似重构.具体地，对于高维图像空间中的数据x∈Z，如果x在正交基Ψ上是K-稀疏的，且能找到一个与Ψ不相关的观测基R，则可以使用随机观测矩阵R∈Zn×m，将其投影到低维空间y∈Zn上，如图2 所示.图2中：n≪m.Johnson-Lindenstrauss准则表明：当随机测量矩阵R满足有限等距性质时，K个系数可通过求解最小误差，从y中高概率地恢复原始信号x.

1.2 随机测量矩阵

为了适应实际应用的实时性需求，采用文献[6]提出的一个非常稀疏的随机测量矩阵，具体矩阵元素定义为

(1)

式(1)中:p为随机元素ri，j取某个值的概率.例如，取s=n/4时,测量矩阵非常稀疏，即n行中每行只需2～4个非零元素，就能满足Johnson-Lindenstrauss推论，且只需初始的一次离线计算就能满足整个跟踪过程的计算．

假设s是第t-1跟踪到的目标位置，在以s为中心,r为半径的范围内，采集测试样本集的Haar-like特征：Ti∈Zw×h×l(i=1,2,…,r2)，l为Haar-like的模板数，则每个特征的维数m可能达到106以上.利用初始产生的随机稀疏矩阵,将此高维数据投影到低维空间中，形成适合快速计算的低维特征v.

图3 图像特征的多尺度表示Fig.3 Representation of multi-scale feature

1.3 目标的Haar-like多尺度表示与尺度不变性

(2)

2 基于PSO改进的压缩跟踪算法

2.1 粒子群优化算法

图4 粒子更新示意图Fig.4 Particle update schematic

(3)

(4)

式(3)，(4)中:ω为迭代权重；φ1，φ2为大于0的常数，用于平衡个体最佳和全局最佳；r1,r2∈(0,1)为均匀分布的随机数.

2.2 结合PSO改进的压缩跟踪

(5)

式(5)中:Σ为高斯矩阵的协方差.

对角线元素为速度预测，即

(6)

2.3 适应值函数

在当前帧，以前一帧为中心，半径R(足够大)的圆，或者为边长的正方形范围内，按高斯分布随机初始化K个粒子.由于在前一帧中已经更新了分类器，因此,用分类器的分类响应作为粒子j在第t次迭代时相应的适应函数值,即

(7)

式(7)中:zj,t为粒子xj,t在当前位置时提取的低维特征向量.

根据每个粒子的适应函数值f(xj,t)，得到全局最佳g和粒子j的个体最佳pt,j的更新，即

(8)

(9)

(10)

(11)

(12)

由式(10)～(12)可知：通过适应函数值可以控制个体和社会认知的变化，使之得到平稳控制，而粒子最大速度可利用先验知识获取.

2.4 分类器更新

当获取当前帧的最大响应位置时，确定目标在当前帧的位置.为了确定正负样本的采样范围，通过2个距离阈值α和β来界定采样的类别.在Dα= {z|||l(z)-lt||<α}区域内采集正样本，在区域Dζ,β={z|ζ<||l(z)-lt||<β}采集负样本.其中，α<ζ<β，即靠近当前目标中心的随机采集为正样本，外围采集为负样本.

根据正负样本，分类器的参数更新为

(13)

(14)

当目标在场景中因转向、形变、遮挡及镜头晃动等因素发生剧烈变化时，可能导致粒子在给定范围内的适应值无法小于阈值，搜索终止于局部最优.结合文献[12]的方法，采用选择更新和re-search策略.当目标发生遮挡时，分类器的响应值显著减小，为了不被遮挡物完全取代，设定一个分类阈值TC；当分类相应低于阈值时，分类器停止更新；当在给定的局部范围内无法搜索到目标时，则跳出局部搜索范围，增加粒子数量，将PSO搜索范围扩大至全局搜索.

PSO-CT算法有以下5个步骤.

步骤1 初始化粒子群参数、分类器和目标特征.

步骤2 对于每一帧，有如下5点：

1) 计算Frame(t)的积分图；

2) 如果第t-1帧的分类响应P>TC，则对于每个目标，根据上一帧得到的目标位置，在以上一帧的目标为中心，d为边长的正方形内随机产生K个粒子，并初始化个体最佳pj和全局最佳g；否则，在全局范围内，将尺度参数w，h范围扩大，随机产生4K个粒子，并初始化4K个例子的个体最佳pj和全局最佳g；

3) 计算每个粒子的Haar-like特征，计算粒子的分类得分，得到各自的适应值f(x(j,t))；

4) 比较f(x(j,t))及pj和g，更新个体最佳pj和全局最佳g,修改粒子的位置和速度；

5) 如果f(g) 满足搜索结束条件，则得到这一帧的目标位置:Loc=g；否则，跳转至全局搜索2).

步骤3 在跟踪到的当前帧目标周围Xζ,β={x|ζ<||It+1(x)-It(x*)||<β}，采集正、负样本.

步骤4 利用上面的积分图，计算正样本和负样本的Haar-like特征值，压缩特征.

步骤5 通过正样本和负样本更新分类器，进行下一帧处理.

3 结果与分析

3.1 粒子数的确定

为了验证算法的有效性，在CPU主频为3GHz，内存为8GB的PC实验环境下，采用几个标准视频集[13]，将文中算法与粒子滤波(PF)、基于检测学习跟踪算法(TLD)、压缩跟踪算法(CT)进行比较.

(a) 中心平均定位误差 (b) 帧平均处理时间图5 粒子数与平均定位误差和帧平均处理时间Fig.5 Particle number， CLE and PT

为了更好确定实验中粒子个数，针对粒子数与算法性能的关系进行多次重复实验，结果如图5所示.

图5中：n1为粒子数；t为帧处理时间.由图5可知：如要实现实时跟踪，必须合理控制粒子数量.其中，中心定位误差(CLE)的计算为

(15)

式(15)中：(xt,yt)和(xr,yr)分别表示当前跟踪定位结果与人工定位标准位置.

图6 粒子平均迭代次数Fig.6 Average iteration times of particle

3.2 PSO-CT的跟踪性能分析

将粒子数设置为30，将收敛阈值Th=0.01,Tc=0.6，迭代参数ω=0.5，初始φ1=0.5，φ2=0.5，最大迭代次数设为100.设4维搜索空间半径为40.在测试粒子搜索目标过程中，计算复杂度的实验结果，如图6所示.PSO-CT平均每个粒子的迭代次数(n2)为42.4 次·帧-1，总迭代次数为30×42.4，相当于只需1 272次搜索和比对，就能在每一帧图像中发现目标.文献[6]采用改进全搜索的coarse-to-fine策略需要3 496次.在几组复杂场景下的跟踪结果，如图7,8所示，其帧率如表1所示.图8中：n3为帧数；e为跟踪误差.

(a) David第160帧 (b) David第182帧 (c) David第292帧

(c) Car第88帧 (d) Car第252帧 (e) Car第621帧

(f) Carcase第67帧 (g) Carcase第115帧 (h) Carcase第849帧图7 复杂环境下几种跟踪算法结果Fig.7 Tracking result of some algorithm in complex scenes

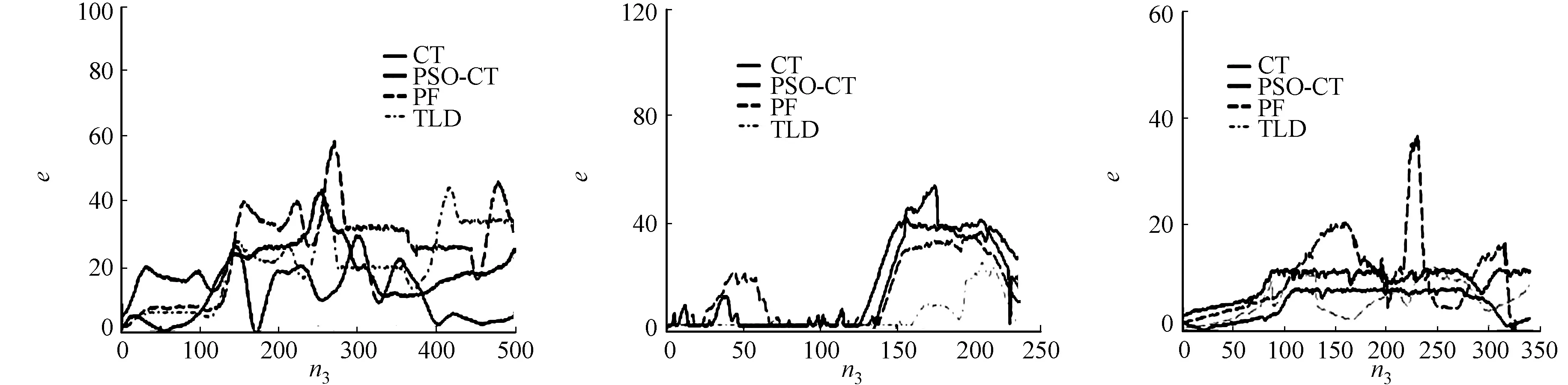
(a) Motocross (b) Mountainbike (c) Coke图8 几种算法的跟踪误差Fig.8 Tracking error of some algorithms

由图8可知：Motocross中目标因为翻转产生平稳形变,此时，TLD算法、PF算法和PSO-CT算法表现出良好效果;Mountainbike中场景从平稳跨越到剧烈抖动，此时，原始PSO-CT算法在平稳环境误差较小，而面对突变，最终也能快速校正偏差;Coke场景中，中间经历几次遮挡和高度变化，当镜头或者景深发生明显变化时，多尺度的PSO-CT的尺度适应性能优势明显.

表1 几种跟踪算法的平均帧率Tab.1 Average frame processing rate of some tracking algorithms

综上可知，在变化比较快的复杂场景下，CT和PSO-CT表现相对稳定，且PSO-CT能适应突然、快速的目标位置变化.当镜头或者景深发生明显变化时，多尺度的PSO-CT在尺度变化的自适应方面体现出良好的跟踪效果.在时间效率上，如表1所示.由于采用特征压缩方法，将特征用低维的向量表示，CT算法和PSO-CT算法在速度上具有优势，体现出良好的快速性和实时性.

4 结束语

针对原始压缩跟踪存在的不足，结合粒子群优化算法的优化多维空间搜索，实现复杂场景下多尺度目标跟踪.实验表明，提出的PSO-CT跟踪方法在实时性和稳定性上具有一定优势.该算法对运动目标发生部分遮挡和形变时仍然有较好的鲁棒性，然而，当多个目标之间产生聚合与分离时，跟踪还达不到最理想的结果，这将是下一步工作需要考虑和突破的地方.

[1] 龚声蓉,刘纯平,季怡.复杂场景下图像与视频分析[M].北京:人民邮电出版社,2013:8-9.

[2] KALAL Z,MIKOLAJCZYK K,MATAS J.Tracking-learning-detection[J].Pattern Analysis and Machine Intelligence,2012,34(7):1409-1422.

[3] STALDER S,GRABNER H,GOOL L V.Cascaded confidence filtering for improved tracking-by-detection[M].Berlin:Springer,2010:369-382.

[4] GRABNER H,GRABNER M,BISCHOF H.Real-time tracking via on-line boosting[C]∥British Machine Vision Conference.Edinburgh：[s.n.]，2006:6.

[5] FELZENSZWALB P,MCALLESTER D,RAMANAN D.A discriminatively trained, multiscale, deformable part model[C]∥IEEE Conference on Computer Vision and Pattern Recognition.Anchorage:IEEE Press,2008:1-8.

[6] ZHANG Kaihua,ZHANG Lei,YANG M H.Real-time compressivetracking[C]∥Europeanence on Computer Vision.Berlin:Springer,2012:864-877.

[7] SAINI S,AWANG R D R,ZAKARIA M N B,etal.A review on particle swarm optimization algorithm and its variants to human motion tracking[J].Mathematical Problems in Engineering,2014(2014):1-16.

[8] ZHANG Xiaoqin, HU Weiming, MAYBANK S,etal. Sequential particle swarm optimization for visual tracking[C]∥IEEE Conference on Computer Vision and Pattern Recognition.Anchorage:IEEE Press,2008:921-928.

[9] FLEISCHMANN P,AUSTVOLL I,KWOLEK B.Particle swarm optimization with soft search space partitioning for video-based markerless pose tracking[J].Lecture Notes in Computer Science,2012,7517:479-490.

[10] BARANIUK R.Compressive sensing[J].IEEE signal processing magazine,2007,24(4):118-121.

[11] THIDA M,ENG H,MONEKOSSO D N,etal.A particle swarm optimisation algorithm with interactive swarms for tracking multiple targets[J].Applied Soft Computing,2013,13(6):3106-3117.

[12] TAWAB A M A,ABDELHALIM M B,HABIB S.Efficient multi-feature PSO for fast gray level object-tracking[J].Applied Soft Computing,2014,14(1):317-337.

[13] WU Yi,LIM J,YANG M H.Online object tracking: A benchmark[C]∥IEEE Conference on Computer vision and pattern recognition.Portland:IEEE Press,2013:2411-2418.

(责任编辑： 钱筠 英文审校： 吴逢铁)

Improved Compress Tracking Algorithm Based on PSO

LIU Shaotao， YAO Canrong

(College of Computer Science and Technology, Huaqiao University, Xiamen 361021, China)

For the searching and matching problem in multi-scale space of online detecting tracking method, a robust multi-scale tracking algorithm was proposed based on particle swarm optimization (PSO) and compress sensing. Firstly, feature was sampled with particles in multi-scale space. Then feature was extracted by compress sensing. Finally, targets would be searched quickly and robustly after calculate the best fitness and position of all the particle. The experimental results demonstrate that the proposed algorithm can adapt target in multi-scale change and has a better performance in robustness and rapidity. Keywords： visual tracking; compress sensing; particle swarm optimization; multi-scale

10.11830/ISSN.1000-5013.201701024

2015-06-02

刘韶涛(1969-)，男，副教授，主要从事软件体系结构的研究.E-mail:shaotaol@hqu.edu.cn.

国务院侨办科研基金资助项目(09QZR02)

TP 391.3

A

1000-5013(2017)01-0121-06