一类三阶三点边值问题正解的存在性

程德胜, 武晨

(江苏联合职业技术学院南京分院 基础课程教学部, 南京 江苏 210019)

一类三阶三点边值问题正解的存在性

程德胜, 武晨

(江苏联合职业技术学院南京分院 基础课程教学部, 南京 江苏 210019)

考虑一类三阶三点边值问题u‴(t)+a(t)f(u(t))=0,t∈(0,1),u(0)=u′(0)=0,u′(1)-αu′(η)=λ, 其中，0<η<1,0<α<1/η,λ>0,f满足超线性或者次线性条件，利用锥上的不动点定理，得到上述边值问题解的存在性结果.结果表明：文中方法进一步改进和推广了吴红萍的结果. 关键词： 三阶三点边值问题; 锥; 格林函数; 不动点定理

三阶微分方程边值问题是研究奇数阶边值问题的基础,由于其广泛的物理背景和现实意义，三阶边值问题引起了许多学者的关注，并且取得了较多成果[1-10]. 吴红萍[2]考虑了三阶三点边值问题u‴(t)+a(t)f(u(t))=0,t∈(0,1),u(0)=u′(0)=0,u′(1)-αu′(η)=λ.其中：0<η<1；0<α<1/η；λ>0.通过应用Leggett-Wilmlias不动点定理得到上述边值问题有3个正解的存在性.但作者仅考虑在上述条件下解的存在性，并没有考虑到当f满足超线性或次线性条件下,上述边值问题的解是否存在.本文研究一类三阶三点边值问题,即

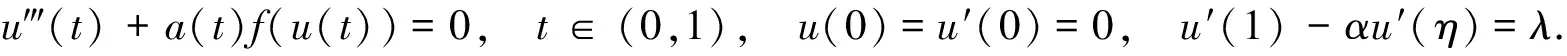
1 一些引理及定义

引理2[3]边值问题 u‴(t)+a(t)f(u(t))=0，t∈(0,1)，u(0)=u′(0)=0,u′(1)-αu′(η)=λ,有唯一解，即

(2)

引理4[3]对任意(t,s)∈[0,1]×[0,1]，有0≤G1(t,s)≤s(1-s).

(3)

由引理3可得

则有

(4)

当t∈[τ,1]时，由引理3和式(4),有

2 主要结果

定理1 假设f0=0，且f∞=∞(超线性)，则边值问题(1)至少存在一个正解.

证明 因为f0=0，所以存在R1>0，使0≤u≤R1时，有f(u)≤εu,t2≤ε‖u‖成立.其中，ε为大于0的常数，且满足

(5)

当u∈K,‖u‖=R1时，由引理3和式(5)，有

(6)

令Ω1={u∈E：‖u‖

另一方面，由f∞=∞可知，存在R2>R1，使u≥τ2R2时，有f(u)≥ρu成立.其中，ρ>0，且满足

(7)

令Ω2={u∈E：‖u‖

定理2 假设f0=∞，且f∞=0(次线性)，则边值问题(1)至少存在一个正解.

证明 因为f0=∞，则存在R3>0，使0≤u≤R3时，有f(u)≥δu成立.其中，δ>0，且满足

(8)

当u∈K,‖u‖=R3时，由式(8)可得

令Ω3={u∈E：‖u‖0，且满足

(9)

下面分两种情况进行讨论.

1) 如果f是有界的，即存在M>0，当u∈[0,+∞]时，有f(u)≤M成立，此时，令

从而‖Tu‖≤‖u‖.

因此,‖Tu‖≤‖u‖.无论哪一种情况，都可以令Ω4={u∈E：‖u‖

3 结束语

建立适当的格林函数，选择合适的锥，运用锥拉伸与压缩不动点定理，对一个含参数的三阶边值问题在满足超线性或者次线性条件下正解的存在性进行了探究，得到了一些新的推广的结果，也丰富了对锥拉伸压缩不动点定理的理论分析.

[1] 杨春风.一类三阶三点边值问题正解的存在性和不存在性[J],山东大学学报(理学版),2012,47(10):109-115.

[2] 吴红萍.一类三阶三点非齐次边值问题的两个正解[J].西北师范大学学报(自然科学版),2012,48(6):9-12.

[3]SUNYongping.Positivesolutionsforthird-orderthree-pointnonhomogeneousboundaryvalueproblems[J].ApplMathLetters,2009,22(1):45-51.

[4] 王全义,邹黄辉.一类n阶非线性三点边值问题单调正解的存在性[J].华侨大学学报(自然科学版),2014,35(3):344-348.

[5] 王全义,邹黄辉.非线性奇异三阶两点边值问题单调正解的存在性[J].华侨大学学报(自然科学版),2012,33(6):699-704.

[6] 高婷,韩晓玲.三阶无穷多点边值问题正解的存在性[J].四川大学学报(自然科学版),2016,53(1):35-41.

[7] 武晨.带有积分型边值条件的奇异的n阶边值问题无穷多正解的存在性[J].淮北师范大学学报(自然科学版),2015(3):14-17.

[8] 孙建平,张小丽.非线性三阶三点边值问题正解的存在性[J].西北师范大学学报(自然科学版),2012,48(3):1-4.

[9] 孙建平,彭俊国,郭丽君.非线性三阶三点边值问题的正解[J].兰州理工大学学报,2009,35(1):139-142.

[10] 吕学哲,裴明鹤.一类三阶三点边值问题正解的存在性[J].北华大学学报(自然科学版),2014(5):577-580.

(责任编辑： 钱筠 英文审校： 黄心中)

Existence of Positive Solution for Third-Order Three-Point Boundary Value Problems

CHENG Desheng, WU Chen

(Basic Courses Teaching Department， Branch of Nanjing Jiangsu Union Technical Institute, Nanjing 210019, China)

We study the existence of positive solution to the following third-order three-point boundary value problemsu‴(t)+a(t)f(u(t))=0，t∈(0,1)，u(0)=u′(0)=0,u′(1)-αu′(η)=λ, where 0<η<1, 0<α<1/η,λ>0. By using fixed point theorem in cones, we obtain the existence of the positive solution iffis either superlinear or sublinear. Our results extend and improve some results made by Wu Hongping. Keywords： third-order three-point boundary value problem; cone; Green fuction; fixed point theorem

10.11830/ISSN.1000-5013.201701025

2016-11-25

程德胜(1970-)，男，副教授，主要从事非线性泛函分析、课程论的研究.E-mail:cdsyycxr@sina.com.

国家自然科学基金资助项目(60773128)

O 175.8

A

1000-5013(2017)01-0127-04