变参数FOPDT型系统的强鲁棒自适应PI控制器设计

邵辉， 胡伟石， 洪雪梅， 罗继亮

(1. 华侨大学 信息科学与工程学院， 福建 厦门 361021;2. 华侨大学 实验室与设备管理处， 福建 厦门 361021)

变参数FOPDT型系统的强鲁棒自适应PI控制器设计

邵辉1， 胡伟石2， 洪雪梅1， 罗继亮1

(1. 华侨大学 信息科学与工程学院， 福建 厦门 361021;2. 华侨大学 实验室与设备管理处， 福建 厦门 361021)

针对基于非线性模型控制器设计困难的问题，将非线性系统用变参数形式的一阶惯性加延迟(FOPDT)模型描述，并进行控制器设计，从而简化控制器的设计过程并提高控制性能.采用一种新型的自适应比例积分(PI)控制器结构，通过增益参数切换和积分复位实现高精度的设定点跟踪和扰动抑制性能.仿真及实验结果表明：文中方法使系统控制精度提高10倍，达到0.01°；超调量有所减少；模型变化时，阶跃响应和干扰抑制效果仍佳；与传统的PI方法比较，文中方法具有良好的动态、稳态响应性能和鲁棒性. 关键词： 变参数一阶惯性加延迟模型； 自适应比例积分； 前项增益切换； 积分复位

近几十年来，对非线性模型控制器的设计方案讨论众多，非常著名的有预测控制[1]、滑模控制[2]、自适应控制[3-5]和LPV控制等[6].近年来,研究者们追求的研究热点之一即为设计过程简单化，它能够解决复杂的非线性问题.因此，本文着眼于众所周知的一阶惯性加延迟型(FOPDT)模型形式，分析讨论特殊形式的变参数FOPDT模型，并设计强鲁棒自适应比例积分(PI)控制器.

1 变参数FOPDT模型

尽管工业被控对象可以很好地用各种非线性数学模型来描述其动态[6-8],但由于模型的非线性表述致使控制器等设计的局限性或复杂性有所增加.传统的工业被控对象通过牺牲非线性特性也可近似用FOPDT描述，该模型进行控制器设计简便易行，但却无法准确地描述被控对象广域的非线性特性.因此,一些研究者已经提出多FOPDT模型描述或控制方案[9-10].文中提出如果FOPDT模型参数依赖于工作点变化而变化，且有规律可循，那么，FOPDT模型可以捕获到整个非线性域的动态特性，其非线性动态模型可以描述为以下的传递函数模型形式，即

(1)

式(1)中：K为稳态增益;tc为时间常数;τ为延迟时间.且K，tc，τ分别为系统某些特征变量w的函数，特征变量表征系统所处工作点.此处,这些函数被表示成多项式形式,即

上式中：wmin≤w≤wmax；am，bn，cl分别表示各多项式系数；m，n，l为各多项式的最高阶次，该类模型称为变参数FOPDT模型.

鉴于控制器设计要同时满足设定点跟踪与扰动抑制性能的问题，基于变参数FOPDT模型,设计了优先考虑扰动抑制性能的自适应PI控制器.基于此设计,自适应PI控制器的前项增益得到满足设定点跟踪性能的控制效果，为同时满足两种控制性能指标,设计前项增益切换机制，进而通过设计较优的积分复位时刻进一步提高系统的动态、稳态控制性能指标.

图1 控制系统结构图Fig.1 Block diagram of control system

2 控制系统

控制系统的结构由自适应调整机制、前向增益切换机制规则、积分复位规则三部分构成，如图1所示.控制器设计有如下4个步骤.

步骤1 设计以扰动抑制性能为主的PI参数自适应控制器，使闭环系统的传递函数与设计的参考模型匹配.

选择设计脉冲响应的参考模型传递函数为

式中：L为脉冲响应的立起时间；α2,α3,…，αn体现了响应的形状；s为复变量.

被控对象式(1)经麦克老林展开变形,可写为

(2)

从扰动到输出的传递函数为

(3)

将式(2)代入式(3),得到与参考模型形式相同的扰动-输出的传递函数模型，并与给定的参考模型匹配，推导出PI的自适应控制器,即

(4)

步骤2 设置前项PI增益，并定义其为{kkp,kki}，以扰动抑制性能为主定义的前项PI增益定义为{kd_kp,kd_ki},此时,该增益不影响步骤1设计的PI参数自适应值，故{kd_kp,kd_ki}均为1；以满足设定点响应性能指标为主的前项PI增益定义为{ks_kp,ks_ki}，设定时在设计的{kd_kp,kd_ki}基准上,减小或增大调整该参数来选取合适的{ks_kp,ks_ki}，使其满足设定点性能指标.

步骤3 设置前项增益参数切换机制，在设定点动态响应过程中完成前项增益参数的平滑切换，具体切换过程为

(5)

式(5)中:kkp∈(ks_kp，kd_kp)或kkp∈(kd_kp，ks_kp)；kki∈(ks_ki,kd_ki)或kki∈(kd_ki,ks_ki)；t0为参数切换开始时刻；t为系统时刻；Δt为参数切换所需时间，其取值在引起可忽略非线性扰动的情况下尽量小，以确保快速的动态响应.

步骤4 设计积分复位(reset)规则，为减小超调，积分复位发生在阶跃响应过程中，在系统响应达到目标值时,进行积分复位，以减少积分项引起的超调量，确保系统响应暂态过程超调更小，稳态精度更高,并进行仿真验证.

3 仿真及实验

图2 温度控制系统实验平台Fig.2 Experimental platform of temperature control system

文中方法在帕尔贴温度控制系统[11]上进行仿真及实验验证.其控制系统除外的帕尔贴设备外观，如图2所示.图2中:通过电流控制铜板温度，其中,铜板和电阻模拟被冷却设备，电阻通电模拟外加干扰.该系统的参数变化FOPDT模型为

其中:τ为常数;K,tc分别表示为

上式中：w为温度控制系统的输入电流.

仿真和实验参考文献[12]，通过设定点跟踪实验验证了积分复位机制的效果.系统初始温度20°时,给定5°的升温阶跃响应，如图3所示.图3中:I为电流；θ为温度；t为时间;PS指增益参数切换;IR指积分复位;实线是自适应PI结合前项增益参数切换和积分复位功能的实验结果;点线是自适应PI结合前项增益参数切换的实验结果.由图3可知：积分复位更进一步加速了动态响应时间，减少了超调.

为验证系统的鲁棒性，除了参考文献[12]的平稳态时外加扰动外，在系统阶跃响应起始时刻外加30W的扰动，并与不加扰动的情况进行比较，结果如图4所示.由图4可知：此时，系统的动态响应指标并未有大的改变，而控制精度却能够达到±0.01°.

图3 PI-PS-IR的设定点跟踪实验 图4 PI-PS-IR的外加干扰鲁棒性实验Fig.3 Set-point tracking experiment Fig.4 Robustness experiment of PI-PS-IR method with external disturbance

另外，改变系统自身模型，将铜板体积增大，系统参数K均减小，tc均增大.仿真时，令变参数K均减小至原有值的80%，或变参数tc均增大至原有值的120%，或二者同时变化，其仿真控制效果，如图5所示.图5中：实线为阶跃响应、500 s时外加干扰和800 s时去除干扰的结果.实验时，将铜板体积增大至原有体积的2倍，做阶跃响应和干扰抑制实验,结果如图6所示.图6(b)中:两条实线分别为升高或降低5°阶跃响应、500 s左右外加干扰和1 000 s左右去除干扰的结果.由图5,6可知：系统模型变化的情况下，所设计的控制系统阶跃响应和干扰抑制效果良好，具有强鲁棒性.

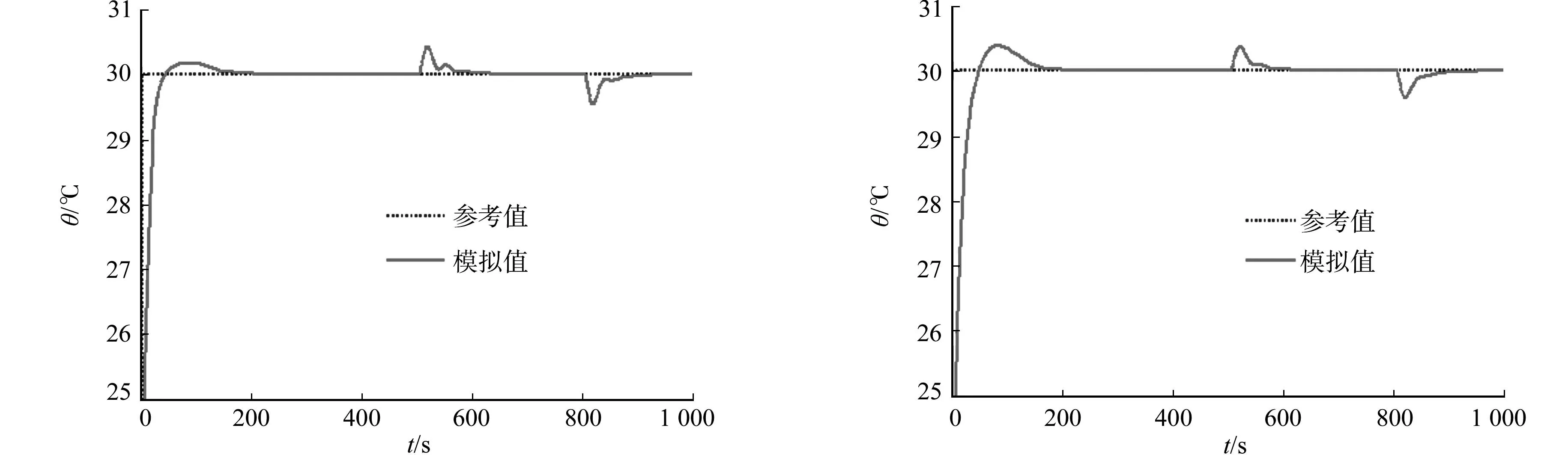
(a) 改变模型参数tc (b) 同时改变模型参数K与tc图5 系统模型变化的鲁棒性仿真验证Fig.5 Robustness simulation verification with system model variations

(a) 铜板体积倍增的实验平台 (b) 实验结果 图6 系统模型变化的鲁棒性实验Fig.6 Robustness experiment for system with model variations

4 结论

1) 针对变参数形式的一阶惯性加延迟型(FOPDT)模型，设计强鲁棒性PI自适应控制器.PI自适应控制器的设计采用麦克劳伦法展开FOPDT模型,并推导出扰动至输出之间的闭环传函，进而与进行参考模型匹配得到自适应律，满足扰动抑制性能，其中,延迟环节不再进行帕德近似，而是直接参与控制器设计.

2) 通过设计前向增益得以满足设定点跟踪性能，在设计前向增益并在前向增益切换的基础上,同时满足设定点跟踪与扰动抑制性能.

3) 通过设计较优的积分复位时刻，能够进一步减少超调.

4) 提出的方法在一个温度控制系统上进行仿真和实验，验证了提出方法.结果表明:该方法控制系统除能够同时满足设定点跟踪与扰动抑制性能外，还具有强鲁棒性.

[1] 胡超芳,解倩倩.非线性系统有输入饱和时基于平方和的鲁棒模型预测控制器[J].控制理论与应用,2016,33(6):321-328.

[2] 杨晓骞,李健,董毅.非线性不确定系统的非奇异快速终端滑模控制[J].控制理论与应用,2016,33(6):772-778.

[3] 谢春利,邵诚,赵丹丹.基于最小二乘支持向量机动态逆的非线性系统自适应控制[J].大连理工大学学报,2012,52(1):100-105.

[4] 张剑丰,刘白雁.电液非线性系统模型跟随自适应控制的离散非线性参考模型方法[J].机床与液压,2005(9):98-100.

[5] 孟珺遐,王渝,王向周.Bang-Bang+Fuzzy-PI自适应控制器的应用研究[J].机床与液压,2008,36(10):266-270.

[6] 殷明,陆宇平,何真.变体飞行器LPV建模与鲁棒增益调度控制[J].南京航空航天大学学报,2013,45(2):202-208.

[7] LIU Xiaoxu,GAO Zhiwei.Takagi-Sugeno fuzzy modelling and robust fault reconstruction for wind turbine systems[C]∥Proceedings of IEEE 14th International Conference on Industrial Informatics.Poitiers:IEEE Press,2016:492-495.

[8] SHAO Hui,NONAMI K,WOJITARA T,etal.Neuro-fuzzy position control of demining tele-operation system based on RNN modeling[J].Robotics and Computer-Integrated Manufacturing,2006,22(1):25-32.

[9] YANG Zhenyu,SUN Zhen,ANDERSEN C.Nonlinear FOPDT model identification for the superheat dynamic in a refrigeration system[C]∥Conference of the IEEE Industrial Electronics Society.Melbourne:IEEE Press,2011:634-639.

[10] BAGHERII P,KHAKI-SEDIGH A.An ANOVA based analytical dynamic matrix controller tuning procedure for FOPDT models[J].Amirkabir International Journal of Science and Research MISC,2010,42(2):55-64.

[11] 邵辉,野波健藏.Peltier热电设备LPV 建模及多参考模型IPD自适应控制[C]∥中国过程控制会议.南京:中国自动化学会,2011:85-90．

[12] 邵辉,胡伟石,罗继亮.基于LPV模型的鲁棒PI控制方法[J].北京工业大学学报,2012,38(12):1761-1765.

(责任编辑： 黄晓楠 英文审校： 吴逢铁)

Strong Robust Adaptive PI Controller Design of Parameter Varying FOPDT System

SHAO Hui1, HU Weishi2, HONG Xuemei1, LUO Jiliang1

(1. College of Information Science and Engineering, Huaqiao University, Xiamen 361021, China;2. Laboratory and Equipment Management Department, Huaqiao University, Xiamen 361021, China)

Since the difficulties exit in designing controller for nonlinear models, the article describes first order plus dead-time (FOPDT) model with parameter varying for nonlinear systems, and proposes to design controller based on it, which simplifies controller designing processes and improves system performance. It is worthy to be mentioned that the article describes a special structure of adaptive proportional integral (PI) control, in which the set-point tracking with high accuracy and disturbance rejection performance are guaranteed by the forward gain switching and integrator reset. The simulation and experimental studies demonstrate that the accuracy of the system is improved to 10 times than before, reaching to 0.01°, that the overshoot is decreased, that the results of step response and disturbance rejection are still well when the system model is changed, and that compared with the traditional PI regulator, the proposed method has good dynamic， steady state performance and robustness. Keywords： first order plus dead-time model with parameter varying; adaptive proportional integral; forward gain switching; integrator reset

10.11830/ISSN.1000-5013.201701018

.tif

2016-09-07

邵辉(1973-)，女，副教授，博士，主要从事机器人控制、运动规划、智能控制、非线性系统建模与控制的研究.E-mail:shaohuihull@163.com.

福建省科技计划项目(2015H0026)； 第48批留学回国人员科研启动基金(Z1534004)

TP 27

A

1000-5013(2017)01-0096-05