双轮车自平衡运动控制系统

郑晋平

(太原理工大学 信息工程学院，山西 太原 030024)

双轮车自平衡运动控制系统

郑晋平

(太原理工大学 信息工程学院，山西 太原 030024)

双轮车的自平衡系统是包括各种特性的复杂系统，鉴于传统控制理论对于系统中出现的不稳定和非线性等问题不能够很好的解决，所以在结合了对象的实际应用和理论特性之后对系统进行了建模和做了详细的分析，并提出模糊控制+比例积分(PI)控制混合而成的控制方法。同时对模糊控制和PI控制分别设计了控制器，根据小车特性完成仿真实验，其阶跃和抗干扰等结果说明模糊+比例积分(PI)控制的方法结构简单、实用、抗干扰程度高，其控制器更是能够很好地达到小车运动平衡控制的目标。

双轮车；模糊控制；运动控制

双轮自平衡车系统包括多个特性，如强耦合，不稳定和非线性等。在整个系统中既要控制保证小车的平衡，又要在此基础上完成其它各个动作，而当下双轮车有关方面都已有所进展：整个系统的控制器会随着其状态的改变而改变，从而使得系统的状态始终是在朝滑模面运动，进一步让系统在受到外界影响及参数变化时增强稳定性，而此方法的不足之处在于系统的轨迹到达滑膜面后会通过滑膜面两侧的往返运动而形成高频抖振[1]，而不会沿滑膜面向平衡点运动；由于LQR是以状态空间给出的线性系统为理论对象，其目标函数则是控制输入的二次型函数，这种控制可以避免高频抖振，虽然降低了整个系统的鲁棒性,但其稳态特性却较为良好；模糊控制有其独特的优点：鲁棒性强，且对控制系统中对象的数学模型精确度要求并不高，这就使得该控制的实用性较强[2]。所以从实际出发既希望整个控制简单化，同时也希望控制的效果更佳，能够减少其他因素的影响，所以提出了一个由模糊控制、比例积分控制(PI控制)共同组成的复合控制系统[3]，并用仿真来说明方案整体的有效性。

1 控制系统的设计

1.1 控制方案的选定

1.1.1 方案的选取理由

首先明确小车的速度和倾角是控制中最重要的两个变量，在实际中所控制的这两者又会相互影响，任意一个变量的改变都会让另一个变量发生变化，两者的耦合性较强，所以在系统设计中也应该根据上述特点将两者进行单独设计。对于小车的控制和运行来说，直立是基础，故运用模糊控制算法来进行控制，选取的控制器为模糊控制器[4]，这样就能够使小车的直立控制器的抗干扰能力及鲁棒性更强。

1.1.2 控制方案设计

对小车的控制和运行进行合理的分析，进一步提出对速度与角度两个变量的控制方案：模糊控制+比例积分(PI)控制。小车控制系统的原理图如图1所示。

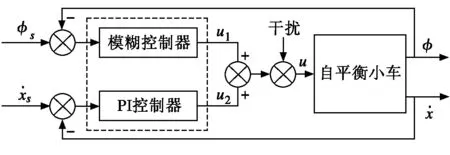
图1 小车模糊-PI控制系统原理图

在图2中，两个控制器分别对小车直立和速度进行控制，直立由模糊控制器负责，速度由PI控制器完成，在两个控制器的同时作用下，小车就会按照给定的速度和角度稳定运行下去。

1.2 控制器的设计

1.2.1 角度模糊控制器的设计

1) 模糊控制参数的确定

在控制系统中模糊控制器[5]的输入量与输出量分别为角度信号与电信号，输入量代表小车运行时与垂直方向的夹角φ及其变化率φc，输出量表示控制器传达给电机的信号u，选定φ、φc和u三者的量化论域是{-6，-5，-4，-3，-2，-1，0,1,2,3,4,5,6}。

2) 模糊控制器的模糊化与隶属函数

输入量、输出量(φ、φc、u)的模糊集为{NB,NM,NS,O,PS,PM,PB}，其隶属度函数同样为三角函数。

3) 建立控制规则

表1所示为控制系统的49条规则，现选择其中一条规则加以注释：Ifφis PB andφcis O, then u is PB。如果小车的倾斜角度是正大、倾斜角速度是零，则小车的倾斜角度不变，若小车的控制器输出为正大，小车便可很快恢复平衡。

表1 控制规则

4) 模糊控制推理及其解

在解模糊中，最常用的是重心、最大隶属度函数和中心平均值三种办法。最大隶属度法将精确值定做在整个论域中对应的最大值，这样可以很简单地进行去模糊的运算，但是精确值所代表的内容比较少。

重心法一般来说也常用于去模糊，将集合中的函数曲线和其轴围成图形的重心对应值作为清晰值。这样能够尽可能用到一切信息，所得值也有较好的鲁棒性，其公式为：

在上述模糊控制器中所涉及的稳定性的分析研究可以通过仿真实验表示。

1.2.2 设计速度的比例积分控制器

积分控制的效果要从多方面考虑，因为其可以做到无差控制，但若是单独使用积分控制就有可能导致结构不稳定，所以一般会在此基础上加入比例控制，形成比例积分(PI)控制器[6]。其传递函数如下：

通过比例积分控制器的传递函数能够知道其极点和零点分别位于坐标原点和负实轴上的z=-Ki/Kp处。

小车的平衡问题与电机的频率响应紧密关联，电机只有能迅速进行正反转的转换和较高的响应频率，才能使小车达到平衡的目标。而且，通过比例积分控制状态和算法输出量的关联可知其波动较大，稳态性能较差，若在实际中用微分计算速度会加剧反馈信号中噪声的影响，所以文中对速度的控制采用比例积分控制。其表达式为：

Δuk=uk-uk-1=Kp(ek-ek+1)+KIek.

2 实验的仿真和分析

本实验在Matlab中将小车经过受力分析后所建立起来的系统模型进行了仿真[6]，并分析系统的阶跃和抗干扰等特性，通过结果验证上述算法的正确性以及获得系统的性能指标。

2.1 系统阶跃响应特性

通过常规比例积分微分控制和模糊控制+比例积分控制两种控制方法来着重对系统速度阶跃响应特性进行研究。

分别选择三个速度值1m/s、1.4m/s、1.7m/s，可得到上述两个控制方法下仿真结果的速度、角度输出曲线图，以1.7m/s为例：

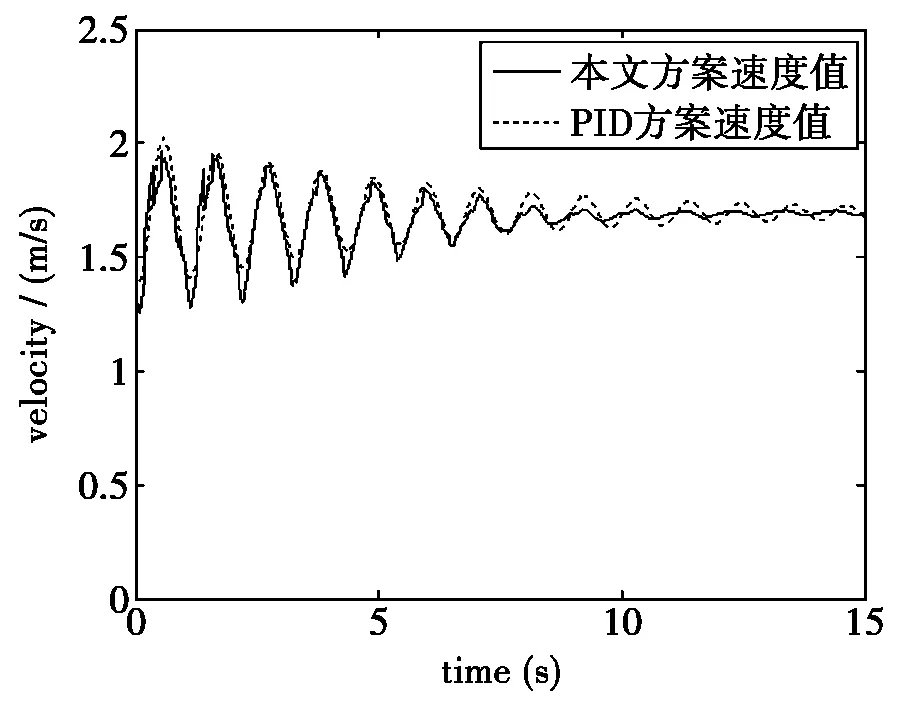
(a) 1.7 m/s的速度输出曲线

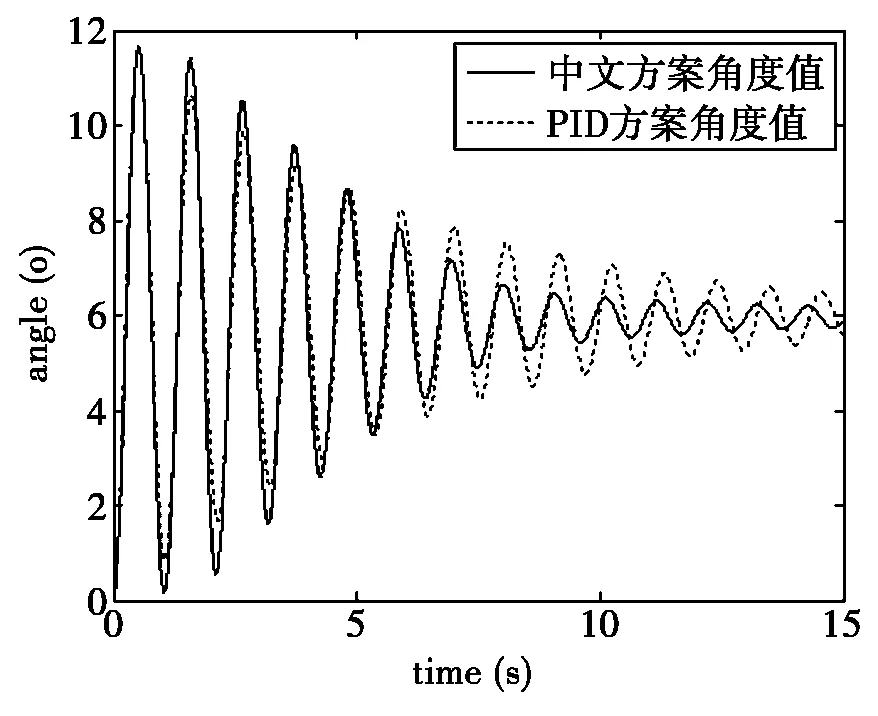
(b) 1.7 m/s的角度输出曲线

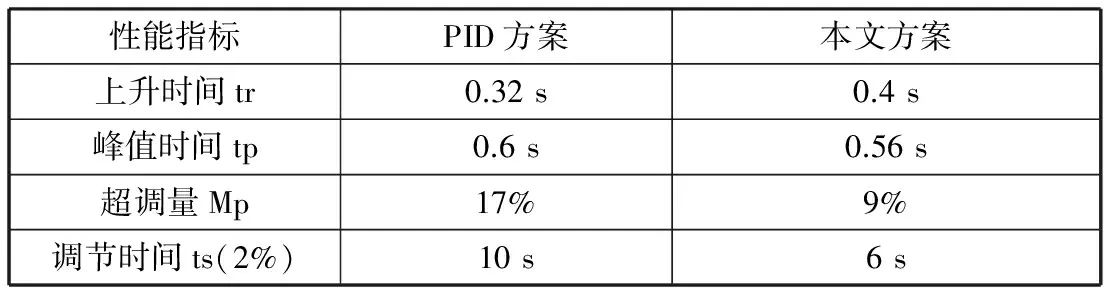
性能指标PID方案本文方案上升时间tr0．32s0．4s峰值时间tp0．6s0．56s超调量Mp17%9%调节时间ts(2%)10s6s

如表2所示可以看到当速度为1 m/s时两种方案的性能指标的比较，经典控制的上升时间虽然短，但超调量大，进而会使得调节时间变大，模糊控制+比例积分控制的超调量小，这样就能够使系统很快进入稳态；通过比较可以发现，本方案在速度为1.4 m/s时控制效果要比经典控制好，而若将速度提升大于1.7 m/s时模糊控制不能满足要求；通过图2可以发现，速度为1.7 m/s时两种控制效果相近，所以在速度接近设定值时震荡幅值小，小车稳定性更好。

2.2 抗干扰特性

由于考虑到小车在实际中会有很多干扰，所以给系统增加了内外部干扰后的仿真，方便对系统抗干扰特性[7]进行分析值，两种控制方案的算法对外部干扰的抗性相差不大。若系统参数发生变化，系统依然能够通过较长的一段时间来逐渐达到稳态，分析上文发现系统的鲁棒性[13]好。

综上，两种控制方案对于外部的干扰的抗性相比本文介绍的方案更佳，系统可以快速完成速度和角度的改变来达到稳态。

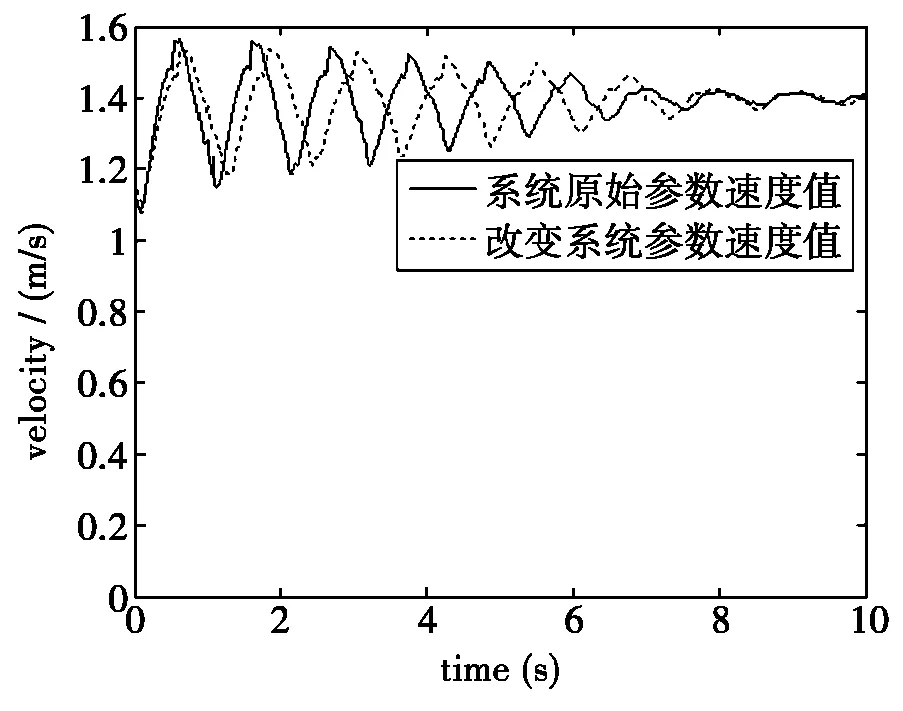
(a) 改变系统参数速度输出曲线

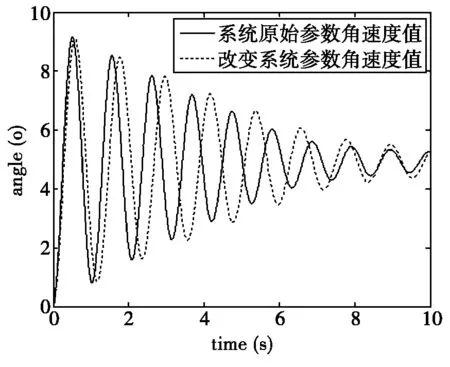
(b) 改变系统参数角度输出曲线

2.3 仿真结果分析

小车的数学模型由于其不稳定性及非线性等因素不能够精准地进行建模，所以要将系统的非线性方程化简成为线性状态方程[8]。而本文中的模糊控制、比例积分控制综合控制正适用于这类实际精准建模困难及经典控制难以奏效的情形。这种角度模糊控制器和比例积分控制器分开设计的综合控制方法能够同时顾及到被控对象的实际应用和其特性，综合控制的方法对数学建模要求低和鲁棒性强的优点以及拥有经典控制动态优品质等方面都有较好的体现，在PID控制中，由于对产生的偏差一直修正可能会引起抖动，但是模糊控制在这方面有所不同，只要不超出一定的范围基本上是不控制的，相对PID控制来说可以在一定的程度上减弱抖动和防止抖动，这样更加符合实际的需求，故其结果带来的效果更好。小车实际运行效果如图4。

图4 小车实际运行曲线

在上图中所显示的小车实际运行的曲线和仿真结果相同，所以小车在这种控制方法下可以匀速且平衡的运行。

3 结论

完整的建立了整个小车系统的模型，同时按照理论和实际的需要提出了模糊控制+比例积分控制的算法，并且将两种控制的控制器进行了设计，达到了系统对小车的平衡的控制，通过仿真可以发现，此方案能够更快地达到稳态，能够更好地抵抗干扰，超调量小，这种控制方法相比经典比例积分微分控制来说能够更好地控制小车的平衡。

[1] 刘金琨，孙富春.滑模变结构控制理论及其算法研究与进展[J].控制理论与应用,2007，24(3)：407-418.

[2] 从爽，张冬军，魏衡华.单级倒立摆三种控制方法的对比研究[J].系统工程与电子技术,2001(11)：49-51，101.

[3] 武俊峰，张继段.两轮自平衡机器人的LQR改进控制[J].哈尔滨理工大学学报，2012(6)：5-9.

[4] 阮晓钢，陈静.基于滑模思想和Elman网络的操作条件反射学习控制方法[J].控制与决策,2011(9)：121-124，129.

[5] Wu J F,Zhang W Y.Design of Fuzzy Logic Controller for Two-wheeled Self-balancing Robot[C].Proceedings of the 6th International Forum on Strategic Technology.Harbin,2011:1266-1270.

[6] Huang Y Z,Chen W D.Design and Implementation of Motion Controller of Two-wheeled Mobile Robot[J].ROBOT,2014，26(1)：40-44.

[7] 王建俊.两轮同轴机器人的自平衡控制研究[J].数字技术与应用,2010(7)：107-108.

[8] 马传翔，杨名利.双轮自平衡机器人的滑模变结构控制研究[J].微计算机信息,2011(1)：70-71，106.

Self Balance Motion Control System Used for Two-wheeled Vehicles

Zheng Jinping

(TaiyuanUniversityofTechnology,TaiyuanShanxi030024,China)

The balance system of two-wheeled vehicles is a complex system with various features. In view of that the traditional control theory cannot solve well the problems of instability and nonlinear in system, so in combination with the practical application and theory characteristic of the object, the paper makes a detailed analysis on the system modelling and made and puts forward a mixed control method with fuzzy control + proportional integral (PI) control. At the same time the controller is designed for both of the fuzzy control and PI control respectively. According to the car features, the simulation experiments is completed, the step and anti-interference results show that the fuzzy + proportional integral (PI) control method structure is simple, practical, high anti-interference, its controller can better achieve a balance control car movement.

two-wheel vehicle; fuzzy control; motion control

2016-11-02

郑晋平(1963- )，女，山西阳泉人，高级实验师，硕士研究生，研究方向：计算机应用及自动控制。

1674- 4578(2016)06- 0026- 03

TP242；TP273

A