基于Matlab/Simulink的杀爆弹蒙特卡洛飞行落点仿真

周家胜，杨 莹，倪庆杰，赵万江，卜祥磊，王红革

(1.海军驻沈阳弹药专业代表室，沈阳110045；2.辽沈工业集团有限公司，沈阳 110045 3.北方华安工业集团有限公司，黑龙江 齐齐哈尔 161000)

基于Matlab/Simulink的杀爆弹蒙特卡洛飞行落点仿真

周家胜1，杨 莹2，倪庆杰2，赵万江2，卜祥磊2，王红革3

(1.海军驻沈阳弹药专业代表室，沈阳110045；2.辽沈工业集团有限公司，沈阳 110045 3.北方华安工业集团有限公司，黑龙江 齐齐哈尔 161000)

弹道仿真软件有助于对杀爆弹的射程进行分析与评定，为此设计了基于Matlab/Simulink环境下的弹道仿真模型，采用速度坐标系给出的弹体质心力学方程，结合杀爆弹在飞行中所受到的干扰因素，列出了在Matlab下应用蒙特卡洛方法仿真随机干扰因素的步骤，实现了弹道仿真。结果验证了仿真方法的有效性。采用Simulink完成弹道建模与仿真，与传统编程语言相比，具有形象直观、易于修改等特点。

干扰；外弹道；蒙特卡洛

杀爆弹的射击密集度是重要战术技术指标，特别对于大口径杀爆弹获得满意的密集度指标是武器系统设计中的重要课题。从以往试验来看，当杀爆弹在试验中出现故障或问题时，试验现场常因欠缺弹道仿真而陷入被动。弹道仿真是研究密集度的重要手段，对杀爆弹采用蒙特卡洛模拟随机干扰弹道的特性，为提高密集度提供依据。近年来，国内关于弹道仿真日益增多，对仿真的需求也日渐丰富。因此，本文以杀爆弹弹道仿真为例，进行系统建模，将造成杀爆弹散布误差的因素带入，对密集度打靶试验进行仿真，最后给出一定条件下的弹道仿真结果来验证仿真的有效性。

1 外弹道数学模型

根据外弹道理论，由弹道切线为一根轴，法线为另一根轴组成的坐标系即为自然坐标系[1]，如图1所示。

图1 自然坐标系

图1为弹丸受力状态，将质心运动矢量方程向自然坐标系二轴分解，根据矢量ax和gx在切线ξ上的投影得到切线ξ上的方程为

所谓自然坐标系的微分方程组即自然坐标轴上分别投影所得到的方程，将上述切向及法向等相关参量联立得坐标系上的质点弹道方程组如下：

积分的初始条件为t=0时

x=y=0

v=v0

θ=θ0

P=Pon

2 蒙特卡洛模拟试验

蒙特卡洛法又称统计试验法，其基本思想是利用计算机的数值模拟来代替飞行试验。其进行弹道仿真步骤如下：一、分析对象的动态特性；二、确定其飞行过程中的随机干扰及分布规律；三、根据干扰及力学模型建模；四、对仿真结果进行处理及分析[2]。影响杀爆弹射击密集度的因素是由火炮、弹药、气象、炮手操作、阵地放列及弹着点测量等方面共同作用的结果，一般体现在弹丸初速、射角、阻力系数等散布。因此，可以通过气象条件、弹道诸元和弹丸静态参数等散布来分析和计算射击密集度。根据靶场试验经验，造成杀爆弹落点散布的随机干扰因素均围绕着指标值上下浮动，因此该程序设定的随机干扰值据指标值以及方差对程序进行设定，产生符合实际情况的随机数带入到程序中，实现带干扰的仿真过程。影响某杀爆弹密集度的误差源见表1。

表1 射击密集度误差源

模型采用炮兵标准气象条件如下[3]：

地面(即海平面)标准气象条件：

气温ton=15℃ 密度，ρon=1.2063kg/m3，

气压Pon=100kPa，地面虚温ζon=288.9K，声速Con=341.1m/s；

空中标准气象条件(30km以下)

对流层(y≤yd=9300，yd为对流层高度)

ζ=ζon-G1y=288.9-0.006328y，

G1=-6.328×10-3。

对于密度函数H(y)，有时采用下列公式

y<9300m：H(y)=(1-2.1904×10-5y)4.4。

3 仿真实现及数据处理

利用Simulink建立微分方程组时主要用积分模块，建立蒙特卡洛模型时主要考虑循环仿真、过零检测及随机变量生成[4]。对于循环模拟打靶试验，可以使用仿真软件中的使能模块，每次循环一个周期使积分归零，重新设定初始值；在过零检测判断条件中，设置弹道高y为判断每次仿真结束标准；针对随机变量产生，则可以设随机变量射角θ，初速v，服从x～N(μ,σ2)，因此在Matlab仿真中利用系统的标准正态分布函数Random Number即可获得一组已知分布的随机变量抽样值。通过弹道仿真，每次获得一组落点坐标作为杀爆弹落点的一个抽样，仿真结束后，可以获得落点散布的标准差，进一步也可计算其密集度[5]，如图2所示。

图2 蒙特卡洛仿真模型

该仿真的结束条件采用杀爆弹的飞行高度来控制，当飞行高度等于零时结束仿真，为防止仿真提前结束，可以将仿真参数的结束时间设置为全弹道的几倍时间。

图3为差值法带入阻力系数模型，方程中阻力系数采用43年阻力定律[6]。

图3 阻力系数模型

4 仿真结果

用Simulink仿真的最大特点就是仿真结果可以根据需求进行绘制，其展现形式有曲线图、散点图、柱形图等。得到的变量数据可以输出到Workspace，方便数据处理与存储[7]。

以某口径杀爆弹为基础，选取一组标准发射条件进行蒙特卡洛打靶试验，采用变积分步长的4阶Ronge-Kutta进行积分运算，获得落点分布情况，图4给出仿真50次的弹道仿真落点分布图。

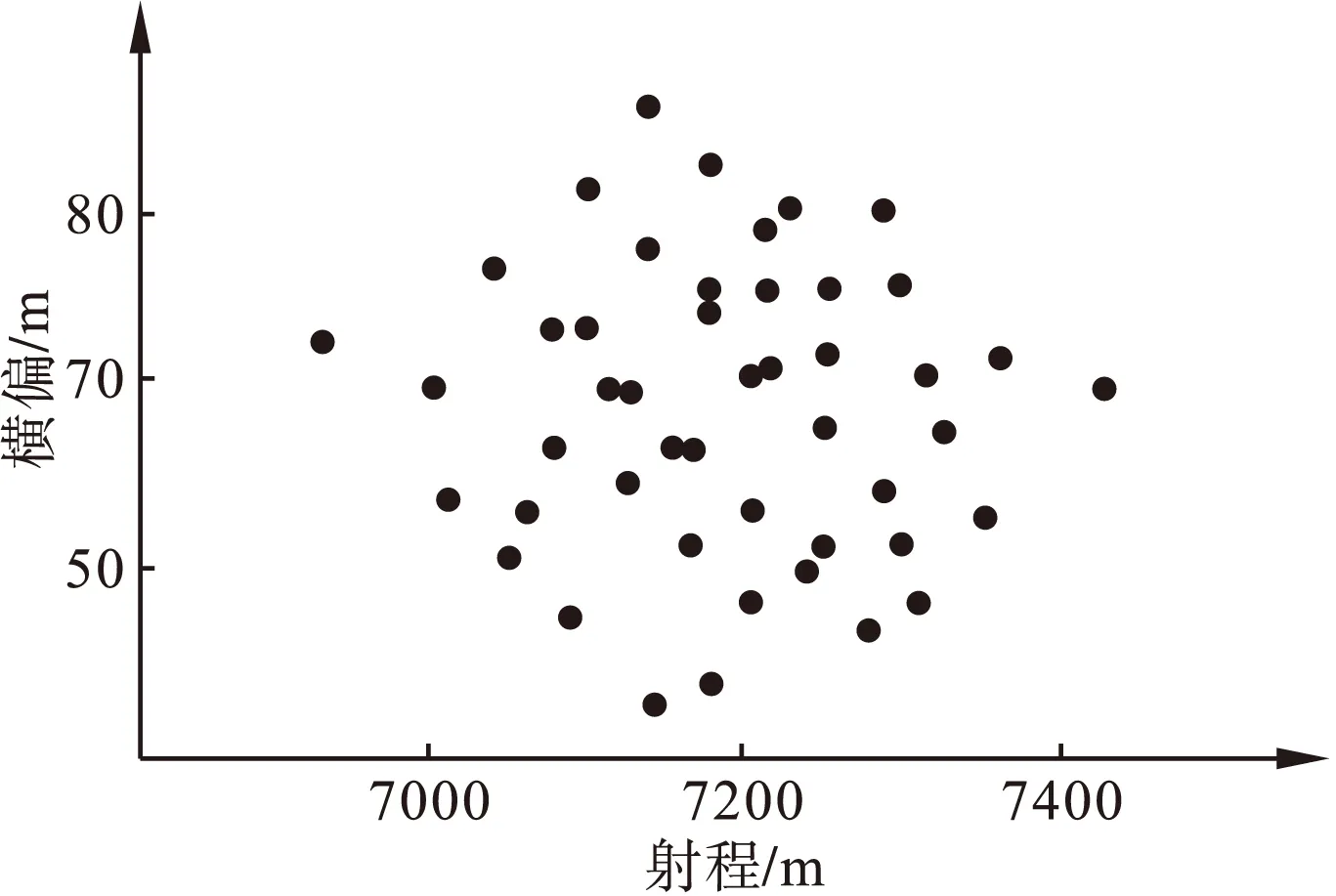
图4 落点分布情况

该型号杀爆弹的落点分布情况与实际打靶试验情况基本一致，验证了该仿真模型的有效性，为今后系统试验奠定了可靠的理论基础。

5 结束语

参考经典弹道方程组，又结合已有的靶试经验，采用Matlab仿真工具建立仿真模型。根据外弹道理论结合蒙特卡洛方法，给出了有干扰情况下，较为准确的获得外弹道诸元的数据，得出杀爆弹射击的落点，为杀爆弹的射击精度研究和验证提供了仿真手段。同时，该系统还具备良好的拓展性，若在该系统加入动力模块，则可用于分析带火箭发动机的弹丸模拟与仿真。

[1]徐明友.高等外弹道学[M].北京：高等教育出版社,2003.

[2]王华，徐军，张芸香.基于Matlab的弹道蒙特卡洛仿真研究[J].弹箭与制导学报,2005,25(S1):181-183.

[3]浦发.外弹道学[M].北京：国防工业出版社，1980.

[4]张志涌.精通MATLAB6.5版[M].北京：北京航空航天大学出版社,2003.

[5]赵军民，何亚娟.基于Matlab/Simulink的弹道仿真模块化设计[J].弹箭与制导学报,2007,27(1):147-153.

[6]王中原，周卫平.外弹道设计理论与方法[M].北京：科学出版社,2004.

[7]李颖.Simulink动态系统建模与仿真基础[M].西安：西安电子科技大学出版社,2004.

(责任编辑：马金发)

Simulate Research of the High Explosive Bomb Flight Landing with Monte-Carlo Method Based on Matlab/Simulink
ZHOU Jiasheng1，YANG Ying2，NI Qingjie2,

ZHAO Wanjiang2,BU Xianglei2，WANG Hongge3

(1.Military Representative Office of Nary Ammunition in Shenyang Area,Shenyang 110045,China;2.Liaoshen Industries Group Co.,Ltd,Shenyang 110045,China;3.Beifang Huaan Industries Croup Co.,Ltd,Qiqihaer 161000,China)

The simulation software is helpful to the analysis and evaluation of high explosive bomb range,so the simulation model is designed based on the Matlab/Simulink environment,using the barycenter mechanical equations of velocity coordinate system and combining the interference factors in flight,and the steps in the application of Monte Carlo method in the simulation of random interference factors are shown,realizing trajectory simulation.The results verify the validity of the simulation method.The motion of the projectile can be simulated,and the reliability of the simulation is verified with theoretical calculation.

interference;exterior ballistic;Monte-Carlo

2016-05-29

周家胜(1968—)，男，高级工程师，研究方向：弹药工程。

1003-1251(2016)06-0099-03

TJ413.4

A