能量双向流动的蓄电池充放电系统设计

史永胜， 高婧茹， 刘言新

(陕西科技大学 电气与信息工程学院， 陕西 西安 710021)

能量双向流动的蓄电池充放电系统设计

史永胜， 高婧茹， 刘言新

(陕西科技大学 电气与信息工程学院， 陕西 西安 710021)

针对现有蓄电池充放电装置存在的交流侧电流波形畸变严重、功率因数低等问题，设计了一种能量可以双向流动的充放电装置，前级采用三相PWM整流器，后级采用Buck-Boost双向DC/DC变换器，根据蓄电池充放电方式研究了前后两级的联合控制策略，实现蓄电池的恒压或恒流充电以及放电控制,并利用PLECS软件进行仿真.仿真结果表明：该系统具有较高功率因数及低谐波畸变率.

充放电； 能量双向流动； PWM整流器； Buck-Boost变换器

0 引言

随着能源短缺和环境污染问题的出现，蓄电池开始被大量应用于储能电站、电动汽车以及新能源领域，目前国内使用最广泛的大功率蓄电池充放电技术是通过晶闸管的相控整流来实现的[1-3]，这种

装置交流侧电流波形畸变严重，功率因数低，严重污染电网；且自动化程度低，操作复杂，易出现故障，可靠性不高.

本文针对现有充放电装置存在的问题，研究了能量可以双向流动的一种充放电装置，既可以实现对蓄电池进行充电，也可以实现对蓄电池放电.其

前级采用了三相PWM整流器，可以将交流电转换为直流，也可将直流电逆变回馈到电网，并且都能保证电流畸变率小，减小对电网中引入的无功电流.后级采用Buck-Boost变换器，可将PWM整流器的高电压进行降压和蓄电池匹配[4-9]，也可以将蓄电池电压升高再通过PWM整流器将能量回馈到电网.

1 充放电系统结构

当充电时，PWM整流器工作于整流状态，通过控制功率管VT1，并保持VT2始终断开，这时Buck-Boost电路实质上就是一个Buck电路，将PWM整流器的电压降压之后给蓄电池充电.当需要放电时，PWM整流器工作于逆变状态，控制功率管VT2，同时保持VT1始终关断，这时Buck-Boost电路实质上就是一个Boost电路，通过它将蓄电池的电压升高到电网电压峰值以上，再控制

PWM整流器将蓄电池的电能回馈到电网中，其结构如图1所示.

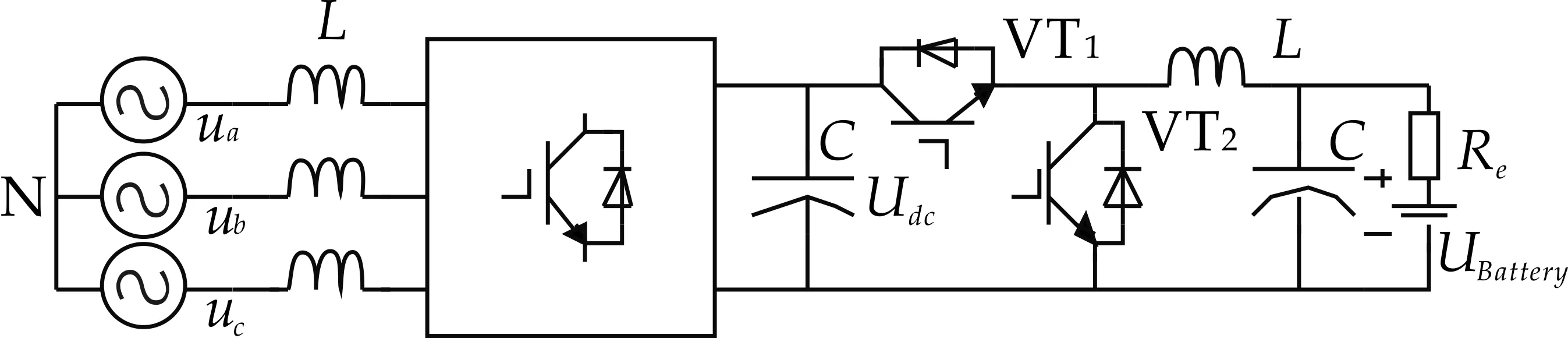
图1 充放电结构图

2 核心算法设计

本文需要控制PWM整流器和Buck-Boost变换器实现对蓄电池的充放电.因为本系统前后两级相互独立，因此两者可以分开控制.

2.1 三相PWM整流器控制策略

三相电压源型PWM整流器一般采用双闭环控制结构的设计方案，内控制环为电流闭环控制，外控制环为电压闭环控制[10-15].本文交流侧电流内环采用基于电流前馈解耦的旋转坐标下的PI控制，直流侧电压外环采用PI控制，系统控制框图如图2所示.

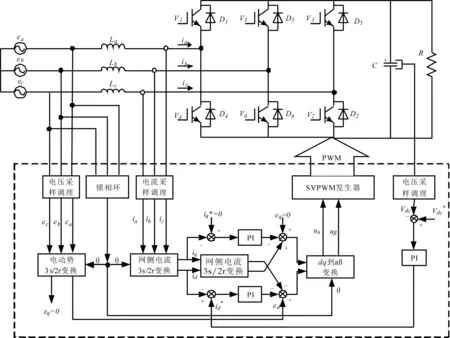
图2 PWM整流器前馈解耦控制框图

2.1.1 电流内环设计

针对电流内环设计而言，得到电流解耦之后的系统内环传递函数框图，如图3所示.

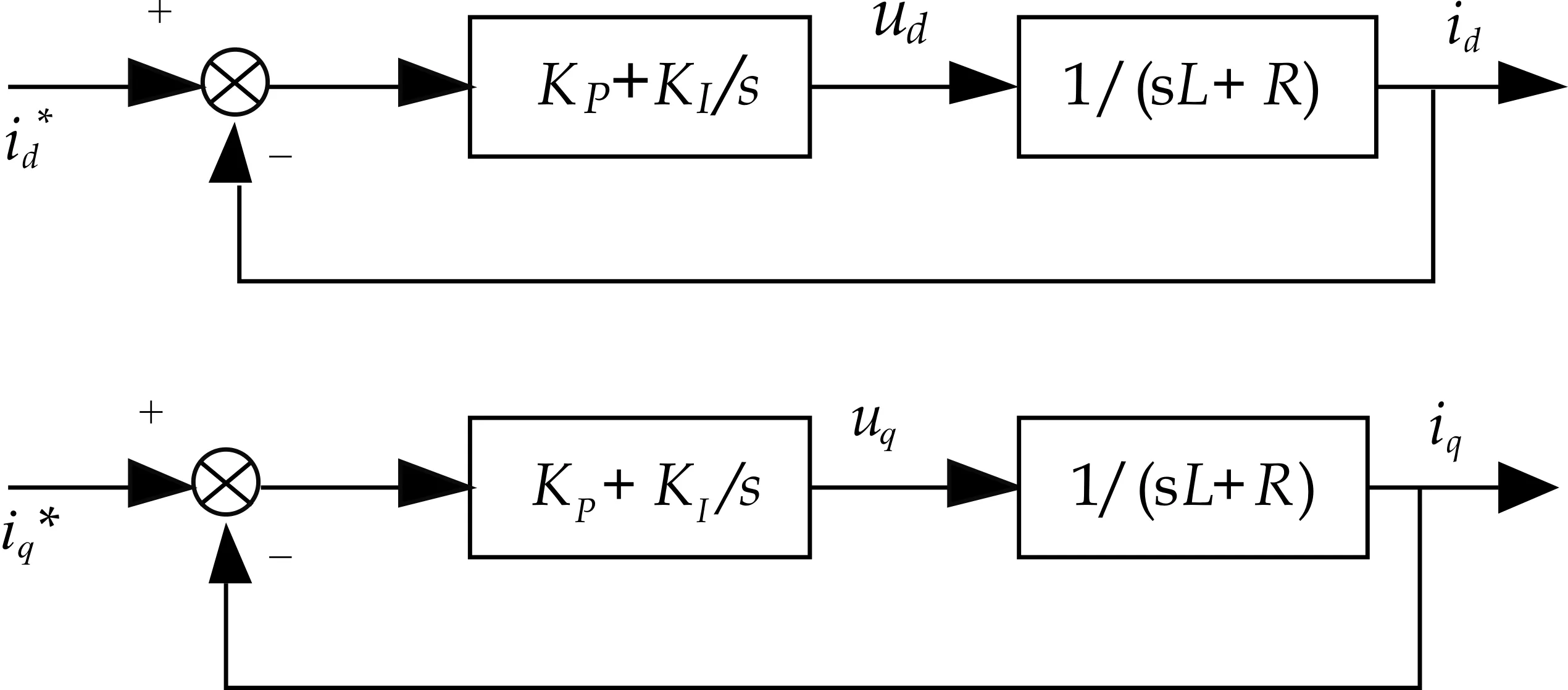
图3 电流内环控制框图

图(3)中KP以及KI分别代表电流比例积分调节器的比例以及积分系数，1/(sL+R)代表控制模型的输入输出关系.以id电流环做为例子，系统闭环输入输出关系为：

(1)

选择合适的KP以及KI系数，令KI/KP=R/L，即可将式(1)简化成一阶惯性环节，如式(2).

(2)

根据典型一阶惯性单元特性可知，其调节时间ts=3Tc，令ts=0.002 s，则Tc=0.000 67，可得KP以及KI跟Tc的关系如式(3).

(3)

式(3)中等效电阻R的表达式为：

(4)

式(4)中：Udc表示PWM整流器直流侧电压，ea表示电网a相电压，ia表示PWM整流器交流侧a相电流.代入数值后，可得R=26.455 Ω.将电感及等效电阻值代入式(3)就可以求得电流内环控制器参数为KP=4.48，KI=39 485.08.

2.1.2 电压外环设计

如果设Vdc*为电压外环的期望值，Vdc为电压外环的反馈值，ic为电容电流值，可得电压外环控制的输入输出关系框图，如图4所示.

图4 电压外环控制框图

设比例控制系数为KP，积分参数为KI，那么可以求得系统闭环传递函数为：

(5)

令

(6)

令闭环传递函数降阶，变为典型二阶系统，可以得到

(7)

一般选取ξ=0.707，电流内环调节时间ts=0.002 s，电压外环需要给电流内环留出足够的调节时间去跟踪给定电流，因此令电压外环调节时间ts=0.1 s，典型二阶系统调节时间为：

(8)

通过计算可以得到ωn=49.5.

因此，可以得出：KP=0.036 8，KI=0.12.

2.2 Buck-Boost变换器控制器设计

Buck-Boost变换器给定量以及输出电压或电流都是直流量，可以采用通常所使用的PID控制，就可以获得良好的静态以及动态响应，因此这里不再讨论别的控制算法，而是直接选用PID控制作为变换器的控制算法.下面就计算具体的控制器参数.

2.2.1 Buck部分恒压控制

根据第三章中推导得到的传递函数并将其变形为：

(9)

可以看出这是一个二阶系统，写出PID的传递函数为：

(10)

将其改写成式(11)的形式：

(11)

为了降低系统阶次，可以令TcKD=LC/Vg，TcKP=L/(RVg)，TcKI=1/Vg，从而可以得到，KP=L/(TcRVg)，KI=1/(TcVg)，KD=LC/(TcVg).

这时，可以求出系统的开环传递函数为：

(12)

不难发现，利用PID的零极点对消将系统校正成了一个积分单元，那么它的闭环传递函数就将是一个一阶惯性环节，消除了Buck变换器的谐振峰值，使系统更加稳定，而且不会出现超调，也就不会对蓄电池产生过电压充电，有利于保护蓄电池安全，不会对其寿命造成影响，闭环传递函数为：

(13)

同样Tc决定了Buck变换器的响应速度，由于只含有一个参数，并且也知道参数对系统的影响变化规律，因此就可以很容易地根据仿真与实验找到合适的Tc值，令ωcTc=1，ωc代表Buck电路截止频率，本文取ωc=20 rad/s.并将本文装置的实际参数代入，可以求得PID参数KP=0.116、KI=0.278、KD=0.019.2.2.2 Boost部分恒压控制

前面求得Boost变换器输出对占空比的传递函数如公式(14).

(14)

式(14)中：代表Boost输出端等效电阻，令式(11)中TcKD=LC/D′2，TcKP=L/(RD′2)，TcKI=1，从而可以得到，KP=L/(TcRD′2).因此可以求得系统的开环传递函数如式(15).

(15)

容易求得系统的闭环传递函数为：

(16)

要使得系统稳定，就必须令闭环传递函数的所有极点在复平面的左半平面，即要满足：

(17)

因为D′2、R、L、UI均大于零，所以可以求得：

(18)

只要Tc满足上式则系统就是稳定的，将系统参数代入可计算得到Tc>0.231，本文取Tc=1，可以计算得出KP=0.415，KI=1，KD=0.007.

3 仿真分析

3.1 PWM整流器整流状态仿真

图5为利用PLECS搭建的三相PWM整流器模型，图6是PWM整流器运行于整流状态，直流侧带电阻负载测试的波形和数据.对蓄电池充电时，需要控制PWM整流器直流侧电压能稳定在某一个恒定值上.在0.2 s之前将直流侧电压给定为150 V，图7中Udc就是实际的直流侧电压，可以看到在0.2 s之前直流侧电压波形一直稳定在150 V基本没有误差，稳态性能达到了期望的需求.在0.2 s时，给定电压突变为200 V，实际的直流侧电压会跟随给定电压上升，最后经过大约0.08 s就基本达到了200 V，其动态响应较快，电压纹波约4 V.

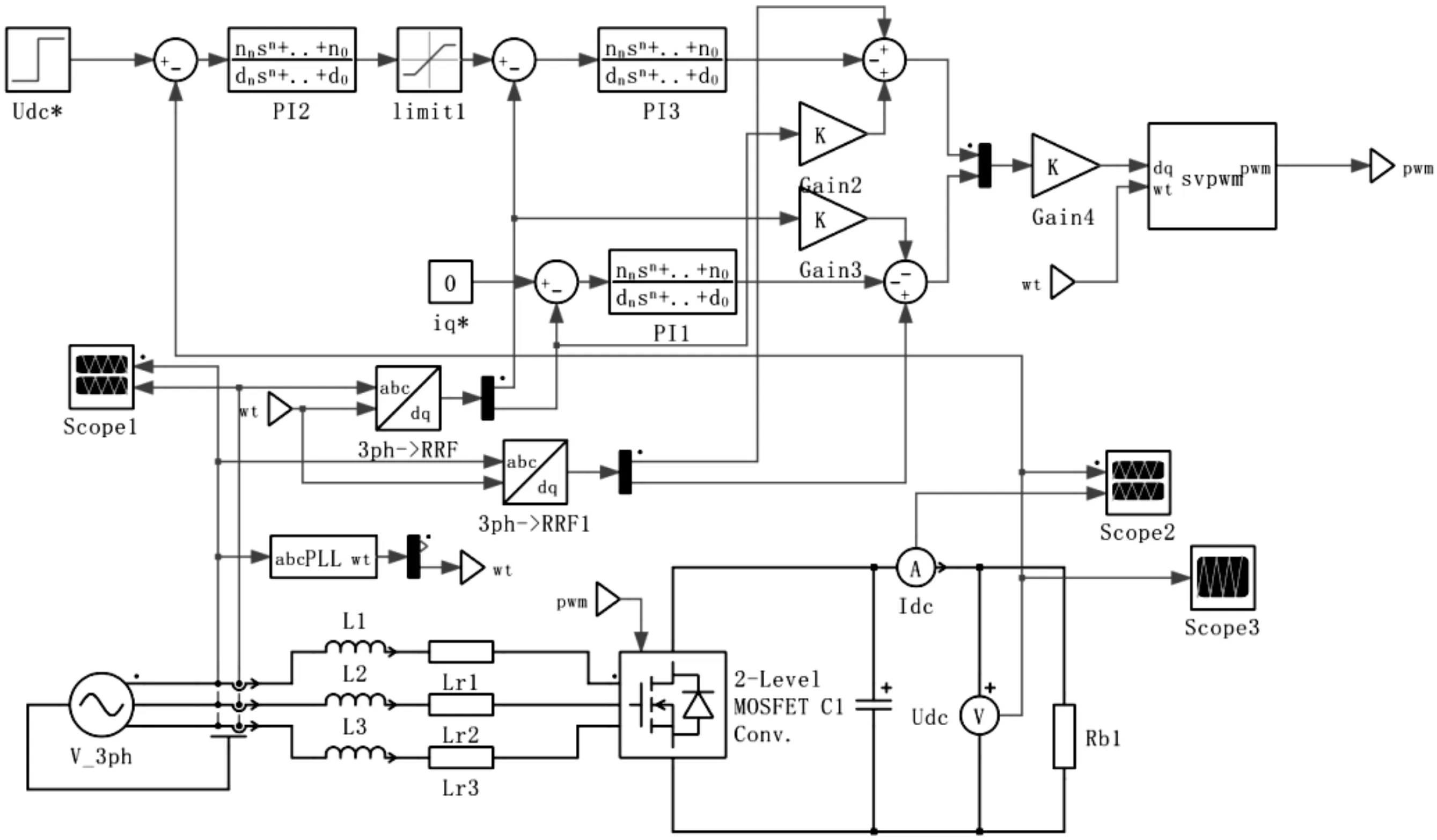
图5 PWM整流器模型

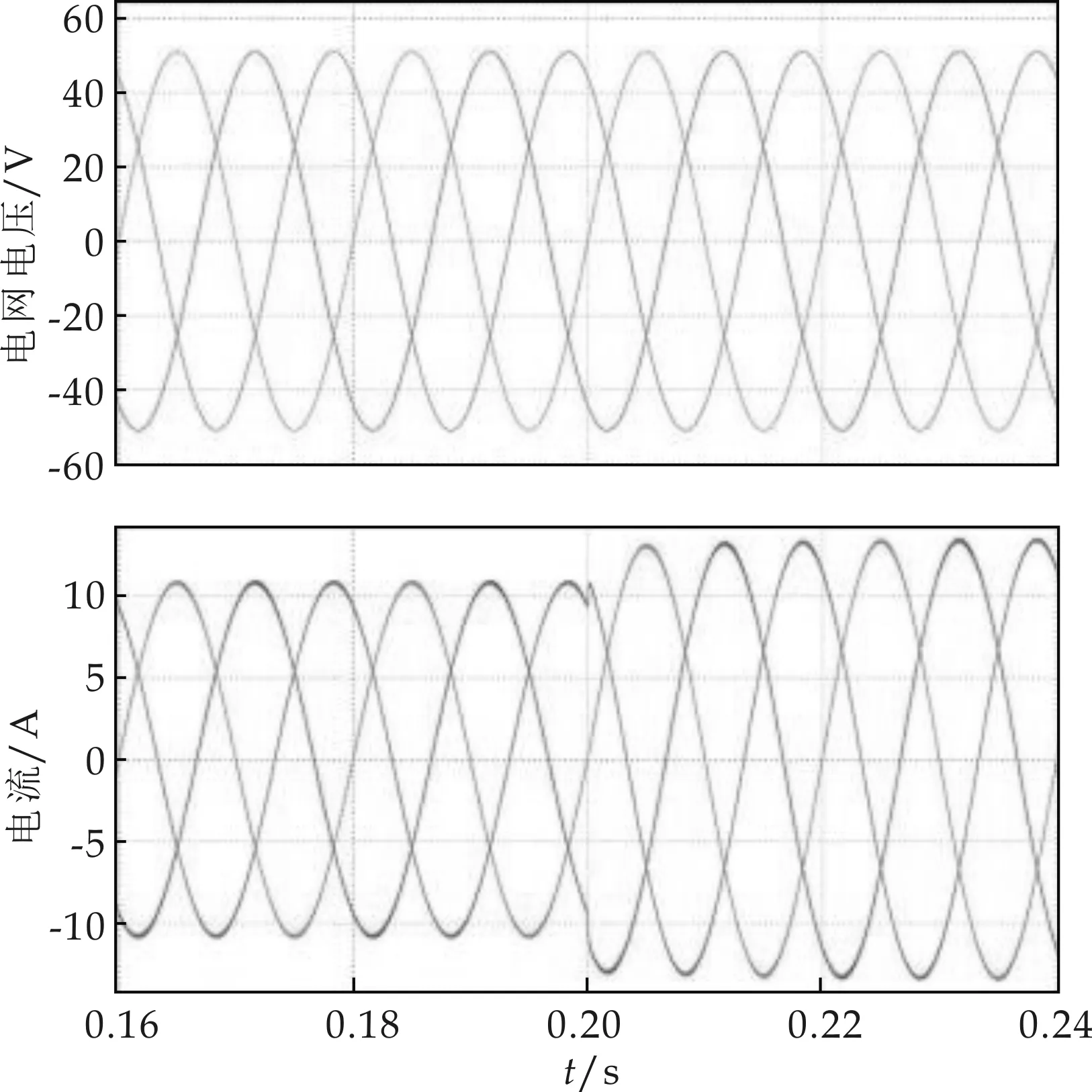
(a)整流状态三相电流波形

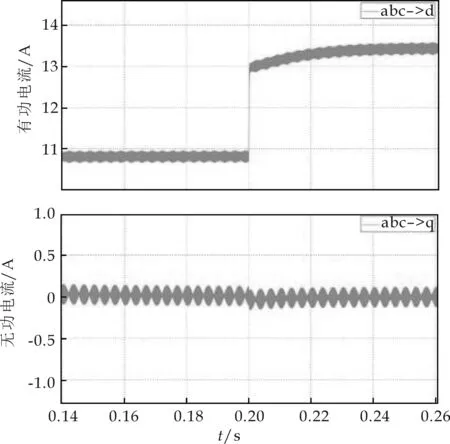
(b)整流状态dq坐标系下电流波形图6 整流状态PWM整流器电流波形

图6(a)是PWM整流器运行于整流状态时的电流波形.图中上半部分是电网电压波形，下半部分是其交流侧电流波形，可以看出电网电压是标准的三相正弦电压波形.0.2 s之前能看出其的交流侧电流波形也是较为标准的正弦波，没有明显的畸变，而且其电流与电网电压是同频同相的，即实现了交流侧单位功率因数的目的.电流波形在0.2 s发生了变化，abc三相电流都在瞬间变大了，这是因为在0.2 s时将直流侧电压给定增大到了200 V，而直流侧电阻没变，对应的直流侧消耗的功率增大了，所以交流侧电流也会增大，这就是我们这里看到的电流波形变大的原因.图6(b)是PWM整流器有功和无功电流波形，其中上半部分是有功电流，下半部分是无功电流.从图中看以发现有功电流在0.2 s之前是大约10.9 A，在0.2 s之后变为大约13.4 A，而在整个过程中无功电流一直保持在0附近，其误差峰值大约为0.2 A，从这个图中就能清晰准确的看出前级使用PWM整流器后，不会对电网造成无功电流污染.

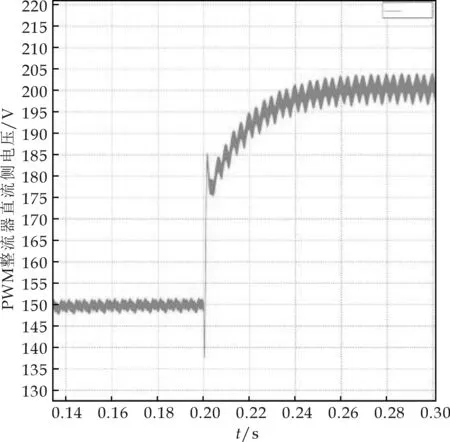
图7 直流侧电压波形

3.2 PWM整流器逆变状态仿真

图8为PWM整流器逆变状态模型.首先令PWM整流器交流侧电流为5 A，在0.2 s的时候再将其改为8 A，就能看出其稳态和动态性能.

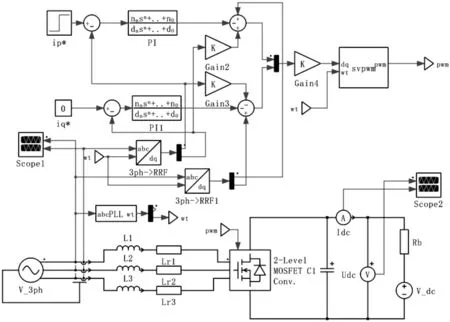
图8 PWM整流器逆变状态模型

图9(a)上半部分是电网电压，下半部分是电网电流波形，从图中可以看到系统的电流是与电网电压同频反相的，前面可以看到在整流状态时，电流是与电网电压同频同相的，但在逆变时是反相的，这和交流侧电流的正方向定义有关.本文中定义PWM整流器交流侧电流输入为正，那么当电流与电网电压同相时其功率就为正，代表了此时功率是从电网流向PWM整流器，而当电流与电网电压反相则代表功率为负，此时功率是从PWM整流器流向电网的.因此图9(a)中所示的电流波形就代表了此时电能是从PWM整流器的直流侧流向电网的，即将蓄电池的电能回馈到了电网.在0.2 s时，将网侧电流幅值突然由5 A变到了8 A，可以看到PWM整流器可以瞬间响应电流变化，变为8 A的交流电流.

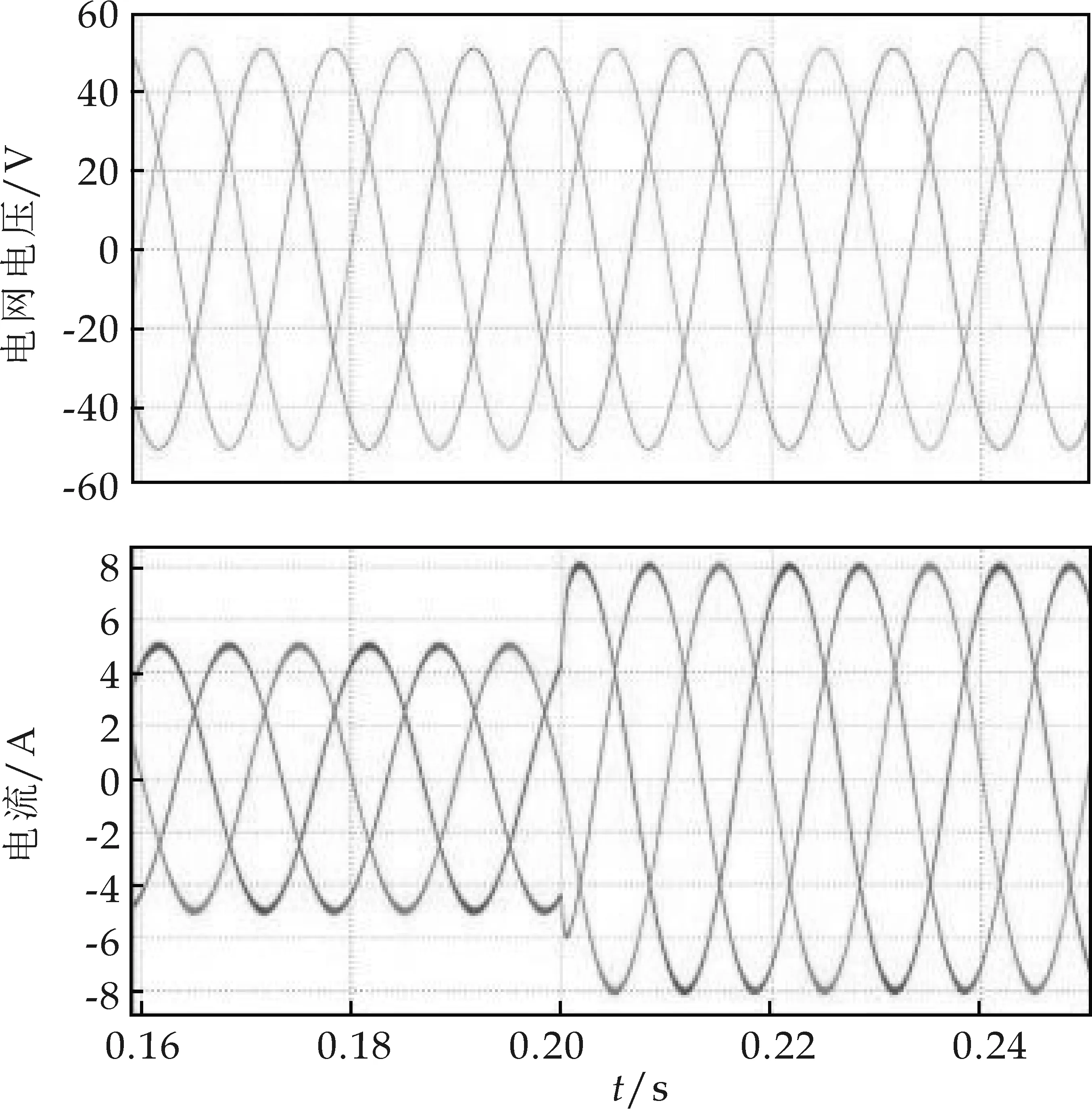
(a)逆变状态三相电流波形

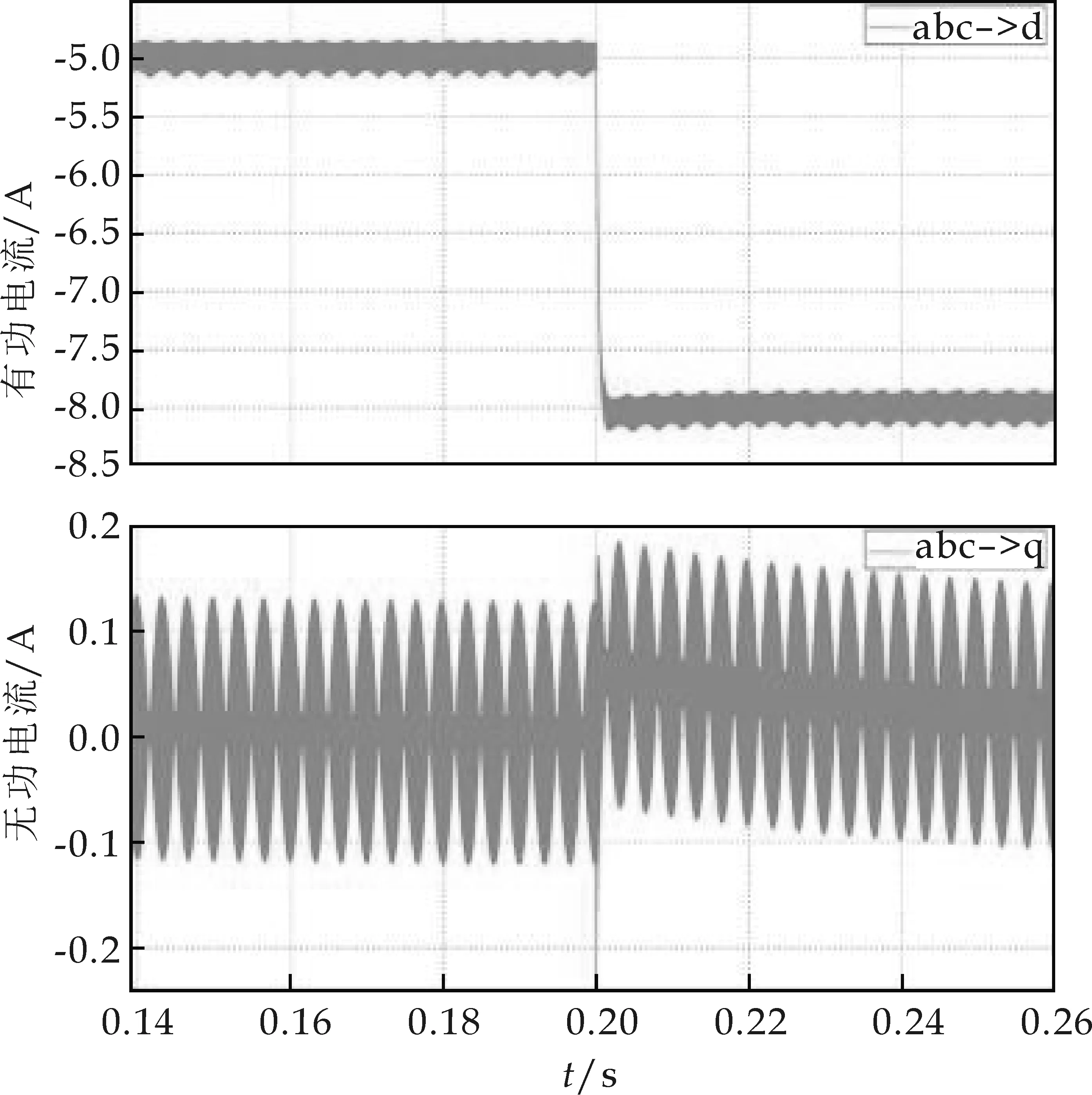
(b)逆变状态dq坐标系下电流波形图9 逆变状态电流波形

图9(b)是系统dq坐标系下的实际电流，在电网电压定向时，令d轴和电网电压综合电压矢量重合，因此d轴上的电流就是系统的有功电流，q轴电流是系统的无功电流，实现将蓄电池电能以单位功率因数的电流回馈到电网，即系统无功电流为0.从图中也可以看出无功电流始终保持在0附近，有功电流则在0.2 s时从-5 A变为-8 A.

0.23 s前 PWM整流器的交流侧电流各次的谐波电流和电压相对于基波而言基于为零，电流谐波中5以及7次谐波的含量是最大的，占到了基波的约0.5%，其余各次谐波则是更小.由此可见PWM整流器运行于逆变状态同样也可以使其交流侧电流波形正弦化，畸变率完全满足要求.0.23 s之后的电流谐波分析结果，而这时的5次谐波占了基波电流的越0.3%.可见当系统电流变大了之后，电流畸变率还反而在减小，因为当电流变大后，控制误差就会相对的减小.

通过上面的分析发现，无论是模拟对蓄电池充电还是对蓄电池放电，前级的 PWM整流器都能满足之前预期的要求，这即证明了系统方案选择的正确性，也证明了前面控制其设计的合理性.

3.3 Buck变换器恒压控制仿真

图10为Buck恒压控制模式的系统模型.图11(a)是恒压Buck模式的仿真结果，在0.1 s之前给定直流电压为80 V，0.1 s之后变为86.8 V，从仿真结果能够看出，系统能够准确地跟踪参考电压，并且当电压变化时，可以在约0.01 s达到新的稳态值.图11(b)为电压电流放大图，在86.8 V时电压纹波约1.1 V.

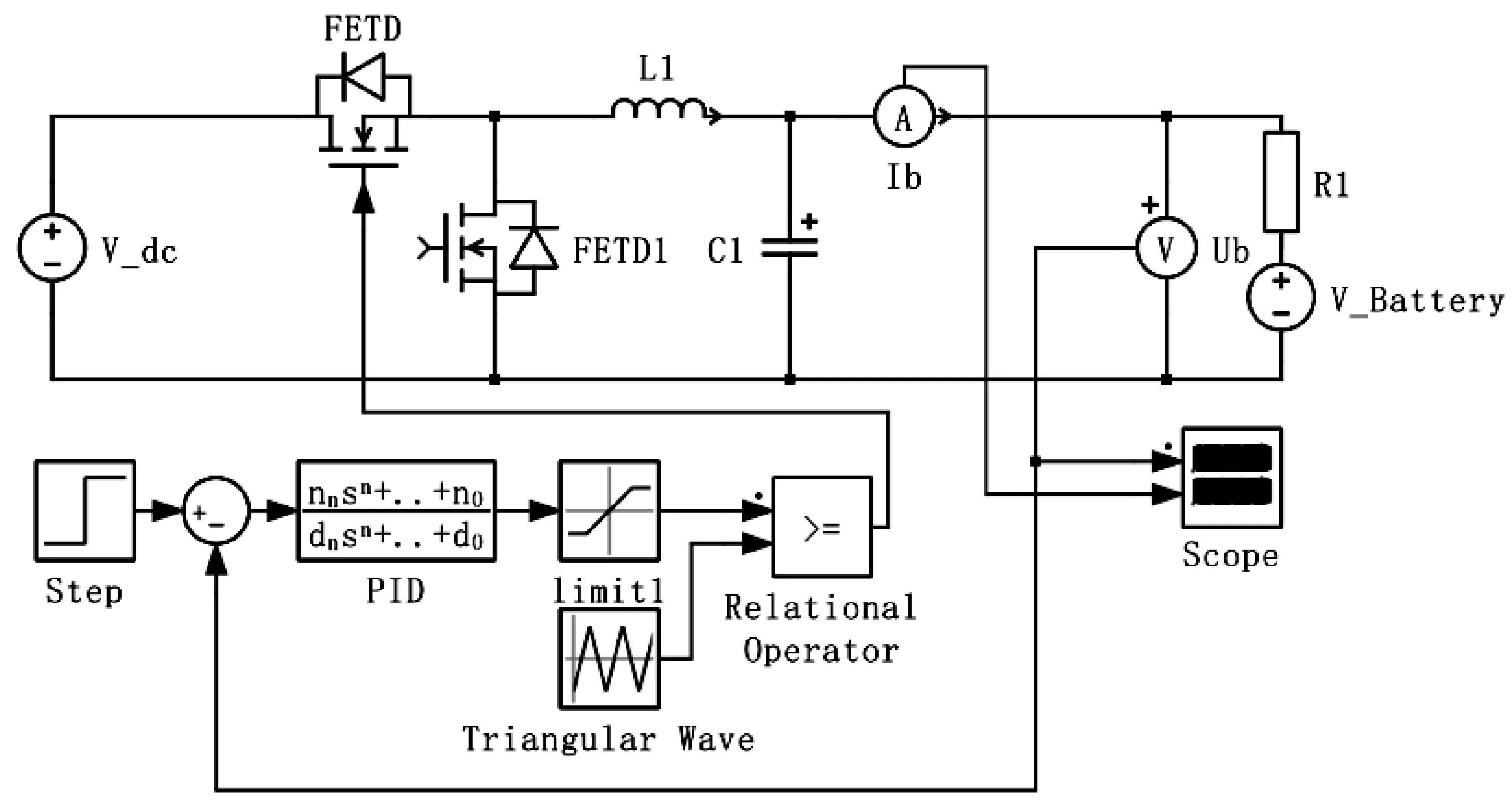
图10 恒压控制模式

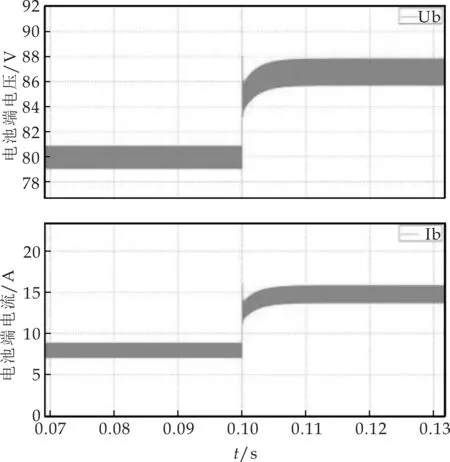
(a)充电电压电流波形

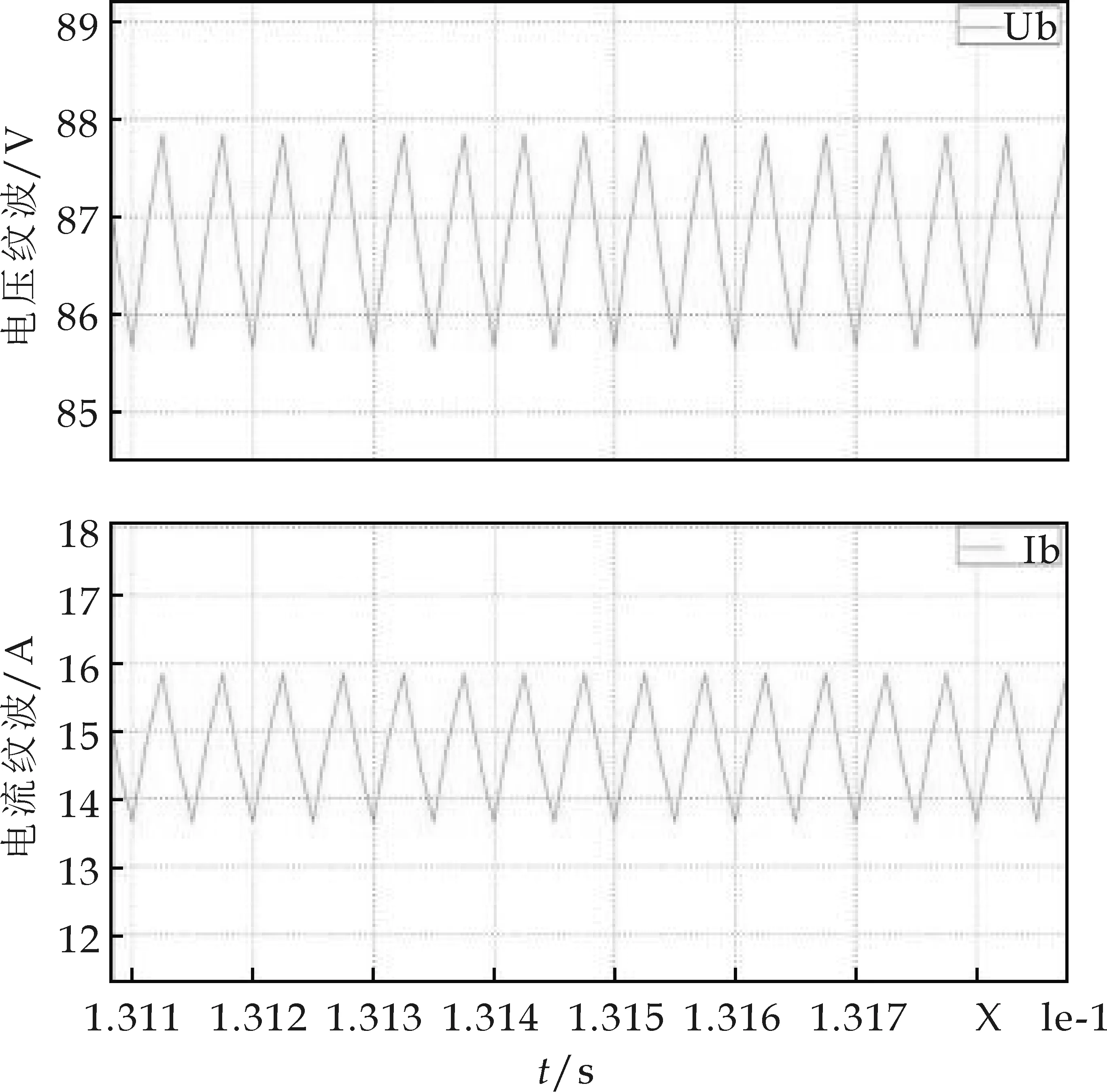
(b)电压电流放大图图11 充电电压电流波形

3.4 Buck变换器恒流控制仿真

图12为恒流充电模型.图13(a)是恒流控制时的结果，0.1 s之前电感电流可以稳定在8 A，0.1 s之后将给定电流改变为10 A，从图中可以看出电流几乎在小于0.005 s的时间内就能够跟踪给定并稳定在10 A.图13(b)为电压电流放大图，电流纹波约0.25 A.

图12 恒流充电模型

(a)充电电压电流波形

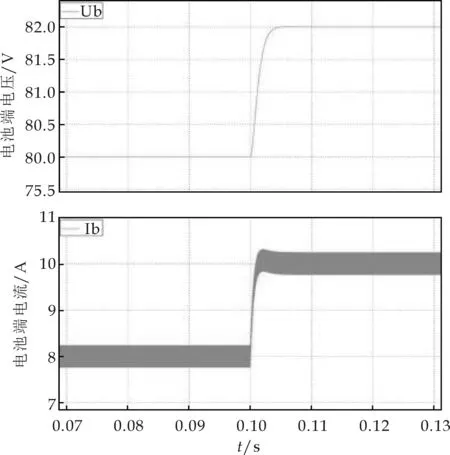
(b)电压电流放大图图13 充电电压电流波形

4 Boost变换器仿真

图14为Buck-Boost变换器处于Boost模式的系统模型，即放电模型.图15(a)为仿真结果，在1s之前将电压设置为150 V，Boost电路可以将输出电压稳定在150 V，在1 s的时候将电压给定突然改变为200 V，Boost变换器经过调节之后也会输出到200 V，在调解过程没有超调，调节时间约为0.1 s.另外将200 V时电压放大，如图15(b)所示，可以看出其电压纹波为6.5 V.

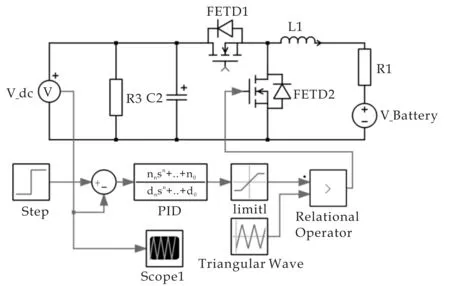
图14 放电模型

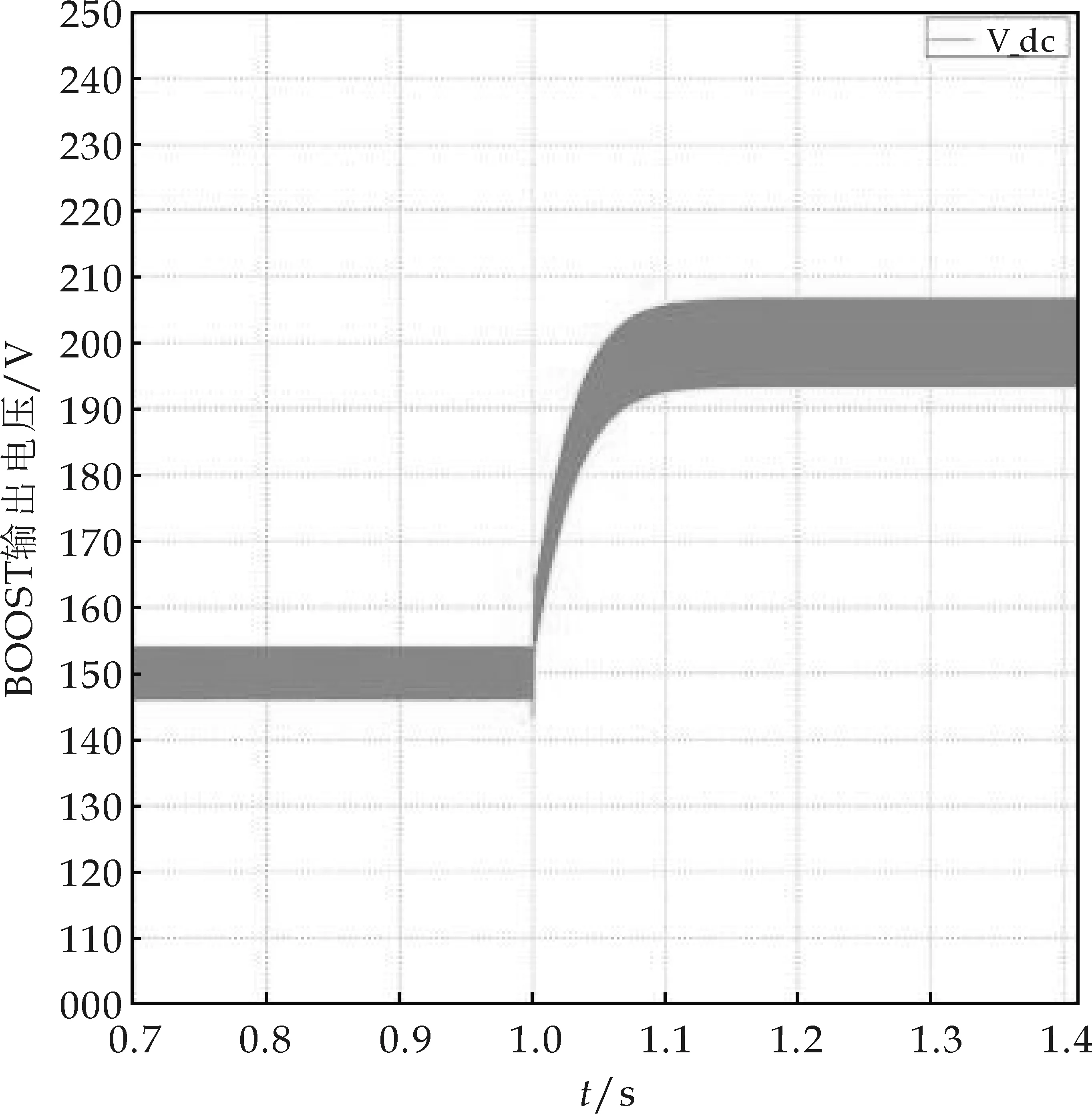
(a)Boost输出电压波形

(b)电压局部放大图图15 输出电压波形

5 结论

通过仿真分析可知，本装置可以实现对蓄电池的充放电控制，且系统具有较高功率因数及低谐波畸变率.验证了方案和控制器的正确性，也验证了本系统的可行性.

[1] 李武峰，罗小英，边孝成,等．电动汽车蓄电池充放电装置研究[J].电力电子技术，2013，47(8)：89-91．

[2] 熊佩鑫，李正明，焦道海．基于ARM&DSP的分布式蓄电池储能系统设计[J].电测与仪表，2014，51(5)：83-86．

[3] 杨孝志．一种节能型蓄电池充放电装置的研究[J].电气传动自动化,2008,30(1):8-10.

[4] 彭思敏．大型蓄电池储能系统接入微电网方式及控制策略[J].电力系统自动化，2011，35(16):38-43．

[5] 冯 韬.高功率因数锂离子电池充放电系统的研制[D].北京：北京交通大学,2008.

[6] Suhara E M,Nandakumar M.Analysis of hysteresis current control techniques for three phase PWM rectifiers[C]//IEEE International Conference on Signal Processing,Informatics,Communication and Energy Systems.Kozhikode:IEEE Kerala Section and National Institute of Technology Calicut (NITC)，2015：1-5.

[7] 张伟华．基于PWM整流器的机车蓄电池充放电装置研究[J].电力电子技术，2009，43(9)：76-78．

[8] 朱永亮，马 惠，张宗濂．三相高功率因数PWM整流器双闭环控制系统设计[J].电力自动化设备，2006，26(11)：87-91．

[9] Singh B，Singh B N，Chandra A，et al．A review of three-phase improved power quality AC-DC converters[J].IEEE Transaction on Industrial Electronics，2004，51(3)：641-660．

[10] 董丽凤，李艳丽．三相电压型PWM整流器的滑模变结构无源控制[J].电测与仪表，2014，51(5)：46-50．

[11] 郑忠玖.三相电压型PWM整流器控制策略及应用研究[D].大连：大连理工大学,2011.

[12] 任晓鹏.三相光伏并网逆变器关键技术的研究[D].北京：华北电力大学,2014.

[13] Georgios Tsengenes． A three-level space vector modulated grid connected inverter with control scheme based on instantaneous power theory[J].Simulation Modelling Practice and Theory，2012，25:134-147.

[14] 张方华，朱成花．双向DC-DC 变换器的控制模型[J].中国电机工程学报，2005，25(11):46-49．

[15] 黄 罡.三相高功率因数PWM整流器及其控制策略研究[D].长沙：湖南大学,2007.

【责任编辑：蒋亚儒】

Design of charging and discharging system with bidirectional energy flow for battery

SHI Yong-sheng， GAO Jing-ru， LIU Yan-xin

(College of Electrical and Information Engineering, Shaanxi University of Science & Technology, Xi′an 710021, China)

According to the existing problems of battery charging and discharging device,a battery charging and discharging system with bidirectional energy flow is designed in this paper.The pre-stage adopts a three-phase PWM rectifier and the last stage adopts a Buck-Boost bidirectional DC/DC converter.The combined control strategy of pre and post stages is studied according to the method of charging and discharging.The battery constant current, constant voltage,charge control and discharge control are achieved. Using PLECS software to simulate and the simulation results show that the system has high power factor and low total harmonic distortion.

charging and discharging; bidirectional energy flow; PWM rectifier; Buck-Boost converter

2016-10-16

陕西省科技厅工业科技攻关计划项目(2015GY173)； 西安市科技计划项目( CXY1513(5))

史永胜(1964-)，男，陕西西安人，教授，博士，研究方向：特种电源和先进光电器件

1000-5811(2017)01-0151-07

TM461

A