“随机”与“择优”——超网络演化的内在驱动力

索 琪， 郭进利(.上海理工大学管理学院，上海 200093；2. 青岛科技大学经济与管理学院，山东 青岛 26606)

“随机”与“择优”
——超网络演化的内在驱动力

索 琪1,2， 郭进利1
(1.上海理工大学管理学院，上海 200093；2. 青岛科技大学经济与管理学院，山东 青岛 266061)

基于“随机连接”和“择优选择”的演化机制，构建了一个随机-择优混合超网络演化模型。使用Poisson 过程理论和连续化方法对模型进行分析，获得超度分布的解析表达式，分析表明网络的稳态平均超度分布服从漂移的幂律分布。该模型可以退化到复杂网络和超网络中的标准模型，具有一定的普适性。通过调节机制系数，模型可以体现混合连接机制。并对3个实证数据进行了分析，该模型能有效刻画不同数据的演化机理。

复杂网络；超图；超网络

0 引言

1999年，Barabási通过对社会、经济、技术等大量系统统计发现，多数复杂网络的度分布服从幂律分布。他们提出了经典的BA模型，认为增长和择优连接机制是驱动这种无标度网络演化的重要机制[1]。此外，他们认为当新节点随机连接老节点时，度分布呈指数分布。此后，在BA模型的基础上，学者建立了各种网络模型刻画网络的拓扑性质及演化机理。复杂网络基于普通图的拓扑结构，即用节点代表实际系统中不同的个体，用连边代表节点之间的关系，且一条连边只能关联2个节点。但是，现实网络的很多特征无法用它全面有效地描述[2]。如科研合作网络只能描述两两作者之间的合作情况。此外，文献[3]讨论了含有用户、商品以及标签3类节点的推荐系统，普通图很难刻画这种多元关系。Berge[4]给出了超图理论的基本概念和性质，由于超图中的一条超边可以包含多个节点，基于超图理论的超网络能够更有效地描述各个节点之间的相互作用和影响。如将作者视为节点，由若干个作者共同合作完成的论文视为超边，可以构建科研合作超网络。基于该超网络可以获得一篇论文是否由3个或更多的作者合作完成、以及每个作者发表的论文数量等信息。如供应链超网络中，将供应商、制造商和消费者等视为节点，商贸对象之间存在的一次供需合作关系对应于一条超边，可描述不同类型实体之间的多元合作关系。可见，超网络方法作为一种全面、准确描述现实网络的重要工具，必然引发未来的研究热潮。

对复杂系统进行建模可以有效揭示其内在演化机理。目前，学者针对超网络动态演化模型提出了不同的构建方法。Zhang等[5]建立了一种基于用户背景知识和对象、标签双重优先连接机制的超图增长模型。裴伟东等[6]研究了基于一类三角形结构的动态网络演化模型，利用平均场方法给出了这一类网络结构的理论解。基于增长和择优连接机制，Wang等[7]构建的模型每次进入m个新节点，选择1个老节点结合生成超边；Hu等[8]构造了另一类动态演化模型，每次进入1个新节点，选择m个老节点生成超边。上述两个模型每个时间步只增加一条超边。Yang等[9]探讨了基于超边增长和局域世界择优连接机制的超网络演化模型。文献[10]在超网络中建立了一个将文献[7]、[8]中的模型及BA模型统一的无标度模型。文献[11]建立了非线性择优连接的非均齐超网络演化模型。

现有超网络模型的共同特点是基于“点超度择优”机制，即择优概率与被选节点的超度成正比。新节点倾向于连接到超度较大的节点，这种择优连接机制导致老节点的平均超边数必然高于新节点，导致了“富者越富”现象。然而，很多真实网络并未展现出幂律分布特征，因此其演化过程并不能很好地用上述机制描述。实际网络中有些个体之间的连接是完全随机的，Liu等[12]最早在复杂网络中提出了随机和择优混合模型，随后学者也相继研究了和随机连接相关的演化模型[13-15]。能否构建一个超网络演化模型，考虑到超网络演化过程中的随机连接和择优选择的增长机制，使得模型与实际网络更好地吻合；并研究随机概率对网络结构的影响，为真实网络的演化过程提供某种解释，是本文关注的重点。

1 随机-择优混合超网络演化模型

1.1 超网络的概念

1.2 模型的构造

随机-择优混合超网络模型满足如下规则：

1) 初始化。网络开始时有较少的节点(m0)，这m0个节点形成一条超边。

2) 网络增长。现存文献假设节点在等时间间隔离散地进入系统，为获得网络的统计信息，其研究中包含连续性假设，即将离散问题连续化。由于现实世界中网络的增长是连续的，因此采用节点按Poisson过程随机增长的网络可以更好地刻画现实。假设节点的到达过程是具有常数为λ的Poisson过程。在时刻t，当一批新节点(m1个)进入网络时，这m1个新节点与已经存在的m2(≤m0)个老节点形成一条超边，共形成m(≤m0)条超边，且不出现重超边。

3) 连接机制。新节点在选择网络中已有的节点i时，以概率p随机连接；以概率1-p依据超度择优连接，即老节点i被选中的概率W为

(1)

其中，ti表示第i批节点进入网络的时刻，hj(t,ti)表示第i批进入的第j个节点在时刻t的超度，n(t)表示时刻t网络中的节点数。以科研合作超网络为例，将作者视为节点，由若干个作者共同合作完成的论文视为超边。节点的超度越大，代表该作者参与撰写的论文越多。点超度大的节点可能是本领域的专家，当新的作者进入网络时会倾向于与专家合作，以提高自身的知名度，这体现为式(1)右端的第一项，即择优连接。另一方面，新的作者也可能以一定的概率随机从网络中选择几个作者进行合作，这体现为式(1)右端的第二项，即随机连接。

2 演化模型理论分析

记N(t)={时刻t网络的节点数}-m0=n(t)-m0， 根据Poisson过程理论，E[N(t)]≈λt。假定hj(t,ti)是连续实值变量，由于hj(t,ti)的变化率正比于概率W(hj(t,ti))，从而，由连续化方法可知hj(t,ti)满足动态方程

(2)

(3)

由于hj(ti,ti)=m，解方程(3)，得

(4)

由式(4)，有

(5)

由Poisson过程理论，节点的到达时间ti服从参数为i与λ的Gamma分布Γ(i,λ)，有

(6)

将式(6)带入式(5)，得：

(7)

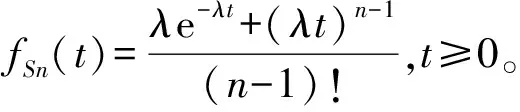
(8)

由式(8)可知，该超网络演化模型的稳态平均超度分布为

(9)

(10)

文献[15]提出了漂移的幂律分布(Shiftedpowerlaw，SPL)的概念，即P(k)∝(k+α)η，其中η和α是常量。SPL分布是介于指数函数和幂律分布之间的一种分布，α代表了该分布偏离幂函数的程度，α越大越偏离幂函数。由式(10)可知，随机-择优混合超网络演化模型的稳态平均超度分布服从漂移的幂律分布。

当λ=m1=m2=1时，该超网络模型退化到复杂网络的混合模型。

当p→1时，α→∞，该超网络模型的超度分布趋向于指数分布。由式(1)可知，此时的连接机制为完全随机连接，导致了点超度呈指数分布。

当p介于0和1之间时，由式(1)可知，“随机连接”和“择优选择”两种机制共同驱动了超网络的演化。p值越大，“随机连接”的驱动机制更明显，点超度越趋向于指数分布；反之，“择优选择”的驱动机制更明显，点超度越趋向于幂律分布。通过调节参数p，超网络模型的演化动力机制中的3种趋势：随机连接、择优选择、以及两者之间的混合连接机制可以体现出来，可以获得具有特定超度分布的超网络演化模型，因此该模型具有较强的适用性。

3 实证数据分析

3.1 电视节目竞争超网络

数据来源于中央电视台官方网站(http://cctv.cntv.cn，http://tv.cntv.cn/epg)。以中央电视台的为例，为抢占收视率市场，在同一时间段播出的电视节目之间存在着激烈的竞争关系。由于每周播出的电视节目相对稳定，因此以周为单位可以更完整地分析电视节目超网络的整体特点。为方便统计，以2h为一单位对每天的播出时间离散化处理，分段初始点从周一0点开始，结束点为周日的22点，一周共分为84个播出时间段。基于15个中文频道的227个播出时间相对稳定的节目数据分析。将播出时间段定义为超边，则该超网络含有84条超边；将电视节目定义为节点，则含有227个节点。电视节目在某个时间段播出，则称该节点包含于该超边中。

点超度的大小反映了一个节目在一周内的播出次数，统计结果表明平均点超度为6.5，即平均每个节目每周播放6.5次。获得点超度的累计分布如图1所示，对数据进行SPL拟合，p(k)∝(x+45.78)-8.49，即α=45.78,p=0.77。说明驱动电视节目超网络演化的因素既有择优机制，又有随机机制。新节目进入网络时，以概率0.23进行择优选择，以概率0.77随机连接。这与现实情况相吻合，由于黄金时段的收视率高，新的电视节目进入网络时，会优先考虑在黄金时段播出，即与该超边所包含的节点构成择优连接关系。但是，如果完全采用择优方式连接，这样的网络会存在弊端，会出现很多节目在黄金时段播出，而很多时段没有节目播出的情况，这是不符合实际的，也无法从总体上满足观众的收视需求。在电视节目的实际编排中，会根据电视观众的特征、收视的时间规律及收视内容偏好，采取差异化的节目编排策略，进而全天候满足不同观众不断变化的收视需求。由于需要考虑的具体因素较多，节点之间的关联相当于随机选取。在这种混合的连接机制驱动下，可以获得相对均匀的节目编排。

3.2 国内电影演员合作超网络

数据来源于Mtime时光网(http://www.mtime.com/)，以国内电影为检索词，获得了8 480部电影信息，及其主演信息。将电影定义为超边，则该超网络含有8 480条超边；将演员定义为节点，则含有9 007个节点。如果该演员参演了某部电影，则称节点包含于超边中。点超度分布如图2所示，对数据进行SPL拟合，p(k)∝x-2.08，即α=0,p=0，说明驱动该超网络演化的机制是完全择优连接。这种机制导致点超度分布服从幂律分布。由图2可见，数据存在明显的胖尾现象，说明演员参演的电影数量是非均匀的。即大部分演员只参演了较少的几部电影，而只有少量演员参与了多部电影的演出。网络中最小点超度为1，最大点超度为82。平均点超度为2.56，即平均每个演员参演了2.56部电影。点超度大的节点代表该演员参与了多部电影的演出，对应于知名演员。在演员合作超网络的演化过程中，当新演员进入网络参演电影时，为了提高影片的票房，一般会选择知名演员合作，利用其良好的口碑提高电影的竞争力；而知名演员也获得了更多的参演机会，导致了“富者越富”现象。

3.3 豆瓣数据评论超网络

豆瓣是中国最大的在线社交网站 (http://www.douban.com)之一，该网站允许注册用户描述其消费体验，用户可以对其体验(或正在体验)的资源 (包括图书、电影、音乐等)进行评分和评论，也可以阅读到其他用户的信息和评论状态。数据集记录了383 033个用户对80 008本图书的评论数据，共3 648 105条记录。将用户定义为节点，将图书评论关系定义为超边，如果某个用户对某本图书进行了评论，则称该节点包含于超边中。点超度分布如图3所示，对数据进行SPL拟合，p(k)∝(x+3.19)-2.59，即α=3.19,p=0.13。由图3可见，数据存在明显的胖尾现象，即用户参与评论的图书数量具有明显的异质性，大部分用户只阅读和评论了较少的图书。最小点超度为2，最大点超度为4 110。平均点超度为9.52，说明每个用户参与评论的平均图书数量为9.52。驱动该超网络演化的因素既有择优机制，又有随机机制。新用户进入网络时，以概率0.87进行择优选择，以概率0.13随机连接。说明用户在选择图书时，会优先选择一些优质图书或畅销图书阅读并评论，即与参与评论该图书的用户形成了择优选择关系。此外，用户还会根据自己的兴趣爱好选择图书阅读并评论，与网络中的老用户随机连接。这两种混合机制共同驱动了超网络的演化。

上述3个实证结果显示，超度分布均可以用式(10)中的漂移的幂律分布形式拟合，分布参数的大小可以表示出分布结果的不均匀性，也揭示了驱动超网络演化的根本机制。

4 总结与展望

本文构建了随机-择优混合超网络演化模型。对真实网络研究发现，新节点在选择老节点连接时，既存在择优选择，又存在随机连接的情形。因此，在连接机制的设置上，点超度择优和随机选择是驱动网络演化的两个重要因素。该连接机制可以更好地反映节点在竞争环境中的演化规律，能够更真实地反映节点间竞争获得超边的本质特点。通过理论分析发现了随机-择优混合超网络的演化规律，获得稳态平均超度分布的解析结果。通过合适的参数选取，模型可以退化到复杂网络中的混合模型和超网络中的无标度模型，该特性显示了模型的普适性。同时，该模型也能有效刻画实证数据的演化机理。

目前对于超网络的拓扑特征和演化机制的研究刚刚起步。现有研究简化了节点和超边的关系和特征，对于超边带有边权的加权超网络、节点间连边关系具有方向的有向超网络、带有寿命的节点老化超网络、以及考虑退出机制的超网络等问题都是未来亟待解决的研究方向。

[1]Barabási A L, Albert R. Emergence of scaling in random networks [J]. Science, 1999, 286 (5439): 509-512.

[2]王众托. 关于超网络的一点思考[J]. 上海理工大学学报, 2011, 33(3): 229-237. Wang Zhongtuo. Reflection on supernetwork [J]. University of Shanghai for Science and Technology, 2011, 33(3):229-237.

[3]Lü L, Medo M, Yeung C H, et al. Recommender systems [J]. Physics Reports, 2012, 519(1): 1-49.

[4]Berge C. Graphs and Hypergraphs[M]. Amsterdam: North-Holland Publishing Company, 1973.

[5]Zhang Z K, Liu C. A hypergraph model of social tagging networks [J]. Journal of Statistical Mechanics: Theory and Experiment, 2010, (10): P10005.

[6]裴伟东, 夏玮, 王全来，等. 多三角形结构动态复杂网络演化模型及其稳定性分析[J]. 计算机工程与应用, 2011, 47(23): 41-44. Pei Weidong, Xia Wei, Wang Quanlai, et al. Study of dynamic complex network evolving models with multi-triangular structure [J].Computer Engineering and Applications, 2011, 47(23): 41-44.

[7]Wang J W, Rong L L, Deng Q H, et al. Evolving hypernetwork model [J]. The European Physical Journal B-Condensed Matter and Complex Systems, 2010, 77(4): 493-498.

[8]胡枫, 赵海兴, 马秀娟. 一种超网络演化模型构建及特性分析[J]. 中国科学, 2013, 43(1): 16-22. Hu Feng, Zhao HaiXing, Ma XiuJuan. An evolving hypernetwork model and its properties [J]. Scientia Sinica:Physica, Mechanica & Astronomica, 2013, 43 (1): 16-22.

[9]Yang G Y, Hu Z L, Liu J G. Knowledge diffusion in the collaboration hypernetwork [J]. Physica A: Statistical Mechanics and its Applications, 2015, 419: 429-436.

[10] 郭进利, 祝昕昀.超网络中标度律的涌现[J]. 物理学报, 2014, 63(9): 90207. Guo Jinli, Zhu Xinyun. Emergence of Scaling in Hypernetworks [J]. Acta Physica Sinica, 2014, 63(9): 90207.

[11] 郭进利. 非均齐超网络中标度律的涌现——富者愈富导致幂律分布吗[J]. 物理学报, 2014, 63(20): 208901. Guo Jinli. Emergence of scaling in non-uniform hypernetworks——does “the rich get richer” lead to a power-law distribution [J]. Acta Physica Sinica, 2014, 63(20): 208901.

[12] Liu Z, Lai Y C, Ye N, et al. Connectivity distribution and attack tolerance of general networks with both preferential and random attachments [J]. Physics Letters A, 2002, 303(5): 337-344.

[13] Li X, Chen G. A local-world evolving network model [J]. Physica A: Statistical Mechanics and its Applications, 2003, 328(1): 274-286.

[14] Zhang P P, Chen K, He Y, et al. Model and empirical study on some collaboration networks [J]. Physica A: Statistical Mechanics and its applications, 2006, 360(2): 599-616.

[15] Fu C H, Zhang Z P, Chang H, et al. A kind of collaboration-competition networks [J]. Physica A: Statistical Mechanics and its Applications, 2008, 387(5): 1411-1420.

[16] Estrada E, Rodriguez-Velazquez J A. Subgraph centrality in complex networks [J]. Physical Review E, 2005, 71(5): 056103.

[17] Estrada E, Rodriguez-Velazquez J A. Subgraph centrality and clustering in complex hyper-networks [J]. Physica A：Statistical Mechanics and its Applications, 2006, 364: 581-594.

(责任编辑 耿金花)

Both Random and Preferential Attachment—the Inner Motivation in the Evolution of Hypernetworks

SUO Qi1, 2, GUO Jinli1

(1.Business School, University of Shanghai for Science and Technology, Shanghai 200093，China;2. School of Economics and Management, Qingdao University of Science and Technology, Qingdao 266061,China)

An evolving hypernetwork model is constructed with both preferential and random attachment. We analyze the model by using Poisson process theory and a continuous technique, and obtain the stationary average hyperdegree distribution of the hypernetwork. The analytical result shows that the stationary average hyperdegree distribution can be described with “shifted power law” (SPL) function form. Our model is also universal, in that the standard model in complex networks and scale-free model in hypernetworks can all be seen as degenerate cases of the model. By adjusting the parameter, the model can reflect the mixed-connection mechanism. In addition, three empirical data are analyzed, and can be effectively described by the model.

complex network; hypergraph; hypernetwork

10.13306/j.1672-3813.2016.04.007

2014-12-17；

2015-05-14

国家自然科学基金(71571119)；教育部人文社会科学研究项目(16YJC870012)；国家统计科学研究项目(2015LZ49)；青岛市社会科学规划研究项目(QDSKL150462)

索琪(1980-)，女，黑龙江哈尔滨人，博士研究生，讲师，主要研究方向为复杂网络、超网络。

郭进利(1960-)，男，陕西西安人，博士，教授，主要研究方向为复杂网络、人类行为动力学。

T94

A