平面几何最值问题的解法

钱宜锋●

江苏省海安县隆政初级中学(226611)



平面几何最值问题的解法

钱宜锋●

江苏省海安县隆政初级中学(226611)

平面几何最值问题在近几年的中考中更加趋于综合性以及多样性，以平面几何为出题背景，将各方面的知识融入其中是创作此类问题的源泉，也因此成为了中考的重点以及难点所在.多样的解题方法也是此类问题体现出的迷人之处，值得我们探讨.

对称性;不等式;二次函数

平面几何的最值问题多为在存在动点或者不确定的位置关系的情况下求最值，有两种解题思路，一个是通过几何图形的性质实现对位置的确定，另一个是通过数量关系实现最值问题的解答.

一、利用对称性质，实现问题简单化

图形经过某一点或者轴对称之后，就会有很多固有的由对称产生的等量关系，不同的对称性(如中心对称、轴对称等)也有独特的对称性质.合理地利用相应的性质会使问题得到简化，这会给解题带来很大的帮助.

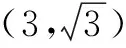
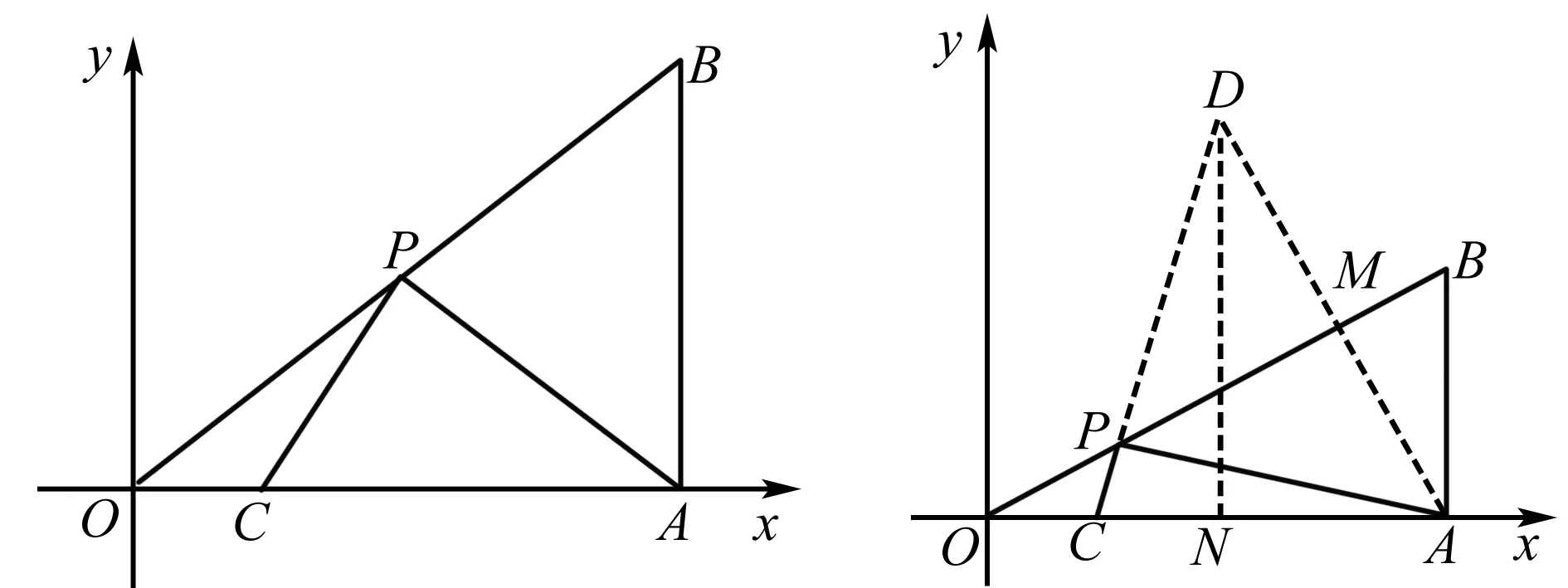
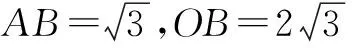
点拨 本题中是作直线的对称点，实现直线同侧点到异侧点的转化，这是我们在解题中常遇到的情况以及常见的解题方法.对称性的应用注重于问题的解题技巧，目的是通过对称性使复杂的问题简单化.

二、构造不等关系，巧用基本不等式

对于平面几何问题，不等关系的构造是离不开几何图形本身的数量关系的.想要利用基本不等式求解，学生需要在图形中找出满足不等式的条件，这不光对于学生的平面几何知识有考查，还要学生深入理解不等式的相关知识.

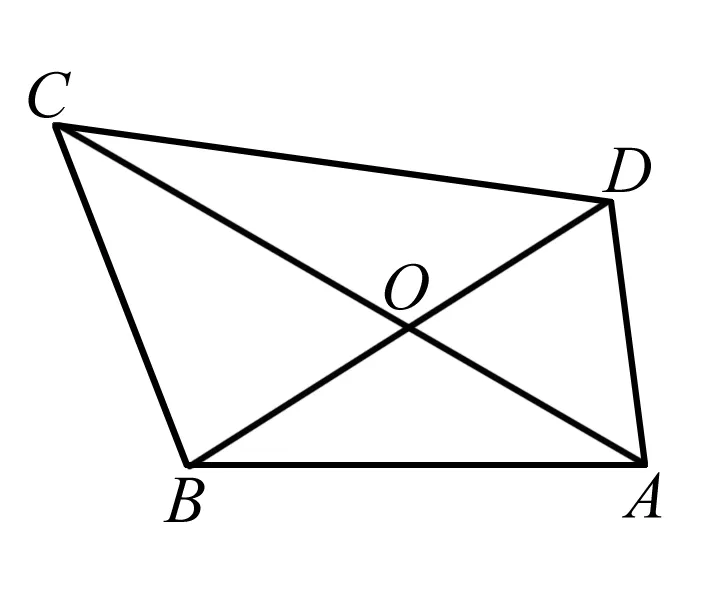
例2 已知四边形ABCD，O点为对角线AC与BD的交点，SΔAOB=4，SΔCOD=9，求四边形ABCD的面积S的最小值

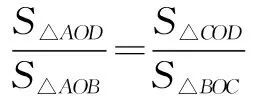
点拨 本题中对于三角形知识的考察非常深入，将三角形面积间的关系转化为长度关系进行解答是最为关键的步骤，学生要有思维模式的转化才会想出这一解决方法，而后结合不等式知识解题，否则盲目地求面积是不能实现的.

三、化为二次函数，列出方程再求解

二次函数是初中数学中最重要的一类函数，此处并不是像压轴题那样对二次函数进行全面的考察，而是将所求的量转化为二次函数的形式，利用二次函数的相关性质解题.更加注重于对问题的分析转化能力.

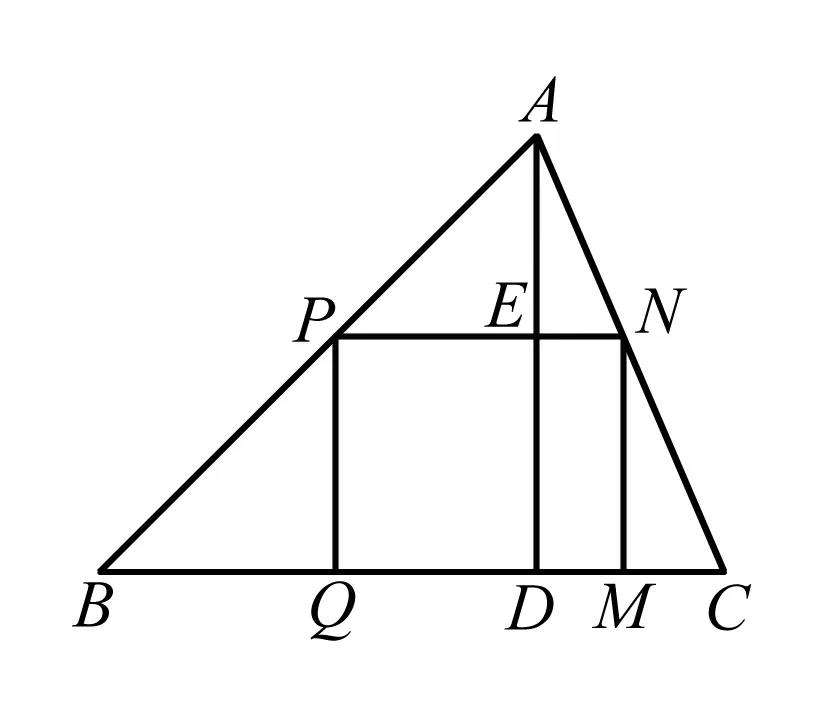
例3 有一三角形ABC，底边BC=120，高AD=80，如图所示，若要在三角形里面画出一矩形，求该矩形面积的最大值.

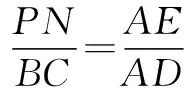
点拨 相似三角形的引入让求线段的长度变得简单得多.本题中对于最后二次函数的配方变形可谓更为直接，让学生更直观地看到函数的最值.

G632

B

1008-0333(2016)35-0010-01