巧借图形性质解与圆有关的最值问题
刘 珍●
江苏省镇江实验学校魅力之城分校(212000)
巧借图形性质解与圆有关的最值问题
刘 珍●
江苏省镇江实验学校魅力之城分校(212000)
作为中考的热点内容,与圆相关的最值问题以其综合性强、难度可调、题型多变等优势成为了最值问题中非常容易出现的情况.而图形性质又是固定的,针对不同的问题利用不同的图形性质是解决此类问题的关键所在.与圆相结合在一起出现的图形常见的就是三角形、矩形等,与线段、直线等有关的性质也可以作为图形的性质看待,掌握了这么多的性质之后,就可以运用不同的方法对圆的最值问题进行求解了.下文就给出三种情况,帮助学生理解.
一、活用垂线段及等腰三角形性质,解决圆中距离问题
垂线段就是某点到某一直线的垂直线段,不论如何点到直线的最短距离就是垂线段的长度.而作为三角形中的特例等腰三角形又有很多的性质.将上述相关性质结合,就可以变为解决一道题的制胜关键.

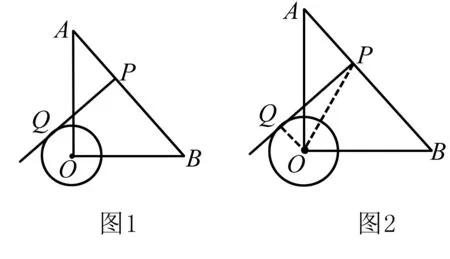

点拨 对于直角三角形高的求法有很多种,利用面积相等法求解是我们必须掌握的.同时题中涉及到的切线以及勾股定理相关知识也是学生必备知识.利用上述几点提到的图形性质学生就可以将本题顺利解决了.
二、利用圆中弦及三角形相关性质解面积最值
求面积最值的问题关键就在于将面积转化为其他问题求解,因为面积的求解一定是有多个量的参与,将其转化成单一变量那就会很大程度地减少计算量以及简化题目的难度,同时利用图形的性质就可以轻松解题.
例2 如图3所示有一半径为2的圆O上存在M、N两动点,且在直线l的异侧,直线交圆O于A、B两点,若 ∠AMB=45°,求四边形MANB面积的最大值.

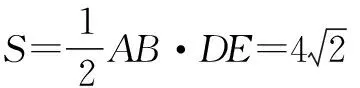
点拨 作为很经典的四边形面积最值问题,我们这里用逻辑思维和常规的解法使问题得到了解决.本题的难点就在于如何实现面积最值的转化,通常此类问题都是不能直接求出的,而本题中正是运用了线段长度代替面积求出的.
三、利用圆的性质解最值问题
与圆有关的最值问题当然离不开圆本身,那么如何利用好与圆有关的性质就是我们需要多加练习的了.
例3 如图5所示,AC垂直圆O的直径AB于点A,BD垂直AB于点B,P为圆上一动点,若AB=2,AC=2,BD=3,分别求△PCD的面积的最大值和最小值.

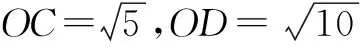
点拨 本题中的情况是出题者有意安排的,OC恰好垂直于CD,而此种情况也为接下来的计算和理论分析带来了一定的方便,学生要观察出此处的隐含的垂直条件,同时利用圆本身的长度性质解题也是本题中的巧妙之处.
三道不同的题目从不同方面反映出图形性质的多样性,掌握并学会利用各种类型的图形有利于对与圆有关的最值问题的解答,同时也是学生必须熟记的知识,不光是此类问题的求解,对于平面几何证明题等多种类型的题目都是有很大好处的,希望学生可以灵活运用,学会举一反三,最终达到自身解题能力的提升.
G632
B
1008-0333(2016)35-0011-01

