利用(G/G,1/G)-展开法求解非线性Schrodinger方程
王文君●
广州大学数学与信息科学学院(510006)
利用(G/G,1/G)-展开法求解非线性Schrodinger方程
王文君●
广州大学数学与信息科学学院(510006)
非线性Schrodinger方程是数学物理中一类重要的非线性演化方程,在量子力学,非线性光学电磁学等众多领域中得到广泛应用,故对Schrodinger方程研究有着重要的物理意义.本文应用(G/G,1/G)-展开法对Schrodinger方程进行精确解求解,并讨论了解与方程的系数关系.
(G/G,1/G)-展开法; 非线性Schrodinger方程; 精确解
2. (G/G,1/G)-展开法的基础公式
在(G/G,1/G)-展开法中,考虑二阶线性常微分方程:
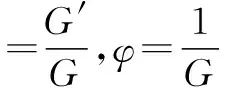
由此得到:φ′=-φ2+μφ-λ,φ′=-φφ.
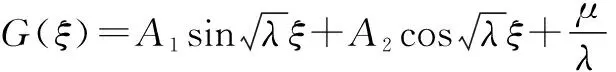
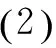
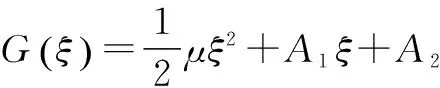
3.非线性Schrodinger方程的求解
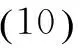
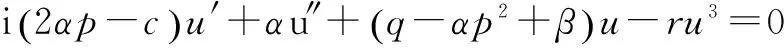
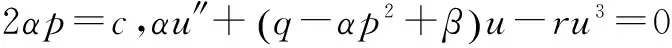
得到非线性ODE方程u″+k1u+k2u3=0,
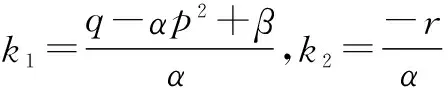
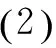
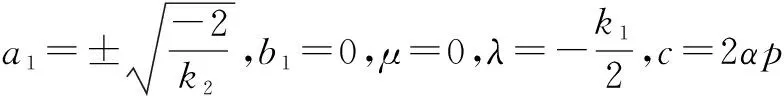
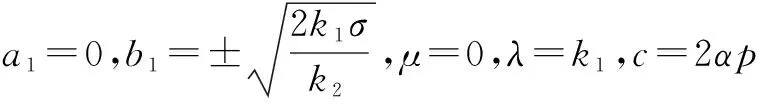
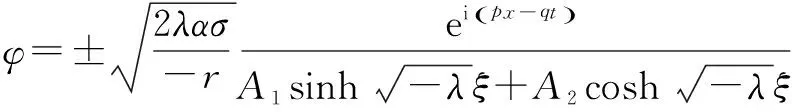
(17)
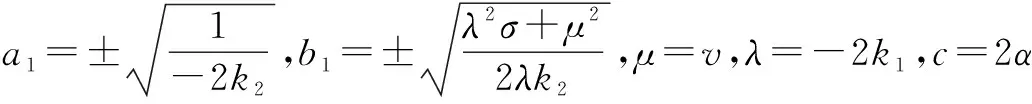

情形2 当λ>0时,类似情形1,由(G/G,1/G)-展开法得基础公式求解得:
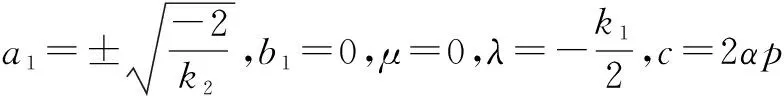
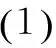
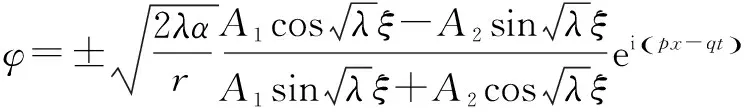
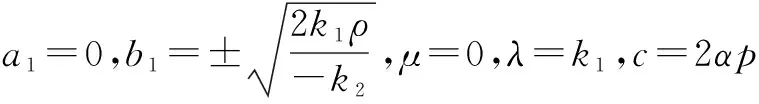
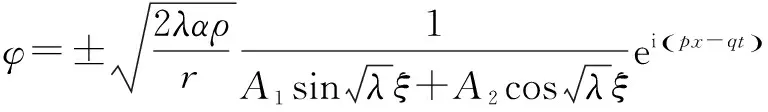
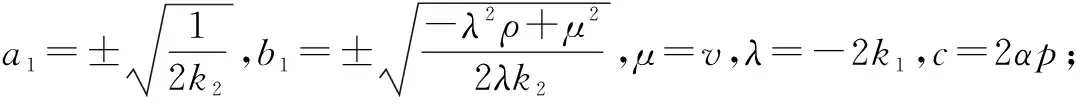
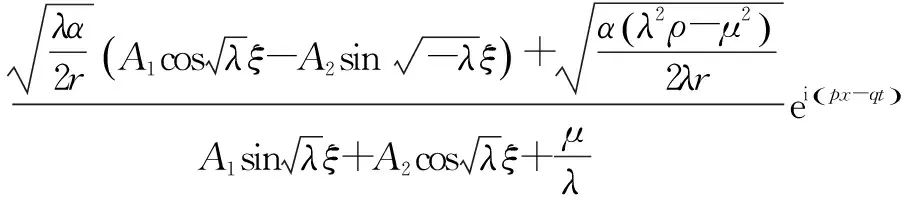

情形3 当λ=0时,类似情形1,由(G/G,1/G)-展开法得基础公式求解得:
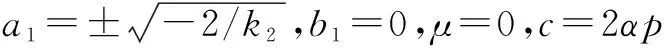
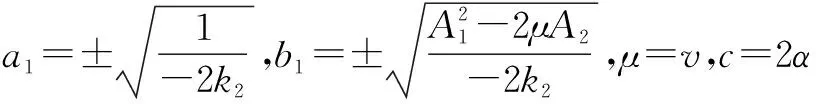
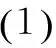

4 结论
利用(G/G,1/G)-展开法求得了非线性Schrodinger方程多种类型的含有任意参数的精确行波解,其中包括双曲函数形式、三角函数形式和有理函数等各种形式的精确解,并与以往文献相比,出现的新形式行波解将对复杂的物理现象的解释起到一定的借鉴作用.
[1]Hirota R. Exact solution of the Korteweg-de Vires equation of multiple collision of solitons. Physical Review Letters.27(1971)1192-1194
[2] Shang YD. The extended hyperbolic function method and exact solution of the long-short wave reasonance equation. Chaos, Solitons and Fractals.36(2008)762-771
[3]He J H,Wu X H.Exp-function Method for Nonlinear Wave Equations [J].Chaos,Solutions & Fractals,2006,30:700-708.
[4] Li LX, Li EQ, Wang ML. The(G/G,1/G)-expansion method and its application to travelling wave solutions of the Zakharov Equations. Appl Math J Chinese
Univ.25(2010)454-462.
G642
B
1008-0333(2016)36-0003-02

