线性延迟微分方程的一类新解法
——再生核数值解
杜 萍● 张 虹● 郑丽伟●
山东工商学院(264005)
线性延迟微分方程的一类新解法
——再生核数值解
杜 萍● 张 虹● 郑丽伟●
山东工商学院(264005)
线性延迟微分方程在生物学、物理学等领域具有越来越广泛的应用,本文通过再生核构造一个新的方法,对此类方程提供了一种新的方法.
线性延迟微分方程;再生核;精确解;数值解
客观事物的变化是多种多样的,有些变化不仅依赖于当前的状态,还与它的历史因素有很大关系,一般来说,都存在一点滞后的影响,本文主要针对线性延迟微分方程给出一种新的解法,验证再生核方法来解决线性延迟微分方程的可行性,如下面的方程:
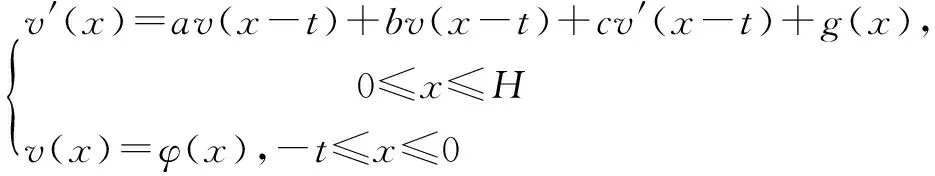
(1.1)
其中0 Rx(t)=1/(2sinh(H))[cosh(x+t-H) +cosh(|x-t|-H)] 对任给的t∈[0,H],有关于x的函数(或对于任给的x∈[0,H],有关于t的函数)R(x,t)。能得出Rx(t)有下面的结论: 引理Tv(s)=〈v(y),TSRy(s)〉y,这里Ts表示算子T对变量s的作用,那么(1.1)可以写成v(t)=Tv(t)+f(t). 而又知〈u(t),φj(t)〉=f(tj), 〈φi(t),φj(t)〉t =Rti(tj)+KRtj(t)|t=ti+KRti(t)|t=tj+K[KRt(s)|s=tj]|t=ti 从而 文章主要是为线性延迟微分方程的求解提供了一种简单有效的思路,在实际的计算中,为了简化运算,一般使用MATHMATIC或者是MATLAB进行编程,通过试验,我们得到步长与误差成正比,若步长小,则理论值和精确值差别越小,越精确。这也就说明了这种算法是可行的。 项目来源:校青年基金项目2014QN024 [1]杜萍.延迟微分方程的再生核数值解法,哈尔滨工业大学. G642 B 1008-0333(2016)36-0002-01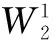

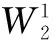
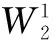
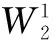
二、实例

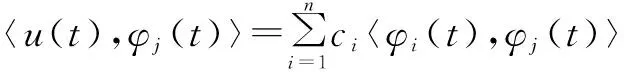
三、总结

