基于社交网络结构的节点影响力度量方法
李泽鹏,左 杨,王宏宇
(1.北京大学高可信软件技术教育部重点实验室,北京 100871;2.北京大学信息科学技术学院,北京 100871)
基于社交网络结构的节点影响力度量方法
李泽鹏1,2,左 杨1,2,王宏宇1,2
(1.北京大学高可信软件技术教育部重点实验室,北京 100871;2.北京大学信息科学技术学院,北京 100871)
度量社交网络节点影响力是社交网络结构分析的关键问题之一.目前研究社交网络节点影响力的方法主要有两大类:中心度方法和节点删除方法.前者主要通过度或最短路径等因素来判断节点的影响力,不考虑网络的连通性;后者通过节点删除后对网络结构的破坏程度来判断,计算复杂性很高,不适用于较大规模的社交网络.通过结合社交网络的局部连通度及节点间的最短路径,提出了连通中心度来度量社交网络中节点的影响力,并给出了连通中心度的计算方法和一些特殊网络中节点的连通中心度的值.最后,通过实验说明该指标能很好地度量社交网络中节点的影响力.
社交网络;节点影响力;中心度方法;连通中心度;最短路
1 引言
社交网络的拓扑结构是网络各项功能实现的基础,对社交网络的拓扑结构、功能及其之间的关系目前已有大量研究[1~3].分析社交网络的拓扑结构,一个主要的方法是挖掘社交网络中有重要影响力的节点,这些节点对社交网络的信息传播、网络结构的演化起着关键的作用[4,5].因此,如何度量节点的影响力,如何在社交网络中发现这些重要节点是研究社交网络结构及功能的关键.
目前刻画社交网络节点影响力的方法主要有两大类:一类是中心度方法,如度中心度[6]、紧密中心度[7]、介数中心度[8]、特征向量中心度[9,10]等;另一类是节点删除方法,即通过度量节点删除后对社交网络的破坏程度来确定节点影响力的方法.
中心度方法主要是通过社交网络中节点的度或节点间最短路径等因素来判断社交网络中节点的影响力,计算复杂程度较低,因此这类方法被广泛应用于社交网络的结构分析技术中[11].
度中心度的方法是通过节点在社交网络中度的大小来确定节点的影响力,即通过每个节点的邻居节点数来判断,其优势是计算代价小,可应用于大规模网络中.但是,节点度的大小只能体现社交网络结构的一个局部性质,所反映的是节点与其邻居节点之间的关系,无法判断节点在整个社交网络中的影响力.为此,Chen等人[12]在度中心度的基础上,进一步提出了局部中心度的方法来度量节点在社交网络中的影响力.节点v的局部中心度CLOC(v)定义为:
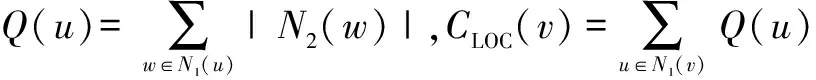
其中Ni(u)表示到节点u的距离不超过i的所有节点构成的集合,i=1,2.局部中心度实际上是度中心度的推广,节点v的局部中心度受到与v的距离不超过4的所有节点的影响,并且与v的距离越小对其影响越大.
紧密中心度和介数中心度方法主要是通过社交网络中最短路径来刻画节点的影响力.节点v的紧密中心度CCLO(v)为:
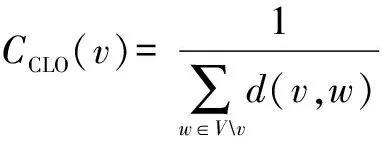
其中d(v,w)表示节点v到节点w的距离,即它们之间的最短路径的长度;节点v的介数中心度CBET(v)定义为:
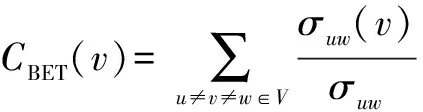
其中σuw表示节点u与节点w之间最短路的条数,σuw(v)表示这些最短路中经过节点v的条数.可以看出,紧密中心度所反映的是节点在社交网络中的居中程度,节点的紧密中心度越大,说明此节点到其他节点的平均距离越小,即从此节点到其他节点的信息传播越快,也就间接地表示该节点在社交网络中的影响力越大.而介数中心度反映的是节点在社交网络拓扑结构中位置的重要性,是对其他节点之间信息传播影响的一种度量指标.节点的介数中心度越大,说明社交网络中信息传播时经过该节点的信息量越大,即表示该节点在社交网络中的影响力越大;反之也就越小.
特征向量中心度的方法主要是利用随机游走的特征来判断节点的重要程度.节点的特征向量中心度定义如下:
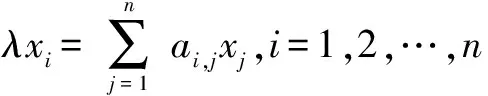
其中λ表示邻接矩阵的最大特征值.特征向量中心度所反映的是节点的影响力与其邻接节点的影响力相关,特别是与游走路径上其他节点的影响力相关,其他节点影响力越大,当前节点的影响力也就越大,反之就越小.
另一类度量社交网络中节点影响力的方法是节点删除方法,主要通过刻画节点删除后对社交网络结构的破坏程度来判断节点的影响力,其考虑到社交网络的整体连通程度,这类方法更多的是应用在系统科学领域的研究中,主要理论有网络的坚韧集与坚韧度以及核与核度等.
对一个社交网络图G=(V,E),若节点子集S⊂V满足G-S不连通,则称S为G的一个节点割集.记C(G)为G中所有节点割集构成的集合;对一个节点割集S,记ω(G-S)为G-S的连通分支的数目.网络图G的坚韧度τ(G)[13]定义如下:
(1)
且将满足式(1)的节点割集S*称为G的坚韧集.网络图G的核度h(G)[14]定义如下:
h(G)=max{ω(G-V′)-|V′|:V′∈C(G)}
(2)
且将满足式(2)的节点割集S*称为G的核.
图的核度最初被称为离散数[15].Jung[15]提出图的离散度是用于研究图的Hamilton性问题的.此后,许进等[14]将图的离散数引入到系统以及网络的研究中,并形象地称其为系统的核度.
从上述两个定义可以看出,社交网络图的坚韧度与核度都是根据节点割集的阶数和删除这个节点割集后的网络的连通分支数来定义的,均是刻画社交网络整体连通程度的指标.不同的是,根据图的坚韧度来判断时,坚韧度越大,说明连通性越好;但根据核度来判断时,核度越小其连通性越好.相应地,坚韧集与核均是刻画对网络具有重要的或支配性的节点(或节点集)的指标,反映的是社交网络的整体性质,无法对同一个网络中不同节点之间的影响力作出判断.而且,在应用坚韧度或核度来判断社交网络连通性及稳定性时,计算量非常大,不适用于较大规模的社交网络.对社交网络中节点影响力,特别是在线社交网络中节点影响力度量方法和模型的详细介绍可参见文献[16,17].
最近,仍有许多学者研究社交网络的节点影响力.Ma,Ren和Ye等[18]提出了基于资源分配动态和k-层分解的节点影响力度量方法.Saito,Kimura 和Ohara等[19]提出了基于信息传播的节点影响力度量方法,称为超级传递者.Hu和Liu[20]结合特征向量中心度、介数中心度、紧密中心度、度中心度以及相互信息等因素,提出了基于线性判别分析的多指标算法.Kim和Anderson[21],Kas,Wachs和Carley等[22],Gao,Shi和Chen[23]研究了动态社交网络下的节点影响力度量方法.另外,关于社交网络影响力最大化的研究,可参见文献[24~29].
本文在中心度方法与节点删除方法的基础上,提出了一种新的度量社交网络中节点影响力的参数:连通中心度.这个参数结合了节点在社交网络结构中位置的重要性以及对其他节点之间的局部连通度的影响力.
2 连通中心度
在本文中,用图G=(V,E)表示社交网络的拓扑结构,其中V表示节点集,E表示边(连接)集.若无特别说明,均指无向图.记n=|V|为G的节点数,m=|E|为G的边数.
对图G=(V,E)中的两个不相邻的节点vi与vj,若节点子集S⊂V满足在G-S中节点vi与vj不连通,则称S为vi与vj的一个分离集.用c(vi,vj)表示G中节点vi与vj的最小分离集中节点的数目,称c(vi,vj)为节点vi与vj的局部连通度.记
C(vi,vj)={v∈S:S是vi,vj的分离集且|S|=c(vi,vj)}.
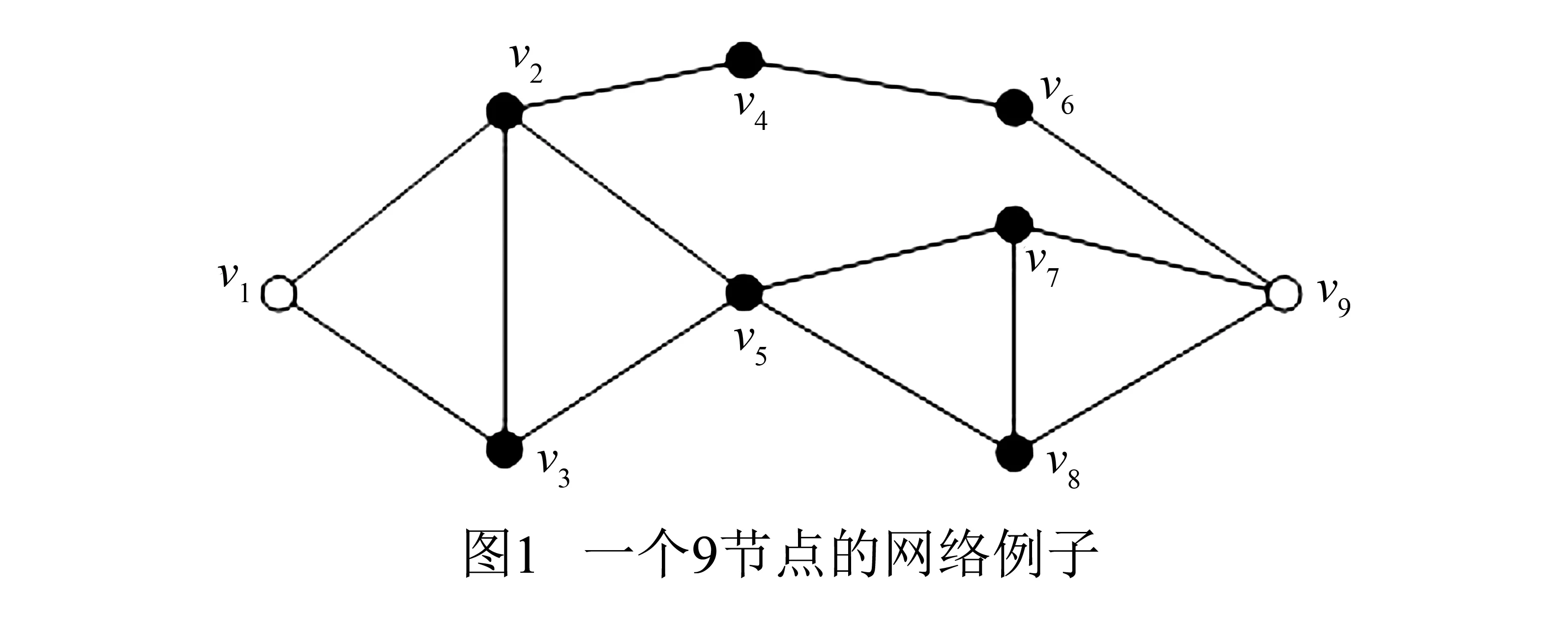
例如,在图1中,S={v4,v5}是节点v1与v9的一个分离集;S={v6,v7,v8}也是节点v1与v9的一个分离集;并且,节点v1与v9的局部连通度为2,C(v1,v9)= {v2,v3,v4,v5,v6}.
用p(vi,vj)表示G中节点vi与vj之间内部互不相交的路的最大条数.Menger[30]证明了c(vi,vj)与p(vi,vj)有如下关系:
定理1[30]设G=(V,E)是一个图,vi与vj是G中不相邻的两个节点,则有c(vi,vj)=p(vi,vj).
2.1 连通中心度的定义
定义1 连通中心度.对一个图G=(V,E),vi,vj是G中的两个不相邻的节点,任意节点vt∈V{vi,vj}对vi,vj的影响力定义为
其中σij表示节点vi与vj之间最短路的条数,σij(vt)表示这些最短路中经过节点vt的条数.当vi,vj在G中相邻时,定义φij(vt)=0.
节点vt的连通中心度定义为vt对G中所有的节点对vi与vj的影响力之和,即

特别,如果G-vt是一个完全图,即G-vt中任意两个节点是相邻的,则定义CCON(vt)=0.
由定义1可知,对G中的任意两个不相邻的节点vi,vj以及vt∈V{vi,vj},有
0≤φij(vt)≤1.
若φij(vt)=0,则vt不在vi与vj的任何一个分离集中,也不在它们的最短路上,即说明在网络G中,节点vt对vi,vj没有影响;若φij(vt)=1,则节点vt分离vi与vj或节点vi与vj的任意最短路必经过节点vt,说明在网络G中,节点vt对vi,vj的影响很大.
连通中心度既考虑了经过节点的最短路径的数目,也考虑了此节点对其他节点对的局部连通性,是一个从网络整体出发度量节点影响力的指标.节点的连通中心度越大,说明此节点对整个网络的影响越大,重要性越高.反之,连通中心度越小,对网络的影响越小,重要性越低.
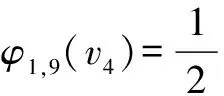
2.2 连通中心度的性质
在一个社交网络中,节点的连通中心度反映的是当前节点对其他节点相互交往过程中的影响力.连通中心度的大小受到社交网络结构的限制.下面根据网络的结构,分析连通中心度的性质.
根据定义1,如果节点v是G的叶子节点,那么vt对其余节点的影响力为0,即有:
性质1 设节点v是网络图G的叶子节点,则CCON(v)=0.
性质2 设G是包含n个节点的完全图,则根据定义1可知,G中任意节点v的连通中心度为CCON(v)=0.
通过性质1和性质2可以看出,一个节点在社交网络中的影响力与其度的大小没有必然的联系,而与网络的整体结构或局部结构关系紧密.在性质1与性质2的基础上,可得到更一般的结论.
性质3 设v是网络图G的一个节点,v在G中的所有邻居节点构成的集合记为N(v),若N(v)在G中的导出子图是一个完全图,则CCON(v)=0.
通常,在一个规模较大的网络中存在很多节点具有相同的影响力,下面给出判断两个节点具有相同连通中心度的一个充分条件.
性质4 设v,w是网络图G中的两个节点,若G-v与G-w是同构的,则节点v与节点w的连通中心度相同,即有CCON(v)=CCON(w).
2.3 连通中心度的计算
对一个图G=(V,E),分别用n=|V|和m=|E|表示G的节点数和边数.对G中的任意节点vt,计算vt的连通中心度最直观的方式就是对每一对不相邻的节点vi,vj计算出φij(vt),然后将所有的非相邻节点对的值进行求和计算出CCON(vt),具体的计算步骤如下:
(1)需要计算G中每对不相邻节点vi,vj间的内部互不相交的路的条数,即计算vi,vj的局部连通度,以及vi,vj之间最小节点割集的并构成的集合C(vi,vj).Ford 和Fulkerson[31,32]给出了一种利用最大流-最小割的方法来计算不相邻节点的局部连通度.利用这种方法,Edmonds和Karp[33]给出一个时间复杂度为O(n·m2)的算法;对边稠密的网络,可利用Goldberg 和Tarjan[34]提出的relabel-to-front算法,其时间复杂度为O(n3).
(2)需要计算每对不相邻节点间最短路经的条数.Floyd[35]给出了在一般图中复杂度为O(n3)的算法,而对边稀疏的网络,Johnson[36]给出了一个时间复杂度为O(n2logn+nm)的算法.
(3) 根据定义1,计算节点vt∈V{vi,vj}对节点对vi,vj的影响力.
(4) 计算出节点vt的连通中心度CCON(vt).
综上可知,通过上述算法计算图G中任意节点vt的连通中心度CCON(vt)的时间复杂度为O(n3),其中n为G的节点数.
以图1所示的9个节点的网络G为例,下面计算每个节点vt的连通中心度.G中任意不相邻的节点对vi,vj的局部连通度、最短路的条数以及最小节点割集的并构成的集合见表1.
通过表1可得到G中节点连通中心度依次为:
CCON(v1)=0;CCON(v2)=12.1;CCON(v3)=3;
CCON(v4)=9;CCON(v5)=13.47;CCON(v6)=8.33;
CCON(v7)=CCON(v8)=2.07;CCON(v9)=8.67.
可以看出,影响力最大的节点是v5,最小的是v1.
进一步,每个节点的连通中心度与其在网络拓扑结构中的具体位置有着重要的关系.例如,在网络图G中,除节点v1外,v7,v8的连通中心度是最小的,这是因为其余节点之间的经过v7或v8的互不相交的路以及最短路都很少.从而说明在进行信息传播时,节点v7或v8起到的作用很小,对整个网络中的影响也就很小.另外,节点v4的度数小于v9的度数,但v4的连通中心度大于v9的连通中心度.这说明节点的连通中心度不依赖于其度数的大小.
表1 图1所示网络中任意节点对的局部连通度、最短路条数和最小节点割集的并集的计算
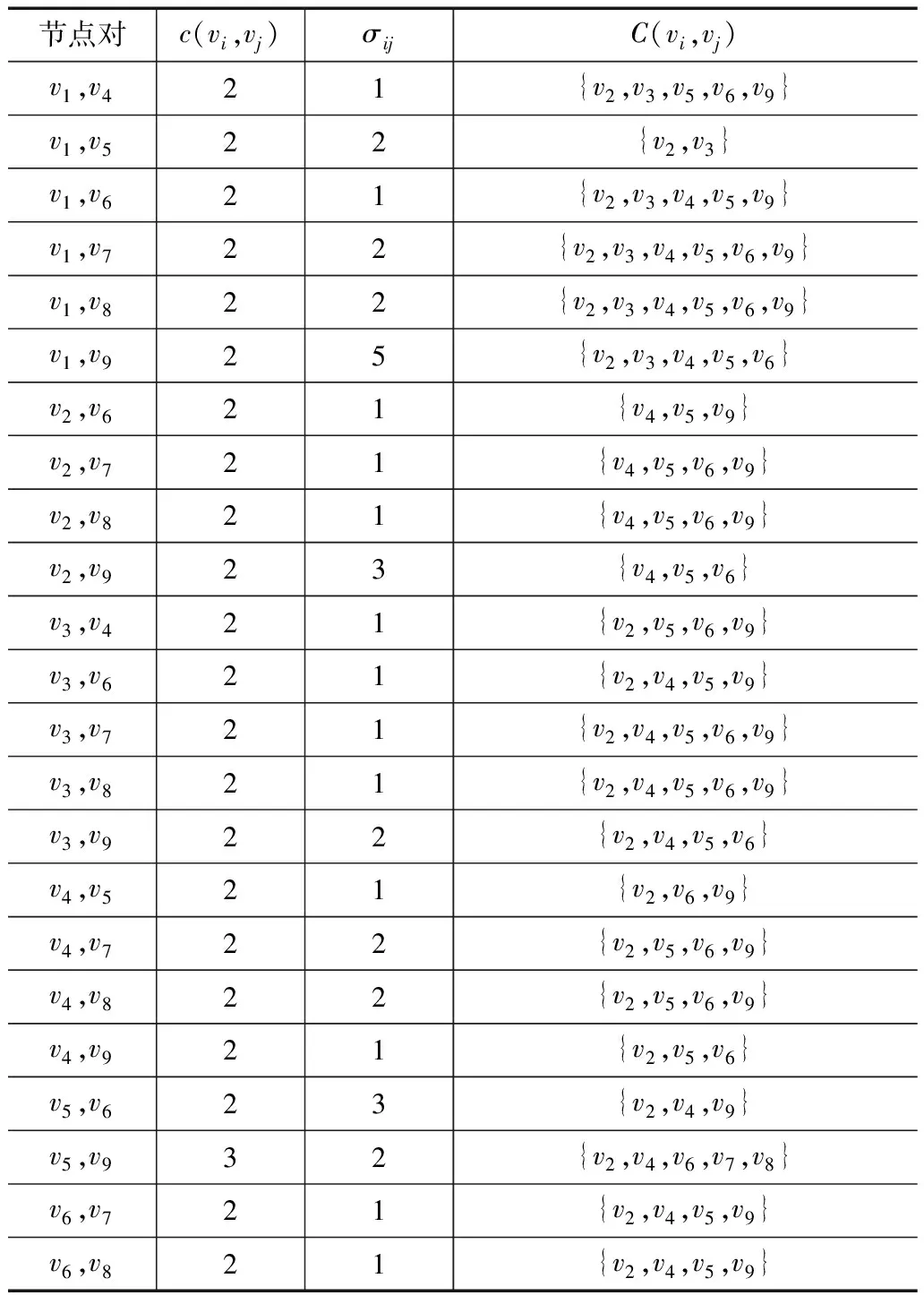
节点对c(vi,vj)σijC(vi,vj)v1,v421{v2,v3,v5,v6,v9}v1,v522{v2,v3}v1,v621{v2,v3,v4,v5,v9}v1,v722{v2,v3,v4,v5,v6,v9}v1,v822{v2,v3,v4,v5,v6,v9}v1,v925{v2,v3,v4,v5,v6}v2,v621{v4,v5,v9}v2,v721{v4,v5,v6,v9}v2,v821{v4,v5,v6,v9}v2,v923{v4,v5,v6}v3,v421{v2,v5,v6,v9}v3,v621{v2,v4,v5,v9}v3,v721{v2,v4,v5,v6,v9}v3,v821{v2,v4,v5,v6,v9}v3,v922{v2,v4,v5,v6}v4,v521{v2,v6,v9}v4,v722{v2,v5,v6,v9}v4,v822{v2,v5,v6,v9}v4,v921{v2,v5,v6}v5,v623{v2,v4,v9}v5,v932{v2,v4,v6,v7,v8}v6,v721{v2,v4,v5,v9}v6,v821{v2,v4,v5,v9}
3 特殊网络中节点的连通中心度
树状网络是最简单的一种连通网络,下面通过一种简单的方法,给出树中任意非叶子节点的连通中心度.
定理2 设T=(V,E)是树,v∈V是T的非叶子节点,则v的连通中心度为
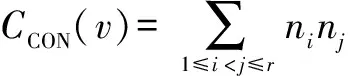
其中r表示T-v的连通分支数,nk表示T-v中第k个连通分支的节点数,k=1,2,…,r.
证明 由于T是树,对T中任意一对不相邻的节点vi,vj,存在唯一的一条路连接节点vi与vj,因此有
所以,节点v只对T-v中不连通分支上的节点对有影响,从而
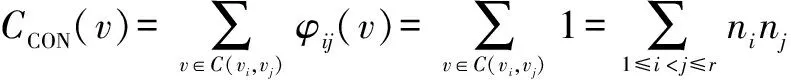
证毕.
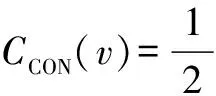
定理3 设C=(V,E)是包含n个节点的圈,n≥5,则C中任意节点v的连通中心度为
证明 对C中任意节点v,C-v中不相邻的节点对的数目为
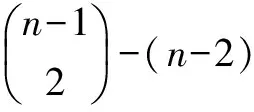
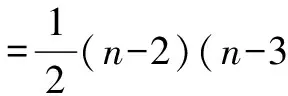
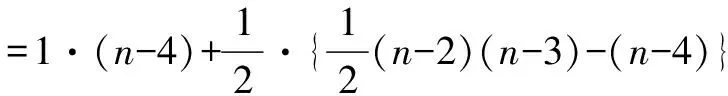
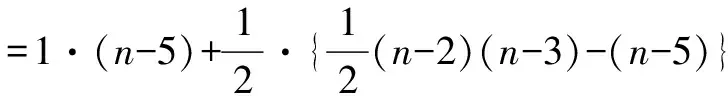
证毕.
定理4 对完全二部图Ks,t,s,t≥2,令Ks,t的二部划分为V1,V2,其中V1={vi:0≤i≤s-1},V2= {uj:0≤j≤t-1},有
(1) 若s≠t,则任意节点vi的连通中心度为
任意节点uj的连通中心度为

其中i=0,1,…,s-1;j=0,1,…,t-1.
(2) 若s=t,则Ks,t中任意节点v的连通中心度为
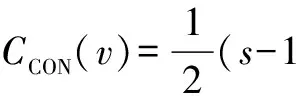
证明
(1) 因为V1,V2是Ks,t的二部划分,所以V1中的节点互不相邻,V2中的节点也互不相邻.故对V1中任意不相邻节点对vi 1,vi2,它们之间存在|V2|条最短路,且对每个V2中的节点uj,有一条最短路经过uj,因此,
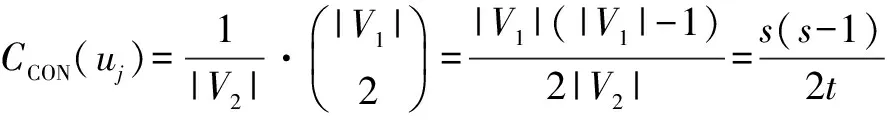
其中j=0,1,…,t-1.
同理可得:
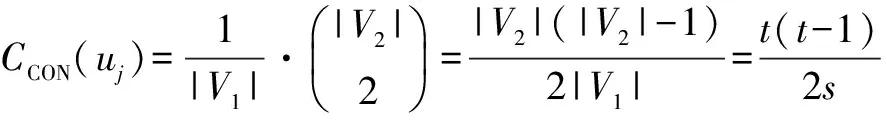
其中i=0,1,…,s-1.
(2) 若s=t,则由上述分析可知,对Ks,t中任意节点v,有
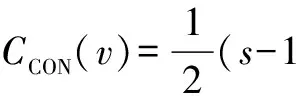
证毕.
定理5 对完全k-部图Kn1,n2,…,nk,令它的k-部划分为V1,V2,…,Vk,则对任意的节点vi∈Vi,vi的连通中心度为
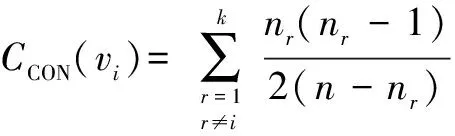
其中i=1,2,…,k,n1+n2+…+nk=n.
证明 由于Kn1,n2,…,nk的不同部分之间的节点都是相邻的,故每对不相邻的节点属于同一部分.对任意的节点对vr1,vr2∈Vr,vr1,vr2之间内部不相交的路的条数为n-nr,因此Vi中的任意节点vi对vr1,vr2的影响力为:
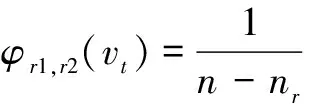
其中i∈{1,2,…,k},且i≠r.进一步,Vr中互不相邻的节点对的数目为:
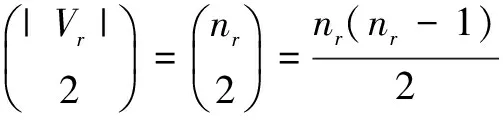
因此,节点vi对Vr中所有节点对的影响了之和为:
所以,节点vi的连通中心度为:
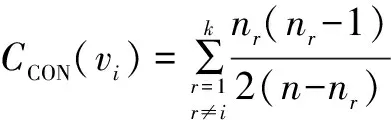
证毕.
4 数据分析
本节以Karate俱乐部成员网络[37]为例,如图2所示,通过连通中心度计算每个成员的影响力,并将此指标与度中心度、紧密中心度和介数中心度等指标进行了比较,其中节点的标号与文献[37]中是一致的.
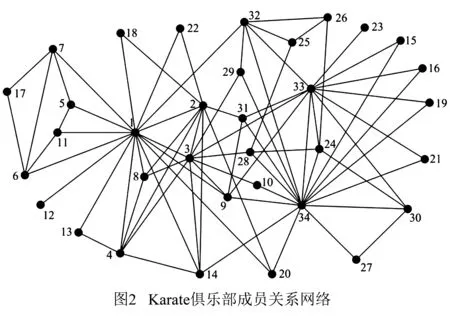
表2 Karate俱乐部网络节点影响力4种度量参数的比较

节点vCDEG(v)CCLO(v)CBET(v)CCON(v)1160.01724231.08235.83290.0147128.4547.993100.0169580.4088.91460.014086.3216.27530.011490.330.33640.0116315.8316.33740.0116315.8316.33840.0133300950.0156329.9631.281020.012990.450.451130.011490.330.331210.01111001320.01124001450.0153821.9628.531520.01124001620.01124001720.00862001820.01136001920.01124002030.0149315.5017.262120.01124002220.01136002310.01042002450.011909.6313.652530.011361.175.172630.011362.038.162720.01087002840.0137011.4615.702930.013510.956.213040.011632.0414.463140.013897.788.233260.0164074.1083.3633120.0156396.18117.3834160.01639145.23155.71
从表2可以看出,通过连通中心度来判断Karate俱乐部网络中各节点的影响力时,影响力最大的5个节点依次为:节点1,节点34,节点33,节点3,节点32.因此,通过连通中心度能够准确地选择影响力较大的节点.
连通中心度与介数中心度比较相似,介数中心度为0的节点的连通中心度也为0,但是,介数中心度不为0的节点,其连通中心度总是大于等于介数中心度,这是因为连通中心度在计算的过程中考虑了每对不相邻节点间的内部互不相交的路的条数,即节点对的局部连通度.
一个节点v的连通中心度表示的是v对其他节点影响的大小,其值与度中心度、紧密中心度以及介数中心度没有必然的联系.例如,对节点30与节点31,CDEG(30)=CDEG(31),CCLO(30)
节点对之间的内部互不相交的路是信息并行传递的基础,因此,利用连通中心度能更好地度量社交网络中节点的影响力.
5 结论
本文在目前两类度量网络节点影响力方法的基础上,即结合了中心度方法和节点删除方法,提出了一种新的刻画网络中节点重要程度的方法.该方法既考虑了节点在网络结构中位置的重要性,也考虑了节点对网络局部连通性的影响,更全面地刻画了节点的重要程度.在信息并行传播的社交网络中,其传播路径为两个节点间的内部互不相交的路,因此对具有这种特征的网络,利用连通中心度来度量节点的重要性更准确一些.
不同性质的网络具有不同的结构特征,我们所考虑的只是无向的连通网络,对有向网络和赋值网络还需进一步的研究.另外,针对规模很大的网络,计算其节点的连通中心度将耗费大量的计算资源,精确计算每个节点连通中心度不现实.所以,将连通中心度应用于大规模网络中时,需要对计算过程做进一步的简化,但要求对节点的连通中心度的影响不太大,这也是一个值得研究的问题.
[1]Newman M E.The structure and function of complex networks[J].SIAM Review,2003,45(2):167-256.
[2]Boccaletti S,Latora V,Moreno Y,et al.Complex networks:Structure and dynamics[J].Physics Reports,2006,424 (4):175-308.
[3]Zhang J,Zhou C,Xu X,et al.Mapping from structure to dynamics:A unified view of dynamical processes on networks[J].Physical Review E,2010,82 (2):026116.
[4]Zhou T,Wang B H.Catastrophes in scale-free networks[J].Chinese Physics Letters,2005,22 (5):1072-1075.
[5]Pastor-Satorras R,Vespignani A.Immunization of complex networks[J].Physical Review E,2002,65 (3):036104.
[6]Freeman L C.Centrality in social networks conceptual clarification[J].Social Networks,1979,1(3):215-239.
[7]Sabidussi G.The centrality index of a graph[J].Psychometrika,1966,31(4):581-603.
[8]Freeman L C.A set of measures of centrality based on betweenness[J].Sociometry,1977,40(1):35-41.
[9]Bonacich P.Factor and weighting approaches to status scores and clique identification[J].Journal of Mathematical Socilogy,1972,2(1):113-120.
[10]Bonacich P.Some unique properties of eigenvector centrality[J].Social Networks,2007,29(4):555-564.
[11]Borgatti S P,Everett M G.A graph-theoretic perspective on centrality[J].Social Networks,2006,28(4):466-484.
[12]Chen D B,Lü L Y,Shang M S,et al.Identifying influential nodes in complex networks[J].Physica A,2012,391 (4):1777-1787.
[13]Chvátal V.Tough graphs and Hamiltonian circuits[J].Discrete Mathematics,1973,5 (3):215-228.
[14]许进,席酉民,汪应洛.系统的核与核度(I)[J].系统科学与数学,1993,13(2):102-110. Xu J,Xi Y M,Wang Y L.On system core and coritivity (1)[J].Journal of System Science and Mathematical Science,1993,13(2):102-110.(in Chinese)
[15]Jung H A.On a class of posets and the corresponding comparability graphs[J].Journal of Combinatorial Theory Series B,1978,24(2):125-133.
[16]Sun J,Tang J.A survey of models and algorithms for social influence analysis[A].Social Network Data Analytics[C].New York:Springer,2011.177-214.
[17]吴信东,李毅,李磊.在线社交网络影响力分析[J].计算机学报,2014,37(4):735-752. Wu X D,Li Y,Li L.Influence analysis of online social networks[J].Chinese Journal of Computers,2014,37(4):735-752.(in Chinese)
[18]Ma S J,Ren Z M,Ye C M,et al.Node influence identification via resource allocation dynamics[J].International Journal of Modern Physics C,2014,25(11):1450065.
[19]Saito K,Kimura M,Ohara K,et al.Super mediator—A new centrality measure of node importance for information diffusion over social network[J].Information Sciences,2016,329:985-1000.
[20]Hu F,Liu Y H.Multi-index algorithm of identifying important nodes in complex networks based on linear discriminant analysis[J].Modern Physics Letters B,2015,29(03):1450268.
[21]Kim H,Anderson R.Temporal node centrality in complex networks[J].Physical Review E,2012,85(2):605-624.
[22]Kas M,Wachs M,Carley K M,et al.Incremental algorithm for updating betweenness centrality in dynamically growing networks[A].Advances in Social Networks Analysis and Mining (ASONAM),2013 IEEE/ACM International Conference on IEEE[C].Niagara Falls,Canada:IEEE/ACM,2013.33-40.
[23]Gao Z X,Shi Y,Chen S Z.Measures of node centrality in mobile social networks[J].International Journal of Modern Physics C,2015,26(09):1550107.
[24]Zhang X,Zhu J,Wang Q,et al.Identifying influential nodes in complex networks with community structure[J].Knowledge-Based Systems,2013,42(2):74-84.
[25]Shakarian P,Salmento J,Pulleyblank W,et al.Reducing gang violence through network influence based targeting of social programs[A].Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining[C].New York,USA:ACM,2014.1829-1836.
[26]He X,Kempe D.Stability of influence maximization[A].Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining[C]. New York,USA:ACM,2014.1256-1265.
[27]Zhou C,Zhang P,Zang W,et al.Maximizing the long-term integral influence in social networks under the voter model[A].Proceedings of the 23rd International Conference on World Wide Web Conferences Steering Committee[C].Seoul,Korea:ACM,2014.423-424.
[28]Morone F,Makse H A.Influence maximization in complex networks through optimal percolation[J].Nature,2015,524(7563):65-68.
[29]Lamba H,Narayanam R.A model-independent approach for efficient influence maximization in social networks[J].Social Network Analysis & Mining,2015,5(1):1-11.
[30]Menger K.Zur allgemeinen Kurventheorie[J].Fundamenta Mathematicae,1927,10:96-115.
[31]Ford L P,Fulkerson D R.Maximal flow through a network[J].Canadian Journal of Mathematics,1956,8(3):399-404.
[32]Ford L P,Fulkerson D R.Flows in Networks[M].Princeton NJ:Princeton University Press,1962.
[33]Edmonds J,Karp R M.Theoretical improvements in algorithmic efficiency for network flow problems[J].Journal of the ACM,1972,19(2):248-264.
[34]Goldberg V A,Tarjan E R.A new approach to the maximum flow problem[J].Journal of the ACM,1988,35(4):921-940.
[35]Floyd R W.Algorithm 97:Shortest path[J].Communications of the ACM,1962,5(6):345.
[36]Johnson D B.Efficient algorithms for shortest paths in sparse networks[J].Journal of the ACM,1977,24(1):1-13.
[37]Zachary W W.An information flow model for conflict and fission in small groups[J].Journal of Anthropological Research,1977,33(4):452-473.

李泽鹏(通讯作者) 男,1987年出生于甘肃定西.北京大学信息科学技术学院博士后,主要研究方向为图论与组合优化,社交网络拓扑结构.
E-mail:lizepeng@pku.edu.cn

左 杨 男,1990年出生于安徽安庆.北京大学信息科学技术学院硕士研究生,主要研究方向为社交网络结构分析.
王宏宇 女,1988年出生于黑龙江牡丹江.北京大学信息科学技术学院博士研究生,主要研究方向为图论与组合优化,社交网络结构.
An Influence Measure of Nodes Based on Structures of Social Networks
LI Ze-peng1,2,ZUO Yang1,2,WANG Hong-yu1,2
(KeyLaboratoryofHighConfidenceSoftwareTechnologies(PekingUniversity),MinistryofEducation,Beijing100871,China; 2.SchoolofElectronicsEngineeringandComputerScience,PekingUniversity,Beijing100871,China)
Identifying the influence of nodes is one of the major research topics in the structural analysis of social networks.The current measures of researching the node influence can be divided into two categories:centrality measure and node removal measure.The former mainly identifies the influence of the node by degree or shortest path,without considering the connectivity of social networks; while the latter by the damage of the structure of a social network when some nodes are removed.The node removal measure is incapable to be applied in large-scale since the computational complexity.We propose a new parameter,connectedness centrality,to identify the influence of nodes in networks by combining the local connectivity and shortest paths.We give a method to compute the connectedness centrality of the node and obtain the precise values in some specific networks.Finally,an experiment using a real-word network shows that our method can well identify the influence of the node in social networks.
social networks; node influence; centrality measure; connectedness centrality; shortest path
2015-01-30;
2016-01-20; 责任编辑:梅志强
国家自然科学基金(No.61672050,No.61372191,No.61572492,No.61572046,No.61502012);国家973重点基础研究发展计划(No.2013CB329600);中国博士后科学基金(No.2016M591013);江西省教育厅项目(No.GJJ150686)
TP399
A
0372-2112 (2016)12-2967-08
��学报URL:http://www.ejournal.org.cn
10.3969/j.issn.0372-2112.2016.12.022

