中国省级碳生产率及其收敛性分析

蒋雨桥，周大川

（中南财经政法大学经济学院，湖北武汉 430073）

中国省级碳生产率及其收敛性分析

蒋雨桥，周大川

（中南财经政法大学经济学院，湖北武汉 430073）

减少碳排放、保持经济增长的唯一出路在于提高碳生产率。目前我国各省平均碳生产率呈东部、中部、西部递减的态势，但整体上来讲我国的碳生产率呈增长趋势；碳生产率变化随技术变化的波动而波动；我国碳生产率的离散程度随着时间推移逐年递减，全国各地区的碳生产率水平差异在逐年减小。为提高我国各地区碳生产率，达到节能减排的目的，政府应该因地制宜，根据各地区的不同特点制定相应的政策，并加强各区域间的技术交流合作，缩小地区间的碳生产率差异，全面提升我国碳生产率。

碳生产率；收敛；全域生产率指数

一、导言

全球经济飞速发展所产生的气候变化是当前各国关注的热点问题，导致全球气候变化的主要原因是温室气体的排放。而温室气体排放的增多会对人类社会造成全球性和长期性的影响，各国对以二氧化碳为代表的温室气体的减排问题日益重视。联合国气候变化专门委员会（IPCC）于1992年通过的《联合国气候变化框架公约》为世界各国如何解决全球气候变化问题指明了道路。

改革开放以来，我国经济以10%左右的经济增长率持续增长了30多年。虽然经济发展迅速，但能源也在过度使用。我国十分重视温室气体的节能减排并大力发展低碳经济。减少碳排放、保持经济增长的唯一出路在于提高碳生产率（Beinhocker et al.，2008）。中国各省份的碳生产率是如何变化的？它们是呈收敛还是发散趋势？本文试图对这些问题进行研究。

二、各省市碳生产率的计算

（一）碳排放量的计算。

本文借鉴潘家华（2011）的计算方法，[1]根据《2006年IPCC国家温室气体清单指南》提供的估算化石燃料燃烧二氧化碳排放量方法进行计算。二氧化碳排放总量通过先求出各种能源消费产生的二氧化碳排放估计量再将其求和得到，具体计算公式如下：

上式中，化石燃料主要选取《中国能源统计年鉴》所统计的原煤、焦炭、原油、汽油、柴油、燃料油、天然气以及煤油等八种。CEFi和COFi分别为IPCC（2006）提供的各类化石燃料的含碳量与各类化石燃料的碳氧化因子；NCVi、CEFi和COFi的乘积即为各类化石燃料的碳排放系数；12和44分别为碳和二氧化碳的化学分子量，各类化石燃料的碳排放系数如表1所示。

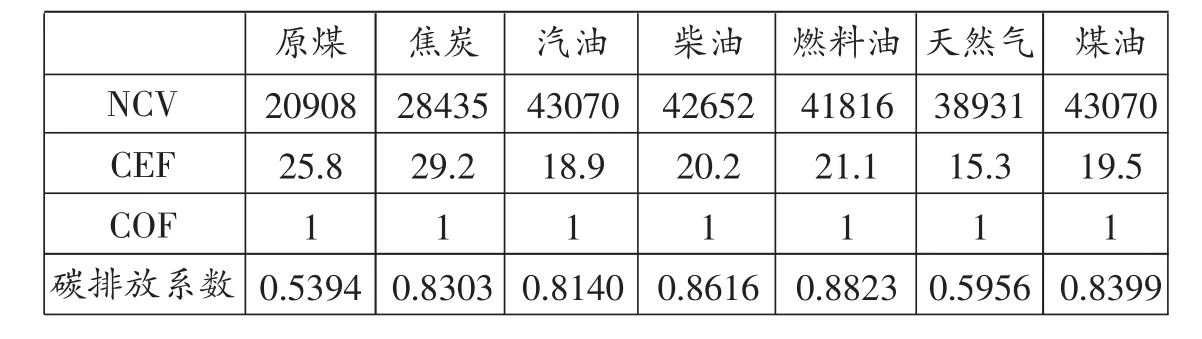
表1 各类化石燃料的碳排放系数①NCV单位为kJ/kg（天然气除外，为kJ/m3），CEF单位为kgC/GJ，天然气碳排放系数单位为kgC/m3，其他燃料的碳排放系数单位为tC/t。需要说明的是，由于笔者收集的天然气消耗量的原始数据以m3为单位，所以测算的天然气的碳排放系数为0.5956kgC/m3而非潘家华和张丽峰（2011）等文献中的0.4478tC/t。

本文计算了1998—2013年全国30个省市的二氧化碳排放量（除港澳台地区外，由于西藏数据严重缺乏，不利于后续计量分析，故剔除）。历年各省市八种化石燃料消耗数据来源于《中国能源统计年鉴》，由于部分省份少数年份能源消耗数据缺乏，本文对其采用一定方法估算。②2001年和2002年宁夏、2002年海南8种化石燃料消耗数据缺失，因此本文估算了这3个数据。具体方法为：2002年宁夏和2002年海南能源消耗总量（以万吨标准煤计）数据可在《中国能源统计年鉴》中获得，本文将其转化为原煤数据后再与原煤碳排放系数相乘得到2002年的二氧化碳排放数据。2001年宁夏二氧化碳排放量则采用2000年和2002年的算数平均值。

（二）碳生产率的计算。

本文将采用SBM方向性距离函数和GML指数，对1998—2013年我国30个省市的碳生产率进行测算。以下将对模型进行说明。

1.全域生产可能性集。

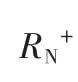
生产可能性集满足如下假设：（1）闭集和有界集；（2）“好”产出具有强可处置性，投入有自由可处置性；（3）产出具有联合弱可处置性；（4）零结合公理，即没有“坏”产出就没有“好”产出。运用DEA方法可以将当期的生产可能性集表示如下：

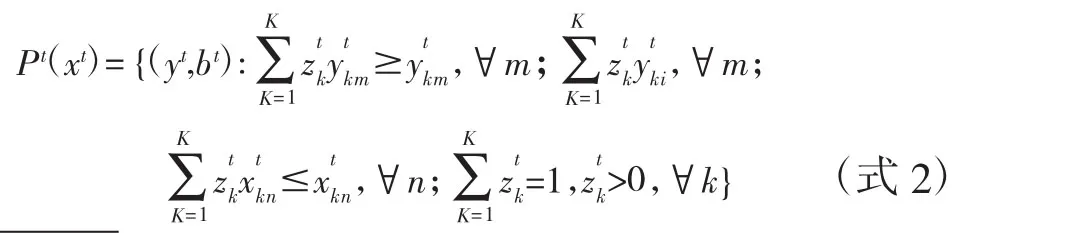
式中，Ztk为每个横截面观察值的权重。GML指数需要将当期生产可能性集Pt（xt）替换为全域生产可能性集PG（x），P1（x1）=P1（x1）∪P2（x2）∪…∪PT（xT）运用DEA方法可表示为：

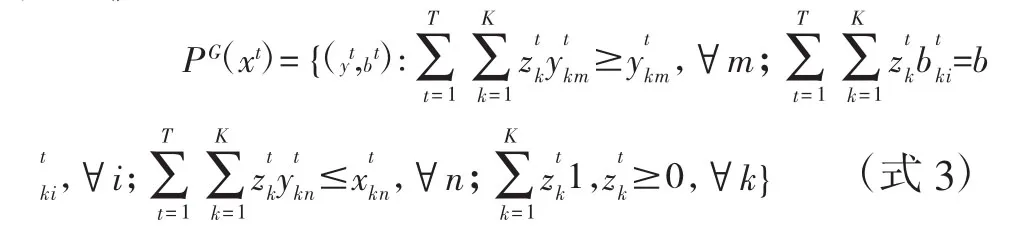
2.全域SBM方向性距离函数。

借鉴Fukuyama and Weber（2009）的方法，[3]本文将考虑二氧化碳排放的全域SBM方向性距离函数定义为：

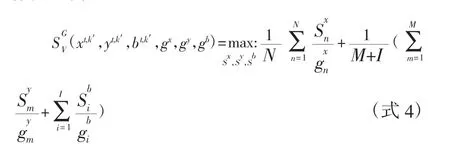
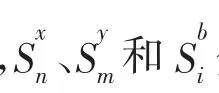
3.GML指数。

本文引入GML指数来测度我国30个省市历年的碳生产率。参照Oh（2010）的方法，[4]将GML指数建立在全域SBM方向性距离函数的基础上，它可以表示为：

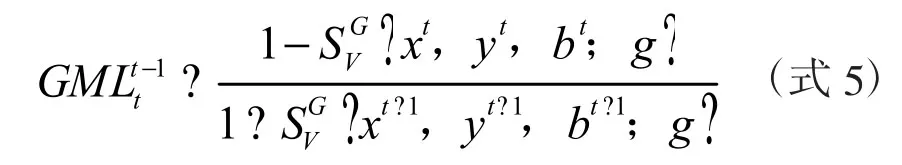
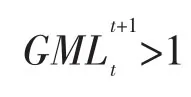
表示从t到t+1时期效率提高（降低）和技术进步（退步）。

（三）数据来源。

本文选取了中国30个省市1998—2013年的“好”产出、“坏”产出以及劳动、资本和能源投入的基础数据。各变量的定义如下：

（1）“好”产出。即选用各省市以1998年为基期的实际地区生产总值（GRP），数据来源于历年的《中国统计年鉴》。

（2）“坏”产出。即采用各省市历年二氧化碳排放数据，原始数据来源于历年《中国能源统计年鉴》。

（3）劳动投入。即选取各省市单年平均从业人员人数作为投入变量。从业人员是指16周岁及以上，从事一定社会劳动并取得劳动报酬或经营收入的人员，这一指标反映了一定时期内全部劳动力资源的实际利用情况。该指标采用当年年初与年末的算数平均数。原始数据来源于历年各省市统计年鉴。

（4）资本投入。估算按可比价格计算的资本存量最常用的方法是“永续盘存法”，该法可表示为其中，t指第t年，i指第i个省（市）。该式需确定四个变量，分别是基年资本存量K，当年投资I，投资品价格指数和折旧率δ。本文采取张军等（2004）的做法，[5](p35-44)选取以1952年不变价计算的1998年的物质资本存量作为基年资本存量；①张军将重庆的数据并入四川，而本文以1998年四川和重庆的名义GDP为权重将资本存量拆分得到四川和重庆的基年资本存量数据。固定资本形成总额作为当年投资I，该数据来源于《中国统计年鉴》；固定资产投资价格指数作为投资品价格指数，该数据来源于《中国统计年鉴》；折旧率选取张军估计的各省市固定资本形成总额的经济折旧率9.6%。由此得到各省市以1998年为基期的年末资本存量。

（5）能源投入。选取各省市能源消耗总量（以标准煤计）作为投入变量，数据来源于历年《中国能源统计年鉴》。

根据上述思路，本文计算了我国30个省市的碳生产率，并将其分解为效率变化指数和技术变化指数，以探究碳生产率增长的来源。表3给出了基于GML指数的1998—2013年中国各省市的平均碳生产率以及效率变化指数和技术变化指数。

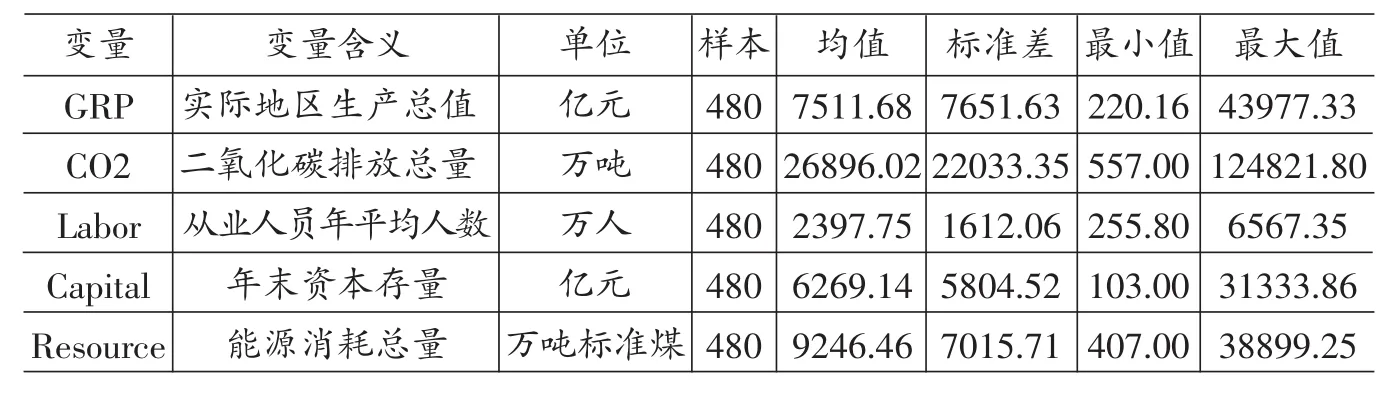
表2 碳生产率测算的投入产出指标的描述性统计情况

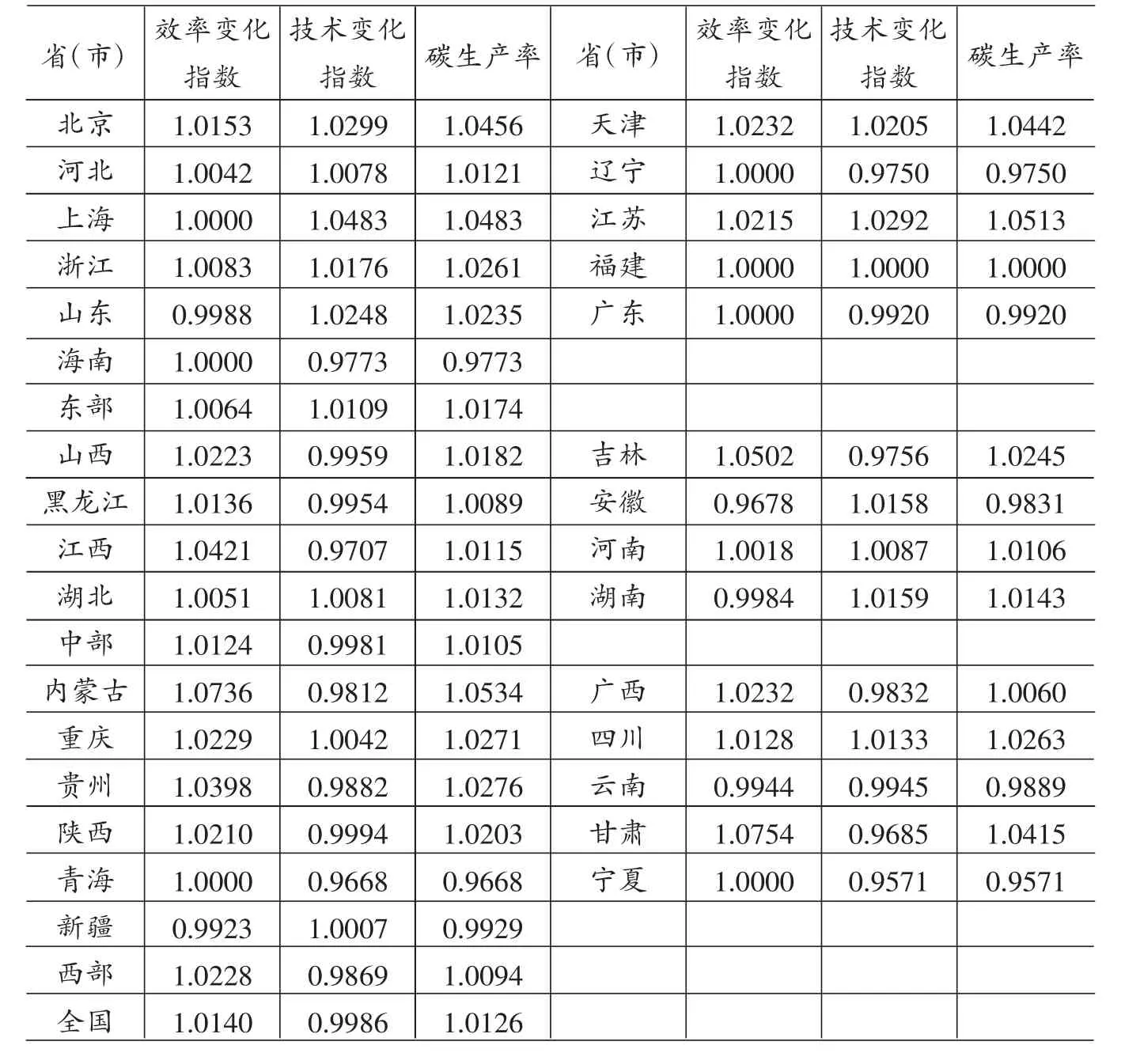
表3 1998-2013年各省市的平均碳生产率①

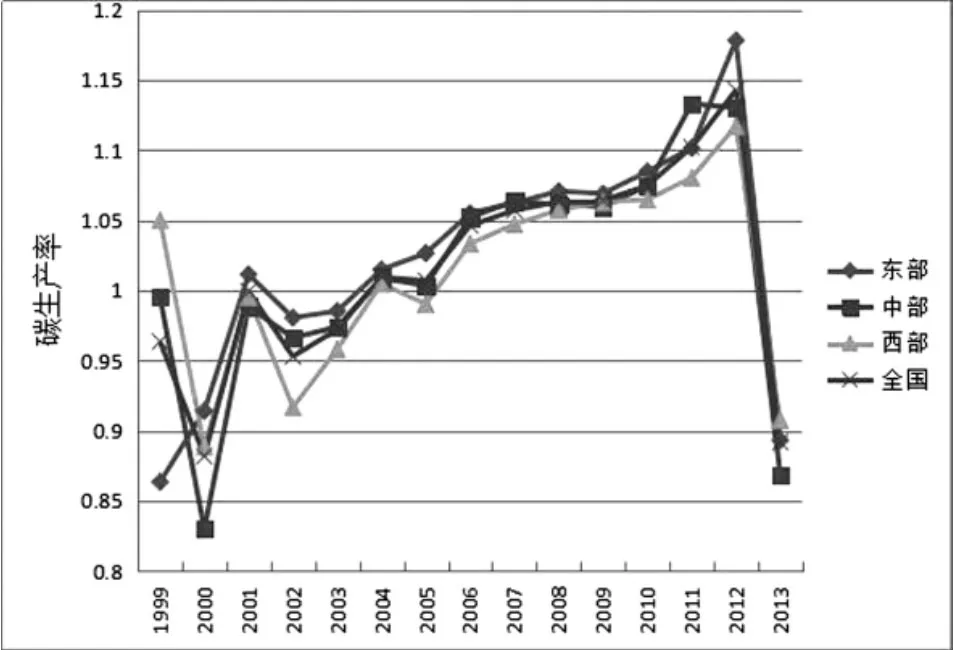
图1 全国及各区域历年碳生产率

由图1可以发现全国、东部、中部和西部碳生产率的变动趋势大致相同，基本可以分为三个阶段：（1）1999—2004年，全国和三大区域碳生产率从低于1的水平上升到高于或等于1；（2）2004—2012年，全国和三大区域碳生产率均在高于水平1上增长，且增长趋势几乎一致，这说明从整体上讲全国这段时间碳生产率水平在稳步提升；（3）2012—2013年，全国及三大区域碳生产率从1.15左右突然下降到0.9左右，这说明2013年的二氧化碳排放绩效有明显下降。后文将通过图4分析全国和各地区碳生产率的来源情况。

由图2可知全国、东部、西部和中部碳生产率曲线的波动与技术变化曲线的波动一致。这说明碳生产率变化随技术变化的波动而波动，我国碳生产率变动易受技术变化的影响。

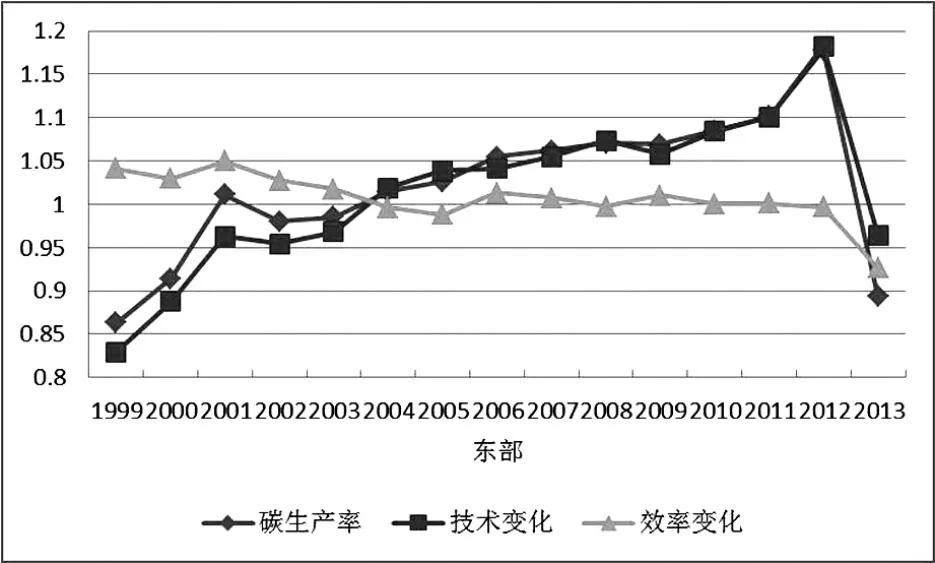
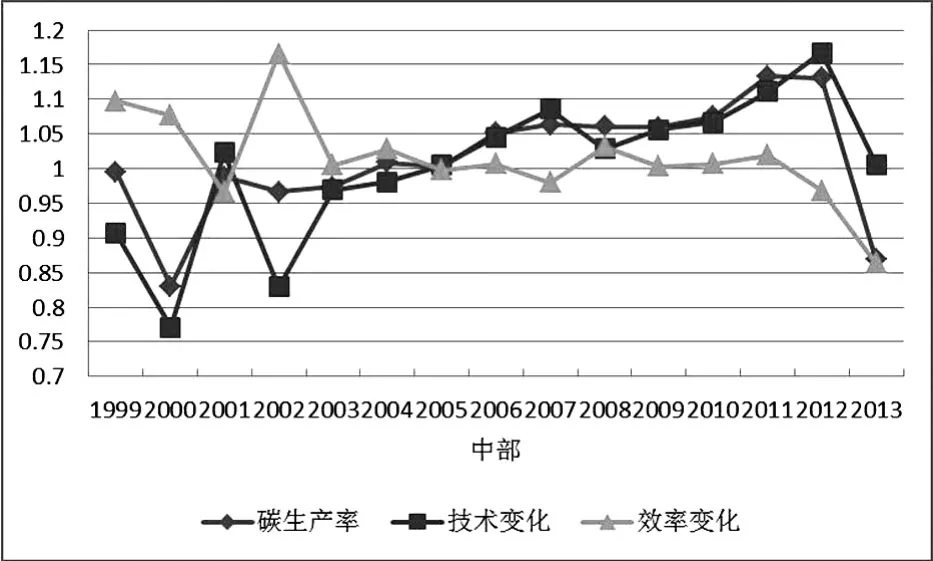
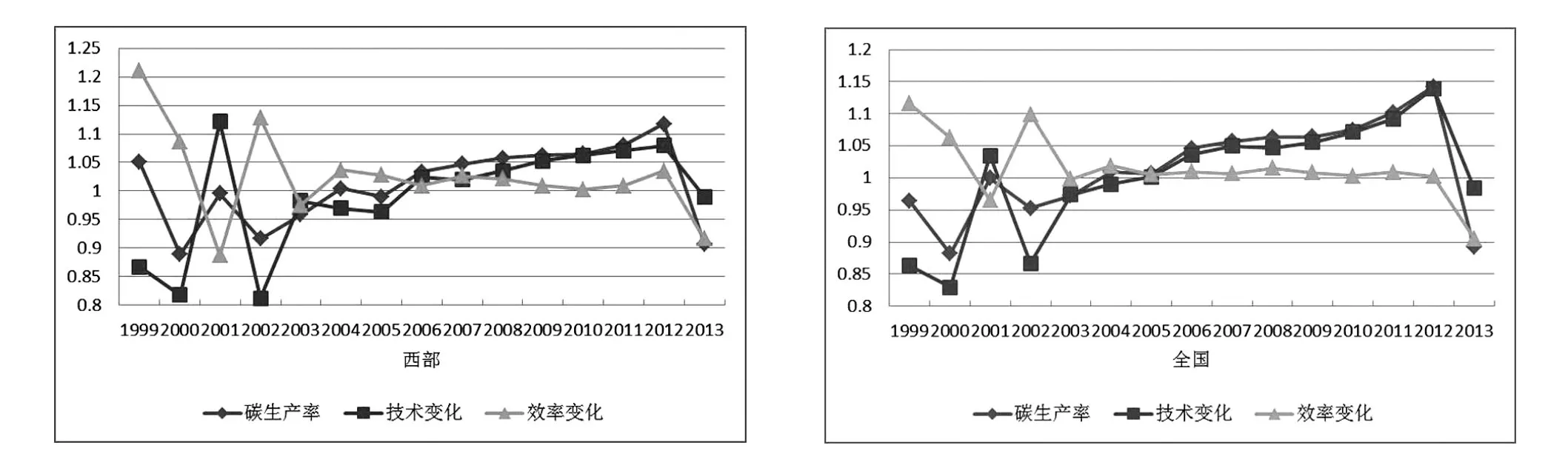
图2 全国和三大区域碳生产率、技术变化和效率变化图

三、各省市碳生产率收敛性分析

本节采用δ收敛进行收敛分析。离散程度是检验δ收敛的重要指标，如果碳生产率的离散程度随时间的推移呈逐渐缩小的趋势，则说明存在δ收敛。本文用标准差、变异系数和δ收敛系数来分析各地区碳生产率的差异。

区域碳生产率标准差是指该区域中各省市碳生产率值与该区域碳生产率算数平均数的离差平方的算数平均数的平方根。标准差是反映数据分布离散程度的测度值之一，它不仅能说明平均碳生产率的代表性，也能说明各省市碳生产率水平值与平均碳生产率的平均变异程度，标准差越大表示离散程度越大。具体计算公式如下：

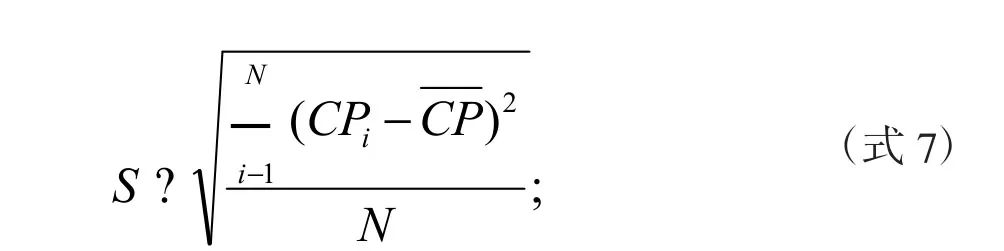
上式中，i为省（市），CPi表示i省（市）的碳生产率，表示区域内碳生产率平均值，N为区域内省市的数量，S表示标准差。

由图3可以发现，全国、东中西部碳生产率标准差都基本呈U型。东部地区的标准差在2009年之前呈递减趋势，2009年之后则呈现递增趋势；全国、中部和西部的标准差在2010年之前呈递减趋势，2010年之后则呈现递增趋势。从标准差的趋势线看，东部地区趋势线几乎水平，说明碳生产率的离散程度基本没有发生变化，δ收敛特征不明显；中部和西部地区趋势线明显向右下方倾斜，说明碳生产率的离散程度有递减趋势，δ收敛特征明显；全国范围内的标准差趋势线也向右下方倾斜，说明全国碳生产的离散程度有递减趋势，存在δ收敛特征。总体来说，通过标准差验证，可以发现我国碳生产率存在δ收敛，碳生产率离散程度随时间推移有缩小的趋势。

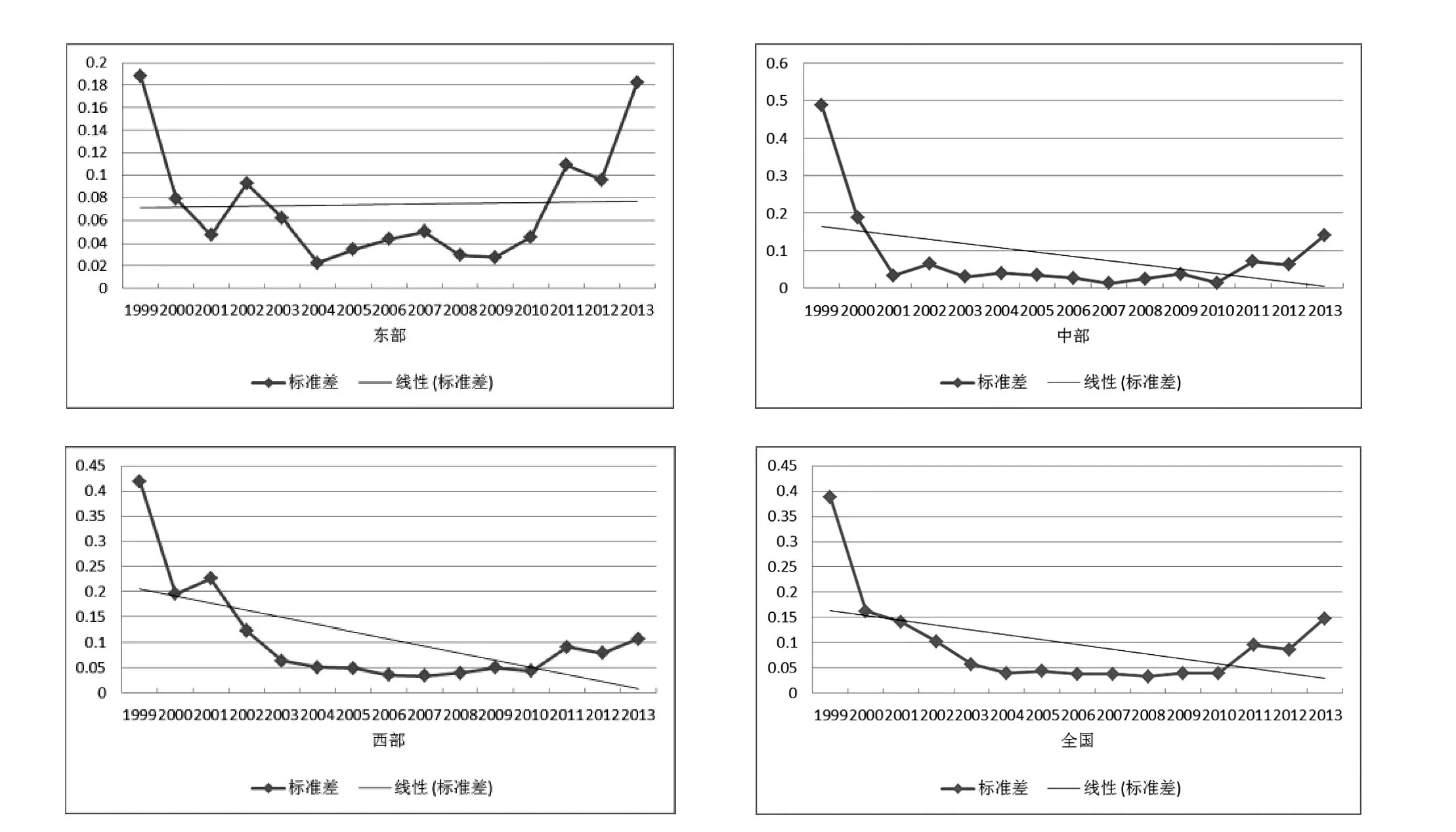
图3 全国及各区域标准差变化趋势

图4 全国及各区域变异系数变化趋势

标准差反映的是离散程度的平均值，而变异系数是标准差与平均值的比值。变异系数是衡量离散程度使用得较多的指标之一，变异系数越大说明该组数据的离散程度越大；变异系数越小说明该组数据的离散程度越小。具体计算公式如下：

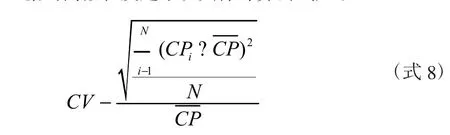
上式中，i为省（市），CPi表示i省（市）的碳生产率，CP表示区域内碳生产率平均值，N为区域内省市的数量，CV表示变异系数。

由图4可知，全国、东部、中部和西部碳生产率变异系数同标准差一样都基本呈U型。U型曲线的拐点同标准差U型曲线一致，东部出现在2009年，全国、中部和西部出现在2010年。从趋势线看，东部的变异系数趋势线出现向右下方倾斜的迹象，这说明从变异系数考虑，东部碳生产率的离散程度有逐年递减的趋势，出现δ收敛的特征。全国、中部和西部碳生产率的离散程度有逐年递减的趋势，存在δ收敛的特征。通过变异系数验证，可以发现我国碳生产率存在δ收敛，碳生产率离散程度随时间推移有缩小的趋势。

为了更好地识别国家间增长收敛或发散的趋势，Barro and Sala-I-Martin（1991、1992、1995）提出了度量收敛的两个指标，其中一个是δ收敛系数。[6](p3-14)δ收敛系数是指样本期每年的所有国家生产率对数的方差，如果该系数逐年递减，则说明这些国家的经济增长存在收敛性。本文使用的δ收敛系数是指每一年各区域中每个省市碳生产率对数的方差，具体公式如下：

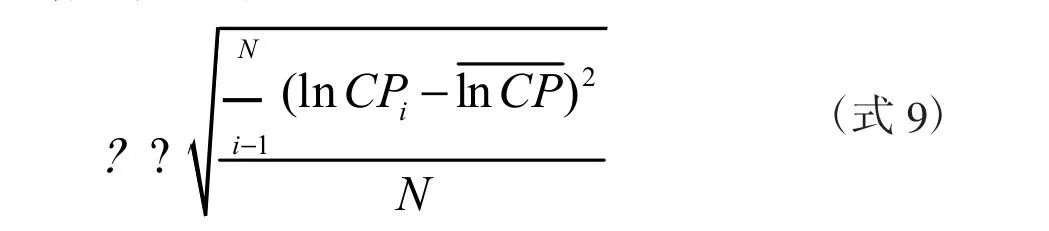
上式中，i为省（市），lnCPi表示i省（市）碳生产率的自然对数，表示区域内碳生产率自然对数的平均值，N为区域内省市的数量，δ为δ收敛系数。

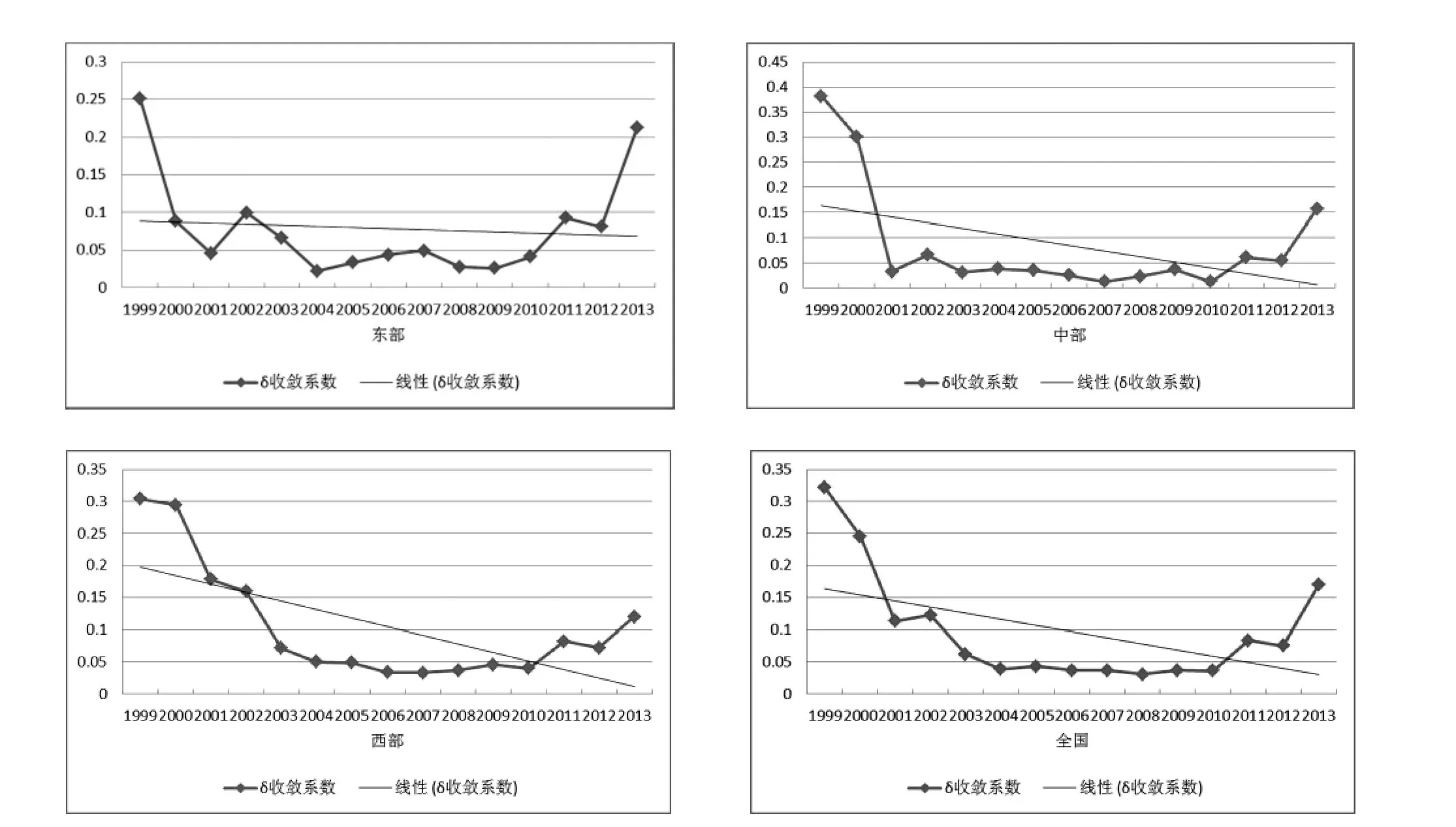
图5 全国及各区域δ收敛系数变化趋势

由图5可以发现，全国及各区域δ收敛系数基本与变异趋势一致。全国、东中西部的δ收敛系数的趋势线均明显地向右下方倾斜，说明它们的碳生产率的离散程度均随时间的推移而递减，存在δ收敛特征。

四、结论

由于我国幅员辽阔，各地区碳生产率特征差异明显。若想提高我国各地区碳生产率，达到节能减排的目的，政府必须因地制宜，充分了解各地区经济发展水平、资源禀赋、产业结构、城市化水平等特点，根据这些特点制定相应的政策。对于碳生产率较低的中西部地区，可以指定更为严格的节能减排目标，并给予政策、资金和技术方面的支持；对于碳生产率较高的东部地区，则可以指定较宽松的减排目标。与此同时，应加强各区域间的技术交流合作，使我国内部也能产生知识溢出效应，缩小我国各地区碳生产率差异，全面提升我国碳生产率。

[1]潘家华，张丽峰.我国碳生产率区域差异性研究[J].中国工业经济，2011，（5）.

[2]Färe，R.，Grosskopf，S.，Pasurka，C.A.，2007，Environmental production functions and environmental directional distance functions[J].Energy，32(7).

[3]Fukuyama，H.，Weber，W.L.，2009，A Directional Slacks-based Measure of Technical Inefficiency[J]，Socio-economic Planning Science，43（4）.

[4]Oh，D.H.，2010，A Global Malmquist-Luenberger Productivity Index[J].Journal of Productivity Analysis，34（2）.

[5]张军,吴桂英,张吉鹏.中国省际物质资本存量估算：1952—2000[J].经济研究，2004，（10）.

[6]林毅夫，刘明兴.中国的经济增长收敛与收入分配[J].世界经济，2003，（8）.

责任编辑 王京

F124.5

A

1003-8477（2016）12-0096-07

蒋雨桥（1997—），男，中南财经政法大学经济学院本科生；周大川（1992—），男，中南财经政法大学经济学院研究生。