电力变压器螺旋式绕组辐向短路合力的计算与分析

李祎春,刘文里,李 军,白仕光

(1.哈尔滨理工大学 电气与电子工程学院,哈尔滨 150080;2.山东海力史必驰自动控制技术有限公司,上海 2018000)



●输变电与特高压●

电力变压器螺旋式绕组辐向短路合力的计算与分析

李祎春1,刘文里1,李 军2,白仕光1

(1.哈尔滨理工大学 电气与电子工程学院,哈尔滨 150080;2.山东海力史必驰自动控制技术有限公司,上海 2018000)

以“场-路耦合”原理为基础,以MagNet有限元软件为平台,针对一台80 000 kVA/110 kV双绕组有载调压电力变压器,分别建立调压绕组不同分接情况下计及绕组不平衡安匝的二维有限元模型。基于考虑铁心材料非线性的影响,采用瞬态非线性求解,对该模型的瞬态漏磁场进行分析,计算出变压器螺旋式绕组的辐向短路力与切向短路力。对二者进行合成得到螺旋式绕组短路工况下的辐向短路合力并对其进行稳定性校核,对螺旋式绕组在切向短路力作用下确保其稳定性的临界压应力进行了推算。结果表明,可应用文中理论与模型对螺旋式绕组辐向短路合力进行计算与稳定性分析。

变压器;螺旋式绕组;不平衡安匝;辐向短路力;切向短路力

目前,变压器失稳事故中主要为低压绕组的辐向失稳。而且大型电力变压器的低压绕组多采用螺旋式结构,然而国内外学者进行螺旋式绕组辐向稳定性分析时均忽略了切向短路力[1]与辐向短路力共同对辐向稳定性的作用,因此准确计算出绕组的实际辐向短路力,对确保变压器的稳定运行具有重要意义。本文以一台80 000 kVA/110 kV双绕组有载调压电力变压器为例,建立变压器绕组安匝分布不平衡的二维有限元模型,并采用瞬态非线性求解,计算出螺旋式绕组各线饼的辐向短路力与切向短路力,并对二者进行合成,以得到变压器短路工况下各线饼的辐向短路合力,为变压器设计及维护人员提供参考。

1 计算原理

1.1 “场-路耦合”法

基于“场-路耦合”原理,以MagNet有限元软件为平台,建立变压器低压绕组出口处发生三相对称短路时,计及绕组安匝不平衡的二维有限元模型。变压器内部采用磁场,外部采用电路参数连接[2],如图1所示。

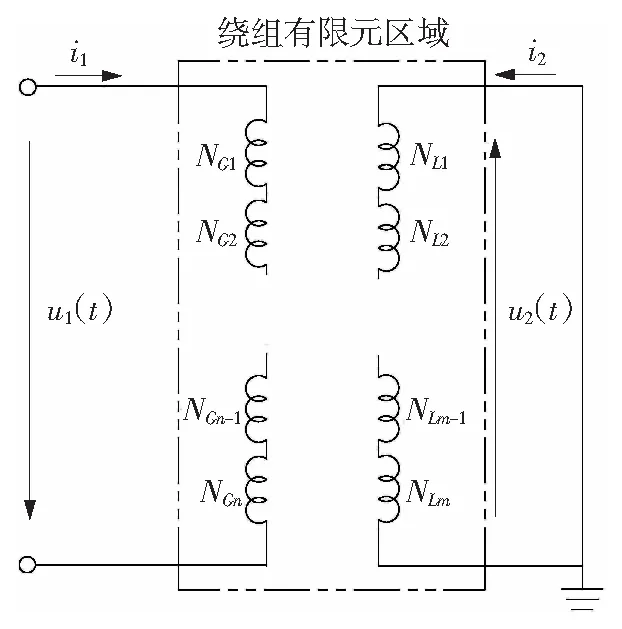
图1 变压器“场-路”耦合分析模型

高压绕组边值问题表达式为

(1)

式中:Ak、Jk、NHk、Kk、Sk、ek、lk、Rkσ、Lkσ分别为高压绕组第k饼上的向量磁位、电密、匝数、占空比、横截面积、感应电势、长度、等效电阻以及等效漏电感;n为高压绕组总线饼数;u1(t)为高压绕组外接电源。

低压绕组边值问题表达式为

(2)

式中:Ai、Ji、NLi、Ki、Si、ei、li、Riσ、Xiσ、Liσ分别为低压绕组第i饼上的向量磁位、电密、匝数、占空比、横截面积、感应电势、长度、等效电阻、等效电抗以及等效漏电感;m为低压绕组总线饼数;Zσ为低压绕组等效漏阻抗;u2(t)为低压绕组端电压。

油区域的表达式为

2A=0

(3)

对式(1)～(3)进行离散处理,得到“场-路”耦合的有限元方程为

式中:A、I、E分别为对应节点的向量磁位矩阵、电流矩阵、电动势矩阵;KAA为向量位刚度矩阵;Kii为电阻刚度矩阵;KAi为电流-磁位耦合刚度矩阵;U0为外加电压矩阵。

1.2 辐向短路合力计算

由于螺旋式绕组在绕制过程中存在一定的螺旋升角,故该绕组中的短路电流可分解为轴向短路电流与辐向短路电流,轴向短路电流与辐向漏磁相互作用产生可使绕组发生扭转变形的切向短路力[3]。螺旋式绕组展开示意图如图2所示。

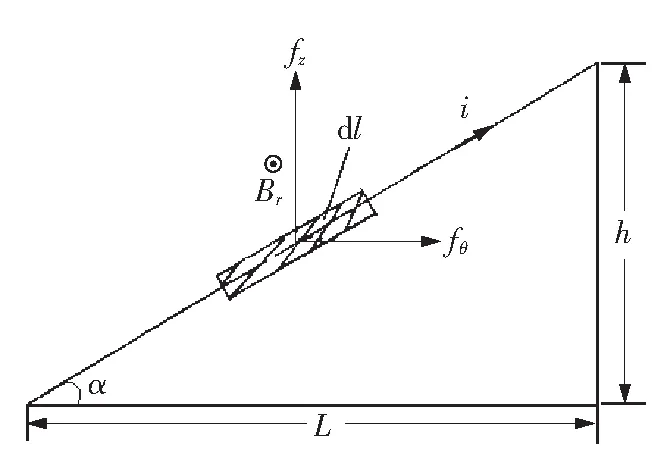
图2 螺旋式绕组展开示意图

由图2可知,螺旋式绕组的螺旋升角为[4]

(4)

螺旋式绕组线饼单位长度切向短路力密度为

fθ=Brisinα

(5)

螺旋式绕组线饼单位长度切向短路力为

(6)式中:r为螺旋绕组内半径,m;h为螺旋式绕组每饼轴向尺寸与相邻油道尺寸之和,m;isinα为绕组线饼中的短路电流轴向分量,A;Br为辐向磁密,T。

螺旋式绕组辐向短路合力求解示意图如图3所示。由图3可知,螺旋式绕组上辐向短路力与切向短路力始终是相互垂直的,故有

(8)

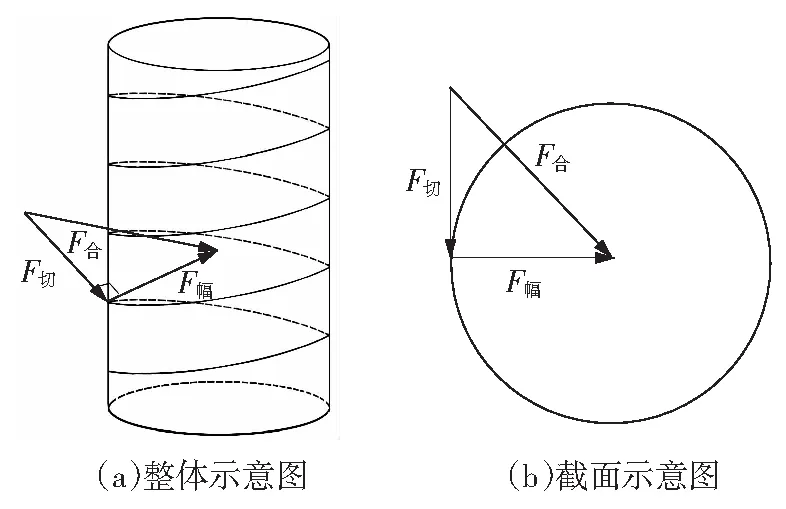
图3 螺旋式绕组辐向短路合力示意图

2 实例计算

基于上述原理,以一台80 000 kVA/110 kV双绕组有载调压电力变压器为例进行计算与分析,变压器主要参数如表1所示,绕组参数如表2所示。

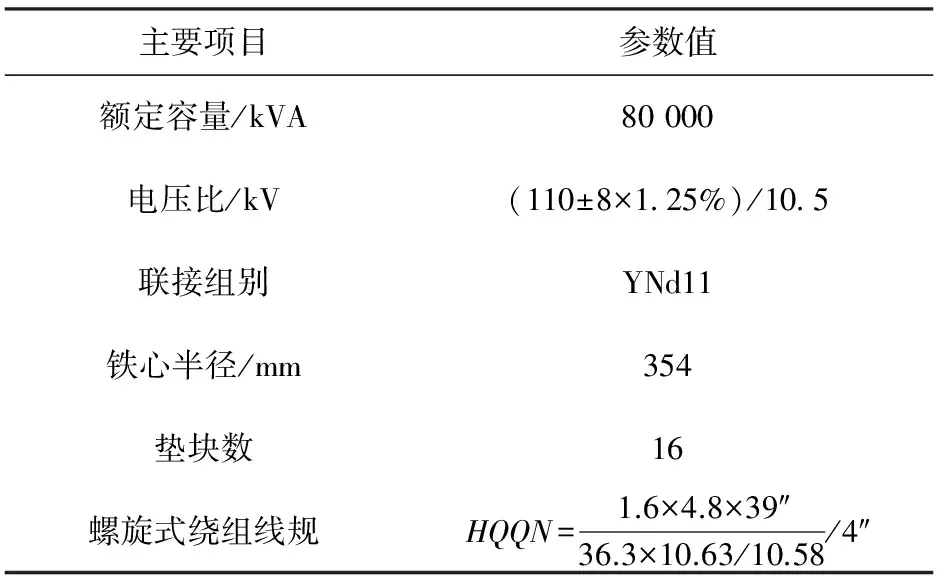
表1 实例变压器主要参数

表2 绕组参数

2.1 模型的建立与验证

对实例变压器的建模与分析做如下假设[5]:

1) 将变压器漏磁场视为二维非线性场。

2) 忽略绕组导线涡流去磁的影响,视金属导体的电导率为常数。

由于变压器低压绕组出口处发生三相对称短路,故只对其中一相以绕组线饼为单位并计及线饼的实际结构、相对位置与铁心实际尺寸进行建模,如图4所示。

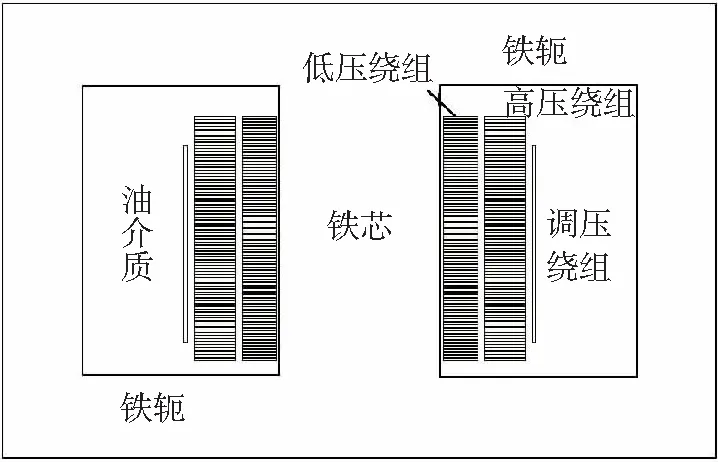
图4 变压器有限元模型

以短路阻抗为标准,应用谐波分析法对所建模型进行校核,数据如表3所示。

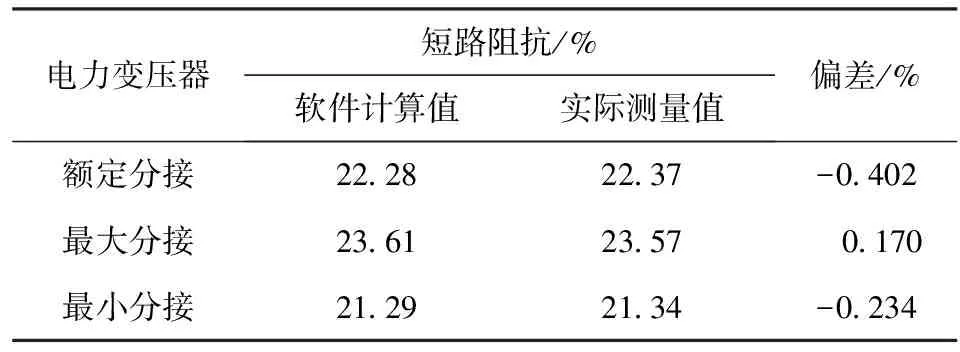
表3 短路阻抗计算值与实测值比较

由表3可知,不同分接情况下的偏差均符合实际工程要求,证明了MagNet所建立的模型可以用于后续的计算与分析。

2.2 短路电流与漏磁场的计算与分析

调压绕组最小分接时短路电流峰值随时间变化情况如图5所示。

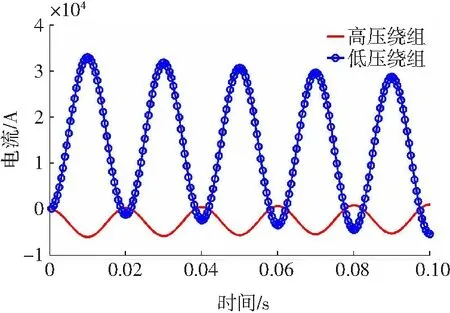
图5 短路电流随时间变化曲线

从图5中可知,短路电流呈非正弦变化,这是因为短路电流是由周期性分量与非周期性分量相互叠加而成的,短路电流的非周期性分量随着时间的延长而逐步衰减直至趋近于零。t=0.01 s时,短路电流峰值最大,此时高、低压绕组短路电流峰值的最大值分别为-5514.842 A和30 023.6 A;高、低压绕组最小分接时短路电流峰值均为正常运行时的11.82倍,这说明所求得的短路电流峰值是正确的[6]。

磁力线分布如图6所示。

图6 磁力线分布图

由图6可知,因主空道处磁势最大,该处磁力线最为稠密,调压绕组的加入使得安匝分布不平衡程度加剧,故最大、最小分接时磁力线的分布与额定分接时差别较大,且最小分接时差别更大。磁力线在绕组端部发生严重弯曲[7],这是因为磁力线在磁阻偏小的铁芯和铁轭中更易闭合,由于所建模型为安匝不平衡模型,因此在高、低压绕组端部以外的位置磁力线亦有弯曲的现象[8]。

t=0.01 s时沿绕组高度方向螺旋式绕组辐向、轴向漏磁变化趋势如图7、图8所示。

图7 低压绕组辐向漏磁分布曲线

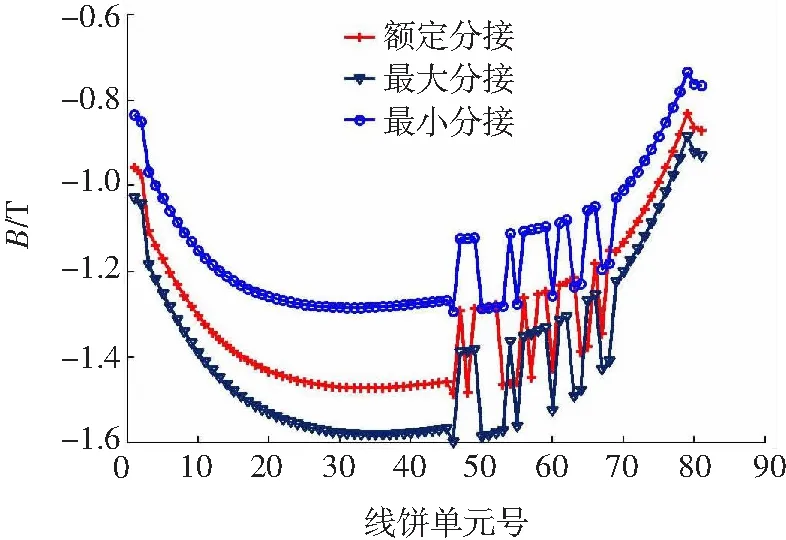
图8 低压绕组轴向漏磁分布曲线

由图7可知,磁力线在绕组端部弯折严重,故端部的辐向漏磁最大,而中部磁力线几乎平行于绕组,因此辐向分量近似为零。调压绕组的接入对低压绕组的辐向漏磁影响并不大。由图8可以看出,低压绕组上半部轴向漏磁分布不均匀,这是由于低压螺旋式绕组绕制过程中采用不等距换位,使得换位处油道间隙大于其他部位所致,而且上端部的轴向漏磁略大于下端部,其缘于绕组上端部距离铁轭比下端部要远,使得磁力线弯曲更为明显。

2.3 辐向短路合力的计算与分析

由以上分析可以知,低压绕组端部的磁力线向左弯曲,短路电流由低压绕组上端部流出,且螺旋式绕组为右绕向,根据左手定则可知切向短路力的方向始终与绕组相切,并且为向内绷紧力。

t=0.01 s时螺旋式绕组沿高度方向的切向短路力变化趋势如图9所示。

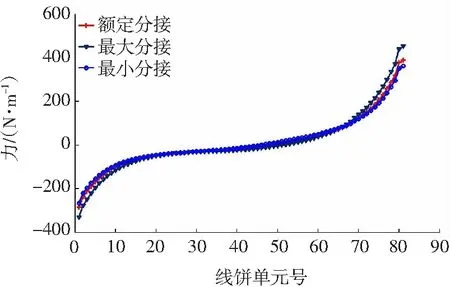
图9 低压绕组切向短路力分布曲线

低压绕组切向短路力的最大值出现在调压绕组最大分接时的第81号线饼处,为509.35 N/m。不同分接情况下第81号线饼上切向短路力随时间变化情况如图10所示。

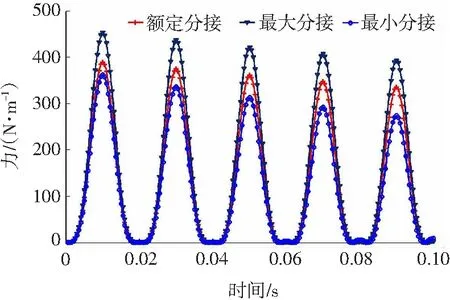
图10 低压绕组切向短路力随时间变化曲线

t=0.01 s时螺旋式绕组沿高度方向辐向短路力变化趋势如图11所示。

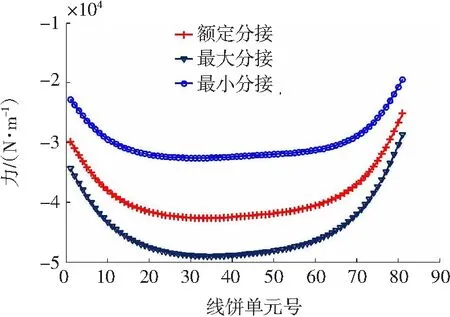
图11 低压绕组辐向短路力分布曲线

从图11可知,低压绕组辐向短路力最大值出现在调压绕组最大分接时的第34号线饼处,为49 038.50 N/m。其中三条曲线间距离较大,是因为调压绕组的接入对轴向漏磁影响较大,进而导致辐向短路力间的差别较大。

低压绕组沿绕组高度方向的辐向短路合力的变化趋势如图12所示。

图12 低压绕组辐向短路力合力随时间变化曲线

从图12可知,最大值出现在调压绕组最大分接时的第35号线饼处,为49 040.64 N/m.不同分接情况下第35号线饼上辐向短路合力随时间变化情况如图13所示。从图13可以看到,随着切向短路力变化趋势的不同,不仅会使得辐向短路力的大小发生变化亦会导致辐向力的变化趋势发生变化,而且切向力越大对辐向力的影响就越大。

随着单台变压器容量的增加和绕组中的电流增大,螺旋式绕组现今已经出现四螺旋、六螺旋,有的变压器调压绕组甚至采用八螺旋,这就使得螺旋升角远大于单螺旋。根据式(4)～(6)可知，切向短路力随着螺旋升角的增大而增大,也就是说其对辐向力的影响越来越大。

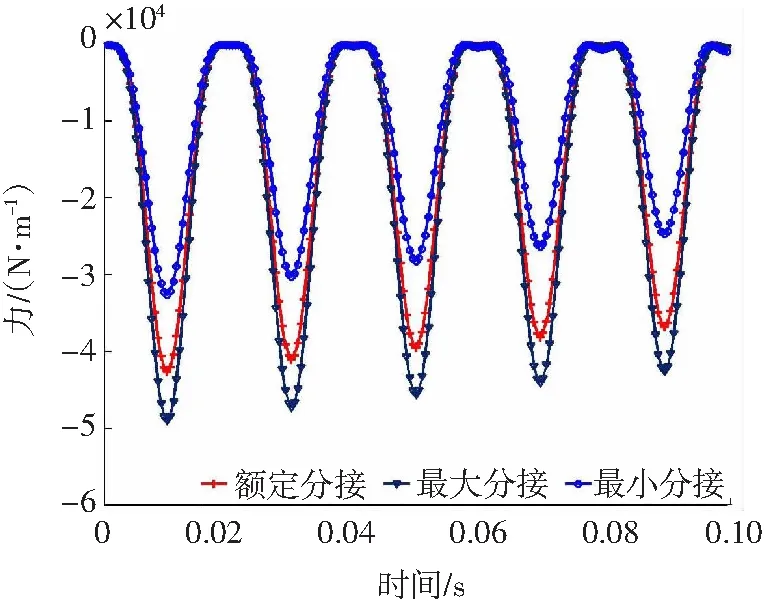
图13 低压绕组辐向合力随时间变化曲线

2.4 稳定性校核

变压器切向短路力的校核应以导线与其相接处的垫块间的摩擦力为准[9],如果切向短路力小于摩擦力说明螺旋式绕组在其作用下是稳定的,反之是不稳定的。摩擦力公式为

f=μFN

(7)

式中:μ为垫块与导线之间的摩擦系数,取0.07;FN为正压力,N。

对于变压器绕组,每个垫块上的压应力为

FN=pA

(8)

式中:p为垫块所受的预压紧力,Pa;A为垫块与导线间的接触面积,为4.53×10-3m2。

由式(7)、(8)可得摩擦力计算式为

f=μpA

(9)

由于调压绕组最大分接时的切向短路力最大,故校核螺旋式绕组的稳定性应采用该数据。由表1和表2中的数据可计算出实例变压器低压绕组两垫块间的距离为0.144 m,因而两垫块间的切向短路力为73.35 N。若想满足在螺旋式绕组切向短路力作用下大于工程要求,应留有一定裕度的安全系数1.8～2的稳定性,则螺旋式绕组两垫块间的摩擦力至少应大于132.03 N,代入式(9)有

故螺旋式绕组每个垫块上的压应力需大于0.416 MPa。绕组辐向失稳平均临界应力公式为[10]

(10)

式中:FB是辐向失稳临界力,kN/m;E是绕组导线弹性模量,为1.225×105MPa;x是每根自粘换位导线内并联导线根数;y是经验系数,为1.4;n是线饼中自粘换位导线根数;b是单根导线辐向宽度,m;t是单根导线轴向厚度,m;m是绕组有效支撑数,为实际撑条数的一半;R是低压绕组的平均半径,m。

将表1和表2中数据代入式(10)可求得低压绕组辐向失稳临界应力为74 695.43 N/m,大于实例变压器辐向短路合力的最大值,且安全系数为1.52,故在49 040.64 N/m的辐向短路合力作用下低压绕组是稳定的。

3 结 论

1) 磁力线在绕组端部弯曲严重,因而端部的辐向漏磁明显大于其他部位,且绕组与铁磁材料距离越远磁力线弯曲越明显。调压绕组的接入对变压器的轴向漏磁影响较大,对辐向漏磁的影响较小。

2) 随着螺旋升角的增大,切向短路力对辐向短路合力的影响亦越大。

3) 螺旋式绕组切向短路力使螺旋式绕组向内绷紧,若想满足在螺旋式绕组切向短路力作用下大于工程要求,应留有一定裕度的安全系数1.8～2的稳定性,则螺旋式绕组每个垫块上的压应力需大于0.522 MPa。

4) 由绕组辐向失稳平均临界应力公式可知,在49 040.64 N/m的辐向短路合力作用下低压绕组的稳定性良好。

[1] 王秀莲,唐任远,王胜辉.螺旋式绕组轴向电流对大型变压器漏磁场的影响[J].变压器,2002,39(1):1-6. WANG Xiulian,TANG Rengyuan,WANG Shenghui.Influence of axial current component in helical winding on leakage magnetic field in large transformer [J].Transformer,2002,39(1):1-6.

[2] 李航.大容量变压器绕组辐向稳定性分析[D].哈尔滨:哈尔滨理工大学,2015. LI Hang.Analysis of the large capacity transformer winding radial stability[D].Harbin:Harbin University of Science and Technology,2015.

[3] 张瑛,王胜辉,李岩.大型变压器螺旋绕组扭转电磁力的研究[J].沈阳工业大学学报,2006,28(6):610-613. ZHANG Ying,WANG Shenghui,LI Yan.Research on orsion electro-magnetic force of spiral winding in large transformers[J].Journal of Shenyang University of Technology,2006,28(6):610-613.

[4] 刘爽,孟庆民,洛君婷,等.大型变压器螺旋式绕组扭转问题的分析[J].变压器,2011,48(11):1-4. LIU Shuang,MENG Qingmin,LUO Junting,et al. Analysis of twist problem helical winding in large transformer[J].Transformer,2011,48(11):1-4.

[5] 于怀金,刘文里,王录亮.电力变压器绕组轴向短路力的研究[J].黑龙江电力,2011,33(4):260-264. YU Huaijin,LIU Wenli,WANG Luliang.Study on the winding axial short-circuit electromagnetic force in power transformer[J].Heilongjiang Electric Power,2011,33(4):260-264.

[6] 李阳阳.三绕组电力变压器绕组短路力计算[D].哈尔滨:哈尔滨理工大学,2013. LI Yangyang.Calculation on the windings short-circuit force for three-winding power transformer[D]. Harbin:Harbin University of Science and Technology,2013.

[7] 刘晓丽,刘文里,王明.基于“场-路”耦合法的电缆变压器轴向短路电磁力计算[J].黑龙江电力,2008,30(1):7-10. LIU Xiaoli,LIU Wenli,WANG Ming.Calculation of axial short-circuit electromagnetic force for cable transformer based on field-circuit coupling[J].Heilongjiang Electric Power,2008,30(1): 7-10.

[8] 王录亮.电力变压器绕组短路力计算[D].哈尔滨:哈尔滨理工大学,2012. WANG Luliang.Calculation on the windings short-circuit force of power transformer[D].Harbin:Harbin University of Science and Technology,2012.

[9] 褚微,梁作德,杜云霈,等.变压器的抗短路能力分析与计算[J].变压器,2013,50(12):1-7. CHU Wei,LIANG Zuode,DU Yunpei,et al.Analysis and calculation of ability to withstand short circuit of transformer[J].Transformer,2013,50(12):1-7.

[10] 谢毓城.电力变压器手册[M].北京:机械工业出版社,2003. XIE Yucheng.Power transformer manual[M].Beijing:Mechanical Industry Publishing House,2003.

(责任编辑 郭金光)

Calculation and analysis of radial short-circuit resultant force of helical winding in power transformer

LI Yichun1, LIU Wenli1, LI Jun2, BAI Shiguang1

(1.School of Electrical and Electronic Engineering, Harbin University of Science and Technology, Harbin 150080, China;2.Hali-Spitzer Automation & Control Technology (Shandong) Co., Ltd., Shanghai 201800, China)

On the basis of the principle of “circuit-field couple”, with the finite element software MagNet as a platform, aiming at the 80 000 kVA/110 kV double-winding on-load voltage regulating transformer, this paper respectively established the structure of 2D finite element model considering winding’s unbalanced ampere-turns with different tapping of voltage regulating winding. Considering the influence of non-linearity of core material, this paper adopted the nonlinear solver of the transient field to analyze the transient leakage magnetic field on the model, and calculated the transformer helical winding radial short-circuit force and tangential short-circuit force. On the syntheses of these force, in order to get the radial short-circuit resultant force and check the stability of transformer, this paper also calculated critical preloading force under the helical winding tangential short-circuit force to ensure the stability in transformer. The result shows that the theory and model succeed in calculating radial short-circuit resultant force and accounting radial mechanical strength.

transformer; helical winding; unbalanced ampere-turns; radial short-circuit force; tangential short-circuit force

2015-06-16。

李祎春(1990—),男,硕士研究生，主要研究方向为变压器绕组短路强度计算与稳定性分析。

TM401+.1

A

2095-6843(2016)02-0135-06