半刚性连接石油井架的动态特性研究
刘 冬,邹龙庆,付海龙
(1. 齐齐哈尔大学 机电工程学院,黑龙江 齐齐哈尔161006;2.东北石油大学 井架检测国家计量认证重点实验室,黑龙江 大庆 163318)
半刚性连接石油井架的动态特性研究
刘 冬1,2,邹龙庆2,付海龙2
(1. 齐齐哈尔大学 机电工程学院,黑龙江 齐齐哈尔161006;2.东北石油大学 井架检测国家计量认证重点实验室,黑龙江 大庆 163318)
为研究焊接节点的半刚性对钻机井架结构动态特性的影响,通过组件法计算了节点初始刚度和极限弯矩的理论值.采用双向变刚度零长度螺旋弹簧模拟节点的半刚性,建立了半刚接井架的有限元模型并进行了自振特性和谐响应分析.与刚接井架对比表明:节点的半刚性对井架结构固有频率影响显著,随着连接节点刚度的减弱,井架低阶固有频率值呈现不断减小的趋势,而井架侧移和前倾趋势则显著增加,给井架安全带来一定隐患.
半刚性;井架;动态特性 ;刚度
随着陆地深井、超深井和海洋油气钻探的迅速发展,油气田对石油井架钢结构承载性能的要求日益提高.过去几十年间,研究人员花费大量的精力研究钢结构整体的强度以及稳定性等问题,并取得了许多有益的成果.但是根据长期的实践经验,研究者发现,钢结构的破坏多数与局部出现损伤、腐蚀、焊接缺陷等因素有关,较少是由于结构整体强度或刚度的不足而引起的,钢框架破坏几乎都是从节点的破坏开始的.
石油井架属于典型的大承载钢架结构,主体结构是由大腿、拉筋等构件通过焊接、螺栓连接及销座耳板连接共3种方式连接而成,其中,焊接是井架结构中主要的节点连接方式.国内学者习惯上将井架各节点间的连接假定为完全刚性连接或者理想铰接形式,但实际上任何刚性连接都具有一定的柔性,而铰接都具有一定的刚性[1],井架各节点间的连接应介于这两者之间,属于半刚性连接.近年来国内外半刚性研究多集中在平面钢框架结构,对空间框架的研究很少,特别是对承载能力要求较高的石油井架结构,半刚性连接的研究更是寥寥无几.
大型钻机井架结构在承载作业时,不仅要承受提放钻具的大钩载荷,同时还要承受包括风载及钻机振动产生的振动载荷等多种载荷的作用[2].本文对梁柱焊接节点的初始转动刚度与极限弯矩进行了理论计算,以K型钻机井架为对象,研究在动载荷的作用下,节点的半刚性对井架结构动态特性的影响,为客观评价井架结构的抗风、抗震设计提供重要的理论基础.
1 半刚接井架有限元模型
1.1 节点初始转动刚度
井架主体由3~5段焊接结构组成,焊接节点在载荷作用下将承受和传递相当大的弯矩和剪力.假定弯矩全部通过翼缘焊缝传递到立柱上,且梁翼缘焊缝的受力均匀分布.焊接节点的构造如图1所示.

图1 梁柱焊接节点构造示意图Fig.1 Schematic diagram of welding joint structure
图1中θ为节点转角,通过组件法[3]计算焊接节点初始转动刚度(K),如式(1)所示.
(1)
式中:Kbf、Kcf、Kpz分别为梁翼缘焊缝等效剪切刚度、梁翼缘焊缝抗弯刚度及节点域的初始刚度.
(2)
(3)
(4)
式中:hb为梁截面的高度;Δs为梁水平位移;V为节点域处的剪力;I*为翼缘焊缝惯性矩;lw为翼缘焊缝宽度;Dc为立柱截面高度;tcw为立柱腹板厚度;tfb为梁翼缘厚度;E为钢材弹性模量;ED为焊缝弹性模量;γ为钢材泊松比.
悬臂梁端部加载弯矩值要在极限弯矩的范围内,极限弯矩公式采用平截面假定原则进行计算,得到平面内和平面外梁柱连接节点的极限弯矩公式如式(5)所示.
(5)
式中:Mu为节点的极限弯矩值;σs为梁翼缘焊缝的屈服强度.
1.2 半刚接井架有限元模型
JJ160/41-K型钻机井架主体结构由大腿、拉筋和连接节点构成,大腿和拉筋均采用BEAM 189单元模拟,拉筋端部节点通过一组具有3个转动方向的螺旋弹簧combin 39单元模拟与大腿之间的连接.节点的转动刚度值采用式(1)及焊接节点有限元模型(如图2所示)计算得到的数据,如表1所示,然后将节点的弯矩-转角关系曲线赋予弹簧单元中.令每个弹簧单元的长度为零,模拟拉筋与井架大腿之间的双向扭转,忽略拉筋自身受扭的影响.建立半刚接井架有限元模型如图3所示.

图2 箱型截面大腿-拉筋焊接节点模型Fig.2 Box type welded joint model

截面形式平面内极限弯矩/(kN·m)平面内转动刚度/(kN·m·rad-1)平面外极限弯矩/(kN·m)平面外转动刚度/(kN·m·rad-1)大腿L260mm×130mm×5mm61.202606.090.204742.0横拉筋L100mm×100mm×8mm7.02283.07.02244.3斜拉筋L100mm×63mm×6mm2.18130.45.03230.6

图3 半刚接井架有限元模型Fig.3 Finite element model of semi-rigid derrick
2 半刚接井架自振特性分析
当作用在井架上的动载荷频率与井架的某阶固有频率接近或成整数倍时,将引起井架结构的共振,这是产生井架倒塌的根本原因[4].为了研究半刚接节点对井架系统各阶固有频率和相应振型的影响,利用有限元软件对不同连接刚度的井架结构进行自振特性分析.表2给出了不同连接刚度下井架的固有频率值,其中K0为节点的初始转动刚度.

表2 不同连接刚度井架各阶固有频率值
由表2可见,JJ160/41-K型井架的基频是1.51 Hz,半刚性连接时井架各阶固有频率值明显小于刚性连接,伴随着连接节点刚度的减弱,井架低阶固有频率值呈现不断减小的趋势,刚度的降低对高阶频率值的影响则越来越弱.井架第1阶振型如图4所示.由图4可见,从低阶模态看,刚接与半刚接井架各阶的振型基本一致.在侧向yz平面内发生一定的弯曲振动,整体伴有绕y轴的扭转振动,二层台位置表现得尤为明显.

图4 井架第1阶振型Fig.4 Derrick first mode
3 半刚接井架谐响应分析
对井架结构进行谐响应分析,能够预测结构在稳态受迫振动下对不同频率载荷的响应特性.当钻机井架发生卡钻事故时钩载达到最大设计载荷,若同时再受到动载荷的作用则井架将陷入危险工况.为了研究此时井架的动态特性是否能满足安全要求,将最大钩载1 600 kN平均施加在井架顶部的4个节点上,对两种连接形式井架施加相同荷载、约束条件,分别获得刚接与半刚性连接井架前开口顶部节点x轴方向的位移响应曲线如图5和6所示.
井架系统的主振方向为前开口方向,1.82 Hz为井架危险工况时的主要共振频率.由图5和6可知,当达到共振频率时,刚接井架的最大位移为72.021 cm,半刚接井架的最大位移达到91.358 cm.

图5 刚接井架顶部节点频率-位移响应曲线Fig.5 Displacement response curve of the top node for the rigid derrick

图6 半刚接井架顶部节点频率-位移响应曲线Fig.6 Displacement response curve of the top node for the semi-rigid derrick
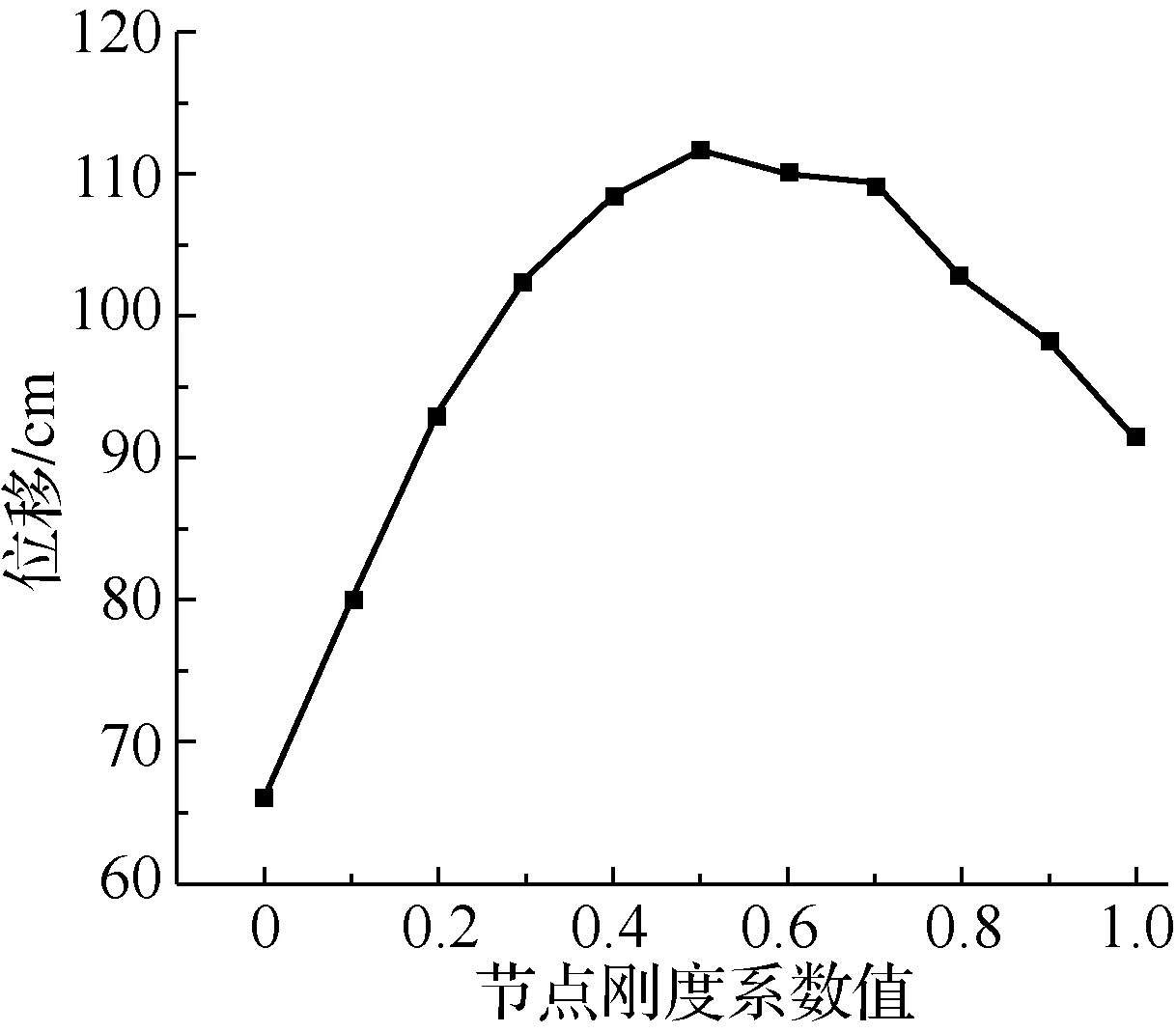
图7 不同刚度下井架前开口顶点位移Fig.7 Displacement of the top of the derrick with different rigidity values
图7给出了不同连接刚度下井架前开口顶点的位移.由图7可知,在动载荷的作用下,当节点刚度在一定的范围内下降时,半刚接井架的最大位移响应有增大的趋势.说明半刚接节点的存在会增大井架侧移和前倾趋势,在后期振动中表现得更加明显.这是由于半刚接节点具有一定的转动自由度,结构具有较好的延性和耗能能力,半刚接井架的塑性变形能力要强于刚性连接井架,将更有利于抵抗动载荷的作用[5],但同时也使井架稳定安全系数降低,位移的增大易引发井架失稳倒塌事故.
当节点的刚度降到一定值以后,最大位移响应又有不断减小的趋势,其共振频率对应的位移值并不一定大于刚接井架.节点的刚度变化对井架结构的动力响应的影响没有特定的规律,这与静力分析中位移与结构的刚度总是成反比不同,动力分析中响应和刚度关系更为复杂[6].
4 有限元模型的试验验证
井架振动测试仪器由TS3828型动态应变仪、UT3232S型数据采集器、UTekl型软件包及笔记本电脑组成,分别对井架进行动态载荷测试和模态参数测试.动态载荷测试采用BJ115-10AA型应变计布置在井架每根大腿的上下层两处位置. 共有32个测点;模态测试采用TS1102/1100型加速度传感器布置在井架大腿上中下5处位置.井架的结构简图及应变计和传感器的具体布置方案如图8和9所示.
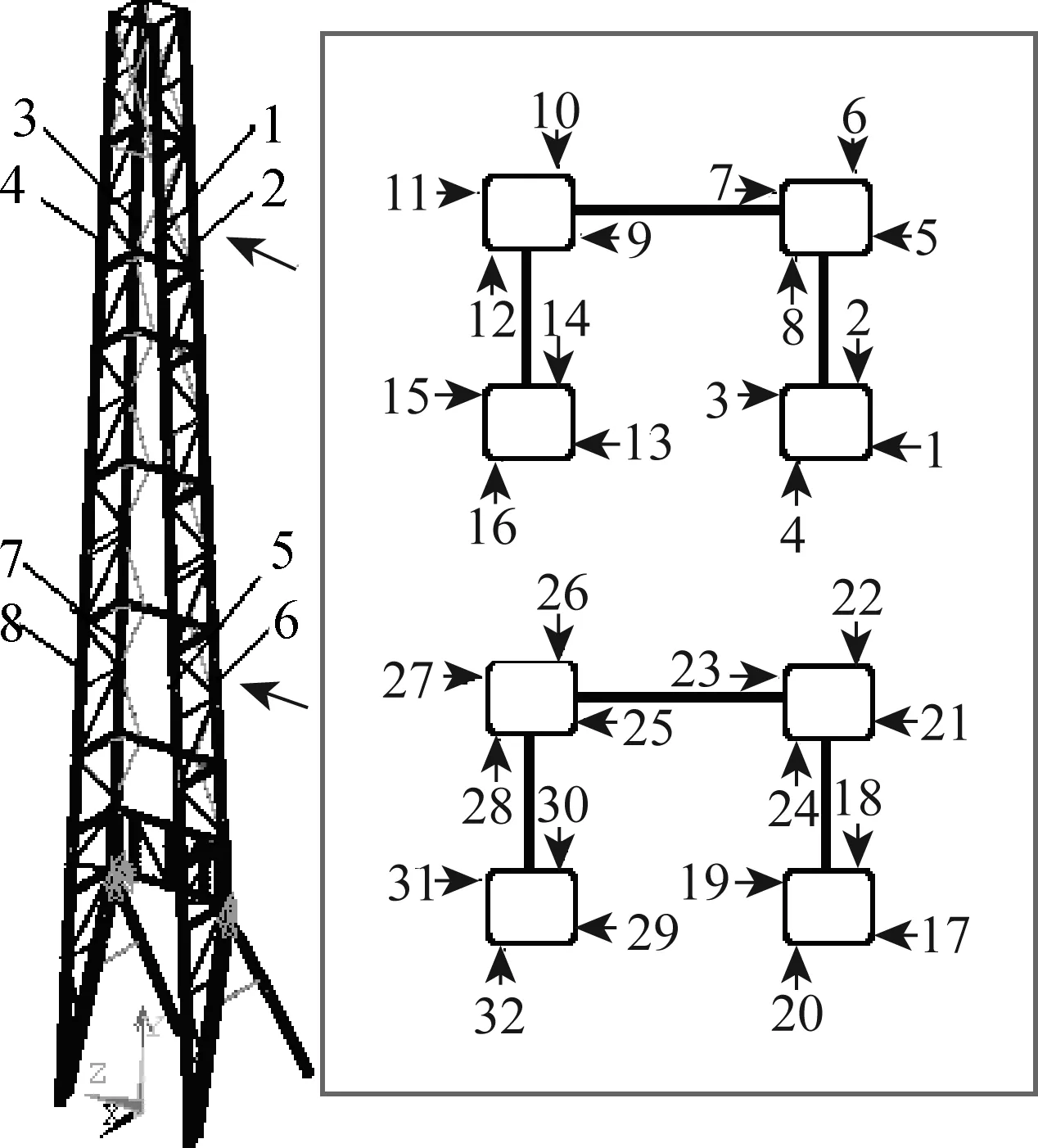
图8 井架动载测试应变计布置方案Fig.8 Arrangement scheme of dynamic load test for derrick

图9 井架模态测试传感器布置方案Fig.9 Arrangement scheme of modal test for derrick
对井架动载测试得到的多组数据曲线进行分析,通过转换得到最大应力和应变值.为验证半刚接井架有限元模型的准确性,通过测试数据与有限元仿真结果的对比进行判断.在测试钩载为56.84 kN下,井架1~8号大腿处测试应力和模拟应力结果的对比如表3所示.

表3 测试应力及仿真模拟应力值
由表3可知,井架动载测试与仿真试验结果的拟合相对误差均在5%以内,从静力学方面验证了所建立的半刚接井架有限元模型的准确性.对井架进行模态参数测试[7],识别得到该钻机井架的一阶固有频率为1.438 Hz,与半刚性连接时井架一阶固有频率值非常接近,从动力学方面也验证了该井架模型的正确性.振动测试结果与仿真试验结果对比表明,实际工况下,井架各节点间处于半刚性连接状态,用组件法计算得到的节点刚度和极限弯矩值是合理的,模拟井架半刚性连接的方法是可行的,与现场真实井架结构基本一致.利用半刚接井架有限元模型进行的静、动力相关的计算,所得的结论具有一定的参考价值.
5 结 论
(1) 半刚性连接分析中,弯矩-转角关系最能反映连接变形与荷载之间性能.用螺旋弹簧来模拟节点柔性对梁单元的影响,通过组件法推导了井架大腿与拉筋之间的焊接节点初始刚度的理论计算公式,获得了节点弯矩-转角关系.
(2) 通过对不同连接刚度井架结构的自振特性分析表明,节点的半刚性对井架结构的固有频率影响显著.随着节点刚度的降低,井架结构的低阶固有频率呈现不断减小的趋势,刚度的降低对高阶频率值的影响则越来越弱.因此,将井架按照刚接结构进行设计将造成较大的安全隐患,必需考虑到节点的柔性对其结构动力特性的影响.
(3) 在持续周期性简谐载荷作用下,节点转动刚度在一定的范围内降低时,会增加井架结构的侧移和前倾趋势,严重的将引起井架失稳倒塌;当节点的转动刚度降到一定值以后,半刚性连接井架的共振频率对应的位移值并不一定大于刚接井架.因此对于钻机井架安全评定时,焊接节点半刚性的影响不容忽视,同时还要考虑动载荷的具体种类、激励形式、结构本身特性等多重因素的影响,为油田作业安全生产提供可靠的理论依据.
[1] 舒兴平,袁智深,张再华,等.半刚性连接钢结构理论与设计研究的综述[J].工业建筑,2009,39(6):13-21.
[2] 邹龙庆.石油钻机井架动态响应分析[D].哈尔滨:哈尔滨工程大学船舶工程学院,2006.
[3] 邹龙庆,刘冬,崔晓华.石油井架结构焊接节点的刚度计算[J].石油矿场机械,2012,41(2):17-20.
[4] 赵焕娟,齐明俠,赵娜.钻机井架可靠性分析[J].石油矿场机械,2010,39(3):22-27.
[5] HONG K,YANG J G,LEE S K. Parametric study of double ang1e framing connections subjected to shear and tension [J].Journal of Constructional Steel Research,2001,57(6): 997-1013.
[6] 孙修礼,王永明,管毅,等.半刚性连接框架结构的动力响应分析[J].工程抗震与加固改造,2007,29(4):18-22.
[7] 刘金梅.在役钻机井架使用安全性综合评价方法研究[D].大庆:东北石油大学机械科学与工程学院,2012.
Study on the Dynamic Response of Oil Derrick Structure with Semi-rigid Joints
LIUDong1, 2,ZOULong-qing2,FUHai-long2
(1. School of Mechanical and Electronic Engineering, Qiqihar University, Qiqihar 161006,China;2. State Key Laboratory of Metrological Authentication for Petroleum Drilling Derrick,Northeast Petroleum University,Daqing 163318,China)
In order to study the influence of semi-rigid joints on the dynamic characteristics of the mine derrick structure, the theoretical calculation formula of the stiffness and ultimate moment of the welded joint between the derrick and the joints are obtained by the component algorithm. The zero-length spiral spring with dual direction and variable stiffness is applied to simulate the semi-rigid joints, the finite element model of semi-rigid derrick is established, the harmonic response analysis and the natural vibration characteristics are carried out. By comparing with the rigid connection, semi-rigid joints have a significant effect on the natural frequency of the derrick structure. With the decrease of the stiffness of the joints, the natural frequency of the derrick structure decreases and the derrick lateral displacement and the forward tendency significantly increase, which bring some safe trouble to the derrick.
semi-rigid; derrick; dynamic characteristics; stiffness
1671-0444 (2016)04-0518-05
2015-12-21
国家科技支撑计划资助项目(2012BAH28F00);黑龙江省自然科学基金资助项目(E201409);齐齐哈尔大学教育科学研究资助项目(2015054)
刘 冬(1986—),男,黑龙江大庆人,讲师,博士研究生,研究方向为大型钢结构的设计、承载能力与检测以及安全评定工作. E-mail: liudong224@126.com
TE 923
A

