双压力角非对称齿形直齿面齿轮副有限元应力分析
张淑艳,郭 辉,张蒙祺, 孙晓玲
(1. 西安建筑科技大学 理学院,陕西 西安 710055;2. 西北工业大学 机电学院,陕西 西安 710072;3. 空间物理重点实验室,北京100076)
双压力角非对称齿形直齿面齿轮副有限元应力分析
张淑艳1,郭 辉2,张蒙祺2, 孙晓玲3
(1. 西安建筑科技大学 理学院,陕西 西安 710055;2. 西北工业大学 机电学院,陕西 西安 710072;3. 空间物理重点实验室,北京100076)
根据齿轮啮合原理,推导了双压力角非对称齿形面齿轮的齿面方程.在有限元软件ANSYS中建立了面齿轮副轮齿接触有限元分析模型.通过有限元接触压力计算结果与基于点接触Hertz理论接触压力计算结果的对比分析,确定了有限元模型的网格密度.由若干组算例的计算结果表明,适当增大工作侧齿面压力角可以明显降低面齿轮副接触压力和齿根弯曲应力,因此,非对称齿形设计可以获得更高的轮齿强度.
非对称设计;面齿轮传动;有限元法;齿面接触压力;齿根弯曲应力
面齿轮传动具有结构紧凑、传动比大等优点,近年来已被应用于航空减速器[1]等高速重载及有轻质要求的场合.然而面齿轮齿宽受到外径齿顶变尖和内径根切的限制,使其轮齿强度受到一定的影响.
文献[2]研究表明,适当增加齿轮压力角可以降低齿面接触压力,提高抗胶合能力.但当压力角增大时,齿轮齿顶会变薄并使强度下降.鉴于航空减速器中齿轮副通常是单向传动,故可以尝试将面齿轮的工作侧齿面压力角增大,而将非工作侧齿面压力角适当减小.这样既可以提高齿面强度,又可以保证足够的齿顶厚度,如此便形成了双压力角非对称面齿轮副.
在面齿轮齿形设计与啮合性能分析方面,国内外已有不少文献报道相关研究.文献[3]推导了面齿轮齿面方程,建立了齿面双冠修形方法,通过TCA(tooth contact analysis)和接触有限元分析研究了修形量对啮合性能的影响.在非对称齿形设计方面:文献[4]对非对称齿形直齿轮齿面生成及齿面修形方法进行了讨论;文献[5]研究了非对称齿形直齿轮设计参数(非对称系数等)的可行域,并在某型直升机中得以应用,齿轮强度提高了5%~9%.国内方面,文献[6-7]对面齿轮的设计和加工技术进行了研究,文献[8]采用有限元法研究了标准直齿面齿轮副的应力变化规律,文献[9-10]研究了面齿轮的磨齿加工理论和方法.
本文主要探讨非对称齿形设计对面齿轮副强度性能的影响,分析齿轮应力随参数的变化规律,以求获得面齿轮副更高的强度性能.
1 非对称齿形直齿面齿轮齿面的生成
为了进行有限元应力分析,首先要建立非对称齿形直齿面齿轮齿面的准确几何模型.然而面齿轮的齿面形状非常复杂,无法用显式表达式表示,同时为了研究齿形参数对强度的影响,因此,这里先给出非对称面齿轮两侧齿面方程的推导过程.其基本思路:以基本齿条工作侧和非工作侧的齿面方程为基础,推导用于展成面齿轮的产形(由刀刃切削运动产生的形状)圆柱齿轮两侧齿面,再根据产形轮齿面和运动学法,推导非对称齿形面齿轮的两侧齿面.
1.1 非对称齿形插齿刀齿面方程
面齿轮传动原本为线接触形式,但如果产形轮齿数比与其啮合的小齿轮大ΔN,便可获得点接触,通常取ΔN=1~3.
产形轮齿面的生成坐标系设置如图1所示,动坐标系Ss(Os-xs-ys-zs)、Scs(Ocs-xcs-ycs-zcs)分别与产形轮和齿条刚性联结,静坐标系Sm(Om-xm-ym-zm)与刀架刚性联结.渐开线齿轮对称齿条形刀具的基本齿廓是齿形角等于标准压力角的梯形齿廓;而非对称渐开线齿轮的基本齿廓保持分度线上的齿厚不变,改变两侧刀刃的压力角使之不再相等.

(a) 齿条法向齿形 (b) 齿条齿向齿形 (c) 展成运动图1 由非对称齿条展成圆柱直齿轮的坐标系示意图Fig.1 Systems for generation of spur gears by asymmetric race-cutter
在坐标系Scs下齿条工作侧与非工作侧的齿面方程分别为
(1)
(2)
式中:αnd,αnc分别为齿条工作侧与非工作侧的压力角;s0为齿条节面处的齿槽宽,它决定了被展成齿轮的节圆齿厚;usd,usc,lsd,lsc分别为齿条工作侧及非工作侧齿面在齿廓方向与齿条宽度方向的两个齿面参数.
在Scs坐标系下齿条两侧齿面的法向量分别为
(3)
(4)
根据啮合原理[11],产形轮两侧齿面的径矢方程与法矢方程可分别表示为
(5)
(6)

Lscs(φs)为Mscs(φs)的前三行三列所构成的向量转换矩阵;rps为产形轮分度圆半径;φs为产形轮的转角;fd(usd,lsd,φs)与fc(usc,lsc,φs)分别为两侧齿面在展成过程中的啮合方程.
1.2 非对称齿形面齿轮齿面方程
为便于分析,建立如图2所示的坐标系统.其中:坐标框架Ss与S2分别被刚性地连接在产形齿轮与面齿轮上;坐标系Sm与Sa是两个辅助的固定坐标框架,Sa位于刀具的初始位置上,辅助固定坐标系Sm位于面齿轮的初始位置上;角度ψs和ψ2分别为刀具齿轮和面齿轮的转角;γm为面齿轮副的轴交角;L0为辅助参数,其值可取为面齿轮的内半径.
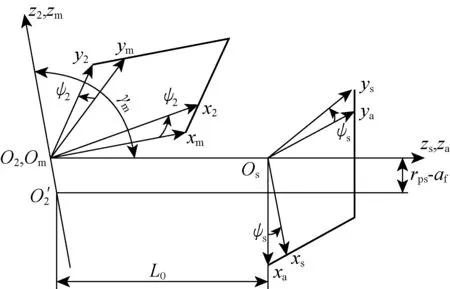
图2 面齿轮加工坐标系Fig.2 Coordinate systems for generation of face gear
从产形轮固结坐标系Ss到面齿轮固结坐标系S2的坐标转换矩阵为
根据微分几何原理可以通过如下方式推导工作侧啮合方程,非工作侧与此同理.在与产形轮固结的Ss坐标系中,产形轮上任意一点相对于面齿轮的相对速度为
(7)
由式(5)可得到产形轮在Ss坐标系中的齿面方程及法向量,由齿轮啮合原理,齿面在接触点的相对运动速度与公法矢量方向相垂直,即两齿面沿接触点的公法线方向无相对运动,可得啮合方程为
(8)
把产形轮在Ss坐标系下的齿面通过坐标转换表示为在S2坐标系下随运动参数ψs变化的曲面,即:
r2d(usd,lsd,ψs)=M2s(ψs)·rsd(usd,lsd)
(9)
r2d(usd,lsd,ψs)中的点作为面齿轮齿面,除了满足式(9)外,还需满足啮合方程(8),即面齿轮齿面方程可表达为如下方程组的形式:
(10)
方程组(10)内包含3个变量usd,lsd和ψs,由啮合方程可消去参数ψs,进而构成一个含2个参变量(usd,lsd)的曲面方程.
同理,非工作侧齿面方程为
(11)
方程组(11)的第二项为非工作齿面与相应产形齿轮齿面间的啮合方程,其形式与式(8)类似,这里不再给出推导过程.
2 有限元模型的建立及网格密度
2.1 有限元接触计算模型
以面齿轮齿面方程组(10)和(11)为基础,在两侧齿面区域内沿齿高方向和齿宽方向均匀采点,然后按照一定规律生成轮齿内部的节点和单元.图3为面齿轮副单齿的有限元网格示意图,为了真实反映齿根处的应力集中,齿根部位进行了网格细化处理.
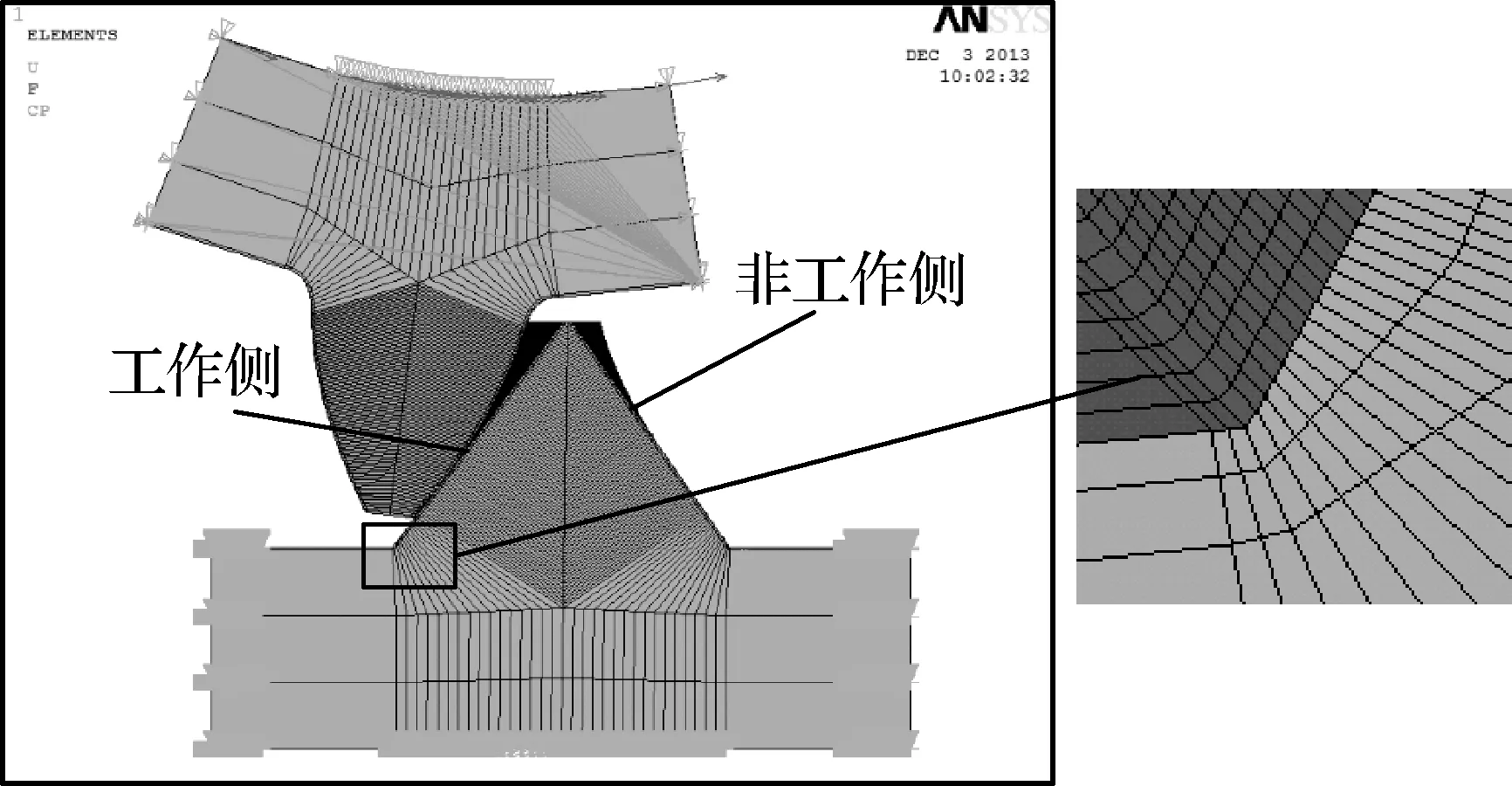
图3 面齿轮驱动有限元接触计算模型Fig.3 FEM contact model of face gear drive
图3所示面齿轮副的基本参数以及施加载荷数据如表1所示.在此模型中,约束面齿轮轮齿底面和左右侧面的所有自由度,约束小齿轮底面和左右侧面除绕轴线旋转以外的所有自由度;面齿轮副受到的力矩载荷以切向力的形式施加在位于小齿轮底面的节点上.由接触计算可同时获得接触应力分布和齿根弯曲应力的分布,如图4所示.

表1 面齿轮副参数表

图4 面齿轮齿面接触应力分布Fig.4 Contact stress distribution of face gear
2.2 网格密度讨论
在有限元计算中,由于数值问题导致网格的疏密程度对计算结果有一定的影响.一般而言,网格越密则计算结果越精确,但耗费的计算时间会相应大量增加.为了平衡计算精度与计算时间,本文建立了标准齿形面齿轮单对轮齿接触模型(如图3所示),将单对轮齿有限元计算的接触压力最大值与根据点接触Hertz理论计算的接触压力[12]最大值进行对比,结果如表2所示.

表2 两种方法计算值对比表
由表2可知,随着网格密度增加,接触压力FEM计算值呈现趋向于某定值的态势.当网格密度为齿宽方向200个单元、齿廓方向100个单元时,Hertz理论计算值与FEM计算值的相对误差已在5%以内.由于点接触Hertz理论在适用于齿轮接触问题时本身存在一定的误差,所以当Hertz理论计算值与FEM计算值的相对误差在5%以内时,可以认为有限元计算方法已经达到了足够高的计算精度.
3 非对称齿形面齿轮副轮齿应力分析
仍以表1所述参数的面齿轮副为对象进行应力分析.为了研究两侧压力角的变化对面齿轮副各项应力值的影响情况,这里将算例分为两大组,编号为1~6的算例为第一组,仅改变工作侧压力角αnd取值,编号为7~12的算例为第二组,仅改变非工作侧压力角αnc取值,如表3所示.

表3 面齿轮副压力角取值表
对于每一种压力角组合,均计算了位于从面齿轮齿顶到齿根的不同啮合位置处的各项应力值,结果如图5和6所示.各个啮合位置以图5和6中的横坐标“接触位置编号”区分,编号值越小越靠近面齿轮齿顶.当轮齿处于不同啮合位置时,各项应力值是不同的.为了对不同参数齿轮副的应力能够进行比较,本文使用轮齿接触分析(TCA)技术[6],通过调整大小轮的安装角度,将所有算例中小齿轮接触点限定在相同半径处.

(a) 齿面最大接触压力
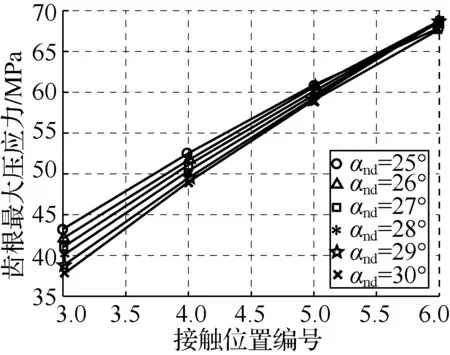
(b) 齿根最大压应力

(c) 齿根最大拉应力图5 仅改变工作侧压力角时应力变化(算例1~6)Fig.5 Stress variations for different pressure angles in drive side (case 1 to 6)
由图5和6可知,当改变单侧压力角时,各项应力值随压力角在每个接触位置基本呈线性变化.压力角变化时有以下规律:

(a) 齿面最大接触压力

(b) 齿根最大压应力

(c) 齿根最大拉应力图6 仅改变非工作侧压力角时应力变化(算例7~12)Fig.6 Stress variations for different pressure angles in coast side (case 7 to 12)
(1) 增大工作侧压力角时,齿面最大接触压力显著下降(平均降幅9.40%),齿根最大压应力显著下降(平均降幅7.43%),齿根最大拉应力显著下降(平均降幅10.96%);
(2) 减小非工作侧压力角时,齿面最大接触压力基本不变(最大变化幅值1.50%,变化均值0.25%),齿根最大压应力基本不变(最大变化幅值2.00%,变化均值0.82%),而齿根最大拉应力有小幅上升(平均升幅2.93%).
4 结 语
本文对双压力角非对称齿形直齿面齿轮副的承载能力进行了研究,探讨了压力角对齿面接触压力和齿根弯曲应力的影响,主要结论有:
(1) 增大工作侧压力角可以明显降低接触压力和齿根拉压应力,提高轮齿的静强度;
(2) 非工作侧压力角对接触压力以及齿根压应力基本没有影响,对齿根拉应力有较小程度的影响.
[1] FILLER R R, HEATH G F, SLAUGHTER S C, et al. Torque splitting by a concentric face gear transmission[C]//The American Helicopter Society, 58th Annual Forum. Montreal Canada, 2002.
[2] DENG G, NAKANISHI T. Bending load capacity enhancement using an asymmetric tooth profile[J]. JSME International Journal, 2003,46(3):1171-1177.
[3] LITVIN F L, FUENTES A, ZANZI C, et al. Face-gear drive with spur involute pinion: Geometry, generation by a worm, stress analysis[J]. Computer Methods in Applied Mechanics and Engineering, 2002, 191: 2785-2813.
[4] LITVIN F L, LIAN Q, KAPELEVICH A L. Asymmetric modified spur gear drives: Reduction of noise, localization of contact, simulation of meshing and stress analysis[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 188(1/2/3): 363-390.
[5] KAPELEVICH A. Geometry and design of involute spur gears with asymmetric teeth[J]. Mechanism and Machine Theory, 2000, 35(1):117-130.
[6] 郭辉, 赵宁, 方宗德, 等. 基于接触有限元的面齿轮传动弯曲强度研究[J]. 航空动力学报, 2008, 23(8): 1438-1442.
[7] 李政民卿, 朱如鹏. 基于包络法的正交面齿轮齿廓尖化研究[J]. 中国机械工程, 2008, 19(9): 1029-1033.
[8] 唐进元, 刘艳平.直齿面齿轮加载啮合有限元仿真分析[J]. 机械工程学报, 2013,48(5):124-131.
[9] 郭辉, 赵宁, 侯圣文. 基于碟形砂轮的面齿轮磨齿加工误差分析及实验研究[J]. 西北工业大学学报, 2013, 31(6): 915-920.
[10] 彭先龙, 李建华, 方宗德, 等. 碟形砂轮磨削面齿轮的数控规律[J]. 哈尔滨工业大学学报, 2012, 44(11):101-104.
[11] 吴序堂. 齿轮啮合原理[M]. 2版. 西安:西安交通大学出版社, 2009:97-102.
[12] 郭辉. 面齿轮滚齿加工方法及其啮合性能研究[D]. 西安: 西北工业大学机电学院,2009.
FEM Stress Analysis of Spur Face Gear Pair with Asymmetric Double Pressure Angles
ZHANGShu-yan1,GUOHui2,ZHANGMeng-qi2,SUNXiao-ling3
(1. School of Science, Xi’an University of Architecture & Technology, Xi’an 710055, China;2. School of Mechatronics, Northwestern Polytechnical University, Xi’an 710072, China;3. Key Laboratory of Space Physics, Beijing 100076, China)
The equations of tooth surface of double pressure angles asymmetric face gear were conducted according to the theory of gearing. A contact finite element model was established in software ANSYS. The contact pressure calculated from finite element model and the calculated value of contact pressure which was given by the point-contact Hertz theory were compared to determine the element density of the finite element model. Several groups of parameters were calculated. The results show that appropriate increment of the pressure angle of driving side can obviously decrease contact pressure and root bending stress of face gear. Therefore, the applying of asymmetrical design can improve the static load capacity of face gear.
asymmetric design; face gear drive; finite element method; contact pressure of tooth surface; bending stress of tooth root
1671-0444 (2016)04-0490-06
2015-02-05
国家自然科学基金资助项目(51475352);中央高校基本科研业务费专项资金资助项目(3102015BJ(II)MYZ28)
张淑艳(1979—),女,内蒙古赤峰人,副教授,博士研究生,研究方向为机械传动、计算机图形学. E-mail: zhsy1227@163.com
TH 132.41
A

