基于RBF神经网络的地铁振动预测分析

王秀丽，潘 雷，彭桂力，梁 茵，王贝贝

(天津城建大学 a. 控制与机械工程学院；b. 能源与安全工程学院，天津 300384)

城市交通

基于RBF神经网络的地铁振动预测分析

王秀丽a，潘 雷a，彭桂力a，梁 茵b，王贝贝a

(天津城建大学 a. 控制与机械工程学院；b. 能源与安全工程学院，天津 300384)

随着城市地下轨道交通的大力发展，列车运行引起的环境振动及噪声对周边环境及人们生活的影响越来越大．如何准确预测地铁列车引起的振动，有效分析振动的传播规律，为减振降噪提出有价值的参考数据就显得尤为重要．实测的振级数据是引起地铁列车振动的所有因素的综合效应，隐含了地铁振动的规律．以实测的振级数据为样本，结合滑动窗口技术构建径向基神经网络预测模型，得出了振级的拟合曲线，实现了对振动峰值的预测．通过实例说明，预测效果良好，建立的预测模型能充分反映地铁振动系统的非线性函数的映射关系．

地铁振动；加速度振级；径向基神经网络；预测

城市轨道交通运行产生的振动常常会影响邻近居民生活的舒适性．随着人们生活水平的提高，人们对居住环境的质量要求也越来越高，因而使得这一问题越发凸显出来．

针对实际工程，国内外学者进行了大量与振动舒适度相关的研究．郑薇[1]用数值的方法模拟了杭州火车站附近某建筑物在列车经过时的动力响应，采用总体频率计权曲线对建筑物的振动舒适度进行了评价；丁洁民等[2]以上海地铁1号线附近某拟建建筑为研究对象，用数值模拟的方法计算该结构在实测地面振动加速度输入下的动力响应，并基于烦恼率的方法评价振动舒适度；张晓春等[3]通过建立隧道及地面建筑三维有限元模型，计算了地面建筑的动力响应，利用模糊理论和统计方法得出以人们对振动的不满率作为烦恼率评价的方法；何浩祥等[4]通过小波包变换计算加速度振级，进而按照ISO 2631评价人体舒适度；蒋通等[5]将楼板简化为单自由度体系，将地铁引起的建筑物内房间墙根的竖向振动加速度时程作为该自由度体系的基底输入，获得加速度响应，并以此作为楼板间的振动响应，提出了一种用于分析和预测地铁引起邻近建筑物楼板振动的简化可行的计算方法．Hirokazu Takemiya[6]建立了瑞典Ledsgard高速列车轨道的仿真模型，并利用该模型实现了火车经过时引起的地面振动的预测．

如上所述，对地铁振动系统的评价绝大多数是建立在数值模拟计算和对三维有限元模型分析的基础上，并没有给出如何实现对振动系统振级等参数的预测．由于地铁振动是一个复杂的多因素相互影响的综合效应[7]，这就使得对地铁振动系统的预测评估很难通过简单的数值模拟计算得到．

若假定影响振动系统的各种性能参数都确定时，系统的响应也是一定的，那么关键就在于如何才能更近似地表达这种关系[8]．实际测量的数据包含了影响振动系统各种因素的所有信息，因此从实测的振动数据出发建立的系统模型，就能够真实地反映振动系统实际的输入与响应之间的函数关系．径向基RBF神经网络是一种前馈型神经网络，在理论上具有任意逼近性能和最小特性，可用于各种数据的预测中[9-10]．将RBF神经网络结合窗口滑动技术应用于轨道振动分析中，利用实测的振级数据作为网络的训练样本和检验样本，能较好地实现振级的网络拟合和预测．

1 原始数据分析和处理

1.1 原始数据分析

原始数据监测站点属于1类振动环境功能区，该功能区的环境振动Z振级VLZ限值昼间为70,dB，夜间为65,dB，此限值适用于稳态振动、冲击振动和无规振动．根据标准[11]规定：每日发生的冲击振动最大值不得高于环境振动限值幅度昼间10,dB，夜间3,dB．

评价建筑物受地铁环境振动的影响时以铅垂方向的振动为主[12]．对于环境振动，人体对1～80,Hz的振动最为敏感．频率一定，振幅越大，影响越大．人刚刚感觉到的垂直振动为60,dB，不可忍耐的振动为114,dB．振动加速度达到 65,dB 时，对睡眠有轻微影响；振动加速度达69,dB时，所有处于轻度睡眠状态的人将被惊醒；振动加速度达74,dB时，除深度睡眠状态的人外都将被惊醒；而达到79,dB时，所有的人都将被惊醒[3]．

为了从数目庞大的原始数据中合理地选择出神经网络训练和测试所需的样本，并保证以此为基础构建的网络模型的有效性，对不同频率下的原始振级数据进行了比较，得出的数据曲线如图1所示．由图1可知，曲线周期大约为6,min；在每个周期中，5，20,Hz的振动加速度均没有超过53,dB；列车到站时，在80,Hz出现了冲击振动，振动加速度约为78.1,dB，而其它时间大部分在40,dB以下；50,Hz的振级在整个周期内均在47,dB 以上，并在列车到站时出现冲击振动，此时振级约为66,dB．通过对比，选取整个周期振级均值较大的50,Hz频率下的振动数据进行分析．

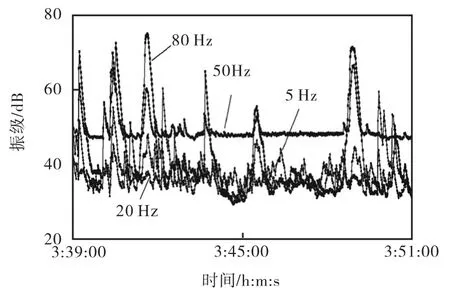
图1 原始振动数据

1.2 数据处理

1.2.1 时间转换

原始数据中，时间的格式为时：分：秒，为了使时间格式便于归一化处理，因此首先把时间数据转换成单位为小时的数据，然后在此基础上再进行归一化处理．

1.2.2 样本数据归一化

由于网络的输入变量是一组由时间和振级构成的样本，二者单位不同．为了避免因为样本数据单位的不同而对神经网络模型构建产生影响，首先应对各样本集进行归一化处理，归一化之后振级和时间均在(0，1)之间，归一化公式为

式中：x_1i为xi归一化之后的值；min(Y)为Y的最小值；max(Y)为Y的最大值；Y为xi所在的向量．

1.2.3 反归一化过程

通过上述的归一化处理，训练样本、检验样本及网络的输出均为(0，1)内的数值．为了便于通过图形曲线更加直观地分析网络模型性能及地铁振动数据的规律，还需要对相应数据进行反归一化处理，反归一化公式为

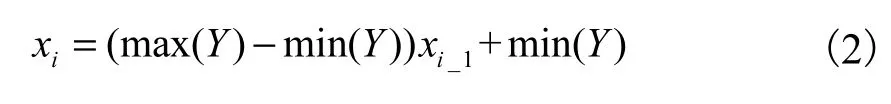
2 RBF神经网络的建立

2.1 RBF神经网络模型结构

RBF神经网络是由输入层、隐含层和输出层构成的多输入单输出系统，隐含层实现特征提取，输出层实现输出权值的线性组合[13]，其结构如图2所示．

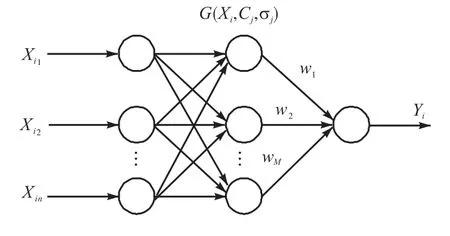
图2 RBF神经网络模型结构

设RBF神经网络的输入为n维，学习样本为(X，Y)，其中X＝(X1，X2，…，XN)，N为训练样本数；输入变量Xi＝(Xi1，Xi2，…，Xin)T，1iN≤≤；期望输出Y＝(Y1，Y2，…，YN)；在构建RBF神经网络时，若输入变量为Xi＝(Xi1，Xi2，…，Xin)T时，对应的期望输出为Yi＝Xin＋1；对全体输入学习样本，网络输出为

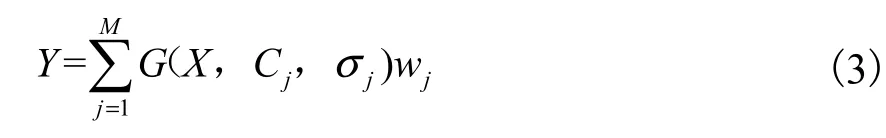
式中：G( X，Cj，σj)为隐含层第j个节点的输出，Cj=(cj1,cj2,…,cjn)T为第j个隐含层高斯函数的中心；σj为第j个隐含层高斯函数的宽度；wj为第j个隐含层节点与输出层之间的网络连接权；M为隐含层节点数．

2.2 样本的构建

在神经网络模型构建过程中，样本的选取是关键．因为样本数据的数量和质量在很大程度上直接影响到神经网络的泛化性能，因此选择出的样本数据必须具有代表性，能体现原始数据集的整体特征[14]．将滑动窗口技术[15]引入到样本的选取中，利用数据之间的关联性，取前N个时刻数据作为训练样本，预测出第N＋1或者是第N＋K的振级及对应的时间．

3 基于RBF神经网络的振级预测

由于地铁列车工作日与双休日运营时间不同，但又为了反映工作日及双休日列车的振动规律，因此构建了两个RBF神经网络．

3.1 工作日地铁振级的RBF神经网络模型构建与测试

将2014-09-18(周四)T13：34-14：06的数据，每3,s取一个，作为网络的训练样本进行网络模型的构建，拟合工作日地铁振级曲线；将2014-09-19T13：34-13：49及17：00-17：15两个时段和2014-09-20T 13：34-13：54的数据用于网络测试．

在网络训练过程中，每组训练样本的前6个作为学习样本，第7个作为期望输出，依此建立循环，确定学习样本和期望输出．通过试验发现拟合曲线误差较小，但网络测试误差很大，因此调整了对期望输出的选取．由于相邻3,s的振级数据变化不大，因此将每组学习样本中的第6个作为期望输出，这样调整后，网络的拟合误差和测试误差都较小．表1-2给出了神经网络训练过程中设定的相关参数及网络训练完成后的相关权值和阈值．分析曲线如图3-9所示．

表1 神经网络训练参数

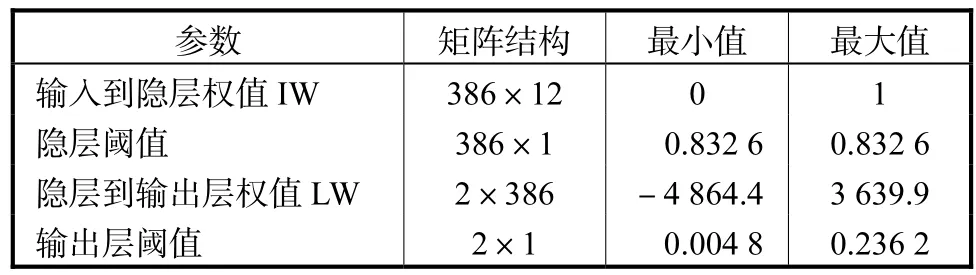
表2 神经网络训练后权值与阈值

图3反映了网络拟合误差在±0.001,5,dB之间，拟合效果很好．图4反映了以19日13：34-13：49振级作为测试样本的测试误差曲线，网络测试绝对误差最大约为0.35,dB．

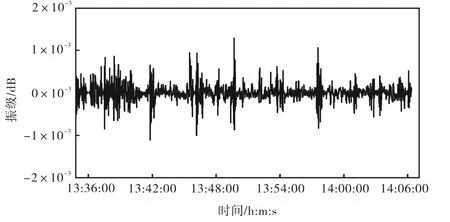
图3 工作日地铁振级神经网络拟合误差曲线

图4 19日13：34-13：49振级为样本的网络预测误差

图5为19日13：34-13：49的振级测试样本与预测输出对比曲线．图6反映了以19日17：00-17：15的振级作为测试样本网络的测试误差曲线，可以发现：图6所用的测试样本和该网络的训练样本并不在同一时段，由于地铁运营周期及规律相同，因此并没有影响网络预测性能，网络预测绝对误差最大为0.16,dB．

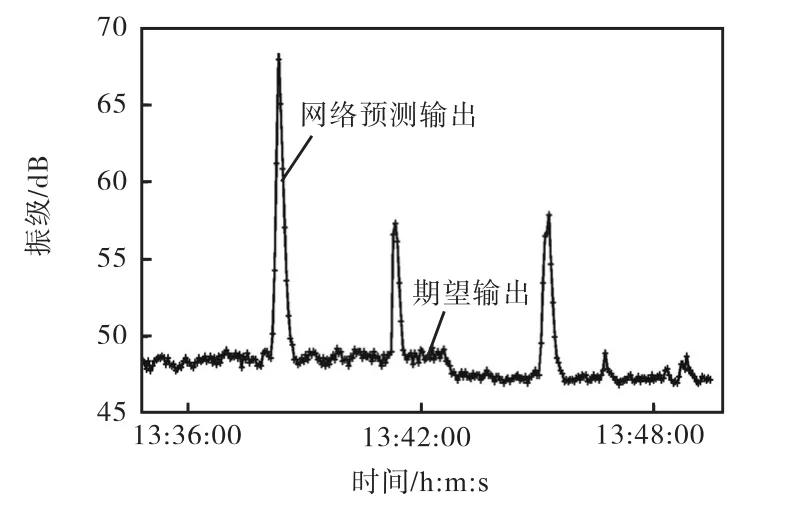
图5 19日13：34-13：49振级测试样本与网络预测输出

图7反映了20日13：34-13：54时段的振级作为测试样本下网络的测试误差曲线，该测试样本与该网络的训练样本属同一时段，但由图7可见，网络预测误差很大，最大绝对误差达20,dB．原因是20日为周六，地铁运行时间与工作日的有所不同，因此该RBF神经网络模型无法反映周末的地铁运行规律．

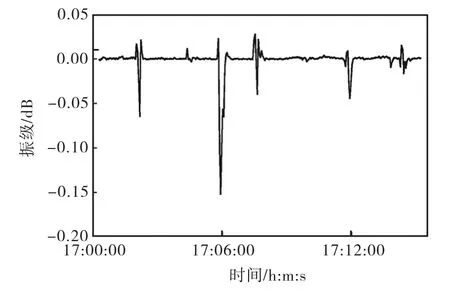
图6 19日17：00-17：15振级为样本的网络预测误差

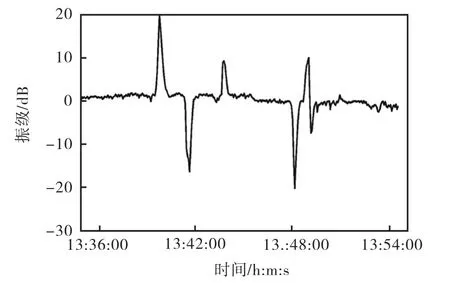
图7 20日13：34-13：54振级为样本的网络预测误差

图8显示了19日13：34-13：49时段的数据做测试样本下的峰值对比，图9则显示了19日17：00-17：15时段振级为测试样本下的峰值对比．图8中出现峰值的时刻为13：38：20,左右，实测峰值为68.3,dB，预测峰值为67.96,dB，绝对误差为0.34,dB；图9出现峰值的时刻为17：05：56左右，实测峰值为66.1,dB，预测峰值为65.95,dB，绝对误差为0.15,dB．

通过对比可见，网络预测峰值出现的时刻与实测峰值出现的时刻相同，峰值大小近似相等．峰值预测结果表明，在测试点50,Hz频率下的地铁振动并没有达到振动标准里规定的振级限值昼间70,dB，因此建筑物内人可以感觉到振动，但并没有达到无法忍受的程度，不会对其生活造成太大影响．

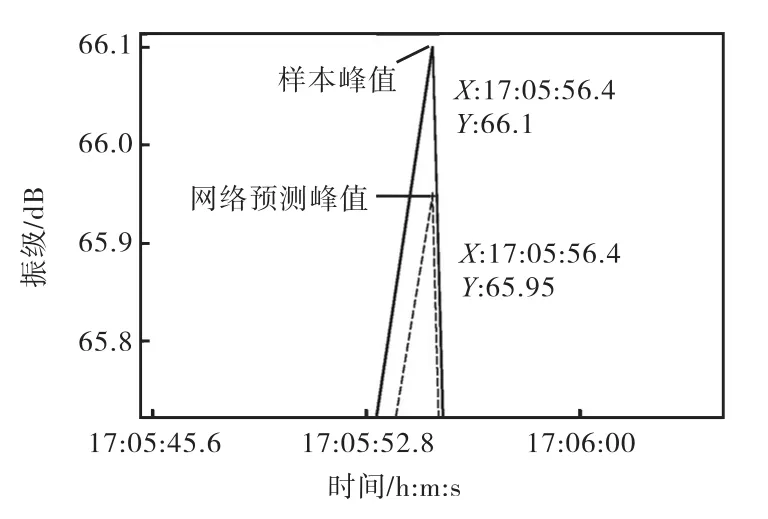
图9 19日17：00-17：15振级为测试样本的振级峰值对比

3.2 双休日地铁振级的RBF神经网络模型构建与测试

选取2014-09-20T 8：00-9：00的数据进行网络模型的构建，拟合双休日地铁振级曲线．选取2014-09-21T 8：00-8：15和9：30-9：45两个时段的数据分别测试模型的预测性能．表3-4给出了神经网络训练过程中设定的相关参数和网络训练完成后的相关权值及阈值．分析曲线如图10-12所示．

表3 神经网络训练参数

表4 神经网络训练后权值与阈值

图10为拟合误差曲线，误差范围在±1×10-3,dB之间，可见拟合效果很好．将该网络应用到振级预测中，对2014-09-21T 9：30-09：45时段的振级进行了预测，并与实测数据进行对比，测试误差曲线见图11，预测绝对误差最大为0.03,dB．

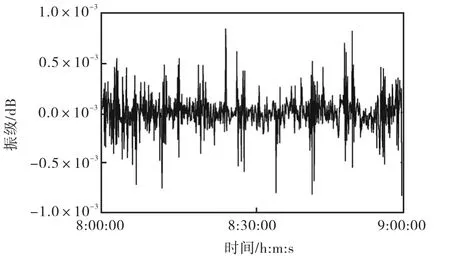
图10 双休日地铁振级神经网络拟合误差曲线

图12显示了21日9：30-9：45振级为测试样本下的峰值对比．由图12可知，出现峰值的时刻为9：33：3.96，实测峰值为66.00,dB，预测峰值为65.97,dB，可见预测峰值与实测峰值出现的时刻相同，且也并未达到规定的限值70,dB．

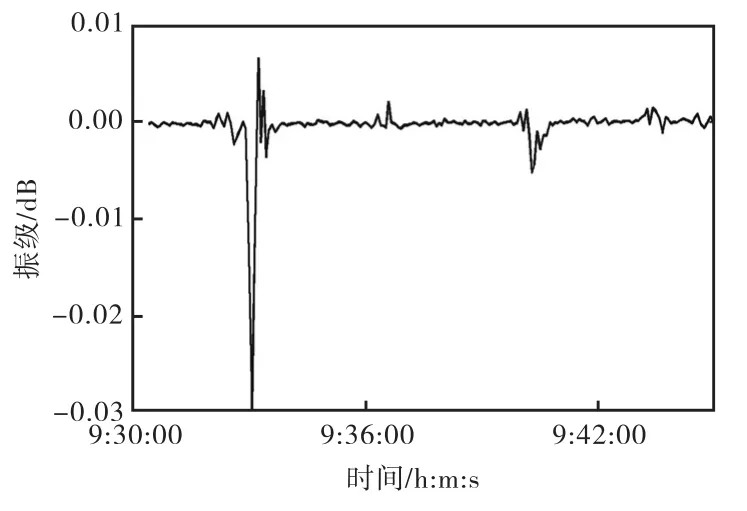
图11 21日9：30-9：45振级为样本的网络预测误差

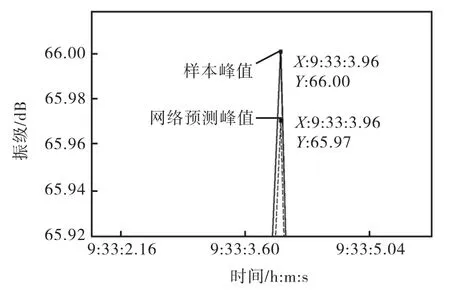
图12 21日9：30-9：45振级为测试样本峰值对比

4 结 语

结合滑动窗口技术，选取实测的地铁振动的振级数据作为训练样本和测试样本，构建了RBF神经网络模型．利用RBF神经网络的自学习和非线性映射能力，很好地实现了对工作日和双休日地铁振动振级曲线的拟合和峰值预测，同时表明该线路的地铁振级峰值并未达到限值，对周边的居民生活并不会造成太大的影响．

由于影响振动的因素众多，通过对既有地铁线路进行有目的性的大量测试，实现数据库积累，并以此为基础，建立振动预测模型，这对工程实践尤为重要．

通过建立预测模型，不但可以充分掌握地铁振动的规律，分析地铁振动对周围环境及居民生活的影响，对已有的减振预测措施进行总结和再认知，同时也是指导新线正确设计的有效手段，便于相关工程部门采取有效的减振措施和管理措施，降低因地铁振动对居民生活舒适度的影响．

［1］ 郑 薇. 列车经过对周边建筑的振动影响分析[D]. 杭州：浙江大学，2006：39-55.

［2］ 丁洁民，尹志刚. 地铁引起建筑物振动舒适度分析[J]. 振动与冲击，2008，27(9)：96-99.

［3］ 张晓春，张辰辰，张 磊，等. 地铁列车振动对临近建筑内人体舒适度的影响研究[J]. 中国矿业大学学报，2009，38(6)：835-839.

［4］ 何浩祥，闫维明，张爱林，等. 竖向环境振动下人与结构相互作用及舒适度研究[J]. 振动工程学报，2008，21(5)：446-451.

［5］ 蒋 通，李丽琴，刘 峰. 地铁引起邻近建筑物楼板的振动及简易预测方法[J]. 结构工程师，2012，28(6)：29-33.

［6］ TAKEMIYA H. Simulation of track-ground vibrations due to a high-speed train：the case of X-2000 at Ledsgard[J]. Journal of Sound and Vibration，2003，261(3)：503-526.

［7］ 辜小安，刘先章，张春华. 地铁环境振动预测方法浅析[J]. 环境工程，1996，14(5)：35-39.

［8］ 宝音贺喜格，黄文虎，姜兴渭. 神经网络在轨道动力学中的应用[J]. 振动与冲击，1999，18(3)：67-70.

［9］ 韦艳玲. 一种改进的RBF神经网络在预测虫害中的应用研究[J]. 科学技术与工程，2013，13(1)：136-139.

［10］ 孟 杰，吕正兵. RBF神经网络在道路交通事故预测中的应用[J]. 常熟理工学院学报(自然科学版)，2012，26(2)：86-90.

［11］ 中华人民共和国环境保护部，国家质量监督检验检疫总局. 城市区域环境振动标准：GB 10070—1988[S].北京：中国标准出版社，1988：1-4．

［12］ 周 博，宇善良，徐连双. 地铁运行振动规律及减振措施[J]. 辽宁师范大学学报(自然科学版)，2010，33(2)：172-174.

［13］ 雷绍兰，孙才新，周 湶，等. 基于径向基神经网络和自适应神经模糊系统的电力短期负荷预测方法[J].中国电机工程学报，2005，25(6)：78-82.

［14］ 李 蔚，盛德仁，陈坚红，等. 双重BP神经网络组合模型在实时数据预测中的应用[J]. 中国电机工程学报，2007，27(17)：94-97.

［15］ 沈 强，陈从新，汪 稔. 边坡位移预测的RBF神经网络方法[J]. 岩石力学与工程学报，2006，25(1)：2,882-2,887.

The Subway Vibration Forecast Analysis Based on RBF Neural Network

WANG Xiulia，PAN Leia，PENG Guilia，LIANG Yinb，WANG Beibeia
(a. School of Control and Mechanical Engineering；b. School of Energy and Safety Engineering，TCU，Tianjin 300384，China)

Along with the development of city rail transport，the influence of the vibration and noise caused by train movement are bigger and bigger on the environment and people’s life. How to forecast the vibration accurately and analyze its propagation rule effectively are very important. It also can present some valuable reference data to depress vibration and noise. The measured data of the vibration level is combined effect of all factors which cause the subway vibration，implying the rule of the subway vibration. Using the measured data of the vibration level as sample，radial basis function (RBF) neural network forecasting model is structured with combinations of the sliding window technology. At last the fitted curves are obtained and the vibration’s peak value forecast is realized. Some examples illustrate that the forecasting result is good and the forecast model fully reflects the mapping relation of nonlinear function about the subway vibration system.

subway vibration；acceleration vibration level；forecast；radial basis function neural network

TP183；U231

A

2095-719X(2016)06-0465-06

2015-10-30；

2016-03-30

天津市高等学校科技发展基金计划项目(20140527)

王秀丽（1977—），女，天津人，天津城建大学讲师，硕士．