装备保障资源均衡遗传算法优化与仿真

王建成， 邱 辉， 郭 凯

(1. 装备学院 装备指挥系, 北京 101416； 2.装备学院 研究生管理大队, 北京 101416； 3.61046部队)



装备保障资源均衡遗传算法优化与仿真

王建成1， 邱 辉2, 3， 郭 凯1

(1. 装备学院 装备指挥系, 北京 101416； 2.装备学院 研究生管理大队, 北京 101416； 3.61046部队)

合理利用装备保障资源是组织装备保障活动的必然要求，科学规划是装备保障资源合理利用的基本前提。装备保障任务工期内对保障资源需求的波动量越小越有利于装备保障活动的高效组织、实施、管理以及装备保障效能的提高。资源均衡优化是实现资源需求均衡的重要技术手段。传统求解资源均衡问题的精确解法和启发式优化方法在解决这类中大规模问题时难以奏效，带修复算子的遗传算法能够在一定程度上克服这些算法存在的缺点，其有效性通过获得几个模拟问题的最优或次最优解得以验证。

资源均衡；装备保障；遗传算法；网络计划

装备保障资源是装备保障活动的重要物质基础，装备保障活动对保障资源需求的波动量越小越有利于装备保障活动的组织、实施、管理以及装备保障效能的提高。资源均衡优化是实现资源需求均衡的重要技术途径[1]和进行装备保障任务规划计划的重要环节，其目标是通过合理安排各道工序，从而尽可能地减少任务工期内对资源使用需求的波动。由于资源均衡优化是NP(Non-deterministic Polynomial)问题，用完全枚举法求解中规模资源均衡问题时因搜索空间过大而难以获得问题的最优解。传统求解这类问题的数学模型包括整数规划、动态规划和分支定界法等[2-5]，但均因无法有效解决组合爆炸瓶颈问题而仅能用于求解小规模问题。近年来，遗传算法(Genetic Algorithms，GA)作为一个全局随机搜索算法[6-8]，具备有效克服组合爆炸问题的能力，因而被用来求解装备保障资源优化问题，从而在一定的折中条件下获得中大规模资源均衡优化问题较为满意的规划解。

1 问题描述

装备保障资源均衡优化问题可以用网络图描述。图1所示为一项装备保障任务的双代号网络，其中有9道工序和6个节点。工序之间具有确定的前导后继关系，并且每一对节点间的工序数不超过1。(i,j)表示节点i和j之间的一道工序，例如(4, 5)表示工序“G”。所有工序的集合记为W，所有虚工序的集合记为V，工序(i,j)的所有紧前工序的集合记为P(i,j)。

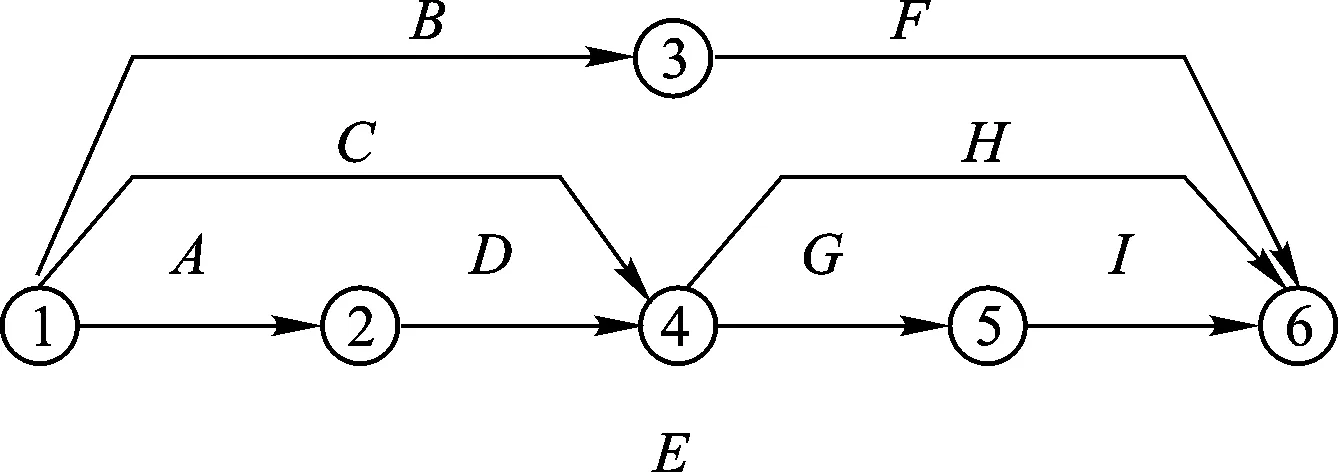
图1 装备保障任务双代号网络

(1)

(2)

2 带修复算子的遗传算法

遗传算法实际上是通过对决策变量的迭代操作实现的。为获得GA解，首先必须精心设计染色体结构。一条染色体由N个基因组成，每一个基因对应一个决策变量，表示一道工序的计划开工时间。简单遗传算法的遗传算子由选择、交叉和变异算子构成。选择、交叉和变异算子分别选用赌轮选择、单点交叉和随机变异。由于遗传算子的作用，一条可行的染色体可能退变为非可行的染色体，即非可行解。如果这种情况发生，就要使用修复算子对工序(i,j)的实际开工时间tAS(i,j)进行修复。迭代过程中利用修复准则对一条染色体进行适时检查，当发现该染色体中某一工序在其所有紧前工序还未结束时开工，即当式(3)所给出的不等式成立时，就表示该染色体为非可行染色体，就应该启动修复算子进行染色体修复。修复算子强制非法基因值等于工序(i,j)所有紧前工序实际完成时间的最大值。

(3)

遗传算法是通过不断产生新的个体、更新当前最优染色体来求解最优化问题的。进化过程中，解的质量由适应度函数进行评价，并且这种评价是染色体选择的前提。对于工期固定资源规划问题，工期内资源需求量波动越小，染色体的适应性越强。因此，定义目标函数g(tAS)如式(4)：

(4)

适应度函数f(tAS)可以分别用相对适应度函数和绝对适应度函数定义，分别如式(5)和式(6)所示。

(5)

(6)

3 仿真结果

利用带修复算子的遗传算法求解了2个仿真算例：一个小规模问题和一个中规模问题。算法用Matlab语言实现。

3.1 小规模问题

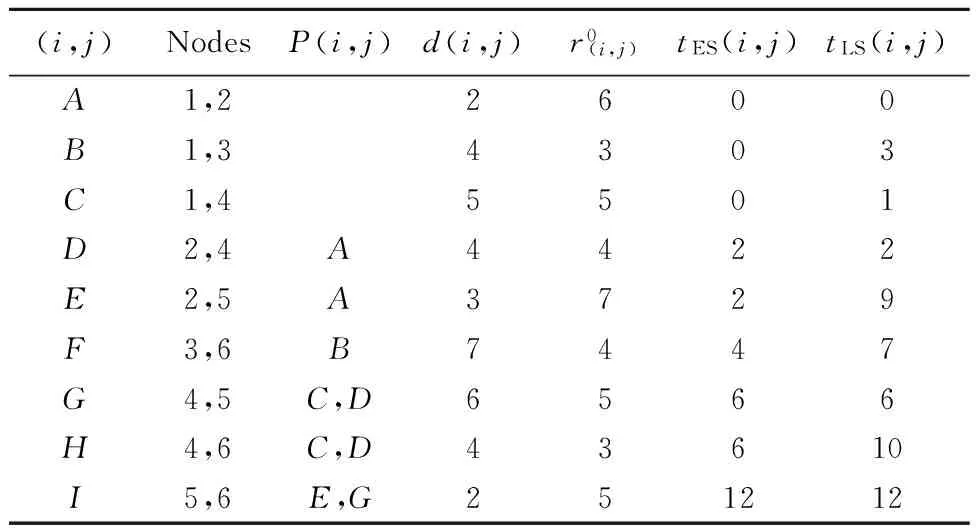
表1 小规模问题参数及CPM结果

精确解。对于该小规模问题，可利用完全枚举法给出问题的精确解。取所有关键工序的实际开工时间为tES(i, j)，将所有非关键工序的实际开工时间在区间[tES(i,j) tLS(i, j)]遍历取值。求解时需要搜索的解的总数为1 280，其中非可行解的个数为480，可行解的个数为800。对这些可行解，通过比较其所对应的任务工期内资源需求量方差的大小选择出最优解。其中最好的前10个精确解如表2所示。对于最优目标值2.863 7，存在有6个最优解，如表2的前6行所示。对这种最优解不唯一的优化问题，传统的优化方法很难奏效。

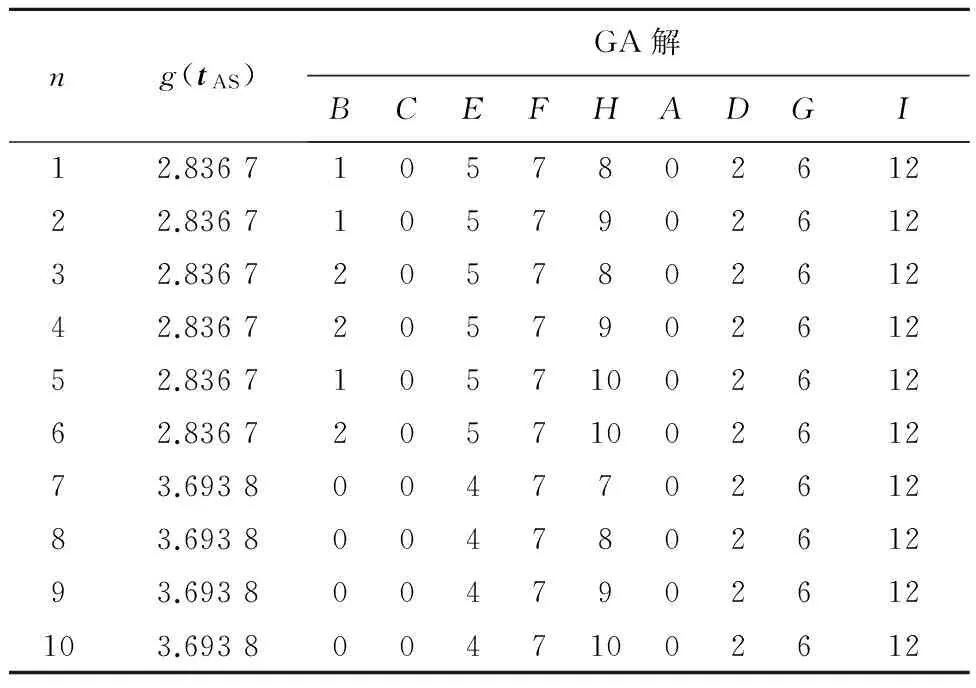
表2 小规模问题前10个最优精确解

GA解。参数popSize=20，chromLen=9，PC=0.65，PM=[0.35 0.25]，maxGen=10。采用相对适应度函数。运行进化程序10次，所得到的GA解列于表3。与精确解对比发现，遗传算法得到的解中有9个与表2中的最优解一致，这充分表明遗传算法求解资源均衡优化问题时解的质量。从表3给出的GA解可见，当目标值g(tAS)相同时，遗传算法可以得到不同的染色体，这充分显示出遗传算法在优化这类多极值目标函数时具有随机收敛到多个全局最优解的优越性能。目标值的进化曲线如图2所示。显而易见，当问题的规模较小时，进化过程迅速向精确解收敛。

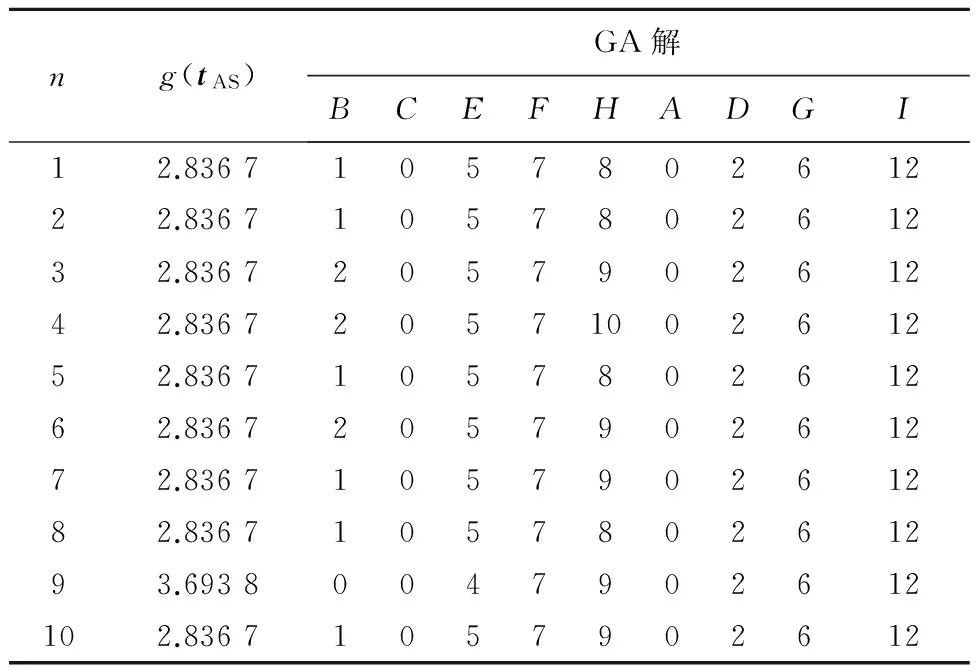
表3 小规模问题10次运行GA解

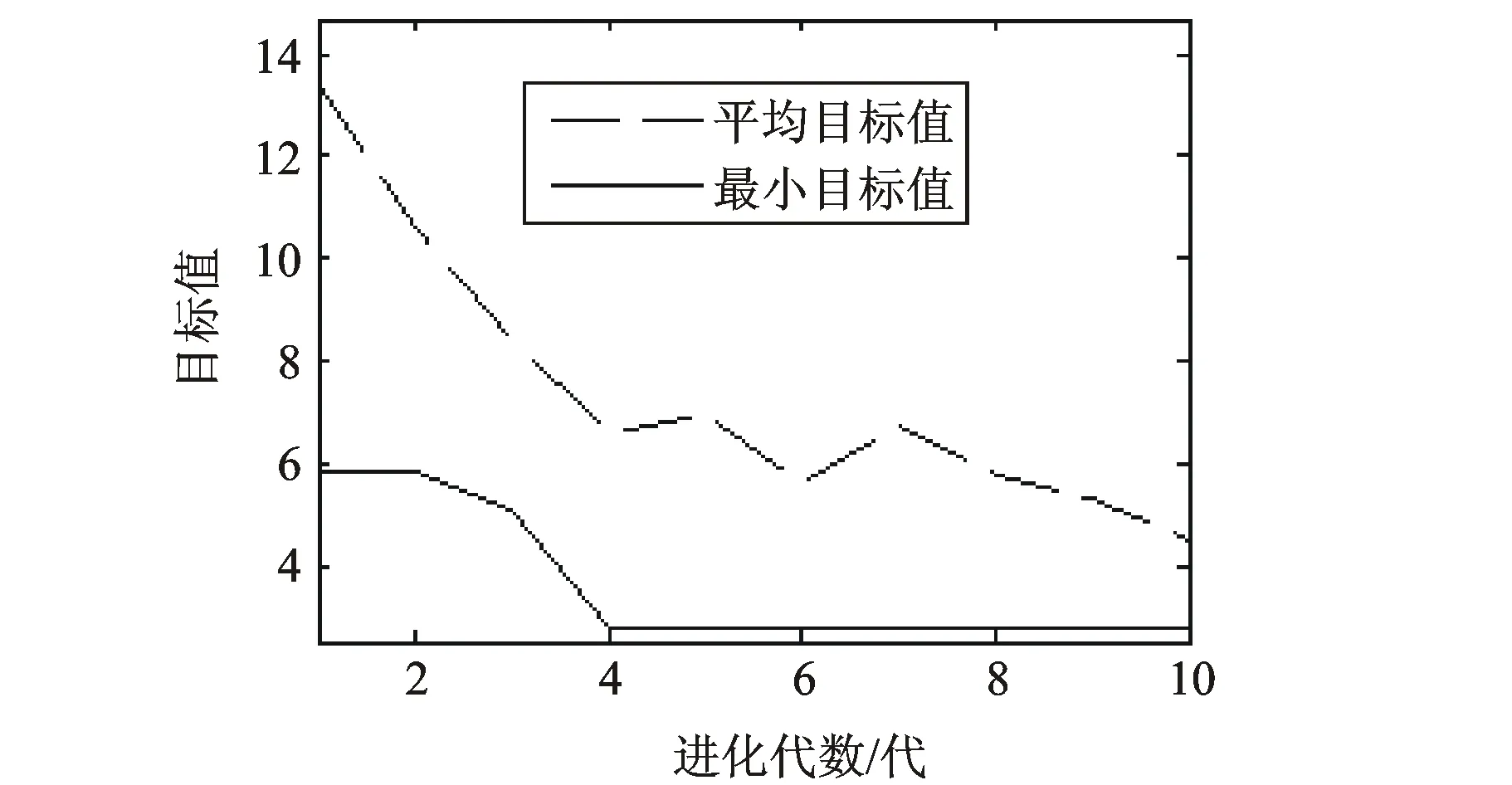
图2 目标值进化曲线

3.2 中规模问题

图3 包括17道实工序和12个节点的装备保障任务等效双代号网络

表4 中规模问题参数及CPM结果

图4 中规模问题各工序规划的实际开工时间

图5 中规模问题工期内单位时间资源需求量

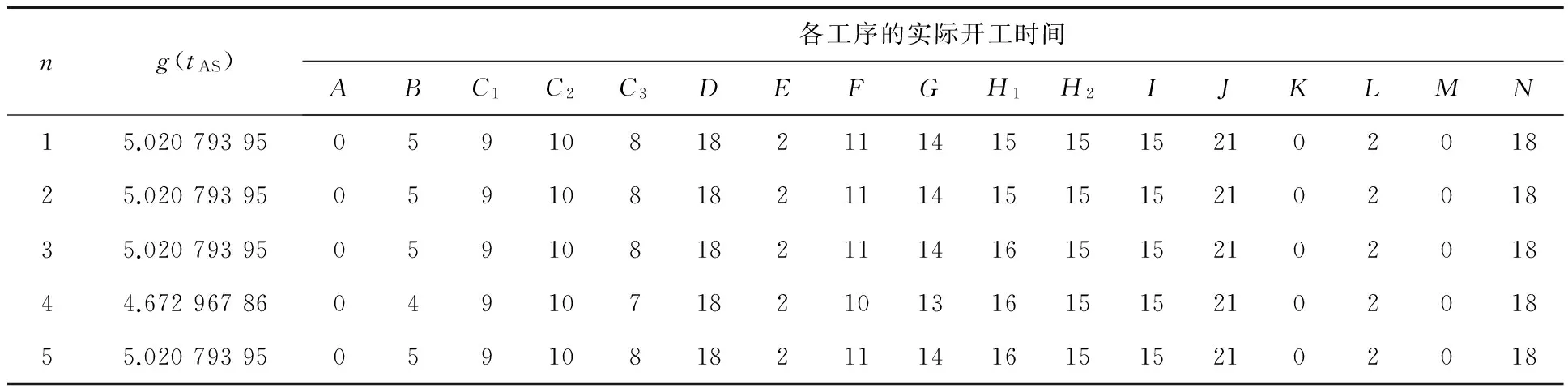
ng(tAS)各工序的实际开工时间ABC1C2C3DEFGH1H2IJKLMN15.020793950591081821114151515210201825.020793950591081821114151515210201835.020793950591081821114161515210201844.672967860491071821013161515210201855.0207939505910818211141615152102018

4 结 束 语

本文研究了基于遗传算法的中小规模可更新装备保障资源优化问题，设计了用于修复非可行染色体的修复算子，并通过仿真算例验证了该方法的有效性。对于中大规模特别是大规模问题的求解以及实现初始种群的多样性方面，仍需进一步探索。该方法不仅可用于装备保障活动的规划计划，对于其他工作中涉及的同类型资源优化问题具有普遍的适用性。

References)

[1]欧阳红祥，刘炳胜，李欣.网络计划多资源均衡优化遗传算法[J].武汉理工大学学报(信息与管理工程版)，2013，35(2):180-182.

[2]左传友.PERT方法优化的导弹技术准备流程[J].海军航空工程学院学报，2008，23(5):569-572.

[3]LEU S S，YANG C H，HUANG J C.Resource leveling in construction by genetic algorithm-based optimization and its decision support system application [J].Automation in Construction，2000，10(1):27-41.

[4]RIECK J，ZIMMERMANN J，GATHER T.Mixed-integer linear programming for resource leveling problems [J].European Journal of Operational Research，2012，221(1):27-37.

[5]马登武，郭小威，吕晓峰.基于网络计划技术的舰载机航空导弹转运流程[J].兵工自动化，2010，29(9):48-51.

[6]AHMED B S，NEIL N E.Use of genetic algorithms in resource scheduling of construction projects [J].Journal of Construction Engineering and Management，2004，130(6):869-877.

[7]HEGAZY T.Optimization of resource allocation and leveling using genetic algorithms[J].Journal of Construction Engineering Management，1999，117(3):380-392.

[8]瞿军，吴文军，黄全.导弹技术保障资源均衡优化的遗传算法求解[J].海军航空工程学院学报，2010，25(2):137-140.

(编辑：李江涛)

Optimization and Simulation of Genetic Algorithm for Equipment Support Resource Equilibrium

WANG Jiancheng1， QIU Hui2,3， GUO Kai1

(1. Department of Equipment Command, Equipment Academy, Beijing 101416, China；2. Department of Graduate Management, Equipment Academy, Beijing 101416, China； 3. 61046 Troops, China)

Reasonable utilization of equipment support resources is necessary when performing equipment support activities and scientific planning is the basic premise for reasonable utilization of the equipment support resource. In the implementation period of equipment support task, the smaller the fluctuation of the support resource demand is, the better the organization, implementation and management of equipment support activities is and this will improve equipment support effectiveness. Resource equilibrium and optimization are key technical approaches to the equilibrium of resource demand. However, traditional precise method and heuristic optimization method are inapplicable to such problems at a mid/large scale. Fortunately, the genetic algorithm with reparative factor can overcome the shortcoming of above algorithms and may be verified in terms of effectiveness by obtaining the optimal or suboptimal solution to several problems of modeling.

resource equilibrium; equipment support; genetic algorithm; network planning

2016-03-02

王建成(1970-)，男，副教授，主要研究方向为装备保障与指挥。wjianch@sohu.com

E91

2095-3828(2016)06-0133-04

A DOI 10.3783/j.issn.2095-3828.2016.06.025