线性离散系统非脆弱H∞状态反馈控制器设计

张 亮 ，李 明，李树多

(渤海大学 工学院，辽宁 锦州 121013； 鞍山师范学院 教育科学与技术学院, 辽宁 鞍山 114005)



线性离散系统非脆弱H∞状态反馈控制器设计

张 亮*，1，李 明1，李树多2

(渤海大学 工学院，辽宁 锦州 121013； 鞍山师范学院 教育科学与技术学院, 辽宁 鞍山 114005)

研究了线性离散时间系统非脆弱H∞状态反馈控制问题. 我们的主要目的是针对线性离散时间系统设计非脆弱H∞状态反馈控制器使得闭环控制系统在控制器存在参数变化或存在不确定性时仍然能保证系统渐渐稳定并满足给定的H∞性能指标. 具体是通过利用Lyapunov函数法并且考虑一个新的控制律, 给出了基于LMI非脆弱状态反馈控制器存在的充分条件.

线性离散系统；非脆弱；状态反馈H∞控制器；线性矩阵不等式

0 引言

H∞控制因在处理非结构式不确定系统方面的优势，在过去的二十多年间受到了广泛的关注，并成功的应用于机器人、航空航天、电力系统等多个领域〔1-3〕. 另一方面，文献〔4〕指出如果闭环系统的某些特性，特别是稳定性，对控制器参数的变化或不确定性非常敏感，则这样的控制器可被称之为脆弱的(fragile)/无弹性的(non-resilient)〔5〕通过例子表明传统的最优和鲁棒控制器设计方法，所设计出来的控制器都可能具有脆弱性，即控制器的参数发生微小的偏移，将导致闭环系统的稳定性被破坏和/或性能下降，对于非脆弱控制的研究近年来引起广大学者的广泛关注，参见文献〔6-7〕. 同时考虑系统不H∞指标和非脆弱控制研究参见文献〔8-12〕.

本文在已有文献的基础上，提出一种新的非脆弱H∞状态反馈控制器的设计方法，通过一个新的控制律及参数依赖Lyapunov得到一个新的控制器的LMIs设计条件，是其不仅具有非脆弱性而且同时满足H∞性能指标，通过Matlab中LMI工具箱可以很方便的求得.

1 问题描述

考虑如下状态空间描述的线性离散系统方程：

(1)

其中，x(k)∈Rn，u(k)∈Rm，z(k)∈Rv，w(k)∈Rv分别为系统的状态变量，系统输出变量，受控输出变量和扰动变量；A∈Rn×n，B∈Rn×m，E∈Rn×v，C∈Rq×n，D∈Rq×m，F∈Rq×v，为适当维数的系数矩阵.

考虑如下带有加性增益的非脆弱状态反馈控制律：

u(k)=(K+ΔK)G-1x(k)

(2)

其中，ΔK=MkFkNkFkTFk≤I.

由此可得闭环系统如下：

(3)

同时我们注意到

(4)

本文的目的是设计控制器(2)，使得下述两个条件成立：

(1)当w(k)=0时，闭环系统(3)是渐进稳定的；

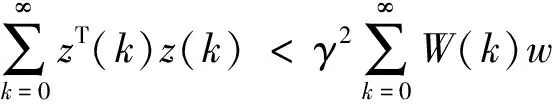
下面引理将会在后面的推导中用到

引理1:〔10〕对于给定矩阵ΓΛ，和对称矩阵Φ，对于FTF

Φ+ΓFΛ+ΛTFTΓT<0

成立，只要存在一个恒定的标量ε>0满足：

Φ+ε-1ΓΓ+εΛTΛ<0

2 结果与讨论

定理1：考虑闭环系统(3)，对于给定标量λ和γ>0，如果存在矩阵P>0，G，K，Mk和Nk使得下面矩阵不等式成立：

(5)

那么闭环系统(3)渐进稳定且H∞控制性能指标γ>0能够保证，同时控制器具有非脆弱性.

证明：定义如下Lyapunov函数

V(x(k))=xT(k)G-TPG-1x(k)

(6)

从(3)，(4)，(6)可得

ΔV(x(k))+zT(k)z(k)-γ2wT(k)w(k)=

xT(k+1)G-TPG-1x(k+1)-xT(k)G-TPG-1x(k)+[(C+D(K+ΔK)G-1)x(k)+

(7)

Fw(k)]T×[(C+D(K+ΔK)G-1x(k)+Fw(k)]-γ2wT(k)w(k)+He{[x(k+1)-

(A+B(K+ΔK)G-1x(k)-Ew(k)]×[xT(k)G-T+λxT(k+1)G-T]}=ζT(k)Ξζ(k)

其中ζ(k)=[xT(k) wT(k) xT(k+1)]，

(8)

Π33=He{λG-T}+G-TPG-1

当，Ξ<0我们很容易证明w(k)=0时系统渐进稳定，若要ΔV(x(k))+zT(k)z(k)-γ2wT(k)w(k)<0，那么只要Ξ<0，对上式应用Schur补得Ξ<0等价于Ω<0

(9)

成立，其中

Ω33=He{λG-T}+G-TPG-1

左乘diag(GT,I,GT,I)右乘diag(G,I,G,I)，我们有上式等价于

(10)

上式可以写成

(11)

通过引理1得上式等价于(12)：

(12)

对(12)应用引理1并Schur补，再调用diag(I,I,I,I,I,εI)执行同余变换我们可以得到(5).

3 结论

本文研究了线性离散时间系统的非脆弱H∞状态反馈控制问题，通过考虑新的控制律同时利用Lyapunov稳定理论给出基于线性矩阵不等式(LMI)线性离散时间系统非脆弱H∞状态反馈控制器设计的充分条件，使得在控制器参数发生变化或存在不确定时仍然能够保证闭环控制系统渐进稳定并具有给定的H∞性能指标.本文仅考虑了控制器具有加性增益的情况，未来我们将进一步研究具有乘性增益的非脆弱H∞状态反馈控制问题.

〔1〕CHANG X H. Robust output feedback H-infinity control and filtering for uncertain linear systems〔M〕. Springer Science & Business, 2014.

〔2〕HUANG C, BAI Y, LIU X. H-infinity state feedback control for a class of networked cascade control systems with uncertain delay〔J〕. IEEE Transactions on Industrial Informatics, 2010, 6(1): 62-72.

〔3〕CHANG X H.H∞ controller design for linear systems with time-invariant uncertainties〔J〕. International Journal of Control, Automation and Systems, 2011, 9(2): 1-5.

〔4〕KEEL L H. Bhataeharyya S P. Robust, fragile, or optimal?〔J〕. IEEE Transactions on Automatic Control, 1997, 42(8): 1098一1105.

〔5〕CHE W W, YANG G H, JIN X Z. Sparse structured non-fragileH∞ controller design for linear systems〔J〕. International Journal of Control, Automation and Systems, 2013, 11(4): 704-710.

〔6〕WANG C, SHEN Y. Delay-dependent non-fragile robust stabilization andH∞ control of uncertain stochastic systems with time-varying delay and nonlinearity〔J〕. Journal of the Franklin Institute, 2011, 348(8): 2174-2190.

〔7〕KAO Y, XIE J, WANG C, et al. A sliding mode approach toH∞ non-fragile observer-based control design for uncertain markovian neutral-type stochastic systems〔J〕. Automatica, 2015, 52: 218-226.

〔8〕CHE W W, YANG G H. Non-fragile dynamic output feedbackH∞ control for discrete-time systems with FWL consideration〔J〕. International Journal of Control, Automation and Systems, 2011, 9(5): 993-997.

〔9〕WANG Z, DING D, SHU H. Non-fragileH∞ control with randomly occurring gain variations, distributed delays and channel fadings〔J〕. IET Control Theory & Applications, 2014, 9(2): 222-231.

〔10〕PETERSEN I R. A stabilization algorithm for a class of uncertain linear systems〔J〕. System & Control Letters, 1987, 8(4):351-357.

〔11〕HU Q L. Sliding mode maneuvering control and active vibration damping of three-axis stabilized flexible spacecraft with actuator dynamics〔J〕.Nonlinear Dynamics, 2008, 52(3): 227-248.

〔12〕PUJOL G. ReliableH∞ control of a class of uncertain interconnected systems: an LMI approach〔J〕. International Journal of Systems Science, 2009, 40(3): 649-657.

〔13〕汪锐, 冯佳昕, 赵军. 一类线性不确定切换系统的非脆弱控制器设计方法〔J〕. 控制与决策, 2006, 21(7): 735-738.

No fragile state feedbackH∞ controller design for linear discrete -time systems

ZHANG Liang1，LI Ming1, LI Shu-duo2

(College of engineering, Bohai University, Jinzhou 121013, China； School of Education science and Technology, Anshan Normal University , Anshan 114005, China)

This paper considers the problem of no fragile state feedbackH∞ control for liner discrete-time system. Attention is focused on the design of a no fragile state feedbackH∞ controller to mitigate the effect of controller parameters variation such that the close-loop control system is asymptotically stable with a prescribedH∞ performance. By using Lyapunov function approach and a new control law, a sufficient condition is presented in terms of linear matrix inequalities (LMIs) for such no fragileH∞ state feedback controller exists.

discrete-time system; no fragile;H∞ state feedback controller; LMIs

2016-04-08.

国家自然科学基金项目(No:61104071)；辽宁省高等学校杰出青年成长计划项目(No:LJQ2012095)；辽宁省装备制造综合自动化重点实验室开放项目(No:1120211415).

张亮(1987-)，男，助理实验师，主要从事自动化系统控制理论方面的研究.

md18638@126.com.

TP

A

1673-0569(2016)04-0361-04