铁路不固定区段旅客列车车底套用优化研究
崔姗姗
(西南交通大学交通运输与物流学院,四川成都 610031)
铁路不固定区段旅客列车车底套用优化研究
崔姗姗
(西南交通大学交通运输与物流学院,四川成都 610031)
分析当前旅客列车车底的运用方式,提出铁路实行车底套用可以提高车底运用效率,并且可以减少车底接续时间。通过构建车次连接网络图,对初始可行车次连接任务串进行搜索,以每个车次都能被覆盖且仅被覆盖一次为约束条件,以车底使用数量最少为目标函数,建立不固定区段的车底套用模型,并采用遗传算法进行求解。结合北京、武汉、广州、上海4个地区一些大型客运站旅客列车的运行情况对模型加以运用,结果表明:车底的实际接续时间减少,减少了车底的使用数量。
旅客列车;不固定区段;车底套用;遗传算法
车底套用是指两个或两个以上的旅客列车使用同一车底。不固定区段列车车底套用是指在假定各车底之间没有差别的情况下,车底完成一次列车任务后,下一次担当列车的运行区段没有限制,一组车底多车次套用。这种模式可以压缩车底不必要的在站停留时间,提高客车使用效率,也可以节约铁路运营成本,提高铁路运营效益。文献[1-2]使用大小交路嵌套的模式对城市轨道交通的车体运用进行研究;文献[3-8]对单车种单基地条件下的动车组运用进行优化;文献[9-15]基于既定详图对旅客列车车底套用进行优化研究;文献[16-17]采用模拟退火算法对车底套用模型进行求解;文献[18-20]对机组航班任务串编排的限制条件及优化目标进行了深入研究。
本文借鉴航空公司机组航班任务串进行机组排班的方法,建立不固定区段铁路旅客列车车底套用优化模型,并通过实例对模型进行验证。突破车底配属制,以期提高车底运用效率,减少车底接续时间,从而减少车底使用数量。
1 我国铁路旅客列车车底运用方式分析
1.1 固定区段运用方式
1.1.1 特点
我国铁路旅客列车采用固定配属和固定运用区段的方式,这种方式有利于运输组织,但不利于提高车底运用效率,不能减少车底使用数量,主要表现在:
1)客车车底在站停留时间过长
“朝发夕至”和“夕发朝至”类型列车大量开行,导致客车车底在站停留时间过长,这种类型的列车多集中于路网干线上的大型中心客运站。
2)客运设备使用和人员安排等问题
客运站列车到发高峰期时,会出现到发线、客车车库和客车整备所的存车线、整备设备以及设备的配置等运用紧张的问题,而当车站的到发列车数量很少时,又会出现设备闲置的情况,使设备的利用率降低。对于车辆乘务组,需要随车作业,如果采用包乘制,对于“朝发夕至”和“夕发朝至”的列车乘务组来说,车底在折返站和配属站的停留时间较长,则在作业时间的安排上会出现一定困难。
1.1.2 列车运行
以临沂-北京、北京-秦皇岛段的列车运行为例。
1)临沂-北京区段
该区段列车运行情况如图1所示。第一列列车在第1天的16:08从临沂站出发,经运行线①于第2天05:00到达北京站,在北京站停留后,于23:26从北京站出发,经运行线③于第3天12:12到达临沂站,在临沂站停留后,继续重复之前的运行过程。在此过程中,第2天的16:08需要从临沂站再发一列车开往北京,由于第一列列车还在执行任务没有回到临沂站,需要指派另一列列车在第2天的16:08经运行线②运行到北京。在第3天16:08第1组车底已经回到临沂站,可以继续执行任务。因此,临沂-北京段需要2组(将一定数量的车底(车厢)编成1列,即1组)车底。
2)北京-秦皇岛区段
该区段的列车运行情况如图2所示。列车在第1天10:52从北京出发,经运行线①在当天13:48到达秦皇岛站,在秦皇岛停留后,当天16:35经运行线②于20:41回到北京站,在北京站停留后,于第2天10:52经运行线③继续开往秦皇岛。即从北京站到秦皇岛站需要1组车底。
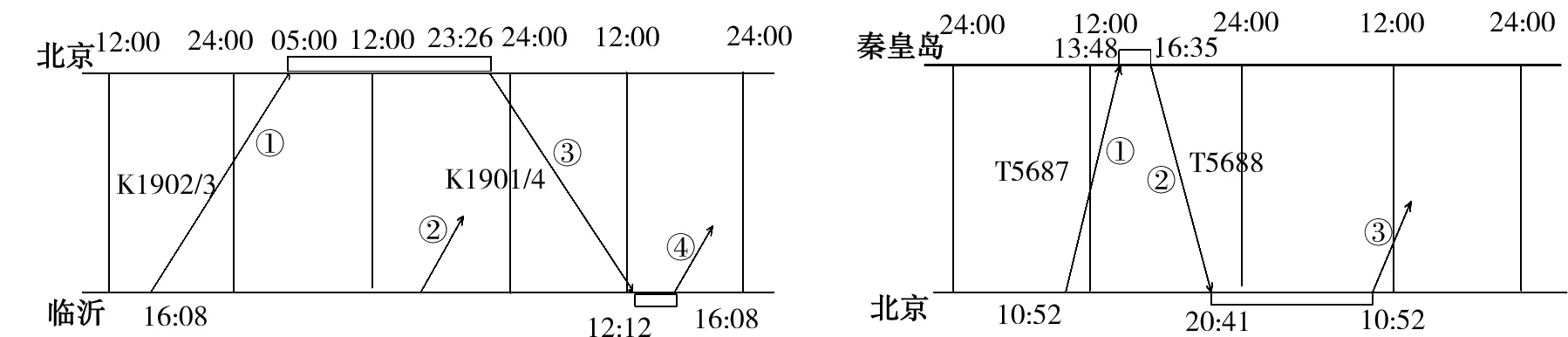
图1 临沂-北京区段列车周转 图2 北京-秦皇岛区段列车周转
1.2 不固定区段运用方式
1.2.1 特点
通过不固定区段旅客列车车底套用的方法将车底的空余时间利用起来,使就近的列车有效接续,减少旅客列车在站停留时间,节省车底使用数量。
1.2.2 列车运行
当将临沂-北京、北京-秦皇岛这2个区段列车车底套用时,如图3所示。列车第1天16:08从临沂出发,经运行线①于第2天05:00到达北京站,在北京站停留后,于第2天的10:52经运行线②13:48运行到达秦皇岛,在秦皇岛停留后,于第2天16:33从秦皇岛出发,经运行线③回到北京站,再于第2天23:36经运行线⑤于第3天12:08回到临沂站,然后在第3天16:08从临沂出发,重复之前的运行过程。在此过程中,第2天还需另外一组列车于16:08从临沂出发沿运行线④至北京站,重复前一列车的运行过程。整个运行过程需要2组车底,比原来节省了1组车底。
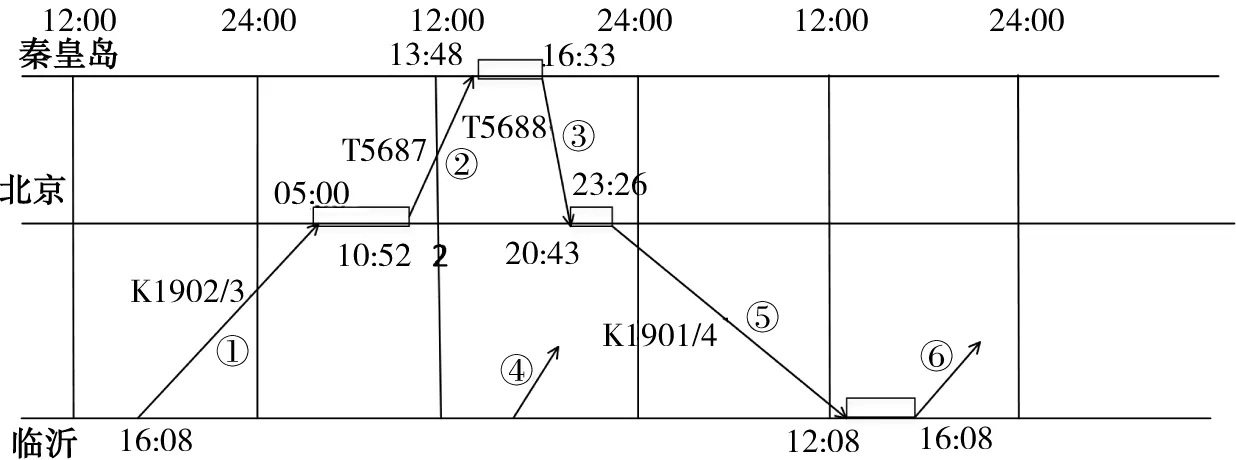
图3 临沂-北京-秦皇岛区段列车车底套用周转
由图1可知,临沂-北京的车底在北京站停留时间过长,利用其在北京站的停留时间去套跑图3的北京-秦皇岛区段,可以减少车底在北京站的停留时间,从而减少车底使用数量。将车底在临沂-北京-秦皇岛-北京-临沂之间的运行看成车底在执行任务,按照既有的运行线运行1次,即执行1次任务,将这些任务根据车次连接起来形成车次连接任务串,这些任务串将某些车次按照一定方式连接起来,从而找到理想的车底套用方案。
2 不固定区段的车底套用模型构建
通过构建车次连接网络图,对初始可行车次连接任务串进行搜索,以每个车次都能被覆盖且仅被覆盖一次为约束条件,以车底使用数量最少为目标函数,建立不固定区段的车底套用模型。
2.1 车次连接网络
车次连接网络由节点及有向边构成。
1)节点
车次连接网络节点分为源节点、始发车站节点、车次节点、终到车站节点和汇节点5类。源节点和汇节点是虚拟节点,表示网络的发散源和汇聚处。始发车站和终到车站是同一个车站,它们分别是某一周期开始时车底的始发车站和该周期结束时车底的终到车站。该周期中车次节点与车底相对应,假设该开行计划中的始发(终到)车站有x个,车底有z个,则该连接网络的节点有(2x+z+2)个。
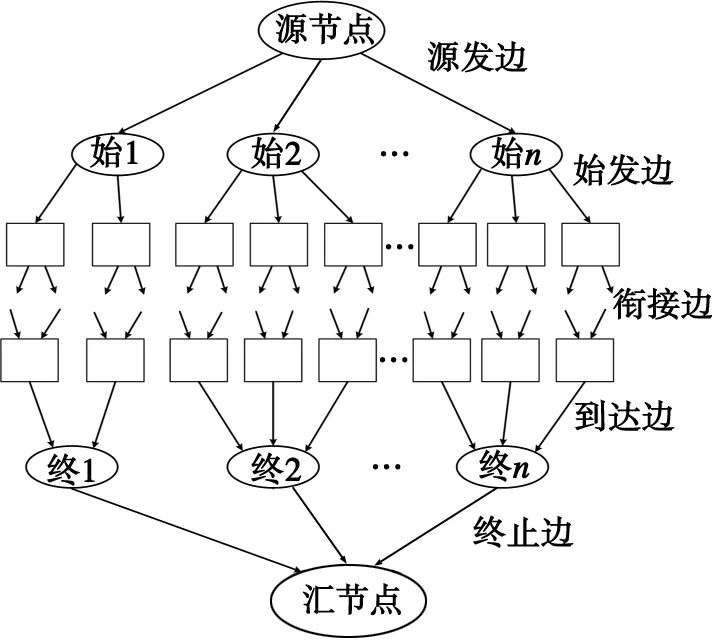
图4 车次连接网络示例图
2)有向边
车次连接网络有向边由源发边、终止边、始发边、到达边、衔接边5部分组成。各始发车站和源节点间用源发边连接,各个始发车站节点与始发车站的车次节点用始发边连接,满足时间和空间限制条件的车次节点之间用衔接边连接,汇节点与终到车站节点之间用终止边连接,各终到车站节点与终到车站的车次节点之间用到达边连接。该连接网络如图4所示,图4中始1、始2、始n分别为第1、2、n个始发车站节点,终1、终2、终n分别为第1、2、n个终到车站节点,方框为对应车次节点。
2.2 车次连接任务串的生成
车次连接任务串的生成分2步:车次连接网络图的构建及根据限制条件从网络图中搜索可行车次连接任务串。
2.2.1 车次连接网络的构建
1)旅客列车时刻表的预处理
普速旅客列车可以与快速旅客列车的车底进行套用,特快旅客列车可以与直达旅客列车车底进行套用。旅客列车时刻表包括列车的出发日期、列车车次、始发车站、始发时刻、终到车站、终到时刻、旅客列车的种类(普速旅客列车、快速旅客列车、特快旅客列车、直达旅客列车)等信息。将包含有始发、终到列车的信息储存于数据库中,先筛选列车种类,将各列车种类的运行计划分开,再筛选始发车站,将各种类列车子集进一步分割成始发车站列车子集。以每个列车的始发车站作为树的根节点,将所有列车的始发车站放在一个专门的集合中,并为车次添加索引,以备求解算法需要。
2)始发车站车次树的构建
在始发车站的集合中依次选择一个车站,以此车站作为树的根节点,遍历列车时刻表,得出所有以此车站为始发车站的集合,然后直接将此集合中每个车次的索引作为此树的子节点。这样构建的树是单层树,根节点是车次的始发车站,子节点是车次的索引,具体实现如图5所示。
3)车次连接网络的构建
遍历所有树的子节点(车次索引),从车次索引得出相对应列车的终到车站。再将子节点和相应的列车时刻表中的终到车站为根节点的树相连,从而构建网络树。具体实现如图6所示。
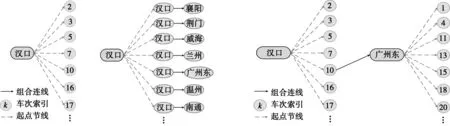
图5 始发车站车次树 图6 车次连接网络
2.2.2 车次连接任务串的搜索
使用深度优先搜索算法对初始可行车次连接任务串进行搜索。
1)车次组合必须满足的条件
①车次组合中的最后1个车次的终到车站为要连接的车次的始发车站。
②2个车次连接时必须满足时间上的接续性,根据始发、终到旅客列车的技术作业过程以及机车乘务员在车站进行交接班作业的时间,将连接的接续时间(列车完成某次任务,到达终点站,到继续担任其他列车任务,并从该站始发这段时间称为列车接续时间,期间包括组织乘客上下车,对列车清洁、检修以及整备等一系列操作过程)初定为不能少于90 min;暂定1个车次组合最多允许运行5个区段。
2)初始可行车次连接任务串的生成
①将旅客列车时刻表按照列车种类进行分割;
②按照始发车站将列车分割成不同种类;
③以各始发车站作为根节点,从其发出的车次节点分裂成出发和到达2个节点;
④将车次的终到节点与从其出发的出发节点合并,不满足衔接时间限制的边直接删掉;
⑤重复步骤③~④,直到再没有满足连接条件的车次为止,得到以各始发车站为根节点的车次连接树;
⑥将终到车站与汇节点连接,形成车次连接网络;
⑦结合深度优先搜索算法,从始发车站开始,搜索网络中的每条路径,在搜索过程中注意车次间的接续时间以及区段数,放弃不符合条件的节点,最后得到初始可行车次连接任务串。
2.3 初始车次连接任务串的优化
车次连接任务串构建完成以后,需要对其进行建模,选出尽可能满足目标函数的车次连接任务串。
1)模型参数定义
已知全线列车运行图,设全线上有始发、终到车站S共n个,始发终到列车L共m列,有
S={s1,s2,…,sn},
L={L1,L2,…,Lm},
式中:S为始发终到车站集合;L为始发终到列车集合。
列车在相邻两列车运行线之间的接续时间为
式中:tfj为列车j的始发时刻;tdi为列车i的终到时刻。
2)目标函数
由于搜索过程中,会出现很多符合条件的车次连接任务串,但是需要选取车底使用数量最少的车次连接任务串组合。
所需的车底数N为
式中T为车底的接续时间。
因为列车的旅行时间tdi~tfi是固定的,所以车底需要数只与车底接续时间T有关,将目标车底需要数量最少转换成车底接续时间总和最小,即

(1)
式中:xg为决策变量,如果选取某车次连接任务串g,则xg=1,求得车底接续时间tij,若没有选取某车次连接任务串g,则xg=0,此时不用计算车底接续时间。
3)约束条件
由于在构造车次连接任务串的过程中已经考虑了公司有关规定以及车站的限制条件,因此,在构造数学模型的过程中约束条件仅需满足每个车次均能被覆盖且仅能被覆盖1次即可,即
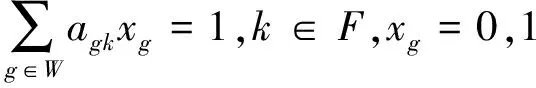
(2)
式中:W为任务串集合;k为某一车次;F为车次集合;当任务串g含有车次k时,agk=1,否则,agk=0。
2.4 遗传算法求解步骤
1)确定寻优参数,进行编码
采用二进制编码的方式对个体进行编码,其中的编码字符串由二进制符号0和1组成,它所构成的个体染色体基因是由一个二进制编码字符串构成。
2)随机产生一组初始解组成初始种群
一般采用随机生成群体规模(记为P)个染色体。已知TSP(旅行商问题)问题的解空间为l!(l=n-1),从l!个解中随机选取1个初始群体的染色体,选取步骤为:
①将随机解sr进行初始化;
②置代数计数器t=1;
③从l-t+1个未访问节点中随机选取一个节点作为sr编码中第i位的sr[i]值,将未访问的节点编号删除;
④t=t+1;如果t≤1则返回第③步,否则执行下一步;
⑤随机可行解sr的获取。
将以上步骤重复若干次,得到初始群体。
3)计算种群中各个个体的目标函数值及其相应的适应度函数值
采用直接转换法将目标函数直接转换为适应度函数,由于本文中所求的目标函数均为求最小值,因此,Fit(f(x))=-f(x)
4)复制
根据适应度函数选择再生个体,适应度高的被复制的概率高,适应度低的则可能被淘汰。
5)交叉
按照一定的交叉概率和交叉方法生成新的个体。
6)变异
按照一定的变异概率和变异方法生成新的个体。
7)终止规则

图7 遗传算法运算流程图
终止条件的判别依据为进化代数达到设定的最大值。
采用进化代数是否已达到设定的最大代数作为终止条件的判别依据。遗传算法的流程图如图7所示。
3 实例分析
以我国4个大型铁路客运枢纽(广州、上海、武汉、北京)为例,以各个客运站的旅客列车时刻表为准备数据,将不固定区段运行的旅客列车进行车底之间的套用。在实际情况中,考虑到旅客列车车底的购置成本昂贵,车底结构可以相匹配的列车之间可以进行套用,比如:普速旅客列车可以与快速旅客列车的车底进行套用,特快旅客列车与直达旅客列车车底进行套用。
将符合条件的普速旅客列车和快速旅客列车重新进行编号,符合条件的普速和快速旅客列车时刻表如表1所示。

表1 普速和快速旅客列车时刻表
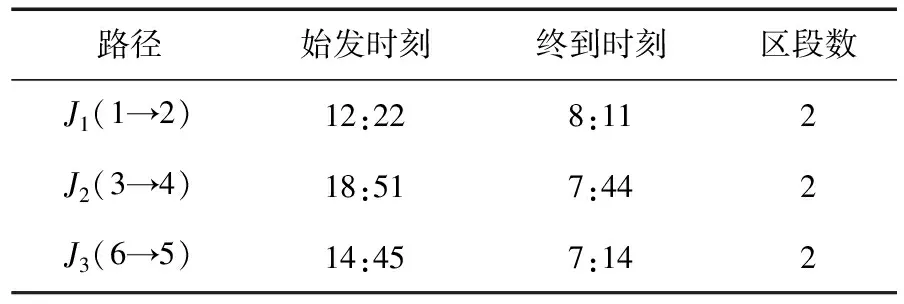
表2 初始可行车次连接任务串
由表1得出的初始可行车次连接任务串如表2所示。从表2看出,由于车次数据量少,没有发现能够进行车底套用的车次。
对直达和特快旅客列车的车次进行重新编号,其时刻表如表3所示。由表3得出的初始可行车次连接任务串如表4所示。
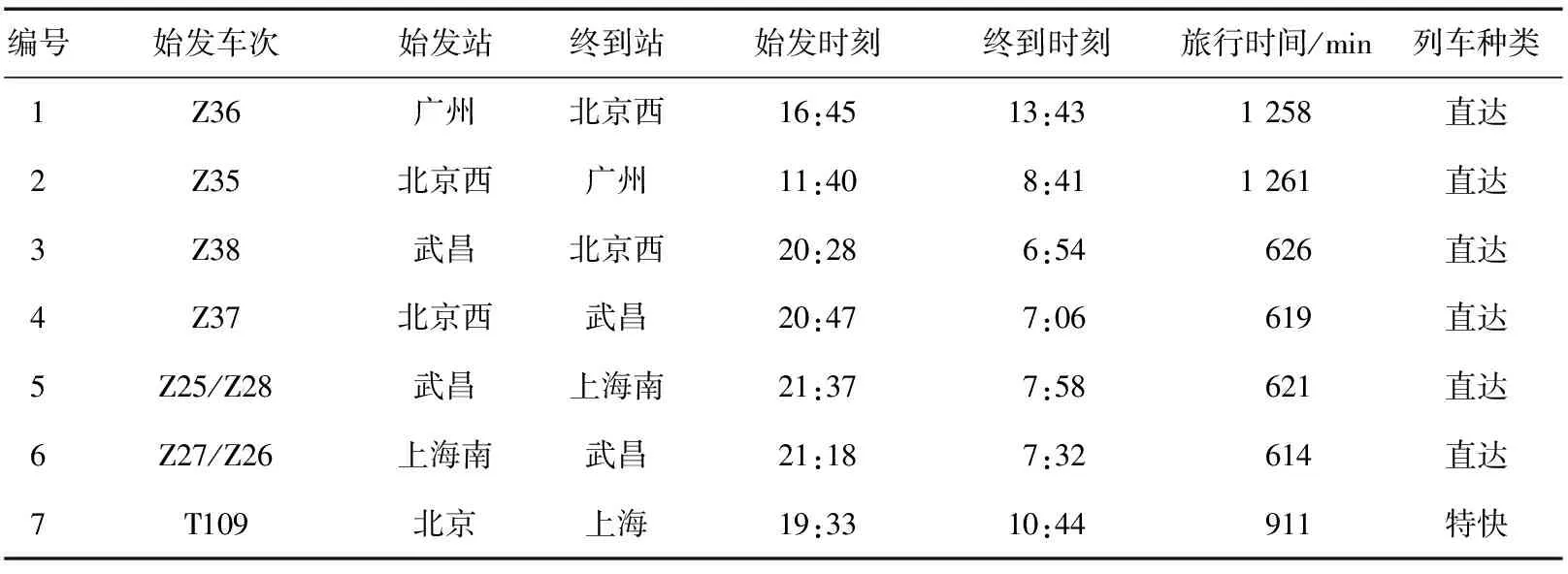
表3 直达和特快旅客列车时刻表
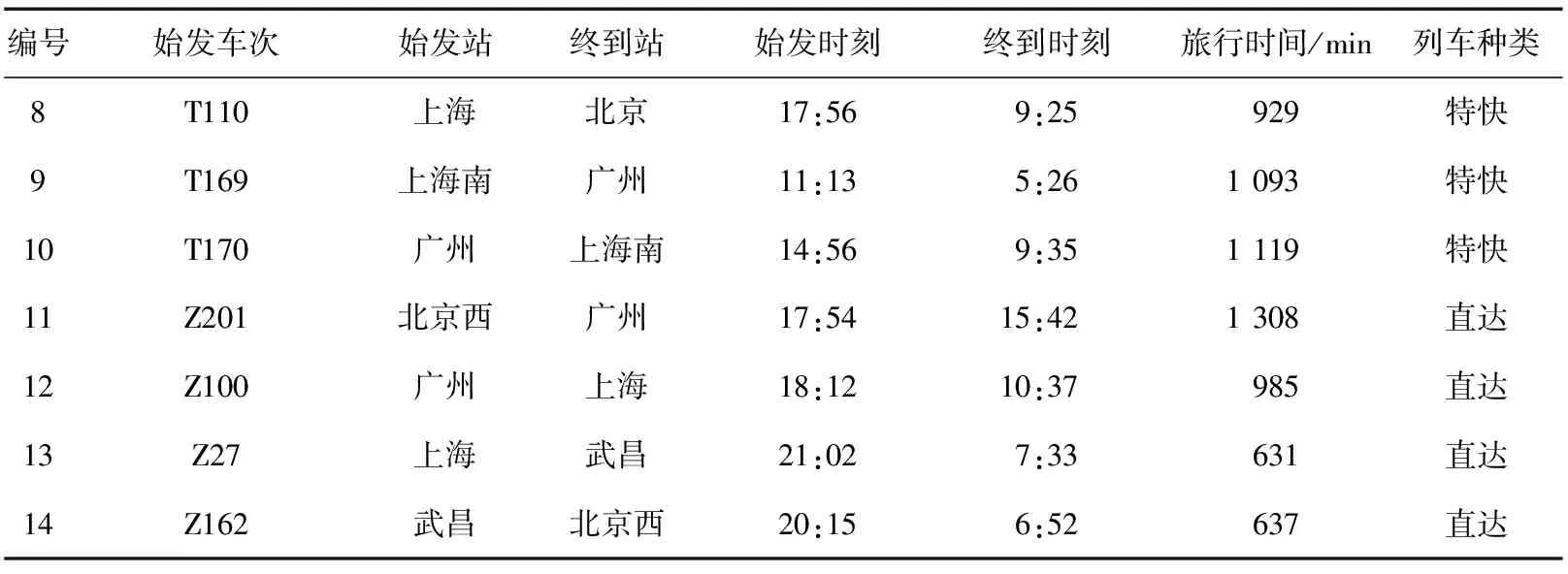
表3(续)

表4 初始可行车次连接任务串
由表4得:W={J1,J2,…,J17},F={1,2,…,14}。
对得出的初始可行车次连接任务串进行优化,以选出符合目标函数的车次连接任务串,首先对初始群体采用二进制编码,由式(2)得矩阵

矩阵agk的每一列为一个初始可行车次连接任务串,每一行的数字为某初始可行车次连接任务串是否选择该车次的结果。“1”为第g个车次连接任务串选取了第k个车次,“0”为第g个车次连接任务串没有选取第k个车次。
在遗传算法工具箱界面设定参数:变量个数为17;演算代数为100;选择方式为精英选择;精英数量为1;交换率为0.2;个体变异率为0.001;基因变异率为0.001。
最终得出的不固定区段车底套用方案如表5、6所示。
从表5可以看出,车底第1天16:45从广州始发,第2天13:43到达北京西站,第2天20:47从北京西出发,第3天7:06到达武昌,第3天21:37从武昌出发,第4天7:58到达上海南站,第4天11:13从上海南站出发,第5天5:26到达广州。可以看出,在不固定区段使用条件下,车底5 d完成了一个周期性的运行。由于上述大部分列车是朝发夕至(或夕发朝至)列车,车底接续时间过长,而进行不固定区段的车底套用以后,车底接续时间明显缩小,使总的车底接续时间减少,由于在式(1)中已经将车底数量的减少转化为车底接续时间的减少,所以所需车底数量减少了。
同理,表6也是车底以5 d为一个周期完成一次运行,车底在站接续时间得到了减少。
表5 不固定区段车底套用方案一

编号车次始发站终到站始发时刻终到时刻1Z36广州北京西16:4513:434Z37北京西武昌20:477:065Z25/Z28武昌上海南21:377:589T169上海南广州11:135:26
表6 不固定区段车底套用方案一

编号车次始发站终到站始发时刻终到时刻14Z162武昌北京西20:156:5211Z201北京西广州17:5415:4212Z100广州上海18:1210:3713Z27上海武昌21:027:33
4 结语
本文分析列车固定区段运用方式和不固定区段运用方式的特点,建立不固定区段的车底套用模型。通过实例可以看出:车底在站接续时间减少,从而达到减少车底数量的目的。由于案例的数据量偏少,节省的车底组数有限,同时由于不固定区段车底套用会导致乘务工作复杂多变,如何突破车底配属限制,使车底在不固定区段运行,从而提高车底使用效率、减少车底使用组数和乘务工作时间,是下一步要研究的重点。
[1]刘超.城市轨道交通大小交路嵌套模式下车体运用优化模型和方法[D].北京:北京交通大学,2012. LIU Chao.Optimization model and method of urban railway transit vehicle use planning with long and short routing[D].Beijing:Beijing Jiaotong University,2012.
[2]陈华群.动车组运用计划编制系统相关问题研究[D].成都:西南交通大学,2007. CHEN Huaqun.Research on the relative problems of motor train-set scheduling system[D].Chengdu:Southwest Jiaotong University,2007.
[3]朱昌锋,李引珍.基于既定列车运行图的铁路旅客列车车底套用协同优化研究[J].中国铁道科学,2014,35(3):120-128. ZHU Changfeng,LI Yinzhen.Collaborative optimization on assignment of passenger train stock based on given train diagram[J].China Railway Science,2014,35(3):120-128.
[4]肖益帆,朱昌锋.基于模拟退火算法的铁路旅客列车车底套用优化研究[J].铁道科学与工程学报,2012,9(5):108-113. XIAO Yifan,ZHU Changfeng.Railway train set assignment based on simulated annealing algorithm[J].Journal of Railway Science and Engineering,2012,9(5):108-113
[5]鲁红珍.航空公司机组航班任务串优化方法研究[D].广汉:中国民用航空飞行学院,2012. LU Hongzhen.Research on airline crew pairing problem optimization methods[D].Guanghan:Civil Aviation Flight University of China,2012.
[6]李金龙.旅客列车车底运用优化系统的研究与开发[D].北京:北京交通大学,2006. LI Jinlong.Passenger train scheduling optimization system research and development[D].Beijing:Beijing Jiaotong University,2006.
[7]邵俊.基于遗传算法的机组任务配对研究[D].南京:南京航空航天大学,2006. SHAO Jun.Air crew pairing study based on genetic algorithm of airlines in China[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2006.
[8]都业富.航班串优化方法[J].系统工程理论与实践,1995,6(8):75-80. DU Yefu.Flight string optimization method[J].Systems Engineering-Theory & Practice,1995,6(8):75-80.
[9]徐刚,赵剑梅.不同车底运用方式下旅客列车成本计算模型研究[J].技术经济,2006,5(1):84-86. XU Gang,ZHAO Jianmei.Research on the calculation model of the passenger train cost of different vehicle use mode[J].Technology Economics,2006,5(1):84-86.
[10]王甦男,贾俊芳.旅客运输[M].北京:中国铁道出版社.2011. WANG Sunan,JIA Junfang.Passenger transportation[M].Beijing:China Railway Publishing House,2011.
[11]BURKOLTER Dan,HERRMANN Thomas,CAIMI Gabriel.Generating dense railway schedules[J].Advanced OR and AI Methods in Transportation,2005:290-297.
[12]ERWIN Abbnk,BIANCA van den Berg,LEO Kroon,et al.Allocation of railway rolling stock for passenger trains[J].ERIM Report Series Research in Management,2002,4(47):1-16.
[13]RICHARD Freling,RAMON M Lentink,LEO Kroon,et al.Shunting of passenger train units in a railway station[J].ERIM Report Series Research in Management,2002(74):1-19.
[14]PETER Bruckner,JOHANN Harkin,THOMAS Rolfs.Routing of railway carriages:a case study[J].Faculty of Mathematical Sciences,1999,20(149):1-29.
[15]ARIANNA Alfieri,RUTGERS Groot,LEO Kroon,et al.Efficient circulation of railway rolling stock[J].ERIM Report Series Research in Management,2002,15(110):1-18.
[16]LEI Nia,INGO A Hansen.System analysis of train operations and track occupancy at railway stations[J].European Journal of Transport and Infrastructure Research,2005,5(1):31-54.
[17]DAILYDKA Stasys,LINGAITIS Vitiates.A study on the options of means for railway passenger transportation[J].Transport Problems,2012,1(7):53-61.
[18]JONAS Butkevicius,LEONES Povilas Lingaitis,GEDIMINAS Vaiciunas.Rolling stock planning for passenger transportation[J].Transport,2004,10(5):202-206.
[19]WANEVELD P J Z,ROONL G K,OMEIJN H E R,et al.Routing trains through railway stations model formulation and algorithms[J].Transportation Science,1996,30(3):181-194.
[20]RYU J,DUA V PISTIKOPOULOS E N.A bi-level programming framework for enterprise-wide process networks under uncertainty[J].Computers and Chemical Engineering,2004,28(6):1121-1129.
(责任编辑:杨秀红)
Optimization of Set Assignment of Passenger Train in Uncertain Sections of Railway
CUIShanshan
(SchoolofTransportationandLogistics,SouthwestJiaotongUniversity,Chengdu610031,China)
Through the analysis of application of the current passenger train set,this article puts forward that the application of the train set assignment can increase its efficiency and decrease the connecting time of the train set assignment at the station.The paper searches for the initially feasible train number connection duty strings by constructing train number connection network diagram,establishes the model of the train set assignment in uncertain sections,in which each train number is covered and only once as the constraint condition,and the minimum number of the train set assignment in use is the objective function,and finally adopts the genetic algorithm to solve the problem.The model is used to verify the operation conditions of passenger trains at some large passenger stations of four areas such as Beijing,Wuhan,Guangzhou and Shanghai.The results show that the connecting time of the train set assignment decreases and the train set assignment is less used in quantities.
passenger train; uncertain section; train set assignment; genetic algorithm
2016-07-20
崔姗姗(1992—),女,河南灵宝人,硕士研究生,主要研究方向为运输组织优化,E-mail:834612552@qq.com.
10.3969/j.issn.1672-0032.2016.04.006
U292.4
A
1672-0032(2016)04-0036-09

