基于多学科设计法的汽车双横臂独立悬架优化设计
赵玉霞,林建飞,郑泉
(1.滁州职业技术学院,安徽滁州 239000;2.安徽农业大学 工学院,安徽合肥 230036)
基于多学科设计法的汽车双横臂独立悬架优化设计
赵玉霞1,林建飞2,郑泉2
(1.滁州职业技术学院,安徽滁州 239000;2.安徽农业大学 工学院,安徽合肥 230036)
提出一种基于多学科优化设计的双横臂独立悬架优化设计方法。以某款汽车的双横臂独立悬架为研究对象,构建主销后倾角最小、外倾角和前束角变化量最小的多目标优化函数;集成ISIGHT和ADAMS/CAR软件,并对其进行多学科优化设计。优化结果表明:优化后主销后倾角相应减小2°,外倾角和前束角变化范围均减少0.45°和0.5°。经试验验证,悬架转向轻便性和综合性能得到改善。
悬架;双横臂;遗传算法;多学科优化
双横臂式独立悬架广泛应用于现代汽车上,其运动特性直接影响汽车操纵稳定性、转向轻便性和轮胎使用寿命等[1-2]。国内外诸多学者在双横臂悬架优化设计方面进行了大量的研究[3-6],文献[7]利用多目标遗传算法对轮胎滑移和倾角的变化进行优化,得出双横臂悬架轮胎滑移和外倾角的变化关系及其悬架导向杆系参数;文献[8]采用统一目标法将多目标函数转化为单目标函数,对前轮定位参数进行了优化。
多学科设计优化方法(multidisciplinary design optimization,MDO)作为一种新型的优化设计方法已经在多种行业得到应用,该方法是充分利用和探索系统中相互作用的协同机制来设计复杂系统和子系统的方法论,充分考虑各子系统间的耦合关系,并通过协调各子系统间的关系寻求系统级的整体最优解[9-11]。
本文以某款汽车的双横臂独立悬架为研究对象,建立主销后倾角最小、外倾角和前束角变化量最小的目标函数,基于多学科优化设计方法,集成ISIGHT、 ADAMS/CAR环境下构建双横臂独立悬架多学科优化平台,对其进行优化设计。
1 双横臂悬架运动特性分析
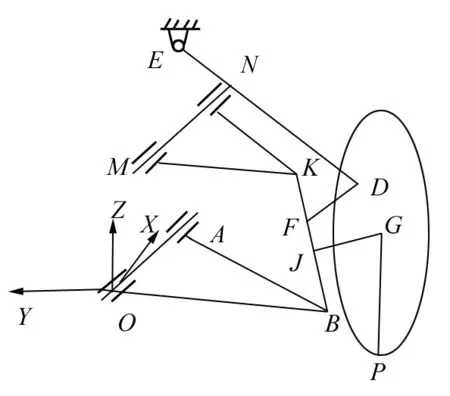
图1 双横臂式独立悬架空间结构简图
双横臂式独立悬架空间拓扑结构如图1所示,图中OAB为下摆臂,绕轴线OA转动;MNK为上摆臂,绕轴线MN转动;K(xK,yK,zK)、B(xB,yB,zB)点分别为上下球节点,BK为主销轴线;G(xG,yG,zG)点为车轮中心,车轮轴线GJ交BK于J(xJ,yJ,zJ)点;P(xP,yP,zP)点为轮胎接地点;转向节臂DF交BK于F点,DF⊥BK;E、D点分别为横拉杆内外球节点。运用空间机构运动学原理,对悬架进行运动学分析计算,为悬架运动轨迹的研究提供理论参照[12-14]。前轮定位参数表达式为:主销内倾角α=arctan〔(yK-yB)/(zK-zB)〕,主销后倾角β=arctan〔(xK-xB)/(zK-zB)〕,前轮外倾角γ=arctan〔(yP-yG)/(zP-zG)〕,前轮前束量Δ=arctan〔(xG-xJ)/(yG-yJ)〕。
2 双横臂独立悬架多学科优化
2.1 设计变量

图2 双横臂悬架运动学模型
基于ADAMS/CAR软件建立双横臂悬架运动学模型如图2所示。由于设计变量较多(6个关键点,总共18个设计变量),基于灵敏度分析方法对设计变量进行分析,设计变量约束上下变动,设计响应目标为主销后倾角、外倾角和前束角,进行512次部分迭代计算,计算结束后,得出灵敏度分析结果,如表1所示。在K模式下,利用灵敏度分析方法,在模型中依次调整每个因素并进行仿真分析,结果表明下摆臂后点(hpl_lca_rear)、上摆臂前点(hpl_uca_front)对悬架相关运动学参数的优化作用不明显,故不予考虑。整理表1灵敏度分析结果得出对响应目标变化影响较大的硬点坐标为:下摆臂前点(hpl_lca_front)y和z坐标;下摆臂外点(hpl_lca_outer)x坐标;上摆臂外点(hpl_uca_outer)x、y和z坐标;上摆臂后点(hpl_uca_rear)y和z坐标,共4个点的8个方向坐标为设计变量。

表1 悬架关键点灵敏度分析表
2.2 目标函数
悬架系统运动关系复杂、子系统之间相互影响,单纯基于某一项性能的优化往往会导致另一项性能的降低[15-16]。因此,在要求主销后倾角减小的同时,需满足前束角和外倾角的变化量最小,此时主销后倾角、前束角和外倾角的多目标优化问题,使用以下公式进行优化:
F1(Xβ)=min{Xβi},X1∈Xβ,
(1)

(2)

(3)
F(X)=ω1F1(Xβ)+ω2F2(XΔ)+ω3F3(Xγ),
(4)
式中:n为仿真迭代总次数,n=256;Xβ、XΔ、Xγ分别为主销后倾角、前束角和外倾角仿真计算值;X1、X2、X3分别为设计状态下主销后倾角、前束角和外倾角初值,X1=5.3、X2=0.1、X3=-1.0;F1(Xβ)、F2(XΔ)、F3(Xγ)分别为主销后倾角、前束角和外倾角对应目标函数,设计状态下边界条件为0≤F1(Xβ)≤10、-1.0≤F2(XΔ)≤10、-3.0≤F3(Xγ)≤-0.5;F(X)为多目标优化函数,定义为F(X)函数值越小越好;ω1、ω2、ω3为权重系数,通过引入层次分析法理论[17-19],在遗传算法的编码过程中对各变量进行权重赋值,使得对多目标优化函数影响较大的目标函数赋予较大的权重,从而更好地发挥各组成部分的作用,通过赋值计算得出ω1=0.4,ω2=ω3=0.3为最优权重系数。
3 多学科优化设计
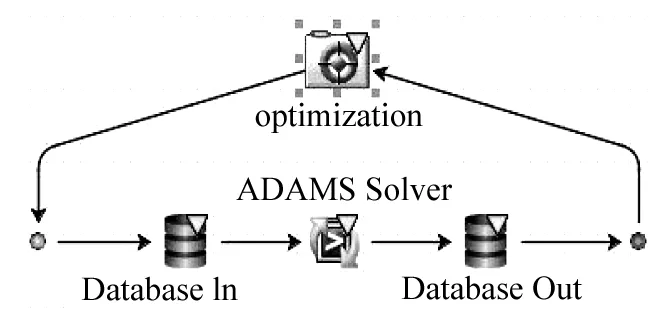
图3 ISIGHT集成ADAMS/CAR
利用多目标遗传算法对相关硬点空间坐标进行多学科优化,以双横臂独立悬架模型为输入,在ISIGHT软件中集成ADAMS对输入进行解析,创建设计变量之间的映射关系,经ADAMS求解器计算分析并生成输出文件,再经ISIGHT解析完成一次循环[20-22],如图3所示。优化前后设计变量对比如表2所示,优化前后主销后倾角、前轮外倾角、前束角变化如图4所示。
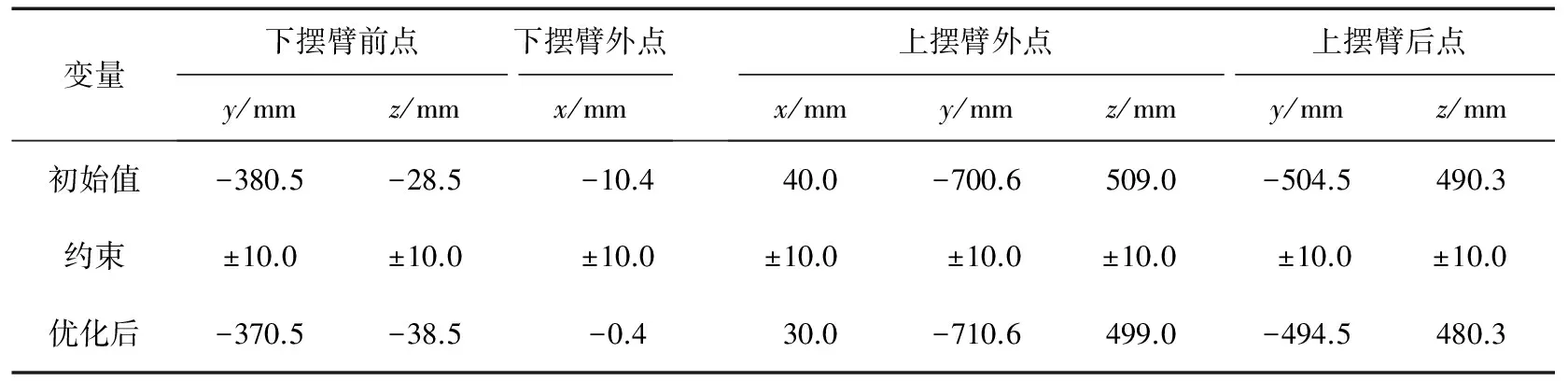
表2 硬点坐标参数优化前后对比

a)主销后倾角随轮跳变化曲线 b)前束角随轮跳变化曲线 c)前轮外倾角随轮跳变化曲线图4 悬架优化前后运动特性对比
由表2可知:下摆臂前点右移10 mm,下移10 mm,下摆臂外点后移10 mm,上摆臂外点前移10 mm,左移10 mm,下移10 mm;上摆臂后点右移10 mm,下移10 mm。
优化结果表明:优化后主销后倾角变小,外倾角和前束量变化范围较优化前都有所改善。优化前前轮外倾角变化范围-2.1°~-0.6°,变化量1.5°;优化后变化范围-0.8°~-1.85°,变化量1.05°,变化量减小了0.45°;优化前前束角变化范围-0.15°~0.75°,变化量0.9°;优化后变化范围0°~0.4°,变化量0.4°,变化量减小了0.5°,在轮跳过程中,一般要求前束量变化范围越小越好;为避免转向沉重,汽车主销后倾角不宜过大,优化后主销后倾角相应减小了2°,变化范围在2.2°~4.0°。经K&C试验台验证,如图5所示,主销后倾角满足设计需求,悬架转向轻便性得到了有效提高。
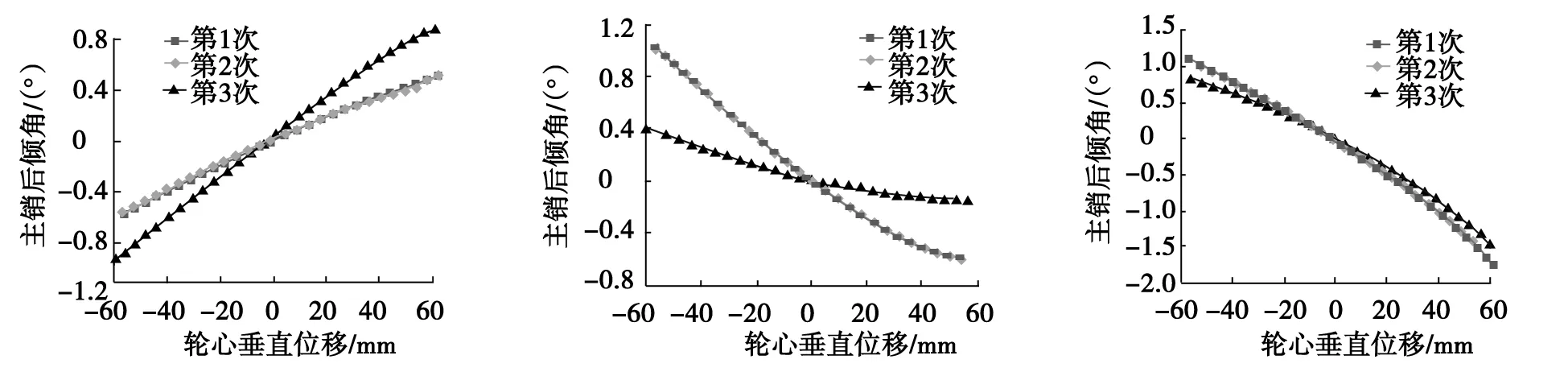
a)主销后倾角随轮跳变化曲线 b)前束角随轮跳变化曲线 c)外倾角随轮跳变化曲线图5 双横臂悬架K&C试验数据图
4 结语
构建了基于多学科优化设计方法的双横臂式独立悬架多目标优化模型,集成ISIGHT和ADAMS软件对其进行优化设计;优化后主销后倾角变小,前束角变化量和外倾角变化量减小并经试验验证,提高转向轻便性的同时改善了悬架综合性能,实现了预期目标。
[1]陈家瑞.汽车构造(下册)[M].北京:机械工业出版社,2006.
[2]余志生.汽车理论[M].3版.北京:机械工业出版社,2005.
[3]MAHMOOD-KALEIBAR M,JAVANSHIR I,ADSADI K,et al.Optimization of suspension system of off-road vehicle for vehicle performance improvement[J].Journal of Central South University of Technology,2013,20(4):902-910.
[4]陈黎卿,王启瑞,陈无畏,等.基于ADAMS的双横臂扭杆独立悬架操纵稳定性分析[J].合肥工业大学学报(自然科学版),2005,28(4):341-345. CHEN Liqing,WANG Qirui,CHEN Wuwei,et al.Analysis of handling stability of torsion-bar double wishbone independent suspension based on ADAMS software[J].Journal of Hefei University of Technology(Natural Science),2005,28(4):341-345.
[5]胡芳,陈无畏.基于非线性模型的汽车空气悬架系统模糊控制研究[J].合肥工业大学学报(自然科学版),2005,28(7):772-777. HU Fang,CHEN Wuwei.Fuzzy control research on automotive air suspension system based on the non-linear model[J].Journal of Hefei University of Technology(Natural Science),2005,28(7):772-777.
[6]胡艳云,干年妃,刘良.某轿车的双横臂独立悬架优化设计[J].计算机仿真,2015,32(1):174-178,214. HU Yanyun,GAN Nianfei,LIU Liang.Optimization of double wishbone suspension for car[J].Computer Simulation,2015,32(1):174-178,214.
[7]莫旭辉,钟志华,韩旭,等.基于多目标优化的菱形车双横臂悬架运动学分析[J].中国机械工程,2009(3):374-377. MO Xuhui,ZHONG Zhihua,HAN Xu,et al.Kinematics analysis of double wishbone suspension based on multi-objective optimizaton[J].China Mechanical Engineering,2009(3):374-377.
[8]李瑜婷,赵治国,章桐.基于ADAMS的双横臂悬架性能多目标优化研究[J].机械设计与制造工程,2009,38(17):30-34. LI Yuting,ZHAO Zhiguo,ZHANG Tong.The ADAMS-based multi-objects optimization of double beams vehicle suspension[J].Machine Design and Manufacturing Engineering,2009,38(17):30-34.
[9]王平,郑松林,吴光强.基于协同优化和多目标遗传算法的车身结构多学科优化设计[J].机械工程学报,2011,47(2):102-108. WANG Ping,ZHENG Songlin,WU Guangqiang.Multi-disciplinary design optimization of vehicle body structure based on collaborative optimization and multi-objective genetic algorithm[J].Journal of Mechanical Engineering,2011,47(2):102-108.
[9]姜武华.多学科优化方法在汽车底盘设计中的应用研究[D].合肥:合肥工业大学,2014. JIANG Wuhua.Application of multi-discipline design optimization in automotive chassis[D].Heifei:Hefei University of Technology,2014.
[11]赵婷.汽车转向与悬架集成系统多学科设计方法研究[D].南京:南京航空航天大学,2014. ZHAO Ting.Multidisciplinary design method research of automotive steering and suspension integrated system[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2014.
[12]杨红强,翁建生.双横臂独立悬架的仿真与优化研究[J].机械科学与技术,2011,30(10):1683-1687. YANG Hongqiang,WENG Jiansheng.Simulation and optimization of the double wishbone suspension[J].Mechanical Science and Technology for Aerospace Engineering,2011,30(10):1683-1687.
[13]陈黎卿,陈无畏,何钦章.双横臂扭杆独立悬架多目标遗传优化设计[J].中国机械工程,2007,18(17):2122-2125. CHEN Liqing,CHEN Wuwei,HE Qinzhang.Multi-objective heredity optimization design of torsion-bar wishbone suspension[J].China Mechanical Engineering,2007,18(17):2122-2125.
[14]何磊,陈辛波,黄露,等.双横臂独立悬架导向机构优化仿真及参数化台架实验验证[J].机械科学与技术,2015,34(2):282-286. HE Lei,CHEN Xinbo,HUANG Lu,et al.Simulation optimization of double wishbone independent suspension guide mechanism and parametric bench test[J].Mechanical Science and Technology for Aerospace Engineering,2015,34(2):282-286.
[15]王军,姜青松,任启丰.基于遗传算法的客车动力性与经济性的优化匹配[J].山东交通学院学报,2012,20(4):5-8. WANG Jun,JIANG Qingsong,REN Qifeng.Optimal matching of coach power performance and economy based on genetic algorithm[J].Journal of Shandong Jiaotong University,2012,20(4):5-8.
[16]陈林,蒋德云,李杰,等.某轻型卡车驾驶室翻转机构的结构设计与优化[J].山东交通学院学报,2013,21(2):9-13. CHEN Lin,JIANG Deyun,LI Jie,et al.The design and optimization of the tilting mechanism for the cab of a light truck[J].Journal of Shandong Jiaotong University,2013,21(2):9-13.
[17]廖红强,邱勇,杨侠,等.对应用层次分析法确定权重系数的探讨[J].机械工程师,2012(6):22-25. LIAO Hongqiang,QIU Yong,YANG Xia,et al.A Study of weight coefficient computing method based on AHP[J].Mechanical Engineer,2012(6):22-25.
[18]魏代俊,王能发.关于层次分析法中群体决策权重系数确定的探讨[J].湖北民族学院学报(自然科学版),2007,25(2):146-147. WEI Daijun,WANG Nengfa.Study on the determination of weight coefficients in AHP group decision[J].Journal of Hubei University for Nationalities(Natural Sciences Edition),2007,25(2):146-147.
[19]王化吉,宗长富,管欣,等.基于模糊层次分析法的汽车操纵稳定性主观评价指标权重确定方法[J].机械工程学报,2011,47(24):83-90. WANG Huaji,ZONG Changfu,GUAN Xin,et al.Method of determining weights of subjective evaluation indexes for car handling and stability based on fuzzy analytic hierarchy process[J].Journal of Mechanical Engineering,2011,47(24):83-90.
[20]李仕锋,黄雪娇,曹源文.基于ADAMS/Car的客车平顺性仿真研究[J].山东交通学院学报,2011,19(4):8-11. LI Shifeng,HUANG Xuejiao,CAO Yuanwen.Design of simulation system for estimation of vehicle manipulation stability[J].Journal of Shandong Jiaotong University,2011,19(4):8-11.
[21]常媛媛,段业广,雍文亮,等.基于ISIGHT的重型汽车空气悬架系统多目标优化设计[J].山东交通学院学报,2013,21(3):20-25. CHANG Yuanyuan,DUAN Yeguang,YONG Wenliang,et al.Multi-objective optimization design of air suspension system for heavy vehicle based on ISIGHT[J].Journal of Shandong Jiaotong University,2013,21(3):20-25.
[22]程贤福,刘艳军,林彧群.汽车双横臂悬架参数稳健优化设计[J].机械科学与技术,2016(9):1421-1425. CHENG Xianfu,LIU Yanjun,LIN Yuqun.Robust optimization design of double wishbone suspension system for automotive[J].Mechanical Science and Technology for Aerospace Engineering,2016(9):1421-1425.
(责任编辑:郎伟锋)
Optimization Design of Double-wishbone Independent Suspension of Car Based on MDO
ZHAOYuxia1,LINJianfei2,ZHENGQuan2
(1.ChuzhouVocationalandTechnicalCollege,Chuzhou239000,China; 2.CollegeofEngineering,AnhuiAgriculturalUniversity,Hefei230036,China.)
An optimum design method of the double wishbone independent suspension based on the multidisciplinary design optimization (MDO) is presented.By taking the double wishbone independent suspension of a car model as the research subject,the multi-objective optimization functions of the minimum caster,camber and toe angle change is constructed and the multidisciplinary design optimization is made based on the integrated ISIGHT and ADAMS / CAR software.The optimization results show that the optimized caster angle decreases by 2° correspondingly,and the range of camber and toe angles decreases by 0.45° and 0.5° respectively.The experiments verify that the steering portability and overall performance of suspension are improved.
suspension;double-wishbone;genetic algorithm;MDO
2016-09-09
安徽省高校自然科学重点项目(KJ2015A305)
赵玉霞(1965—),女,安徽淮北人,讲师,主要研究方向为机械设计,E-mail: 362770001@qq.com.
10.3969/j.issn.1672-0032.2016.04.003
U463.33
A
1672-0032(2016)04-0012-06

