合情推理在三角函数解题中的应用研究
王春华●
江苏省泰州市姜堰区罗塘高级中学(225500)
合情推理在三角函数解题中的应用研究
王春华●
江苏省泰州市姜堰区罗塘高级中学(225500)
为加强高中生的三角函数解题能力的培养,本文对合情推理在三角函数解题中的应用问题展开了研究,具体探讨了归纳推理、类比推理和特殊化推理几种合情推理方法的应用问题.
合情推理;高中数学;三角函数解题;应用
作为重要的数学解题工具,三角函数的学习对高中生至关重要.但就实际情况而言,高中生大多对三角函数的学习缺乏信息,无法较好地应用三角函数性质和公式解题.而在三角函数解题中应用合情推理,则能够帮助学生完成三角函数中的变量关系的主动探究,从而更好地完成三角函数公式的记忆和运用.
一、归纳推理在三角函数解题中的应用
所谓的归纳总结推理方式,其实就是结合实例对三角函数中的自变量和因变量的关系进行理解,从而帮助学生顺利完成函数表达式的推导和理解.采取该种方式,能够使学生更好地发现现实函数问题中的各个变量间的关系,从而完成函数的归纳.
例1f(x)在R上为奇函数,满足f(a-x)=f(x),证明f(x)为周期函数,并且周期为2a.
证明 ∵f(a+x)=f[a-(-x)]=f(-x)=-f(x),
∴f(2a+x)=-f(a+x)=f(x).
由诱导公式可知,若奇函数y=sinx满足sin(π-x)=sinx,则y=sinx为周期函数,周期为2π.
通过解答例题,则能够帮助学生理解诱导公式是如何推导出来的.进一步证明函数f(x)为R上的偶函数,满足f(a-x)=f(x),则f(x)为周期函数,并且周期为2a.进而能够通过归纳掌握“奇变偶不变,符号看象限”这一基本的三角函数规律.
二、类比推理在三角函数解题中的应用
在学习三角函数的过程中,将接触到正弦函数、正切函数、余弦函数和余切函数这四个主要函数.通过类比分析,则可以发现这四个函数都有奇偶性、周期性和对称性等函数特性.在类比推理的过程中,不仅能够掌握不同三角函数的相同点,还能够实现不同函数的区分,从而避免在三角函数解题中出现错误.
例2 函数f(x)在R上的图象如果分别关于直线x=a和x=b对称,且a>b,则g(x)为周期函数,并且周期为T=2(a-b).
分析 正弦函数y=sinx的特性可以发现,sinx为周期函数,图象为轴对称图形.在函数y=sinx的对称轴上,若存在x=π/2和x=-π/2两条直线,则函数周期为T=2[π/2-(-π/2)].通过对三角函数图象性质进行类比推理,则可以完成例题的求解.
证明 由题可知,f(x)=f(2a-x),f(x)=f(2b-x),
∴f[x+2(a-b)]=f[2a-(2b-x)]=f(2b-x)=f(x).
∴2(a-b)为f(x)的一个周期.
例3 函数f(x)和g(x)在R上不恒为0,并且满足f(x+y)=f(x)g(y)+f(y)g(x)和f(x-y)=f(x)g(y)-f(y)g(x),则函数f(x)和g(x)分别为奇函数和偶函数.
在求解该问题时,可以利用三角函数进行类比推理,从而利用三角函数解题.因为,正弦函数y=sinx满足sin(x+y)=sinxcosy+sinycosx和sin(x-y)=sinxcosy-sinycosx,并且sinx为奇函数,cosx为偶函数.
证明 ∵f(0-0)=f(0)g(0)-f(0)g(0),
∴f(0)=0.
∴f(x+0)=f(x)g(0)-f(0)g(x)=f(x)g(0),
且f(0-x)=f(0)g(x)-f(x)g(0)=-f(x)g(0),
可得f(-x)=-f(x),所以f(x)为奇函数.
∵f(x+(-x))=f(x)g(-x)+f(-x)g(x)
=f(x)[g(-x)-g(x)]=0,且f(x)不恒为零,
∴g(-x)=g(x),所以g(x)为偶函数.
三、特殊化推理在三角函数解题中的应用
在学生难以理解三角函数表达形式的情况下,教师可以结合特殊例子帮助学生通过特殊化推理研究函数性质.在推导一些三角函数性质时,教师可以引导学生取特殊角,从而帮助学生更好地掌握这部分内容.
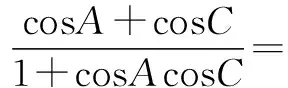

在高中数学教学中,如何运用三角函数解题一直是困扰高中生的问题.为帮助学生更好地掌握和运用三角函数性质,教师还要应用合情推理的方法帮助学生理解具体的函数知识,并且掌握函数中的各个变量的关系,从而更好地进行三角函数解题.
[1]黄春雷.类比推理在高中数学教学中的作用[J].成功(教育),2013,20:72.
[2]殷瑞鑫.合情推理在高中数学函数中的应用研究[J].中学课程辅导(教师通讯),2015,24:78.
G632
B
1008-0333(2016)34-0025-01

