追踪高考导数涉及的证明问题

寇桂宴● 陈国林●

赣南师范大学科技学院(341000) 安徽省利辛高级中学(236700)

追踪高考导数涉及的证明问题

寇桂宴● 陈国林●

赣南师范大学科技学院(341000) 安徽省利辛高级中学(236700)

纵观高考命题，近几年全国卷关于对导数的考查要求较高，导数问题是中学数学与高等数学相互连接的重要部分，一直充当着高考压轴题的角色.

通过对全国卷导数试题部分进行分析，近几年，导数部分结合证明问题考查可谓层出不穷，已经成为高考的一个“大餐”，成为了拉开分数的一个重要部分.如何解决高考导数中的证明问题呢？下面用例题说明.

一、一次求导的基础证法

例题1 (2015年全国卷2第21题)设函数f(x)=emx+x2-mx.

证明：f(x)在(-∞，0)单调递减，在(0，+∞)上单调递增.

解析f′(x)=m(emx-1)+2x.若m≥0，则当x∈(-∞，0)时，emx-1≤0,f′(x)<0；当x∈(0，+∞)时，emx-1≥0，f′(x)>0.若m<0，则当x∈(-∞，0)时，emx-1>0，f′(x)<0；当x∈(0，+∞)时，emx-1<0，f′(x)>0.所以，f(x)在(-∞，0)单调递减，在(0，+∞)上单调递增.

评注 一阶导数证明问题，属于导数中的基础问题，主要根据导函数与0之间的关系来证明函数的单调性的.

二、二次求导的朴实证法

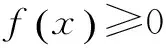
解析 (1)因为f′(x)=-sinx+ax，a∈R,令g(x)=-sinx+ax则g′(x)=-cosx+a，所以当a≥1时，g′(x)≥0，即g(x)在R上单调递增.又g(0)=0，所以当x∈[0,+∞)上为增函数，在(-∞,0)上为减函数，又f(0)=0，所以当x∈[0,+∞)时，f(x)≥0，当x∈(-∞,0)时，f(x)>0，故f(x)≥0对x∈R恒成立，即当a≥1时，f(x)≥0，当且仅当x=0时，f(x)=0，故当a≥1时，f(x)有唯一零点.

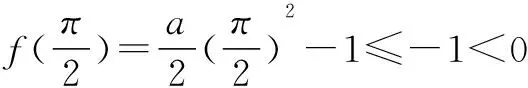
综上，若f(x)≥0时，a的取值范围为[1,+∞).

评注 二次求导的原因主要是在一次求导后无法判断极值点或者极值点的判断相对比较复杂，另外在题目的设置中一般二次求导后对于一阶导数都具有单调性.

三、不可忽视的数学归纳证法

(1)讨论函数G(x)=f(x)-g(x)的单调性；

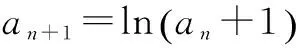
评注 数学归纳法在证明题中一直扮演着不可或缺的地位，在导数中通常情况下如果遇到与数列结合的时候，数学归纳法证明会显得相对明了.因此在遇到证明题的时候不可忘却数学归纳法，因为在阅卷中是根据解题步骤得分，相比之下其可以让你多获分.

四、构造函数的巧妙证法

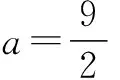
(2)在(1)中当a=0时，函数y=f(x)的图象上任意不同的两点A(x1,y1),B(x2,y2)，线段AB的中点为C(x0,y0)，记直线AB的斜率为k，试证明：k>f′(x0)．

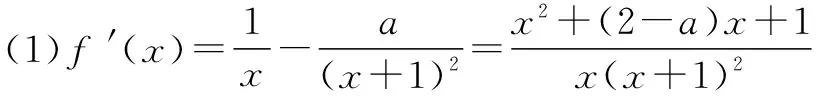
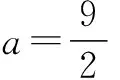
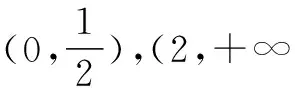
(2)证明：当a=0时，f(x)=lnx.

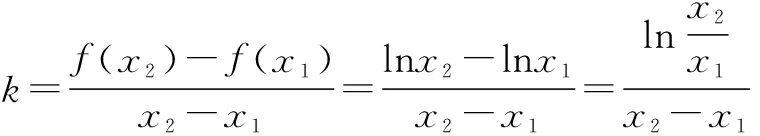
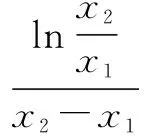
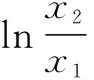
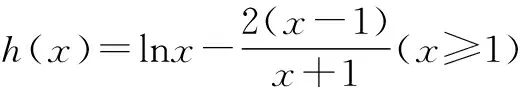
∴h(x)在[1,+∞)上为增函数.

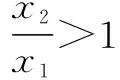
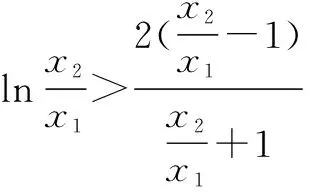
评注 构造函数的方法也是导数压轴题常考的内容之一.在利用构造函数时一般使用于变形构造函数证明不等式和替换构造不等式证明不等式.

五、放缩法的机智证法

例题5 (2016年安庆二模)已知函数f(x)=lnx+ax，a∈R.

(1)讨论函数f(x)的单调性；

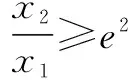
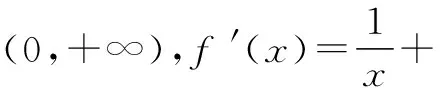
(1)a≥0时,f′(x)>0,∴f(x)在(0,+∞)上单调增；

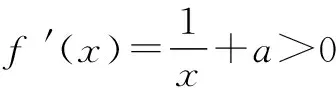
(2) ∵lnx1+ax1=0,lnx2+ax2=0,∴lnx2-lnx1=a(x1-x2).

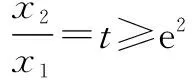
评注 利用放缩法在求解导数问题时一直扮演着较难的角色.在导数中的放缩可根据最值点进行放缩，这时题目一般会将函数设置为在某区间的单调函数.

六、数学思想的综合证法

例题6 (2016年福建省宁德质检)已知函数f(x)=(x-k-1)ex．

(1)当x>0时，求f(x)的单调区间和极值；

(2)若x1≠x2，且f(x1)=f(x2)，证明：x1+x2<2k．

解析 (1)f′(x)=(x-k)ex,x>0.(ⅰ)当k≤0时，f′(x)>0恒成立,∴f(x)的递增区间是(0，+∞)，无递减区间,无极值. (ⅱ)当k>0时，由f′(x)>0,得x>k,由f′(x)<0得0

(2)由已知f(x1)=f(x2)(x1≠x2)，结合(Ⅰ)可知k>0,f(x)在(-∞,k)上单调递减，在(k,+∞)上单调递增.又f(k+1)=0，xk，2k-x1>k，故要证x1+x2<2k，只要证2k-x1>x2，只要证f(2k-x1)>f(x2).因f(x1)=f(x2)，即证f(2k-x1)>f(x1).

评注 本题主要考查化归与转化思想、函数与方程的思想、分类整合思想、数形结合思想．综合了函数、导数、不等式等基本知识；考查运算求解能力、推理论证能力.因此在解决这类综合性导数问题，如果能够利用数学思想对问题分析求解将会大大降低求解难度.

在求解导数压轴题时，需要在平时的基础上善于总结发现解题规律，才能以不变应万变来求解导数证明问题.善于利用数学思想去解决数学问题将会提高数学的解题能力和速度，因此在学习过程中要善于运用数学思想去求解各类问题.

G632

B

1008-0333(2016)34-0014-02