复杂地层盾构掘进速率和刀盘扭矩预测模型及其地层适应性研究

张志奇， 李 彤， 韩爱民， 苏 明， 黄新强

(1. 中交隧道工程局有限公司， 北京 100088； 2. 南京工业大学岩土工程研究所， 江苏 南京 210000；3. 江苏省岩土工程公司， 江苏 南京 210000)

复杂地层盾构掘进速率和刀盘扭矩预测模型及其地层适应性研究

张志奇1， 李 彤2,3,*， 韩爱民2， 苏 明1， 黄新强3

(1. 中交隧道工程局有限公司， 北京 100088； 2. 南京工业大学岩土工程研究所， 江苏 南京 210000；3. 江苏省岩土工程公司， 江苏 南京 210000)

以复杂地层地质分段为基础，统计不同地质分段的盾构掘进参数，开展针对盾构掘进速率与刀盘扭矩的多元回归分析，得到适用于复杂地层的掘进参数回归模型，并分析回归模型系数与全断面等效岩体基本质量指标间的相关性。研究表明： 全断面等效岩体基本质量指标考虑了复杂地层中不同区段掌子面内各地层面积占比差异，可作为地质分段标准； 掘进速率与刀盘扭矩的回归预测值与实测值间相对误差较小，回归模型对均质地层及复合地层均有较好的拟合精度； 围岩等级提高时，掘进速率、刀盘扭矩回归模型系数具有明显的分段变化特征。其量化结论可用于定量预测不同地层盾构掘进参数，以提高盾构施工效率。

盾构； 复杂地层； 掘进参数； 回归模型； 地层适应性

0 引言

盾构掘进过程中，掘进速率决定着工期，是进度计划与全工期成本控制的关键。刀盘扭矩表征滚刀破岩时所受的冲击荷载，可通过分析其摩擦比例因数波动程度推测刀具工作状态与磨损情况[1]，是合理提高刀具破岩效率、减少开舱检查及换刀所需时间的重要控制指标。复杂地层中，均质地层与复合地层逐段分布，盾构掘进沿线地层物理、力学参数逐段相异，寻找适用于复杂地层的盾构掘进速率、刀盘扭矩的预测方法，对盾构掘进施工具有一定的理论指导意义和参考价值。

目前，盾构掘进速率、刀盘扭矩的预测方法主要有理论计算法与经验预测法。理论计算法中，L.Ozdemir等[2]以单具滚刀受力分析为基础，建立CSM模型，预测刀盘扭矩、掘进速率等参数； 王洪新等[3]建立了盾构掘进几何连续性方程、物理方程及平衡方程，结合对盾构施工参数记录的回归分析，验证了各掘进参数间的关系； 管会生等[4]建立了由切削、摩擦产生的刀盘扭矩理论方程，并分析上海、成都地铁施工刀盘扭矩组成的差异； 李潮等[5]推导了刀盘扭矩7个组成部分的计算模型，结合工程实践，分析了刀盘扭矩各影响因素的敏感性。经验预测法中，N.Barton[6]在岩体质量指标Q基础上引入掘进参数，形成QTBM模型，用于预测掘进速率;A.Bruland[7]以盾构施工参数数据库为基础，结合岩石脆性试验、磨损试验等室内试验，建立NTNU模型,预测掘进速率等掘进参数;张厚美等[8]、宋克志等[9]和李青松等[10]通过对既有施工数据进行回归计算，得到掘进速率、刀盘扭矩与其他掘进参数、地质因素等影响因素间的经验关系。

理论计算模型中，关键参数的选取决定了预测结果的精度，需由特定试验获取，在复杂地层的工程应用中存在局限。QTBM模型参数过多，影响其工程应用； NTNU模型不适用于坚硬但完整性较差的地层； 而文献[8-10]中回归预测模型针对均质地层或某种复合地层，缺少回归模型在复杂地层中的适应性分析。为提高复杂地层掘进参数的预测精度，以掌子面全断面等效岩体基本质量指标为基础，对复杂地层进行地质分段，分段统计掘进参数。通过逐步回归计算掘进速率、刀盘扭矩与其他掘进参数间的经验关系，得到适用于均质地层、复合地层的掘进速率、刀盘扭矩回归模型，并讨论回归模型在盾构掘进施工中的具体应用。通过定量分析回归模型系数在掌子面全断面等效岩体基本质量指标升高时的分段变化规律，研究掘进速率、刀盘扭矩回归模型的地层适用性。

1 工程概况

1.1 工程地质条件

南京市宁高城际轨道交通二期工程盾构隧道区间段全长2 390 m，其中68.8%的区间穿越中风化安山岩，其余区间主要穿越由黏性土、砂土、强风化安山岩和中风化安山岩构成的复合地层。盾构段各地层性质如下。

1)混合土(③-4)。灰黄色，软—可塑，主要成分为细中砂、粗砂、混砂砾土，砂为中密—密实，局部为粉质黏土。

2)残积土(④)。棕红色，可塑—硬塑，以黏性土为主，夹风化岩屑。

3)强风化安山岩(J31-2)。砂土状，夹少量中风化岩块，岩体基本质量等级为V级。

4)中风化安山岩(J31-3r)。饱和单轴抗压强度平均值为19.38 MPa，岩体完整性指数为0.50。

5)中风化安山岩(J31-3p)。饱和单轴抗压强度平均值为45.95 MPa，岩体完整性指数为0.32。

6)中风化安山岩(J31-3)。饱和单轴抗压强度平均值为63.35 MPa，岩体完整性指数为0.59。

项目采用海瑞克复合式土压平衡盾构，刀盘直径6 480 mm，最大推力42 575 kN，最大推进速率80 mm/min，脱困扭矩7 476 kN·m。

刀盘采用“4辐条+4面板”形式，开口率为36%。配备中心滚刀8把，正面滚刀24把，边缘滚刀13把。滚刀带有高度耐磨的合金齿切削环，刀圈直径17 in。

1.2 地质分段与掘进参数分段统计

盾构区间沿线地质条件复杂多变，掘进地层多为复合地层，由多种岩层、土层组成，而全断面各层组成比例在一定掘进方向范围内变化较小，具备地质分段条件。地质剖面中地层分界线与隧道轴线间夹角越小，隧道掌子面内各地层比例在掘进方向上变化越小，掘进范围内地层条件变化越小，掌子面内某地层断面面积变化越小。根据地勘报告，将隧道穿越地层组成相同且地质纵断面中地层分界线与隧道轴线近似平行的部分归为同一地质分段，定义该地质分段全断面等效岩体基本质量指标

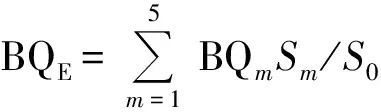
(1)

式中：S0为掌子面全断面面积； BQm和Sm分别为掌子面内某地层的岩体基本质量指标和断面面积。

隧道掌子面内各地层划分方法如图1所示。不同地质分段掌子面内各地层断面面积相异使掌子面BQE不同，导致不同地质分段掌子面与刀盘间的相互作用、掘进参数间的相互关系存在差异。其中，各地层BQm根据文献[11]计算，各地质分段BQE计算结果见表1。

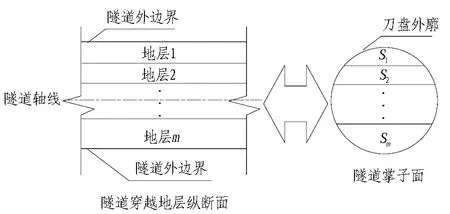
图1 隧道掌子面内各地层划分方法

盾构掘进系统由PLC电路采集信号，控制室主机系统记录盾构掘进速率、刀盘转速、总推力、铰接阻力、扭矩、土舱压力等参数，生成每环内各参数的平均值报表。以地质分段为基础，统计隧道沿线各段掘进参数，作为回归分析样本。

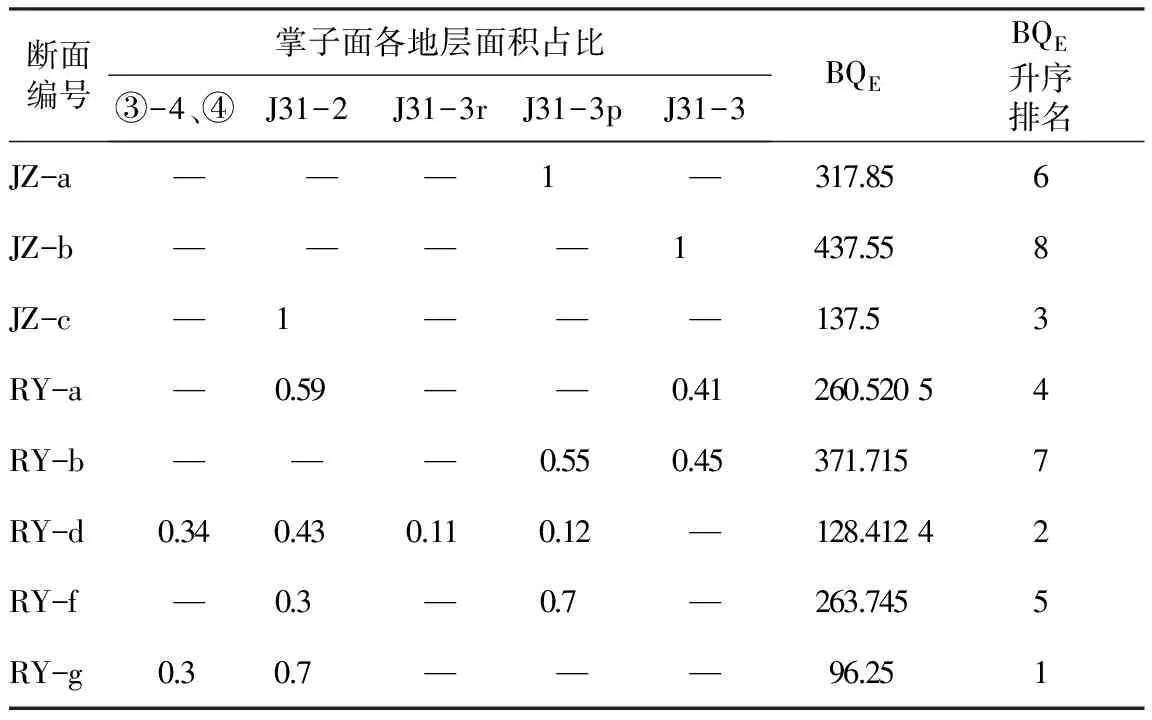
表1 盾构穿越地层掌子面分段统计

注： JZ表示均质地层； RY表示上软下硬复合地层。

2 掘进参数回归分析

2.1 推进速率回归模型

工程实践表明，掘进过程中掘进速率、刀盘扭矩与其他掘进参数间存在非线性数学关系[12]。8组地质分段均由上百乃至数百环构成，盾构记录每环的掘进参数。对于某地质分段(某断面)，回归分析的样本是构成地质分段的上百或数百环掘进参数。以JZ-c地层为例，该地质分段包含右线910—990环及左线950—1 025环，共157环。根据157环的157组掘进参数得到157组样本，进行回归分析，得到属于JZ-c地层的掘进速率回归模型系数(li，i=1,2,3，…,8)及刀盘扭矩回归模型系数(kj，j=1,2,3,…,7)。8组地质分段(8种断面)的掘进速率、刀盘扭矩回归模型均如此得出，样本量均达到上百乃至数百组，相对2种模型的自变量个数而言，样本数量满足回归分析要求。

针对8组地质分段，分别将各地质分段基本自变量(掘进参数一次幂F、p、n)及其若干次幂作为元素集进行元素集间笛卡尔乘积运算，得到属于各地质分段的单项变量及二元复合变量集合，作为多元回归分析的自变量集。利用SPSS统计计算软件进行多元逐步线性回归运算，得到分别独立属于8组地质分段的掘进速率回归模型。按照共性提升原则，将8组地质分段的掘进速率回归模型中相同的自变量抽出来，将它们线性组合形成预测不同地层掘进速率的通式，作为复杂地层掘进速率回归模型，见式(2)及式(3)。

vf=l1n+l2F+l3p+l4p3+l5F1/3+l6Fp+l7n1/2F+l8。

(2)

F=Ft-Fh。

(3)

式(2)和式(3)中：vf为掘进速率拟合值，mm/min；n为刀盘转速，r/min；Ft为总推力，kN；Fh为铰接阻力，kN；p为土舱压力，0.1 MPa；F为总推力与铰接阻力之差，即刀盘与掌子面间掘进方向作用力,kN；li(i=1,2,3，…,8)为掘进速率回归模型系数。

8组地质分段掘进速率回归模型系数见表2。在各地层中式(2)均具有一定的拟合精度，对均质地层、复合地层同时适用，具有一定程度的普适性。均质地层与复合地层的掘进速率多元回归拟合值与实测值对比如图2和图3所示(分别以JZ-c地层、RY-a地层为例)。

各分段掘进速率回归模型自变量显著性如图4所示。8组地质分段的掘进速率回归模型中，RY-a中p3、RY-b中p3及F1/3、JZ-c中Fp的显著性大于0.05，JZ-c中F的显著性大于0.1。各地质分段的掘进速率回归模型均拥有8个自变量，在8组地质分段范畴内，自变量对0.05显著性水平(sig.v)的合格率为92.18%，对0.1显著性水平的合格率为98.44%，该回归模型在均质地层与复合地层掘进速率预测中均具有统计意义。

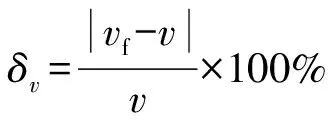
(4)

式中：δv为掘进速率回归预测的相对误差；vf为掘进速率拟合值；v为掘进速率实测值。

8组地质分段的回归预测平均相对误差均小于37.0%，其中7组平均相对误差介于10%～ 20%，表明掘进速率回归模型在复杂多变的地质条件下具有较高的预测精度。

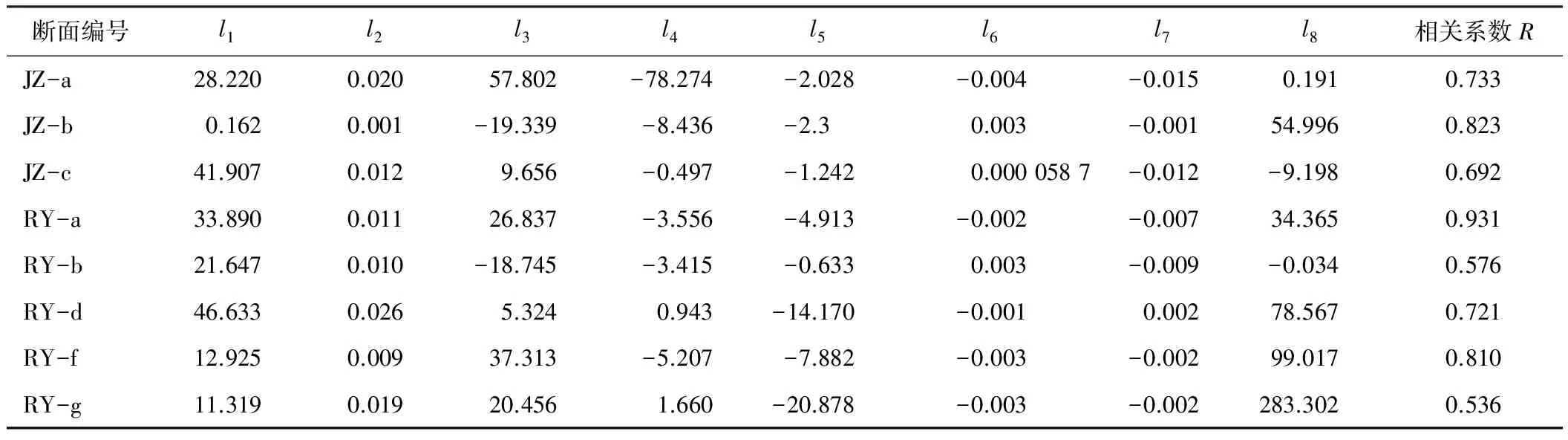
表2 各分段盾构掘进速率回归模型系数

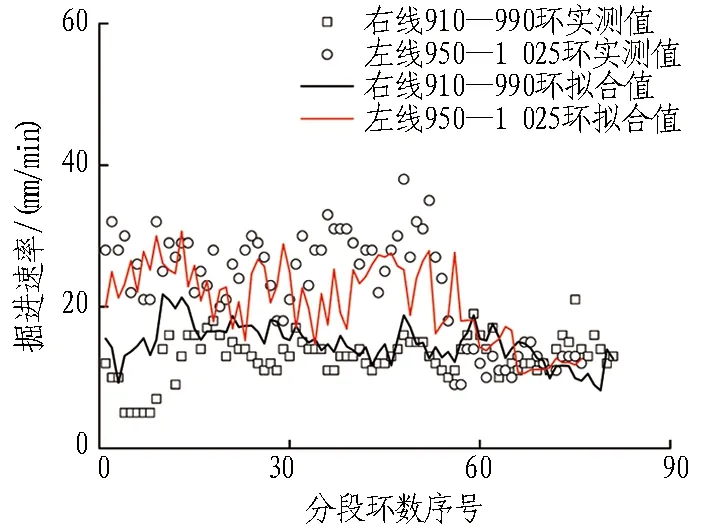
图2 均质地层掘进速率拟合结果(JZ-c地层)

Fig. 2 Fitting results of shield advancing speed in homogeneous stratum (JZ-c strata)

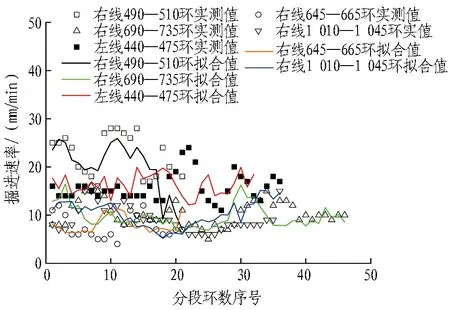
图3 复合地层掘进速率拟合结果(RY-a地层)

Fig. 3 Fitting results of shield advancing speed in complex strata(RY-a strata)

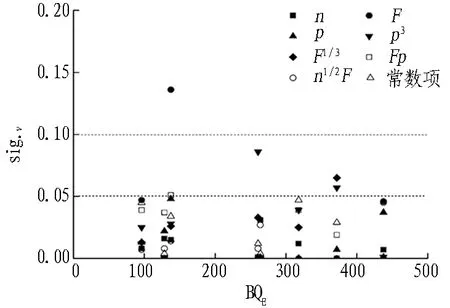
图4 各分段掘进速率回归模型自变量显著性

Fig. 4 Significances of every independent variable of regression model of shield advancing speed

掘进速率与刀盘转速、推力成正比，与花岗岩残积土和全风化花岗岩复合地层掘进经验[10]相似。土舱压力与掘进速率的相关性呈现明显的分段特征，土舱压力与掘进速率由正相关转向负相关的掌子面临界BQE值域为(317.85, 371.715)，即在强度较低、完整性较差的地层中，增大土舱压力有利于保持掌子面稳定； 同时，注入的泡沫剂改善了渣土的流动性，有利于防止螺旋输送机出渣喷涌，可以有效提高掘进速率。在强度和完整性较高的地层中，盾构所受阻力较大、掘进速率较低，应当降低土舱压力，提高有效推力。渣土颗粒体积较大、质量较大，须加大泡沫剂用量，以降低渣土颗粒输送时对刀盘、刀具的二次磨损[13]，并延长螺旋输送机使用寿命[14]，即土舱压力及其幂与掘进速率呈负相关。

2.2 刀盘扭矩回归模型

刀盘扭矩回归模型的推导方法与掘进速率回归模型相同。预测不同地层刀盘扭矩的通式，即刀盘扭矩回归模型

Tf=k1n+k2F+k3p+k4p3+k5n2p1/3+k6F1/2+k7。

(5)

式中：Tf为刀盘扭矩拟合值，MN·m；n为刀盘转速，r/min；p为土舱压力，0.1 MPa；F为总推力与铰接阻力之差，即刀盘与掌子面间掘进方向作用力，kN；kj(j=1,2,3,…,7)为刀盘扭矩回归模型系数。

8组地质分段刀盘扭矩回归模型系数见表3。在各地层中式(5)均具有一定的拟合精度，对均质地层和复合地层同时适用，具有一定程度的普适性。均质地层与复合地层的掘进速率多元回归拟合值与实测值对比如图5和图6所示(分别以JZ-c地层、RY-a地层为例)。

各分段刀盘扭矩回归模型自变量显著性如图7所示。8组地质分段的刀盘扭矩回归模型中，RY-g中n2p1/3、JZ-a中F1/2、RY-d中常数项、JZ-b中n的显著性大于0.05，RY-d中p的显著性大于0.1。各地质分段的刀盘扭矩回归模型均拥有7个自变量，在8组地质分段范畴内，自变量对0.05显著性水平(sig.T)的合格率为91.07%，对0.1显著性水平的合格率为96.43%，该回归模型在均质地层与复合地层刀盘扭矩预测中均具有统计意义。

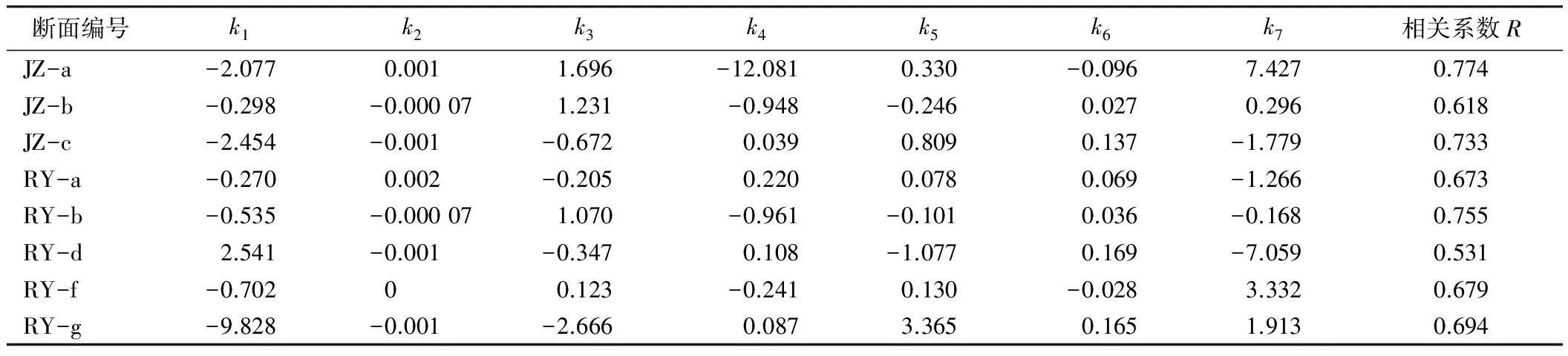
表3 各分段盾构刀盘扭矩回归模型系数

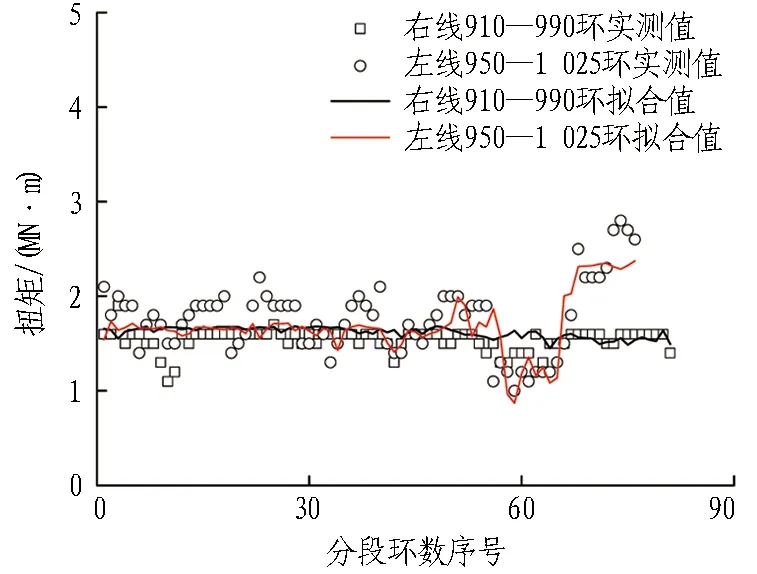
图5 均质地层刀盘扭矩拟合结果(JZ-c地层)

Fig. 5 Fitting results of cutterhead torque in homogeneous stratum(JZ-c strata)

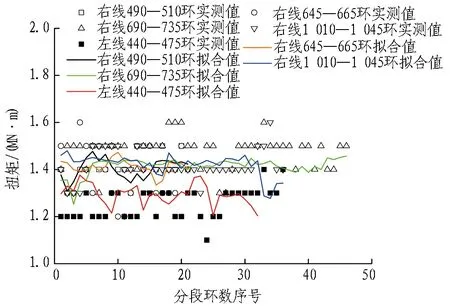
图6 复合地层刀盘扭矩拟合结果(RY-a地层)

Fig. 6 Fitting results of cutterhead torque in complex strata (RY-a strata)

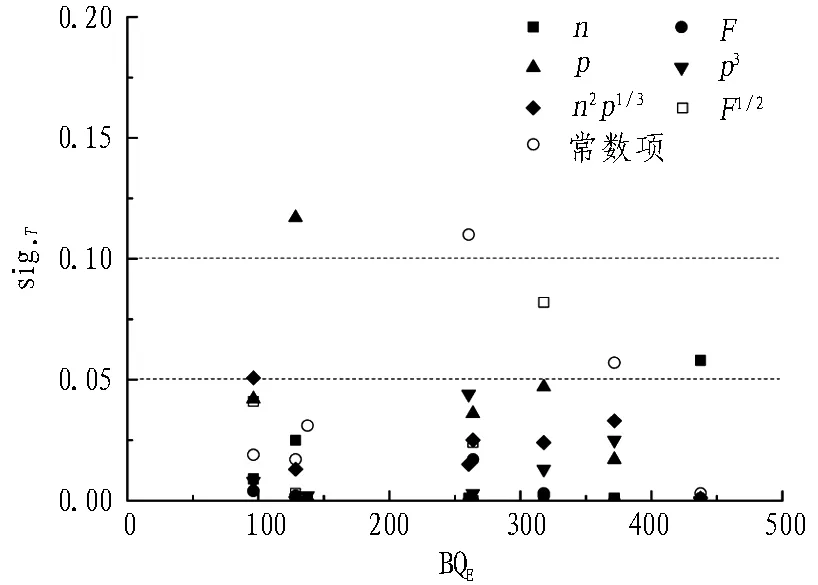
图7 各分段刀盘扭矩回归模型自变量显著性

Fig. 7 Significances of every independent variable of regression model of cutterhead torque

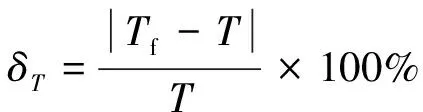
(6)

式中：δT为刀盘扭矩回归预测的相对误差；Tf为刀盘扭矩拟合值；T为刀盘扭矩实测值。

8组地质分段的回归预测平均相对误差均小于25.0%，其中7组平均相对误差介于0～20%，表明掘进速率回归模型对均质地层及上软下硬地层均具有较好的预测精度。

盾构掘进过程中，扭矩控制是保证液压、电机设备正常工作，不超负荷，降低滚刀非正常磨损，避免轴承、刀座发生损坏的关键，主要通过增减推力和刀盘转速来实现。为保证持续、安全掘进，通常设置扭矩警戒值作为施工控制指标。当扭矩增大时，应降低刀盘转速或降低推力。回归分析以既有掘进参数为基础。由表3可知，8组地质分段扭矩回归模型的k1与k2、k6均互为正负异号或同为负值，是基于扭矩警戒值的人工干预在回归分析中的体现。反之，掘进过程中若出现k1与k2、k6均为正值的情况，说明在该段掘进中盾构操作人员未能在刀盘扭矩增大时通过降低刀盘转速和推力以控制刀盘扭矩增大的趋势，可能会导致刀盘、刀具、液压、机电设备的异常损耗或失效。刀盘扭矩回归模型在反映掘进过程中各盾构状态参数间相互关系的同时，还能够作为判断盾构操作人工干预力度、设备运转及损耗状况的有效手段。

2.3 回归模型地层适应性分析

掌子面地层组成不同时，刀具、刀盘在掘进中与地层的相互作用力存在差异，导致掘进速率、刀盘扭矩的回归方程系数存在差异。利用式(7)及式(8)分别计算不同地质分段掘进速率、刀盘扭矩回归方程系数的离均差率(Mean Deviation Rate, MDR)MDRv、MDRT。

(7)

(8)

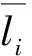
掘进速率和刀盘扭矩回归方程系数离均差率计算结果如图8和图9所示。

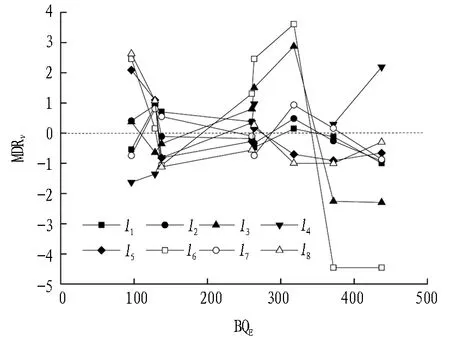
图8 掘进速率回归方程系数离均差率

Fig. 8 Mean deviation rate of coefficients of regression model of shield advancing speed

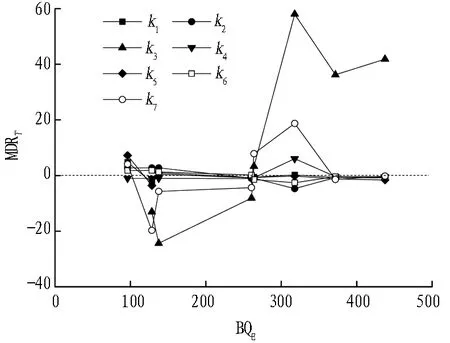
图9 刀盘扭矩回归方程系数离均差率

Fig. 9 Mean deviation rate of coefficients of regression model of cutterhead torque

由图8和图9可知，当掌子面BQE增大时，掘进速率、刀盘扭矩回归模型系数li、kj的变化趋势存在明显的分段特征。掌子面BQE在(100，150)内时，li对其平均值的偏离程度均逐渐减小，MDRv逐渐收敛于(-1,1)；除k7外，kj对其平均值的偏离程度均逐渐减小，且k1、k2、k4、k5、k6的MDRT逐渐收敛于(-3,1)。掌子面BQE在(150，250)内时，MDRv、MDRT主要在(-1，1)、(-3,1)内波动，掘进速率、刀盘扭矩回归模型各系数均变化较小，地层变化对各掘进参数间关系的影响较小。掌子面BQE在(250，350)内时，li、kj对其平均值的偏离程度均先增大后减小，除l3、l6、k3外，其他系数的MDRv、MDRT分别最终收敛于(-1，1)、(-2，0)内，回归模型各系数均变化剧烈，地层变化对各掘进参数间关系的影响较为显著。掌子面BQE大于350时，各系数趋于定值或有限波动，表明在掘进地层强度、完整性较高时，岩体质量的提高对回归模型系数的影响较小，受刀具材料性能及液压、机电设备负载极限所约束，掘进速率、刀盘扭矩均达到或接近极限值，此时应限制其他控制参数波动，以减少盾构所受冲击荷载，保障盾构高效、稳定地掘进。

3 结论与讨论

1)全断面等效岩体基本质量指标反映了掌子面内各地层面积占比差异，能够量化复合地层围岩物理、力学性质差异，可作为复杂地质条件下的地质分段与掘进参数预测的基础。

2)掘进速率与刀盘扭矩回归预测模型的自变量对0.05显著性水平的合格率均高于90%，表明回归模型对不同地层具有较高的普适性。预测值与实测值间的相对误差多集中在0～20%，表明回归模型对均质地层及复合地层均有较好的拟合精度。

3)掘进速率与刀盘转速、推力成正比。掘进速率与土舱压力的相关性呈现明显的分段特征，相应的掌子面临界BQE值域为(317.85, 371.715)，掌子面BQE位于临界值域两侧地层的土舱压力控制措施相反。

4)掌子面BQE提高时，以150、250为临界值，掘进速率、刀盘扭矩回归模型系数对其平均值的偏离程度分段变化，地层变化对各掘进参数间关系的影响先减小后增大；掌子面BQE高于350时，回归模型系数变化趋于稳定，地层变化对各掘进参数间关系的影响较小。

复杂地层盾构掘进速率和刀盘扭矩预测模型是对既有施工参数的统计学分析结果，能够逼近变量间的客观数学规律，但无法完全揭示研究对象间的物理规律。预测模型在各地层中均具有一定的拟合精度，但并未达到对掘进速率和刀盘扭矩的完全精准预测，仍有改进和提高的空间。

[1] 左翠凤, 唐德高, 戎晓力, 等. 基于刀盘摩擦扭矩参数的刀具磨损状态识别[J]. 隧道建设, 2016, 36(3): 344-348.(ZUO Cuifeng, TANG Degao, RONG Xiaoli, et al. State recognition of cutter wear based on frictional torque parameters of cutterhead[J]. Tunnel Construction, 2016, 36(3): 344-348. (in Chinese))

[2] Ozdemir L, Miller R, WANG F D. Mechanical tunnel boring-prediction and machine design[R]. Colorado: Colorado School of Mines, 1977.

[3] 王洪新, 傅德明. 土压平衡盾构掘进的数学物理模型及各参数间关系研究[J]. 土木工程学报, 2006, 39(9): 86-90.(WANG Hongxin, FU Deming. A mathematical model and the related parameters for EPB shield tunneling[J]. China Civil Engineering Journal, 2006, 39(9): 86-90. (in Chinese))

[4] 管会生, 高波. 盾构刀盘扭矩估算的理论模型[J]. 西南交通大学学报, 2008, 43(2): 213-217.(GUAN Huisheng, GAO Bo. Theoretical model for estimation of cutter head torque in shield tunneling[J]. Journal of Southwest Jiaotong University, 2008, 43(2): 213-217.(in Chinese))

[5] 李潮, 周宏伟, 左建平, 等. 土压平衡盾构刀盘扭矩计算方法与多因素量化分析[J]. 岩石力学与工程学报, 2013, 32(4): 760-766.(LI Chao, ZHOU Hongwei, ZUO Jianping, et al. Torque calculation method of cutterhead in earth pressure balance shield and quantitative analysis of several influencing factors[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(4): 760-766. (in Chinese))

[6]Barton N. TBM performance estimation in rock using Q(TBM)[J]. Tunnels & Tunnelling International, 1999, 31(9): 30-34.

[7] Bruland A. Hard rock tunnel boring[D]. Trondheim: Norwegian University of Science and Technology, 2000.

[8] 张厚美, 吴秀国, 曾伟华. 土压平衡式盾构掘进试验及掘进数学模型研究[J]. 岩石力学与工程学报, 2005(增刊2): 5762-5766.(ZHANG Houmei， WU Xiuguo， ZENG Weihua. Study of tunneling experiment and mathematical model of EPB shield[J]. Chinese Journal of Rock Mechanics and Engineering, 2005(S2): 5762-5766. (in Chinese))

[9] 宋克志, 杨华勋, 安凯, 等. 复杂岩石地层盾构掘进速率预测模型研究[J]. 公路交通科技, 2008, 25(11): 105-108.(SONG Kezhi, YANG Huaxun, AN Kai, et al. Shield tunneling rate prediction model for complex rock stratum [J]. Journal of Highway and Transportation Research and Development, 2008, 25(11): 105-108. (in Chinese))

[10] 李青松, 石豫川, 周春宏. 多元回归法在某水电站TBM施工隧洞围岩质量预测中的应用[J]. 长江科学院院报, 2012, 29(2): 41-45.(LI Qingsong, SHI Yuchuan, ZHOU Chunhong. Application of multiple regression method to the prediction of surrounding rockmass quality for TBM-excavated tunnels of hydropower station[J]. Journal of Yangtze River Scientific Research Institute, 2012, 29(2): 41-45. (in Chinese))

[11] 工程岩体分级标准: GB/T 50218—2014[S]. 北京: 中国计划出版社, 2014: 8-9. (Standard for engineering classification of rock mass: GB/T 50218—2014[S]. Beijing: China Planning Press, 2014: 8-9. (in Chinese))

[12] 周斌, 张怀亮, 程永亮. 复合地层盾构机推进速度SVM预测模型研究[J]. 铁道建筑技术, 2014(10): 48-51. (ZHOU Bin, ZHANG Huailiang, CHENG Yongliang. Research on SVM prediction model of shield speed in the complex stratum[J]. Railway Construction Technology, 2014(10): 48-51. (in Chinese))

[13] 张厚美. TBM盘形滚刀重复破碎与二次磨损规律研究[J]. 隧道建设, 2016, 36(2): 131-136.(ZHANG Houmei. Study of relationship between repeated cutting and secondary wear of TBM disc cutter[J]. Tunnel Construction, 2016, 36(2): 131-136. (in Chinese))

[14] 王树华. 成都砂、卵石地层盾构机耐磨性及刀具适用性研究[J]. 隧道建设, 2012, 32(1): 11-18.(WANG Shuhua. Study of wearing-resistant capacity and cutting tool adaptability of shield machine: Machines used in sandy gravel stratum in Chengdu[J]. Tunnel Construction, 2012, 32(1): 11-18.(in Chinese))

Prediction Models of Advancing Speed and Cutterhead Torque of Shield Tunneling in Complex Strata and Its Adaptability to Strata

ZHANG Zhiqi1, LI Tong2, 3, *, HAN Aimin2, SU Ming1, HUANG Xinqiang3

(1. CCCC Tunnel Engineering Company Limited, Beijing 100088, China; 2. Institute of Geotechnical Engineering,NanjingTechUniversity,Nanjing210000,Jiangsu,China; 3.GeotechnicalEngineeringCompanyofJiangsuProvince,Nanjing210000,Jiangsu,China)

In this paper, the shield tunneling parameters in different geological sections are summarized; the multiple regression analysis is made on advancing speed and cutterhead torque of shield; the regression model of shield tunneling parameters in complex strata is obtained; and the relationship between parameters of regression models and the full-face equivalent basic quality index of rock mass is studied. The study results show that: 1) The full-face equivalent basic quality index of rock mass with consideration of proportion of different geological conditions can take as standards for geological sectioning. 2) The difference between predicted advancing speed and cutterhead torque of shield and measured data is little. The regression models have a good adaptability to homogeneous or complex strata. 3) The parameters of regression models, shield advancing speed and cutterhead torque, have obvious sectioned characteristics when the surrounding rock grade increases. The quantified results can be applied to predict shield advancing parameters in different strata and improve shield tunneling efficiency.

shield; complex strata; tunneling parameters; regression model; adaptability to strata

2016-04-12;

2016-06-20

中交隧道局重点科研项目(SDKJ2014-005)

张志奇(1985—)，男，黑龙江齐齐哈尔人，2007年毕业于北京机械工业学院，测控技术与仪器专业，本科，工程师，现主要从事盾构施工技术和生产管理工作。E-mail： 249525836@qq.com。*通讯作者： 李彤， E-mail： gnotil80@163.com。

10.3973/j.issn.1672-741X.2016.12.007

U 455

A

1672-741X(2016)12-1449-07