基于多特征融合多核学习支持向量机的液压泵故障识别方法

刘志强 姜万录 谭文振 朱 勇

1.燕山大学河北省重型机械流体动力传输与控制重点实验室,秦皇岛,0660042.先进锻压成形技术与科学教育部重点实验室,秦皇岛,0660043.唐钢高强汽车板有限公司,唐山,063002

基于多特征融合多核学习支持向量机的液压泵故障识别方法

刘志强1,2,3姜万录1,2谭文振3朱 勇1,2

1.燕山大学河北省重型机械流体动力传输与控制重点实验室,秦皇岛,0660042.先进锻压成形技术与科学教育部重点实验室,秦皇岛,0660043.唐钢高强汽车板有限公司,唐山,063002

提出基于多特征融合多核学习支持向量机的液压泵故障识别方法。该方法首先对原始信号进行集总经验模态分解，然后分别用AR模型和奇异值分解两种特征提取方法提取故障特征，最后将不同类型的特征分别用相应的核函数进行映射，用多核学习支持向量机来识别液压泵的工作状态和故障类型。实验结果表明该方法显著地提高了故障诊断的准确性。

多核学习;多特征融合;支持向量机;故障识别;液压泵

0 引言

作为液压系统的核心部件，液压泵的工作状态严重影响着液压系统工作的可靠性。目前，与统计分类器和神经网络分类器对应的统计模式识别方法和神经网络方法是用于液压泵模式识别的主要方法，而这些方法都存在许多固有的局限性。基于统计学习理论发展起来的支持向量机(support vector machine，SVM)在有限样本的条件下有效地解决了小样本、非线性、局部极小点和高维数等工程实际难题。但是SVM采用的是对所有样本进行统一处理的单核映射方法，核函数的类型对支持向量机的推广能力有重要影响，因此与实际问题相适应的核函数的选择和构造一直是支持向量机研究领域的重要课题。同时，SVM也不适合处理样本规模很大、数据维数高或数据在高维特征空间分布不平坦等情况下的学习问题[1]。另外，由于单核函数的格式固定且变化空间相对狭小，训练后的有效参数仍然对样本数据有较强的敏感性，所以推广能力和鲁棒性较差[2]。对于以上问题，近几年关于多核学习(multiple kernel learning，MKL)方法的研究广受关注。相关研究表明[3-9]，多核模型有比单核模型更优良的分类性能，并能增强分类函数的可解释性。应用多个基本核函数的凸组合是构造多核模型最常用的一种方法。多核学习把如何描述样本映射到特征空间的问题转化为如何选择基本核与权系数的问题。由于组合核能够利用各基本核函数的特性，弥补单个核函数的不足，因此多核学习方法是解决以上问题的一条有效途径。

液压泵的故障信号十分复杂，常表现出明显的非线性、非平稳性。虽然小波和小波包分析、Wigner-Ville分布、短时傅里叶变换(STFT)等方法都能够对该类型信号的时频复杂性进行一定程度的恰当刻画，但都存在各自的局限性[10]。经验模态分解(empirical mode decomposition，EMD)是由Huang等[11]提出的一种信号处理方法，该方法能把复杂的信号分解成若干个固有模态分量(intrinsic mode function，IMF)之和，能根据被分析信号的不同，自适应地选择特征尺度(频带)，因此解决了传统包络分析中的难题，即需要根据经验预先确定滤波器的中心频率和带宽。但EMD算法存在的模态混淆效应会对故障识别造成负面影响。作为对EMD算法的一个重大改进，集总经验模态分解(ensemble empirical mode decomposition，EEMD)方法是Wu等[12]提出的一种能够有效抑制模态混淆，刻画信号本质特征的新方法。

本文将AR(auto regressive)模型[13]和奇异值分解[14]两种特征提取方法进行融合，用多核学习方法有效地组合不同特征和不同核，将特征向量中的不同特征分量分别用对应的核函数进行映射，使不同类别的样本在新特征空间中的区分性更明显；同时将EEMD方法应用到液压泵振动信号的处理上，为特征提取和模式识别构造良好的数据源；采用多核学习方法有效地组合不同特征和不同核，以期更好地揭示故障本质，提高液压泵故障诊断的准确率。

1 振动信号特征提取

1.1 集总经验模态分解

EEMD是在待分析信号中多次叠加高斯白噪声，对多个加噪后的信号分别进行EMD分解后求平均的一种模态分解方法。由于高斯白噪声具有频率均匀分布的统计特性，故可利用这一特性使加入噪声后的信号在不同尺度上连续，从而有效抑制模态混淆问题。EEMD的提出基于以下两个观点：

(1) 在多次分解中叠加的同等幅值水平的随机高斯白噪声可以相互抵消，即经过多次加噪分解后作为平均结果保留的是所分析信号的原始成分。

(2) 在原始信号上叠加随机白噪声可以改变信号原有的时间尺度，多次叠加不同的白噪声就能使EMD根据信号的变化自适应地重新分解信号，这样经过综合平均后得到的IMF能更全面、更客观地体现信号中各组分的信息。

EEMD算法流程如图1所示，详细实现步骤参见文献[12]。

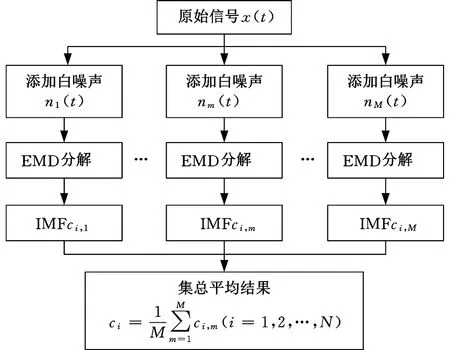
图1 EEMD算法流程图

1.2 AR模型提取故障特征

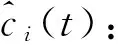
(1)

(2)

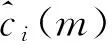
在确定模型阶数p时，用定阶准则确定的不同IMF分量的阶数可能不同，由于各个样本的特征向量的维数要求相同，所以本文首先采用FPE准则(final prediction error criterion)确定各个IMF分量的AR模型的阶数范围，最后选定各个IMF分量AR模型的阶数为30。

1.3 奇异值分解提取故障特征

针对液压泵的特征提取，首先对液压泵每个振动信号样本xi(t)进行EEMD分解，将得到的N个IMF分量(c1，c2，…，cN)组成如下的初始特征矩阵：

A=[c1c2… cN]T

(3)

为了得到原始振动信号的奇异值特征，需要对初始特征矩阵A进行奇异值分解。

根据矩阵理论，作为矩阵的固有特征，矩阵的奇异值不但具有良好的稳定性，还具有旋转不变性和比例不变性。矩阵奇异值的这些特征符合模式识别中对模式特征的稳定性及旋转、比例不变性的要求[14]，因此可以把初始特征矩阵的奇异值作为故障特征，用于旋转机械的状态识别。矩阵奇异值的计算过程参见文献[14]。

2 多核学习支持向量机方法

在多核学习方法中，克服传统单核函数固有缺陷的一种有效的方法就是用多个基本核函数的凸组合来代替传统的单一核函数[15]。

2.1 多核学习支持向量机模型

已知{xi,yi|i=1,2,…，n}为学习机器的数据集，xi为输入空间X中的样本，yi为xi的目标值。对于核方法，学习问题结果表达式的形式如下：

(4)

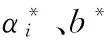
近年来的理论和应用表明，使用多核来代替单核可以提高决策函数的可解释性，能够获得比单核模型更优的性能。多核函数表达式为

(5)

其中，M为基核的数目，dm为第m个基核函数对应的权值，Km(xi,x)为基核。每个基核函数Km(xi,x)可以使用样本x的所有指标，也可以使用样本x的部分指标。基核函数可分别选取不同类型的核函数和同一类型不同自由参数的核函数。例如可以选取径向基核函数和多项式核函数进行组合，还可以选取一组不同宽度的径向基函数。学习机器经过学习训练，可以得到最优的权值。在这样的框架下，通过核函数进行数据表示的问题就转化为权系数dm的选择问题。

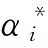
(6)

式中，C为规则化参数；ξi为松弛变量。

(7)

d=(d1,d2，…,dM)

2.2 多核学习问题求解算法

式(7)可视为如下问题进行求解：

(8)

(9)

值得注意的是目标函数J(d)实际上是标准SVM的目标值。

式(9)的拉格朗日函数为

(10)

其中，αi、νi为拉格朗日乘子，αi≥0，νi≥0。式(12)对变量求偏导，并令它们等于0，有

(11)

将这些最优化的条件代入到拉格朗日方程式(10)，得到对偶表达式：

(12)

(13)

其中α*是求解最优化问题式(12)得到的α的最优解。其中，目标值J(d)可以通过任何一个标准SVM算法求得。

将对偶表达式式(12)对dm求偏导，有

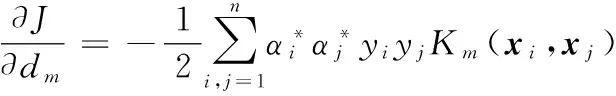
(14)

式(8)所示的优化问题是由一个非线性的目标函数和一个简单的限制条件组成的。在SimpleMKL算法中用梯度下降[7,15]的方法解决此问题。

3 多特征的组合方法

特征组合方法以传统的二分类问题为基础，在训练样本上增加了标注特征的标志。给定一个训练样本集Ω，它包含了n个样本，每个样本有M种特征描述：

(15)

其中，yi为第i个样本的分类类型。由M类特征组成的样本xi中，xi,m定义为样本xi的第m种特征，其特征维数为Dm，χm表示m维的特征空间。记y={y1,y2,…,yn}，求解上述M类特征的组合问题就相当于用Ω训练分类函数f:x→y。

常用的多特征的组合方法有直接拼接法和基于核函数的特征组合方法。直接拼接法是将所有的特征并列构成一个向量，形成高维的特征向量，由于不同类型的特征具有的数值范围和特性不同，有时不容易产生整体大于局部的结果。同时，直接拼接产生的高维特征还会增加分类器训练和预测时的计算代价。

核函数的作用是把输入样本从低维空间映射到高维特征空间，因此可以表征两个样本在特征空间中的相似程度。不同的特征需要用不同的核函数去映射才能获得好的分类效果。基于核函数的特征组合方法中不同的核函数的组合方式有乘积法和线性组合法。线性组合法利用M个单核函数的线性组合来表示组合核：

(16)

其中，Km(xi,m,xj,m)表示第m种特征的核函数。对于核函数权系数dm的确定可以采取平均值法和交叉验证法，然而这些方法都有各自的局限性[16-17]，本文采用的多核学习方法能够有效地解决核函数特征组合中权系数的确定问题。与其他方法相比，该方法最大的优势是：权系数是在训练阶段自适应地通过学习获得。多核学习利用已知的训练样本，通过使目标函数最优化来学习得出每个基本核对应的权重。采用多核学习方法确定权系数不仅能避免沉重的计算代价，提高分类和识别性能，还能显示出权系数的合理性，是一种非常有效的确定权系数方法。

4 基于多特征融合多核学习SVM的液压泵故障识别

4.1 故障诊断流程

以液压泵为实验对象，研究其典型故障的诊断问题。首先对液压泵的原始振动信号用EEMD方法进行预处理，然后采用不同的特征提取方法提取AR模型系数和奇异值特征，接着对两类特征分别选择特定的核函数进行训练，使用MKL学习得到核函数的权重。这样，对液压泵的故障识别问题就转化成权系数的学习问题，进而可以得到故障识别的结果。

对液压泵原始信号EEMD分解得到的IMF分量分别用AR模型和奇异值分解提取故障特征，获取包含两种故障特征的样本。针对液压泵正常运行和不同故障状态的样本，需要选择适合特定特征的核函数，经过比较分析发现，采用径向基核函数训练AR模型特征能获得较高的分类正确率，选择多项式核函数来映射奇异值特征，能够提高故障识别的准确度。其中径向基核函数由10个不同宽度系数的基核函数组成(σ∈{0.5,1,2,5,7,10,12,15,17,20})，多项式核函数由3个不同阶数的基核函数组成(q∈{1,2,3})。

在多核学习框架下，通过采用以上两种类型的核函数分别作用两种特征，在训练阶段通过最优化联合目标函数，学习出每个核函数对应的权重。这样，对液压泵故障识别问题就转化成核函数权重学习问题，从而，可以得到故障识别结果。

基于多特征多核学习的液压泵故障识别流程如图2所示。其具体实现过程如下：

(1)从采集的液压泵各状态(正常，各种故障)的振动信号中分别截取30个样本，每个样本8192个点。

(2)对每种状态的各个样本进行EEMD分解，得到每个样本的IMF分量。

(3)将各IMF分量进行能量归一化处理，选取包含主要故障信息的前两个分量作为有效IMF分量[17]，用AR模型提取第一类特征向量。再用各IMF分量形成初始特征矩阵，提取矩阵的奇异值作为第二类特征向量。

(4)将AR模型提取的前两个IMF分量的特征向量分别用径向基核函数进行映射，将奇异值分解得到的特征向量用多项式核函数进行映射。

(5)选用训练样本，采用多特征多核学习方法训练分类器。

(6)根据训练得到的MKL支持向量机分类器来检测液压泵测试集中的样本。

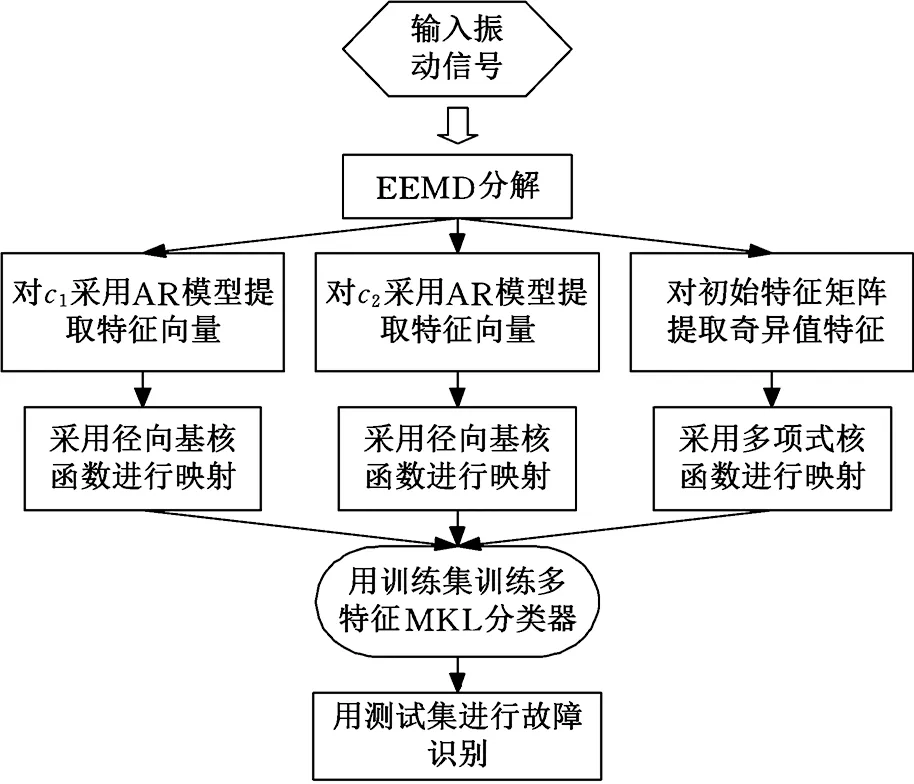
图2 多特征多核学习液压泵故障识别流程图

4.2 实验与分析

液压泵的常见故障主要有滑靴磨损、松靴、中心弹簧失效等。本实验利用振动加速度传感器对某轴向柱塞泵端盖的振动信号进行采集，分别采集液压泵正常、滑靴磨损、单柱塞松靴和中心弹簧失效四个状态的端盖振动信号。电机转速为1470 r/min，系统调定压力为15 MPa，采样频率为50 kHz。以滑靴磨损故障为例，图3所示为该故障发生时的振动加速度信号，图4给出了该信号EEMD分解后的前5个IMF分量。从图中可以看出，该方法自适应地确定了原始信号所包含的从高到低不同频率段的分量。可以针对故障信息所在的频段分量进一步提取故障特征向量。

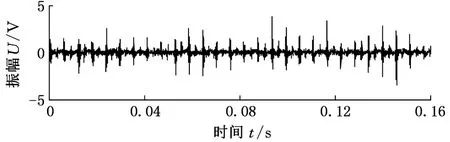
图3 滑靴磨损故障振动信号时域图

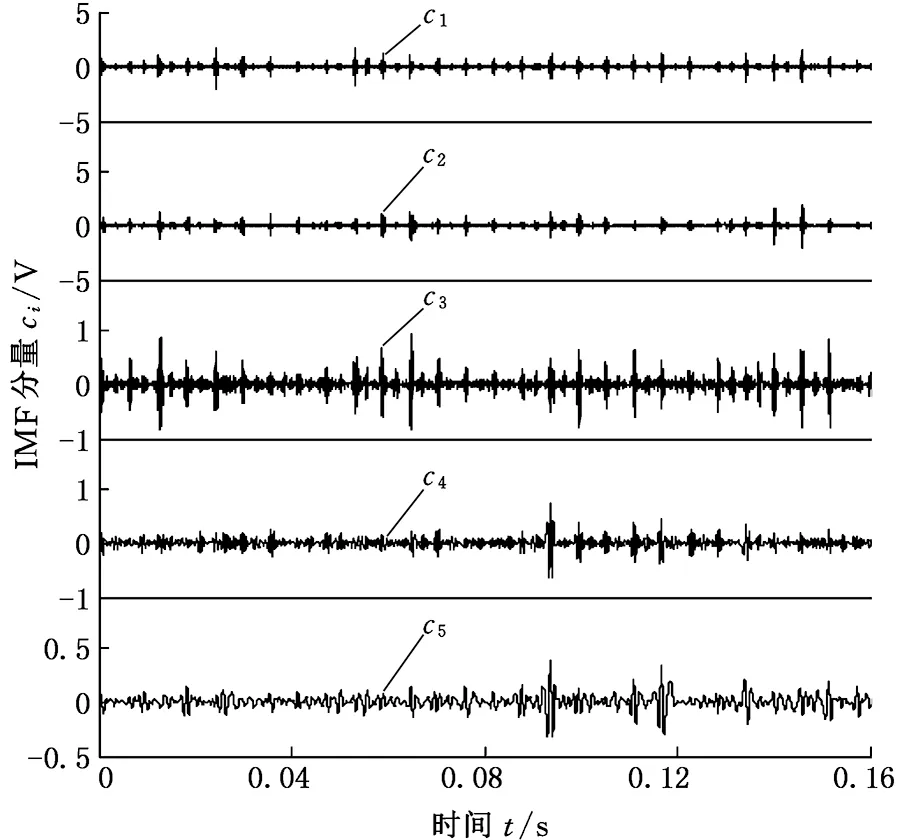
图4 滑靴磨损故障振动信号EEMD分解

对液压泵的四种状态进行分类，采用“一对多”的多分类方法[18]。在四类样本中分别随机抽取12组作为训练样本，其余的18组作为测试样本。为了验证多特征融合多核学习SVM故障识别方法在液压泵故障识别中的优越性，首先对单个特征与特征联合进行比较，即用多核学习来分别训练AR模型特征、奇异值特征，得到的故障识别结果分别与多特征联合方法进行比较；然后将不同的多特征联合方法(直接拼接法和核平均权值法)的测试结果与本文提出的多特征多核学习的检测结果进行比较分析。为进一步研究各算法在小样本时的识别情况，又将训练样本数减少一半，实验方法同上。针对单个特征以及各种特征组合方法的多核学习SVM分类结果对比如表1所示。

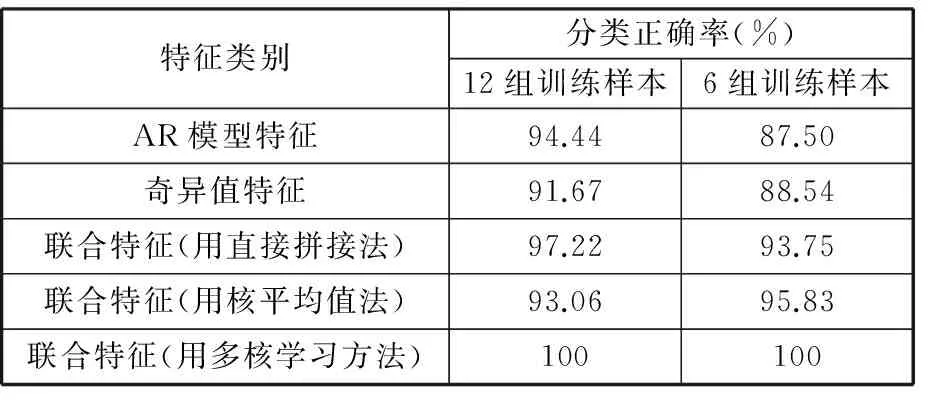
表1 多特征组合与单特征分类方法比较

从表1中可以看出，使用多特征组合方法比只使用单一特征的方法分类正确率在总体上有所提高，但是有时不容易产生整体大于局部的结果，比如训练样本为12组时用核平均值法联合特征的分类正确率低于只使用AR模型特征的分类正确率。从表中可以看出，联合特征使用多核学习方法的分类正确率最高，直接达到100%。将训练样本减少为6组，分类正确率仍为100%，可见该方法对于小样本情况也能保持很好的分类性能。多特征多核学习的故障识别方法显著地提高了液压泵故障识别的准确率。

下面对多特征多核学习SVM分类器的性能进行分析(表1最后一行)。SVM分类器的分类性能可以通过观察各类样本到最优分类超平面的距离来评价。表2给出了联合特征用多核学习方法对液压泵四种状态进行分类时，各种状态测试集中的样本到最优分类超平面距离的平均值，表中距离1是用12组样本训练的分类器所得的测试结果，距离2是用6组样本训练的分离器的测试结果。

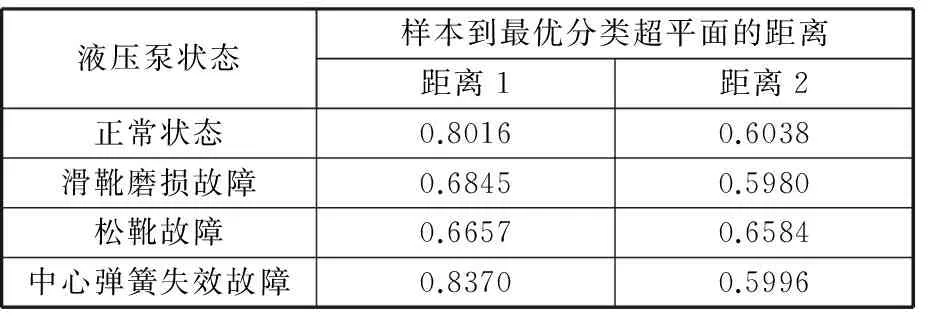
表2 各状态样本到最优分类超平面的平均距离

分析表2中对应状态的测试样本到最优超平面距离的平均值可以看到，当训练样本数减少时，多核学习SVM同样能对各状态的测试样本进行准确的分类，但是训练样本数减少后，测试样本到分类面的距离也随之减小，这表明此时分类器的总体分类性能有所降低。

图5给出了用12组样本训练后，对18组样本进行测试时，每种工作状态的各个测试样本的具体分类结果。利用单一特征分类器进行识别准确率是有限的，利用AR模型单一特征的分类结果和奇异值单一特征的分类结果分别如图5a、图5b所示，图5c是联合特征多核学习SVM的分类结果。

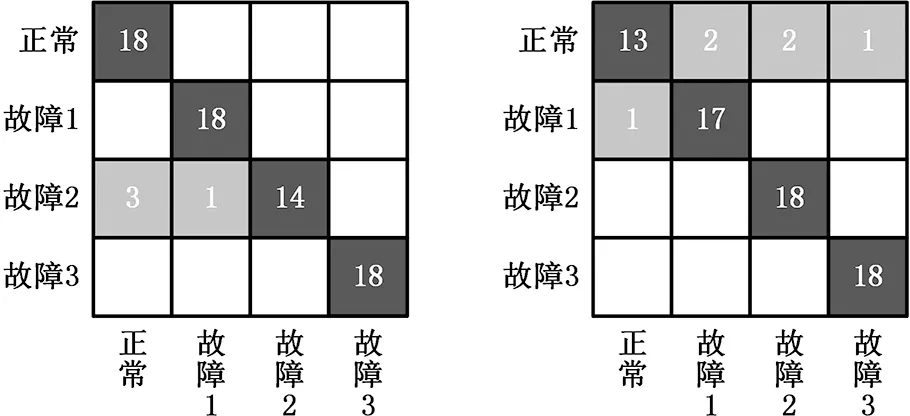
(a)AR模型单一特征 (b)奇异值单一特征

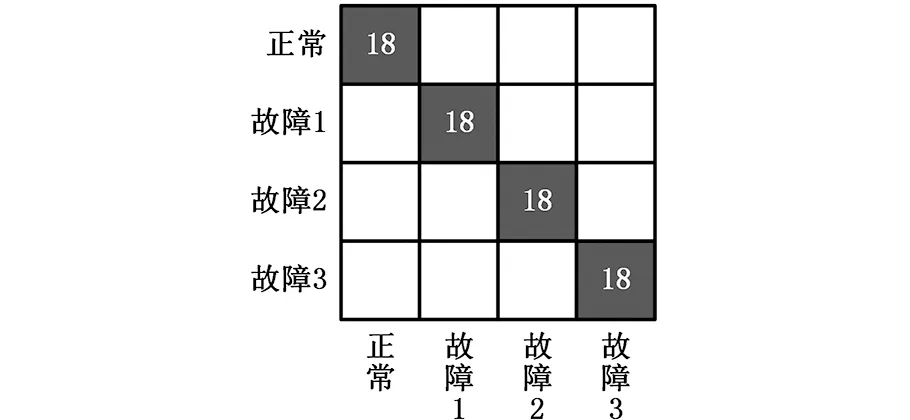
(c)多特征融合

图5中故障1、故障2、故障3分别表示滑靴磨损故障、单柱塞松靴故障、中心弹簧失效故障。图5a的第1、第2、第4行分别表示对应状态的18个测试样本均被正确分类；第3行表示故障2有14个样本被正确分类，有1个样本被误分成故障1，有3个样本被误分成正常状态。图5b第1行表示有13个样本被正确分类，有2个样本被误分成故障1，有2个样本被误分成故障2，有1个样本被误分成故障3；第2行表示有17个样本被正确分类，有1个样本被误分成正常状态；第3、第4行分别表示对应状态的18个测试样本均被正确分类。

图5a说明，对于只用AR模型特征的分类器只是将故障2误分类为其他状态；图5b说明，对于只用奇异值特征的分类器则是将正常和故障1误分类为其他状态。可见两种特征提取方法具有互补性。采用多特征多核学习方法对液压泵的故障类型进行识别弥补了仅依据单一特征分类的缺陷，实现了各种状态的准确分类，如图5c所示。因而，用多特征多核学习的旋转机械故障识别方法，将具有互补特性的特征组合起来，能够最大限度地利用可分性，显著地提高故障识别的准确性。

5 结论

(1) 与单核SVM方法相比，多核学习SVM将多个核函数进行凸组合，更有利于样本数据特征的表达，扩大了最优核函数的搜索空间，有效地提高了分类的准确率。

(2) 将EEMD与多核学习SVM结合，利用EEMD把液压泵复杂的振动信号分解成更能反映信号本质的IMF分量，有效地抑制模态混淆，为特征提取和模式识别创造了良好的前提条件，提高了故障识别的效果。

(3) 多特征多核学习的故障识别方法可以将不同的特征用不同的核函数进行映射，实现多特征的有效融合，有助于弥补各种单特征的缺点，最大限度地发挥各种特征的优势，提高分类准确率，而且在小样本情况下也具有优越的分类性能。

(4) 液压泵典型故障的诊断实验结果表明，基于多特征融合多核学习SVM的液压泵故障识别方法具有很高的故障识别准确率，具有独特的优势和良好的应用前景。

[1] 汪洪桥，孙富春，蔡艳宁，等.多核学习方法[J].自动化学报，2010，36(8)：1037-1050. Wang Hongqiao, Sun Fuchun, Cai Yanning, et al. On Multiple Kernel Learning Methods[J]. Acta Automatica Sinica, 2010, 36(8): 1037-1050.

[2] 郭创新，朱承治，张琳，等.应用多分类多核学习支持向量机的变压器故障诊断方法[J].中国电机工程学报，2010，30(13)：128-134. Guo Chuangxin, Zhu Chengzhi, Zhang Lin, et al. A Fault Diagnosis Method for Power Transformer Based on Multiclass Multiple-kernel Learning Support Vector Machine[J]. Proceedings of the CSEE, 2010, 30(13): 128-134.

[3] Lanckriet G, Cristianini N, Bartlett P, et al. Learning the Kernel Matrix with Semi-definite Programming[J]. Journal of Machine Learning Research, 2004, 5: 27-72.

[4] Lewis D P, Jebra T, Noble W S. Nonstationary Kernel Combination[C]//Proceeding of the 23rd International Conference on Machine Learning. Pittsburgh: The International Machine Learning Society, 2006: 553-560.

[5] Ong C S, Smola A J, Williamson R C. Learning the Kernel with Hyperkernels[J]. The Journal of Machine Learning Research, 2005, 6: 1043-1071.

[6] Sonnenburg S, Ratsch G, Schafer C. A General and Efficient Multiple Kernel Learning Algorithm[C]//Proceedings of the Advances in Neural Information Processing Systems. Vancouver: The MIT Press, 2005: 1273-1280.

[7] Rakotomamonjy A, Bach F, Canu S, et al. More Efficiency in Multiple Kernel Learning[C]//Proceeding of the 24th International Conference on Machine Learning. Corvallis: The International Machine Learning Society, 2007: 775-782.

[8] Bach F R, Lanckriet G, Jordan M. Multiple Kernel Learning, Conic Duality, and the SMO Algorithm[C]//Proceedings of the 21st International Conference on Machine Learning. Alberta: The International Machine Learning Society, 2004: 41-48.

[9] Sonnenburg S, Ratsch G, Schafer C, et al. Large Scale Multiple Kernel Learning[J]. The Journal of Machine Learning Research, 2006, 7: 1531-1565.

[10] 何正嘉，訾艳阳，张西宁.现代信号处理及工程应用[M].西安：西安交通大学出版社，2007.

[11] Huang N E, Shen Z, Long S R, et a1. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Nonstationary Time Series Analysis[J]. Proceedings of the Royal Society, 1998, 454(1971): 903-995.

[12] Wu Z H, Huang N E. Ensemble Empirical Mode Decomposition: a Noise Assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.

[13] 于德介，杨宇，程军圣.一种基于SVM和EMD的齿轮故障诊断方法[J].机械工程学报，2005，41(1)：140-144. Yu Dejie, Yang Yu, Cheng Junsheng. Fault Diagnosis Approach for Gears Based on EMD and SVM[J]. Chinese Journal of Mechanical Engineering, 2005, 41(1): 140-144.

[14] 程军圣，于德介，杨宇.基于内禀模态奇异值分解和支持向量机的故障诊断方法[J].自动化学报，2006，32(3)：475-480. Cheng Junsheng, Yu Dejie, Yang Yu. Fault Diagnosis Approach Based on Intrinsic Mode Singular Value Decomposition and Support Vector Machines[J]. Acta Automatica Sinica, 2006, 32(3): 475-480.

[15] Rakotomamonjy A, Bach F R, Canu S, et al. Simple MKL[J]. The Journal of Machine Learning Research, 2008, 9: 2491-2521.

[16] Vedaldi A, Gulshan V, Varma M, et al. Multiple Kernels for Object Detection[C]//Proceedings of IEEE 12th International Conference on Computer Vision. Kyoto: Institute of Electrical and Electronics Engineers， 2009： 606-613.

[17] 刘志强.基于多核学习支持向量机的旋转机械故障识别方法研究[D].秦皇岛：燕山大学，2014.

[18] Lee Y, Lin Y, Wahba G. Multicategory Support Vector Machines: Theory and Application to the Classification of Microarray Data and Satellite Radiance Data[J]. Journal of the American Statistical Association, 2004, 99(465): 67-81.

(编辑 王艳丽)

Fault Identification Method for Hydraulic Pumps Based on Multi-feature Fusion and Multiple Kernel Learning SVM

Liu Zhiqiang1,2，3Jiang Wanlu1,2Tan Wenzhen3Zhu Yong1,2

1.Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control,Yanshan University,Qinhuangdao，Hebei,0660042.Key Laboratory of Advanced Forging & Stamping Technology and Science,Ministry of Education of China,Qinhuangdao，Hebei,0660043.Tangsteel High Strength Automotive Strip Co.,Ltd.,Tangshan，Hebei,063002

A hydraulic pump fault identification method was put forward based on multiple feature fusion and multiple kernel learning SVM. Firstly, the original signals were processed by the ensemble empirical mode decomposition. Then, the feature vectors of hydraulic pump faults were obtained by using the autoregressive model and the singular value decomposition. Through different types of features mapped by corresponding different kernel functions, the hydraulic pump working conditions and fault types might be finally identified by multiple kernel learning SVM. The experimental results show that the approach improves the accuracy of fault diagnosis significantly.

multiple kernel learning; multi-feature fusion; support vector machine(SVM); fault identification; hydraulic pump

2015-11-30

国家自然科学基金资助项目(51475405)；国家重点基础研究发展计划(973计划)资助项目(2014CB046405)；河北省自然科学基金资助项目(E2013203161)

TP277

10.3969/j.issn.1004-132X.2016.24.016

刘志强，男，1987年生。燕山大学机械工程学院硕士，唐钢高强汽车板有限公司助理工程师。主要研究方向为故障诊断与智能信息处理。姜万录(通信作者)，男，1964年生。燕山大学机械工程学院教授、博士研究生导师。谭文振，男，1964年生。唐钢高强汽车板有限公司冷轧部高级工程师、博士。朱 勇，男，1986年生。燕山大学机械工程学院博士研究生。