多因素影响的电子螺旋导轨误差的理论分析

吴震宇 赵大兴 钟瑞龄

1.湖北工业大学，武汉，430068 2.宜昌长机科技有限责任公司，宜昌，443003

多因素影响的电子螺旋导轨误差的理论分析

吴震宇1赵大兴1钟瑞龄2

1.湖北工业大学，武汉，430068 2.宜昌长机科技有限责任公司，宜昌，443003

为了进一步提高电子螺旋导轨对内斜齿的加工精度，从插齿机传动链机构运动学的角度，研究了内斜齿螺旋线偏差的产生机理。首先，根据插削时各轴的运动关系，建立了插齿刀附加转动的数学模型，定义了附加转动系数；然后，分别建立了附加转动偏差以及主运动曲线偏差与螺旋线偏差之间的数学关系，定义了Zebra系数；最后，分析了螺旋线偏差的产生机理，总结了杆件长度、曲柄初始位置以及运动副间隙对螺旋线偏差的影响规律。

插齿机；电子螺旋导轨；附加转动；曲柄滑块机构

0 引言

普通国产插齿机通常采用机械式螺旋导轨插削斜齿轮，当加工不同螺旋角的斜齿轮时就必须要更换螺旋导轨[1]。由于螺旋导轨的制造工艺复杂、加工成本高而且不易更换，导致内斜齿轮加工效率和加工精度难以满足要求，因此，采用电子螺旋导轨取代机械式螺旋导轨，这一方面节约了加工螺旋导轨所产生的制造成本[2]，另一方面，缩短了安装螺旋导轨所需的工时，提高了生产效率[3]，此外，还规避了机械螺旋导轨制造和安装误差对齿轮加工精度的影响[4-5]。目前宜昌长机科技有限责任公司生产的YK5150型带电子螺旋导轨的数控插齿机能够保证插齿精度达到6级。由斜齿圆柱齿轮齿面成形方法可知[6]，展成运动和附加转动同步进行才能完成斜齿轮的插削加工，实现附加转动是斜齿轮插削加工的关键。以往，插齿刀附加转动的实现是靠机械式螺旋导轨实现的，如果采用电子螺旋导轨代替机械螺旋导轨，首先要解决的问题是附加转动的实现。关于这个问题，目前已经从理论上证明附加运动是可以通过插齿刀来完成的，并且已有学者建立了附加转动的数学模型[7-8]，但实际加工的内斜齿轮螺旋线精度仍然与设计值存在偏差，这不是由于理论模型不正确所导致的，而是对螺旋线偏差的产生机理研究不足，从而导致实际应用中不能有效规避产生误差的主要因素。电子螺旋导轨附加转动不是靠机械装置实现的，该转动与插齿刀轴向直线位移存在运动关系，螺旋线偏差是受到多因素影响而产生的。本文依据数控插齿机传动链机构学原理，以数控螺旋导轨附加转动的数学模型为分析基础，从定性和定量的角度研究螺旋线偏差的产生机理。

1 插削斜齿轮所需的运动关系

1.1 插削斜齿轮时各轴的运动关系

图1为数控斜齿轮插齿机传动原理图，图中点划线部分表示由数控系统实现的相关轴的运动关系[9]。

图1 数控斜齿轮插齿机传动原理图

图1中，E轴为主轴，带动刀具上下往复运动，正常工作时应匀速旋转；C轴带动工作台旋转，正常工作时匀速旋转或者间歇性旋转，完成圆周进给；X轴间歇性旋转，完成径向进给；B轴带动刀具旋转，其运动关系最复杂，由展成运动及附加转动组成，对工件的螺旋线精度有直接影响。如图1所示，B轴因附加展成运动转过的角度与C轴转过的角度成齿数比，还与E轴转过的角度之间呈一较复杂的函数关系。因此实现斜齿轮插削加工数控化的关键在于对B轴的控制。

1.2 插削斜齿轮所需的附加转动关系

插削斜齿轮时，插齿刀除了做展成运动，还要相对工件做附加转动。当附加转动由插齿刀来完成时，其要求为：插齿刀分度圆上一点转过的距离除以插齿刀竖直方向上的移动距离L等于分度圆螺旋角β的正切值，即

(1)

式中，mn为插齿刀模数；zD为插齿刀齿数。

由此可以推出附加转动角度公式：

(2)

当附加转动由工件来完成时，只需将式(2)中的zD用工件的齿数代替即可。

由式(2)可知，当插齿刀的模数、齿数、螺旋角已知时，插齿刀附加转动角度θ与插齿刀在竖直方向上运动的距离L成固定比例，称该比例为附加转动系数，用K表示，即

(3)

2 螺旋线偏差计算模型

2.1 附加转动偏差与螺旋线偏差

图2 螺旋线偏差计算示意图

即工件齿轮螺旋线偏差等于基圆半径与工件齿轮转动偏差角的乘积。由于工件齿轮转动偏差是由插齿刀附加转动偏差引起的，所以工件齿轮螺旋线偏差与插齿刀附加转动偏差角之间的关系可用下式表示：

(4)

式中，θD为插齿刀附加转动偏差角。

2.2 主运动曲线偏差与螺旋线偏差

插齿刀在竖直方向上的主运动通常由曲柄滑块机构实现。以曲柄转角为自变量，以插齿刀在竖直方向上的移动距离为因变量，得到的曲线称为主运动曲线。

计算插齿刀附加转动值时，需要假设插齿刀在竖直方向上的移动距离与曲柄转角之间的关系，称它们之间的关系曲线为插齿刀的理论主运动曲线。与之相对应的是插齿刀实际移动距离与曲柄转角之间的关系，称它们之间的关系曲线为插齿刀的实际主运动曲线。将插齿刀实际附加转动角度除以附加转动系数，以得到的商为纵坐标，以曲柄转角为横坐标，得到的曲线称为设计主运动曲线。定义任一曲柄转角对应的设计主运动曲线偏差为：以该曲柄转角为主运动曲线上点的横坐标值，对应的设计主运动曲线上点的纵坐标值与实际主运动曲线上点的纵坐标值的差值。定义任一曲柄转角对应的理论主运动曲线偏差为：以该曲柄转角为主运动曲线上点的横坐标值，对应的理论主运动曲线上点的纵坐标值与实际主运动曲线上点的纵坐标值的差值。除非另有声明，下文中的主运动曲线偏差均指设计主运动曲线偏差。

通过式(2)可以由主运动曲线偏差得到插齿刀的附加转动偏差，通过式(4)可以由插齿刀的附加转动偏差得到工件齿轮的螺旋线偏差。所以主运动曲线偏差ΔL与螺旋线偏差e之间的关系可由下式表示：

(5)

又

tanαt=tanαn/cosβ

得到

代入式(5)得

(6)

由式(6)可知，螺旋线偏差是由主运动曲线偏差所引起的。

法面压力角αn恒等于20°，由式(6)可知，确定螺旋角β的值之后，主运动曲线的偏差将以固定的比例反映到工件齿轮的螺旋线偏差上，称该比例系数为Zebra系数，用Z表示，即

(7)

插削斜齿轮时，在螺旋线计值范围内任意位置处，主运动曲线偏差乘以斜齿轮螺旋角所对应的Zebra系数，即可得到该位置的螺旋线偏差。

3 螺旋线偏差的等效分析

由前面的分析可知，螺旋线偏差与主运动曲线偏差之间相差了一个Zebra系数，因此，对螺旋线偏差的分析可以转化成对主运动曲线偏差的分析。如果主运动曲线偏差为零，那么螺旋线偏差也就为零。因此本节将围绕“如何实现主运动曲线偏差为零，主运动曲线偏差与哪些影响因素有关”等问题展开研究。

由2.2节主运动曲线偏差的定义可知，要想实现主运动偏差为零，理想情况是设计主运动曲线、理论主运动曲线以及实际主运动曲线三条曲线重合。

3.1 设计主运动曲线与理论主运动曲线的重合性分析

首先对主运动曲线与理论主运动曲线能否重合进行分析。当采用曲柄滑块机构实现主运动时，假设曲柄从最高点开始旋转，按逆时针方向旋转，则可采用下式表示的曲线作为理论主运动曲线[10]：

(8)

式中，L1为连杆长度；L2为曲柄长度；θ为曲柄旋转角度；Lθ为插齿刀在竖直方向上的移动距离。

当连杆长度为170 mm，曲柄长度为120 mm时，按式(8)计算得到的理论主运动曲线如图3所示，当采用曲柄连杆机构实现插齿刀的主运动时，理论主运动曲线呈非线性。因此，实际应用中很难保证设计主运动曲线与理论主运动曲线重合。设计主运动曲线事实上是由一系列的直线段构成的。这一系列的直线段按照一定的规律逼近理论主运动曲线，不可避免地存在逼近偏差。但是，为了解决逼近偏差引起的问题，可以按照一定的规则，限制设计主运动曲线的逼近偏差，进而使任意位置的螺旋线偏差小于许用螺旋线偏差。

图3 理论主运动曲线图

由上述分析可知，尽管设计主运动曲线与理论主运动曲线不能完全重合，但还是可以通过逼近原则实现两条曲线的无限接近。

3.2 实际主运动曲线与理论主运动曲线的重合性分析

由3.1节分析可知，设计主运动曲线是可以无限逼近理论主运动曲线的，如果实际主运动曲线能够与理论主运动曲线重合或者无限逼近，那么螺旋线误差就能够接近于零。但是受杆件长度及曲柄初始位置测量精度、运动副间隙、杆件受力变形以及磨损等因素的影响，实际主运动曲线与理论主运动曲线往往并不重合。因此，由逼近理论主运动曲线得到的设计主运动曲线，不可避免地与实际主运动曲线存在偏差，即设计主运动曲线偏差不等于0。以下着重分析杆件长度及曲柄初始位置测量精度、连杆机构运动副间隙引起的主运动曲线偏差，以及因此引起的螺旋线偏差、螺旋线总偏差。为了分析简便起见，在本节的分析中忽略设计主运动曲线的逼近偏差，即假设设计主运动曲线与理论主运动曲线重合。

3.2.1 杆件长度及曲柄初始位置测量精度对主运动曲线偏差的影响

不考虑其他因素的影响，假设理论连杆长度为L1，理论曲柄长度为L2，理论初始角度为0，实际连杆长度为L1+ΔL1，实际曲柄长度为L2+ΔL2，实际初始角度为Δθ。结合式(8)可得实际主运动曲线与理论主运动曲线的差值，即主运动曲线偏差为

Δ(L1,L2,θ,ΔL1,ΔL2,Δθ)=

Lθ(L1+ΔL1,L2+ΔL2,θ+Δθ)-Lθ(L1,L2,θ)

(9)

当螺旋角β取15°时，按照式(7)计算Zebra系数等于0.251，即可得到螺旋线偏差。

图4为L1为170 mm，L2为120 mm，ΔL2为0，Δθ为0，ΔL1分别为-0.5 mm、0.5 mm、1 mm时对应的主运动曲线偏差，当实际连杆长度比理论连杆长度大0.5 mm时，最大主运动曲线偏差出现在曲柄转角为90°处，其大小为0.205 mm。取螺旋角β为15°，则最大螺旋线偏差为0.0515 mm。按国家标准，它能够满足的最高精度的齿轮是精度等级为7级、分度圆直径范围为(1600，2500]mm、齿宽范围为(650，1000]mm的齿轮。

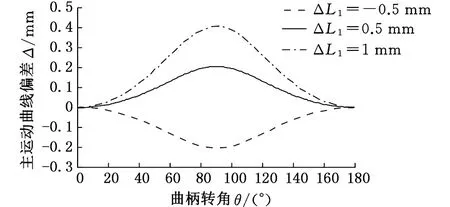
图4 实际连杆长度对主运动曲线偏差的影响

图5为L1为170 mm，L2为120 mm，ΔL1为0，Δθ为0，ΔL2分别为-0.5 mm、0.5 mm、1 mm时对应的主运动曲线偏差曲线，假设上超越行程及下超越行程均为20 mm，加工行程为200 mm，当实际曲柄长度比理论曲柄长度大0.5 mm时，最大主运动曲线偏差出现在154°，其大小为0.878 mm。取螺旋角β为15°，则最大正螺旋线偏差为0.2204 mm。按国家标准，它能够满足的最高精度的齿轮规格为11级精度的分度圆直径范围为(2500，4000]mm、齿宽范围为(650，1000]mm的齿轮。

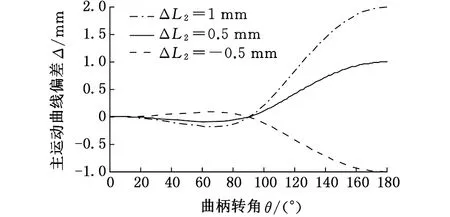
图5 实际曲柄长度对主运动曲线偏差的影响

图6为L1为170 mm，L2为120 mm，ΔL1为0，ΔL2为0，Δθ分别为-0.5°、0.5°、1°时对应的主运动曲线偏差。当实际初始位置为0.5°时，最大主运动曲线偏差出现在116°，偏差大小为1.318 mm。取螺旋角β为15°，则最大螺旋线偏差为0.3308 mm。按国家标准，只能加工分度圆直径范围为(6000，10000]mm、齿宽范围为(650，1000]mm、精度等级为12级的齿轮。

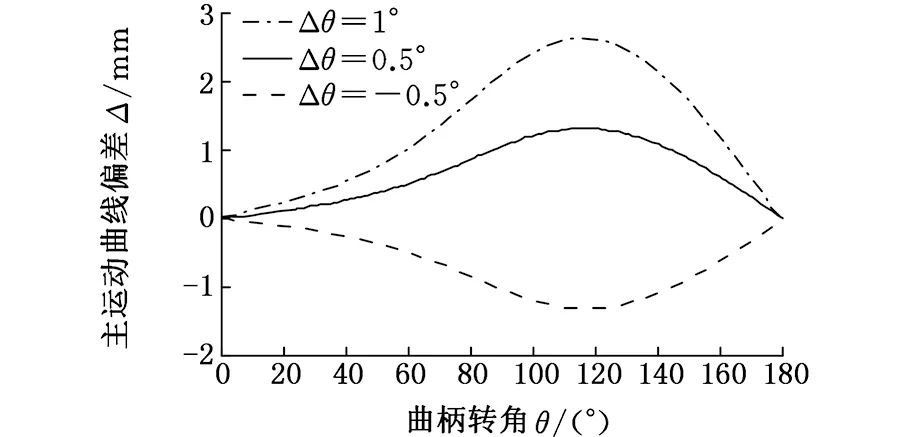
图6 实际初始位置对主运动曲线偏差的影响

可见，实际连杆长度、实际曲柄长度、实际初始位置分别单独作用时，对主运动曲线偏差和最大螺旋线偏差的影响的大小及规律各不相同。现实中三者往往共同作用，实际主运动曲线与理论主运动曲线的偏离更严重，并且没有简单可靠的规律可以遵循。

3.2.2 运动副间隙对主运动曲线偏差的影响

为了分析简便起见，忽略其他因素的影响，不考虑曲柄与底座相接的转动副的间隙以及滑块与底座相接的移动副的间隙。只考虑曲柄与连杆相接的转动副间隙以及连杆与滑块相接的转动副间隙对实际主运动曲线的影响。根据插削齿轮过程中滑块受力及连杆传递力的情况，将运动副间隙对主运动曲线的影响分为三种情况：上下超越行程中运动副间隙的影响；切削行程中运动副间隙的影响；超越行程与切削行程过渡阶段运动副间隙的影响。假设实际连杆长度为l1，实际曲柄长度为l2，曲柄从最高点开始旋转，按逆时针方向旋转。假设所有转动副的销和孔的作用面都是理想的圆柱面，曲柄与连杆相接的转动副的销与孔半径的差为Δ1，连杆与滑块相接的转动副的销与孔半径的差为Δ2。转动副通过销与孔的接触传递运动和力。同时其作用面假定为理想的圆柱面。因此，只要传递的运动和力不为0，转动副中销的中心线必然在以相对应的孔的中心线为中心、以两者作用面半径之差为半径的圆柱面上。并且，传递不同的运动和力时，销的中心线在圆柱面上的位置不同。

3.2.2.1 超越行程中运动副间隙的影响

在上下超越行程中，除去超越行程与切削行程过渡阶段，连杆主要受滑块重力的作用。在重力的作用下，运动副的销与孔的间隙使滑块的实际行程大于理论行程，并且在某一特定位置能够使两者之差达到最大值。

图7所示为超越行程中运动副间隙对主运动曲线的影响。在超越行程中的任一位置，由于重力的作用，转动副1的销与孔的中心连线在连杆的延长线上，同时转动副2的销与孔的中心连线也在连杆的延长线上。可以证明，此时滑块的实际行程已经超出了理论行程，并且两者之差达到最大值。

图8为超越行程曲柄与连杆相接的转动副中销位置的计算示意图。销的中心在以孔的中心为中心，以Δ1为半径的圆上。同时，销的中心必须在以连杆另一端为中心，以连杆长度l1为半径的圆上。连杆的另一端在对心线上移动。所以，销的中心在两个圆的交点上。显然，当两圆相外切时，连杆的另一端离曲柄的旋转中心最远。此时，销与孔的中心连线在连杆的延长线上。同理，对于连杆与滑块相接的转动副，当销与孔的中心连线在连杆的延长线上时，滑块上的转动副中心离曲柄的旋转中心最远。

图7 超越行程中运动副间隙对主运动曲线的影响

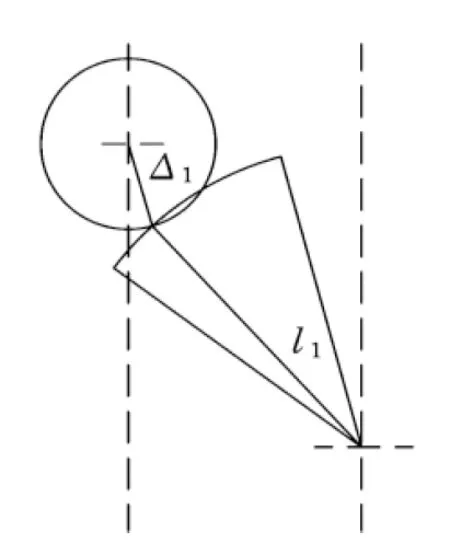
图8 超越行程转动副中销位置计算示意

由以上分析可知，在超越行程中，连杆的作用长度等于连杆的实际长度与两转动副孔与销的半径之差的和，即l1+Δl1=l1+Δ1+Δ2。由此引起的主运动曲线偏差为

Δ(l1,l2,θ,Δl1,Δl2,Δθ)=lθ(l1+Δ1+Δ2,l2,θ)-lθ(l1,l2,θ)

(10)

由式(10)可知，在假定条件下，超越行程中两转动副间隙对主运动曲线的影响等价于实际连杆长度大于理论连杆长度所造成的影响。

3.2.2.2 切削行程中运动副间隙的影响

在切削行程中，连杆需要将力传递到滑块上以克服切削阻力。此时，运动副中销与孔的间隙会导致滑块的实际行程小于理论行程，同时存在某一特定位置能够使两者之差达到最大值。

图9所示为切削行程中运动副间隙对测量精度的影响。在切削力的作用下，转动副1的销与孔的中心连线在连杆上，转动副2的销与孔的中心连线也在连杆上。可以证明，此时滑块的实际行程小于理论行程，并且两者之差达到最大值。

图10为切削行程曲柄与连杆相接的转动副中销位置的计算示意图。销的中心在以孔的中心为中心，以Δ1为半径的圆上。同时，销的中心必须在以连杆另一端为中心，以连杆长度l1为半径的圆上。连杆的另一端在对心线上移动。所以，销的中心在两个圆的交点上。显然，当两圆相内切时，连杆的另一端离曲柄的旋转中心最近。此时，销与孔的中心连线在连杆上。同理，对于连杆与滑块相接的转动副，只有当销与孔的中心连线在连杆上时，滑块上的转动副中心离曲柄的旋转中心最近。

图9 切削行程中运动副间隙对主运动曲线的影响

图10 切削行程转动副中销位置计算示意

由以上分析可知，在切削行程中，连杆的作用长度等于连杆的实际长度减去两转动副孔与销的半径之差，即l1+Δl1=l1-Δ1-Δ2。由此引起的主运动曲线偏差为

Δ(l1,l2,θ,Δl1,Δl2,Δθ)=lθ(l1-Δ1-Δ2,l2,θ)-lθ(l1,l2,θ)

(11)

由式(11)可知，在假定的条件下，切削行程中两转动副间隙对主运动曲线的影响等价于实际连杆长度小于理论连杆长度造成的影响。

3.2.2.3 过渡阶段运动副间隙的影响

如前所述：在上超越行程与切削行程的过渡阶段之前，运动副间隙对主运动曲线的影响等价于实际连杆长度增大带来的影响；在切削行程中，运动副间隙对主运动曲线的影响等价于实际连杆长度减小带来的影响；在切削行程与上超越行程的过渡阶段之后，运动副间隙对主运动曲线的影响等价于实际连杆长度增大带来的影响。

当插齿刀最下端与被加工齿轮上表面接触时，上超越行程与切削行程的过渡阶段开始。在该过渡阶段，滑块的实际位置没有改变，滑块的理论位置逐渐增大。当滑块的理论行程大于实际行程并且两者之间的距离达到最大值时，该过渡阶段结束，进入切削行程。

在切削行程末端，当切削阻力等于重力作用时，切削行程与下超越行程的过渡阶段开始。滑块的理论行程随着曲柄转角的增大而增大，但是由于重力作用大于切削阻力的作用，因此，滑块实际行程的增长速度要大于理论行程的增长速度。当滑块的实际行程大于理论行程并且两者之差达到最大值时，该过渡阶段结束，进入切削下超越行程的剩余部分。

在两个过渡阶段，运动副间隙的影响等价于实际初始角度不等于理论初始角度以及实际连杆长度不等于理论连杆长度这两种因素共同作用造成的影响。在第二个过渡阶段，还受到实际切削阻力大小的影响。这两个过渡阶段很难找到简单可靠的规律来描述其影响，这里只给出定性的描述。

根据国家标准：迹线长度与齿宽成正比但不包括齿端倒角或修缘在内的长度；螺旋线计值范围是指在轮齿两端处各减去5%的齿宽或一个模数的长度两者中较小的一个后的迹线长度。因此，可以认为这两个过渡阶段在螺旋线计值范围之外。在螺旋线计值范围之内，运动副间隙对主运动曲线的影响等价于实际连杆长度减小带来的影响。

结合之前的分析：若实际连杆长度大于理论连杆长度，运动副间隙将使螺旋线计值范围之内的主运动曲线偏差减小；若实际连杆长度小于理论连杆长度，运动副间隙将使螺旋线计值范围之内的主运动曲线偏差的绝对值增大。确定理论连杆长度时，应该取多次测量得到连杆长度测量值的最小值，或者取连杆长度测量值的最大值与运动副间隙测量值的最大值的差。

4 结论

(1)通过对插削斜齿轮时各轴的运动关系分析，明确了加工斜内齿轮所需的附加转动是可以通过插齿刀来完成的，并且建立了电子螺旋导轨附加转动数学模型，该模型表明刀具的附加转动与刀轴的主运动之间是存在耦合关系的。

(2)依据螺旋线偏差的定义，建立了附加转动偏差与螺旋线偏差的数学关系式；根据刀具附加转动与刀轴主运动位移之间的运动关系，建立了主运动偏差与螺旋线偏差之间的数学关系式，由该式可知，螺旋线偏差是由主运动偏差引起的。

(3)根据主运动偏差与螺旋线偏差之间的数学关系式，将螺旋线偏差分析等效成主运动曲线偏差分析。由分析可知，设计主运动曲线只能逼近理论主运动曲线，因此螺旋线偏差不可避免；另外，杆件长度、曲柄初始位置以及运动副间隙对螺旋线偏差都有影响。

[1] 程伟林.具有急回特性的数控插齿机主运动系统的设计与控制研究[D].株洲：湖南工业大学，2015.

[2] Kapil G, Laubscher R F, Paulo D J, et al.Recent Developments in Sustainable Manufacturing of Gears: a Review[J]. Journal of Cleaner Production,2016,112(4):3320-3330.

[3] Chen S H, Zhang Hua, Fong Z H.Study on the Cutting Time of the Hypoid Gear Tooth Flank[J]. Mechanism and Machine Theory, 2015,84:113-124.

[4] Colbourne J R. Geometric Design of Internal Gear Pairs[J]. Gear Technology, 2014, 7(3): 28-37.

[5] Kawasaki K, Tsuji I, Gunbara H. Manufacturing Method of Double-helical Gears Using CNC Machining Center[J].Journal of Mechanical Engineering Science,2015,230(7):1149-1156.

[6] 江甫炎.近代齿轮制造工艺[M].北京：航空工业出版社, 1994.

[7] Liu Youyu. Research on Gear Shaping Strategy for Internal Helical Non-circular Gears and Performance Analyses for Linkage Models[J]. Journal of Mechanical Science and Technology,2014,28(7): 2749-2757.

[8] 胡赤兵,刘洪芹,李楠,等.斜齿轮插削加工CNC 系统[J].兰州理工大学学报,2004,30(1):42-44. Hu Chibing, Liu Hongqin, Li Nan, et al. CNC System of Helical Gear Shaping[J]. Journal of Lanzhou University of Technology, 2004,30(1):42-44.

[9] 朱玉.斜齿轮数控插削加工的运动分析和仿真[J].机械传动,2008,32(5):69-72. Zhu Yu. Kinematics Analysis and Simulation of NC Shaping of Helical Gear[J]. Journal of Mechanical Transmission,2008,32(5):69-72.

[10] 魏兵，杨文堤.机械设计基础[M].武汉：华中科技大学出版社，2011.

(编辑 王艳丽)

Theoretical Analyses on Errors of Electronic Helical Guides Influenced by Multi-factors

Wu Zhenyu1Zhao Daxing1Zhong Ruiling2

1.Hubei University of Technology,Wuhan,4300682.Yichang Changji Machine Technology Co.,Ltd.,Yichang，Hubei,443003

For improving the internal helical gear machining precision of electronic helical guides, this paper analysed the principles about how to cause the errors of spiral line of internal helical gears according to kinematics of the driving chains in a gear shaping machine. Firstly, a mathematical model of additional rotation of the tool was established according to the kinematic relationship of several axles, and an additional rotation coefficient was defined. Then, the mathematical relationships among the errors of spiral line and the errors of additional rotation and main motion were established respectively, and a coefficient Zebra was defined. At last, the mechanism causing the errors of spiral line was analyzed, and the influences of the length of rods and the position of crank and the gap of motion joints on the error of spiral line were concluded.

gear shaping machine; electronic helical guide; additional rotation; slider crank mechanism

2016-05-26

国家自然科学基金资助项目(51075130)；湖北省重大科技专项(2014AAA013，2016AAA068)；高层次人才科研启动金资助项目(BSQD385)

TH161

10.3969/j.issn.1004-132X.2016.24.007

吴震宇，男，1982年生。湖北工业大学机械工程学院副教授。主要研究方向为智能控制与数控技术。赵大兴，男，1962年生。湖北工业大学机械工程学院教授、博士研究生导师。钟瑞龄，男，1968年生。宜昌长机科技有限责任公司高级工程师。