任意阶PDE降噪特性分析*
尹爱军, 张 泉,2, 戴宗贤
(1.重庆大学机械传动国家重点实验室 重庆,400044) (2.天津送变电工程公司 天津,300161)(3.重庆市计量质量检测研究院第一分院 重庆,402260)
任意阶PDE降噪特性分析*
尹爱军1, 张 泉1,2, 戴宗贤3
(1.重庆大学机械传动国家重点实验室 重庆,400044) (2.天津送变电工程公司 天津,300161)(3.重庆市计量质量检测研究院第一分院 重庆,402260)
通过对分数阶微积分原理的研究,提出了任意阶偏微分方程(partial differential equations, 简称PDE)降噪的统一模型,实现了基于任意阶PDE降噪的数值化方法,并分析了任意阶PDE降噪特性。该数值化方法能够快速实现信号降噪,耗时少。通过仿真实验,分析了PDE降噪性能的影响因素,与其他去噪方法进行了对比分析,并对现场实测信号进行了降噪分析。结果表明,PDE数值求解降噪方法性能优良,算法简单。
偏微分方程; 分数阶; 降噪; 振动信号
引 言
信号降噪在信号特征提取和参数化中具有重要的意义。滤波降噪理论与方法获得了广泛深入的研究,其理论从一般的平稳信号降噪方法发展到各种非平稳信号降噪方法,如小波去噪、经验模态分解(empirical mode decomposition, 简称EMD)、奇异值分解降噪及滑动平均滤波等降噪方法[1]。小波变换是一种很好的非平稳信号降噪方法,得到了广泛的研究和应用[2]。不同的小波基及阈值对去噪效果有很大影响[3]。EMD具有良好的自适应时频分析能力,但EMD需要先验知识,降低了该算法的鲁棒性[4-5]。奇异值分解降噪是一种非线性滤波方法,奇异值数目选取是其降噪效果好坏的关键,但有效阶次的选择并没有明确方法[6]。滑动平均滤波能够有效抑制随机误差,提高信噪比,但高频变化的确定性成分会因平均而被削弱[7]。偏微分方程(PDE)在图像去噪、图像增强等方面取得了很好的应用效果[8-9]。PDE在一维振动信号也得到一些应用,Baravdish等[10]通过矩阵奇异值分解与PDE实现对音频信号进行降噪。Yin等[11]研究了基于PDE的信号修补方法,在EMD端点效应处理取得了很好的效果。文献[12]将PDE用于振动信号去噪取得了很好的实际应用效果。和整数阶PDE一样,分数阶PDE受到广泛的关注。Pu等[13]通过分数阶的PDE降噪模型对二维图像信号进行降噪,取得了更好的效果。Bai等[14]利用非线性的各向异性分数阶扩散方程获得更自然的影像。然而,分数阶 PDE的阶次被限制在一个很小的范围内,这影响了PDE降噪效果。
笔者根据分数阶微积分原理,从传统滤波器的幅频特性角度出发,提出了任意阶PDE降噪的统一模型,并研究了PDE滤波器的设计方法以及基于PDE降噪的数值化方法,建立了基于数值解降噪的一般过程。通过仿真实验,分析了PDE降噪性能的影响因素,并与小波去噪等方法进行了对比分析。结果表明,PDE数值求解降噪方法性能优良,算法简单。
1 任意阶PDE滤波模型
1.1 分数阶微积分定义
从不同的应用角度去分析问题可以得到不同的分数阶微积分定义。至今为止,分数阶微积分仍没有统一的定义表达式[15]。目前,主要有4种经典的分数阶微积分定义:Grünwald-Letnikov,Capotu,Riemann-Liouville和Cauchy定义。其中,后3种定义使用了Cauchy积分公式,计算复杂度较高,不利于分数阶微分数值计算。
Grünwald-Letnikov定义是对整数阶微分的差分近似递推而来。式(1)为Grünwald-Letnikov分数阶微积分定义表达式
(1)
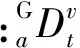

Riemann-Liouville分数阶的微积分定义是对Grünwald-Letnikov定义的改进,有
(2)
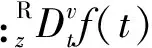
在一定条件下,可由Grünwald-Letnikov型分数阶导数定义获得Riemann-Liouville型分数阶导数的数值化解法[16]。
Riemann-Liouville型分数阶导数具有如下复合运算法则
(3)
1.2 任意阶PDE滤波原理
笔者根据热传导方程,从滤波器角度推导了整数阶偏微分方程的滤波原理和方法[11-12]。在这些研究基础上,分析任意阶偏微分方程的滤波特性。定义分数阶偏微分方程式为
(4)
当f(x,t)=0时,利用傅里叶变换法,式(4)为
(5)
解得
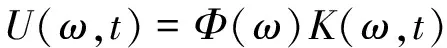
(6)
其中:U(ω,t)=F(u(x,t)),Φ(ω)=F(φ(x))分别为u(x,t),φ(x)的关于x的傅里叶变换。
K(ω,t)为
(7)
当φ(x)表示原始信号时,式(4)的解即为对信号φ(x)的滤波过程,K(ω,t)即为滤波器频率响应。
因在复数域中,(iω)v可表示为
则式(7)可以表示为
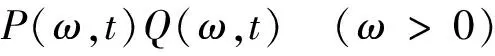
(8)
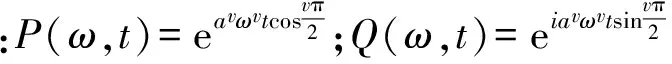
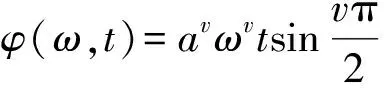
若偏微分方程的阶次v为奇数,幅频特性为
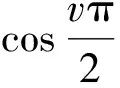
(9a)
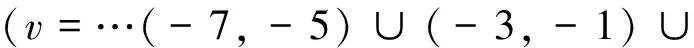

(9b)
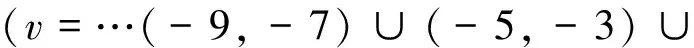
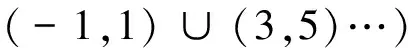
进一步可得到任意阶PDE降噪模型
(10)

定义信号φ(x)具有0边界条件,即有u(k)(0,t)=0,(k=0,1,…,n-1),且a=0,则式(3)可变为
式(10)变为
(11)
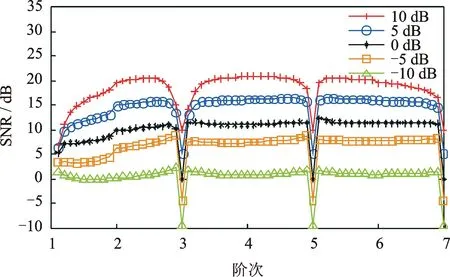
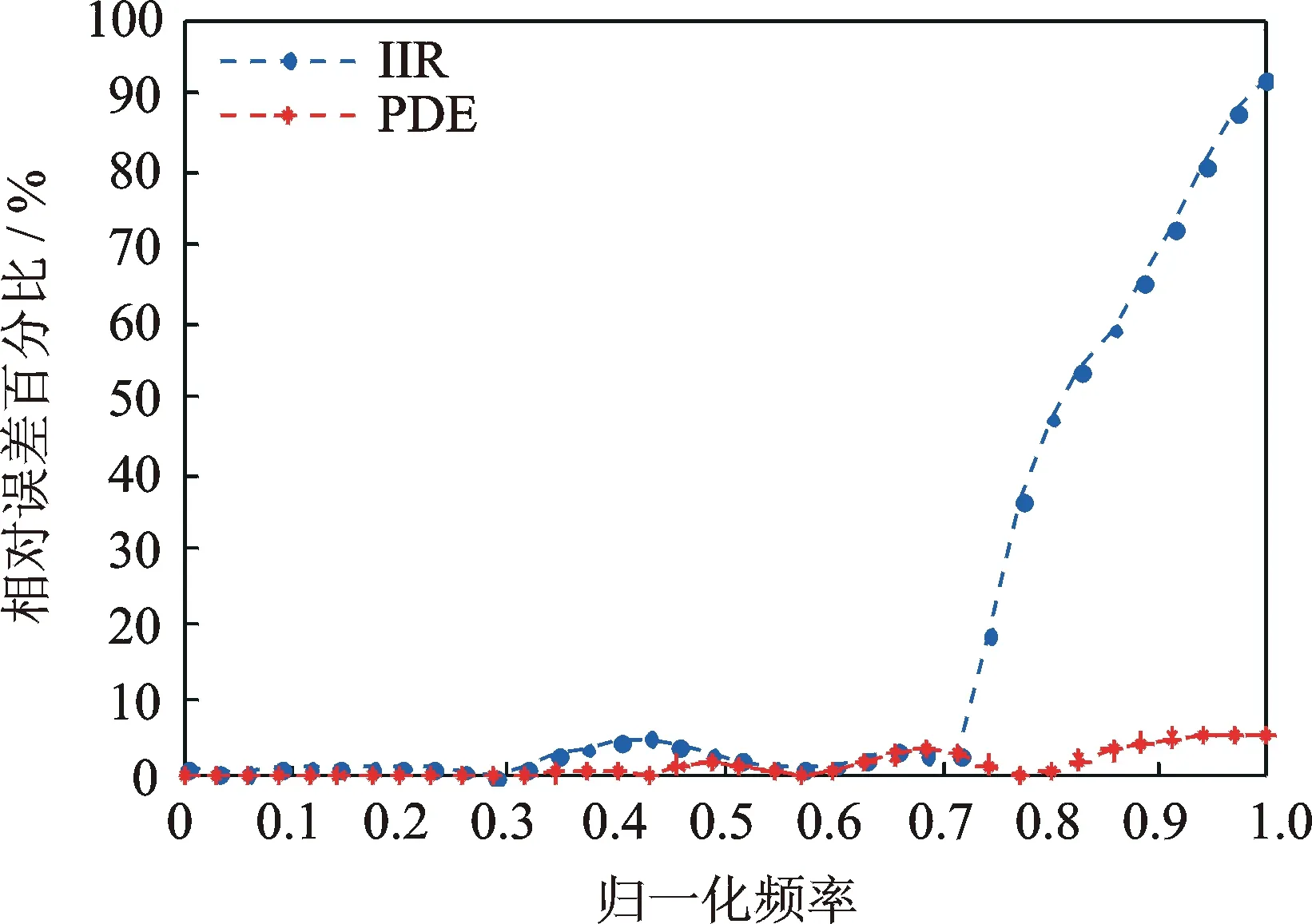
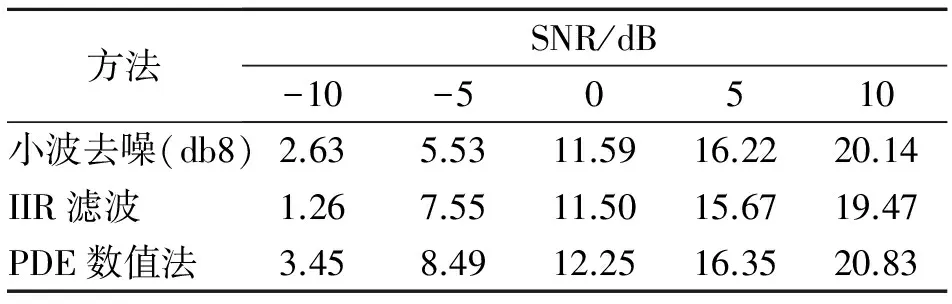
其中:x∈R;t>0;n∈Z;v=r+n;0 此时 (12) 若v>0时,K(ω,t)为低通滤波器;若v<0时,为高通滤波过程。阶次越高,滤波器衰减的越快。不同阶次对应的滤波器幅频特性如图1所示。 图1 滤波器幅频特性Fig.1 Filter magnitude-frequency curves 1.3 PDE滤波器参数确定 设Y为滤波器截止频率对应的衰减,由式(12)得到 即 (13) 其中:τ为演化时间。 由式(13)可知,当阶次v及a确定后,通过确定滤波范围即可确定演化时间。当v>0时,若截止频率无穷大,τ趋近于0,此时输入信号相当于通过了一个全通滤波器;而当截止频率趋近于0,τ趋近于无穷大,PDE滤波后输出直流;当v<0时,情形与v>0相反。 对于式(7),任意阶PDE滤波器系数k(x,t)可以通过经典的滤波器设计方法得到, 则滤波后的信号为φ′(x)=φ(x)*k(x,t)。然而在滤波器数值化及截断过程中,实际PDE滤波器与理想PDE滤波器之间存在差异。因此,通过对分数阶PDE的数值化求解可更准确地实现PDE滤波。 当n=1时,阶次1≤v<2, 式(11)变为 (14) 将u(x,t)变量分别替换成t和τ,将t和τ离散,并根据中心差分法、向后Euler格式和式(1),式(14)变为 (15) (16) (17) 式(16)变为 即 (18a) 记C={c1,c2,…,cm,cm+1,cm+2},其中c1=-qg0,c2=-qg1+1。当3≤j≤m+1,cj=-q(gj-1-gj-3),cm+2=qgm-1,则 (18b) (19a) (19b) 式(18)可以记为 (20) 式(15)中,分数阶微分方程向后Euler格式迭代过程对网格比q没有限制[17]。对于式(19),当演化步长l=τ,总的迭代次数s=τ/l=1,即形成了PDE降噪的快速算法。 (21) 输入噪声信号u0,截止频率为fn,采样频率为fs,PDE阶次为v。输出降噪后信号u。任意分数阶PDE降噪算法如下: 2) 根据PDE的阶次v、采样频率fs和截止频率fn计算网格比q; 3) 根据gb和网格比q计算集合C; 4) 计算矩阵A并得到滤波矩阵A-1; 5) 得到降噪后信号u。 3.1 不同阶次降噪性能比较 图2(a)为频率分别为5,7,9,10和20 Hz的正弦信号叠加而成的仿真信号,各信号分量的幅值为1 V。对该信号分别叠加不同信噪比的高斯白噪声(信噪比分别为-10,-5,0,5和10 dB),采样频率为1 kHz,取1 000个采样点进行降噪对比实验。其中,图2(b)为信噪比为-10 dB的高斯白噪声。 图2 仿真信号Fig.2 The simulation signal 图3为降噪效果随阶次变化曲线。从图3中可以看出,随着阶次的增大,信噪比并未呈单调增加,在4阶附近获得较好的降噪效果。这是因为在滤波器设计过程中,应根据噪声信号的类型不同,合理设置滤波器通带截止频率和阻带截止频率。对于本研究的仿真信号,由于噪声为宽带噪声,当阶次较高时,虽PDE滤波器符合优良滤波特性要求,但低频噪声将会更多地保留,从而降低了滤波效果。所以信噪比并未呈单调增加,而是在4阶附近获得较好的降噪效果。当为奇次阶时,PDE滤波器幅频特性为1,滤波前后信号幅频特性不变,因此信噪比不变,且奇次阶附近阶次降噪效果较差。 图3 降噪效果(SNR)随阶次变化图Fig.3 Noise reductions (SNR) with different order 为了对比实际滤波器跟理想滤波器之间的差异,定义相对误差百分比A为 (22) 其中:B为实际值;C为理论值。 图4为IIR数字滤波器和PDE滤波器的相对误差百分比对比图。其中,IIR数字滤波器和PDE滤波器的参数相同,通带截止频率为35Hz,阻带截止频率为67Hz,PDE滤波器的阶次为4。从图4可以看出,IIR数字滤波器的误差比PDE滤波器要高且波动大,PDE实际滤波器与理论滤波器之间的差异很小。 图4 IIR数字滤波器与PDE滤波器的相对误差对比图Fig.4 The percentage absolute relative error of IIR filter and the proposed PDE filter 3.2 与其他降噪方法的比较 采用小波去噪、IIR数字滤波以及4阶PDE差分求解去噪等方法分别对不同信噪比的仿真信号进行去噪分析。表1为不同滤波方法下降噪效果的对比。 表1 不同滤波方法下的降噪效果 表1中,小波去噪的小波基为db8,分解层数为5,阈值函数为软阈值,表中IIR滤波采用的是3阶巴特沃斯数字滤波器。根据图3,选择4阶PDE进行比较。其中,IIR数字滤波器法、PDE差分求法的截止频率为35 Hz。从表1看出,在信噪比较大时,小波方法和PDE差分方法具有相近的降噪效果(>5 dB);而信噪比较低时,PDE差分方法有较明显的降噪效果(-5 dB)。在实际应用中,小波去噪过程复杂,需要根据信号的特点选择不同的小波基、阈值函数等。图5为对信号比SNR=5 dB的信号降噪比较。另外,从图5(c)中可以看出,IIR数字滤波会产生时移(红色标记)。 图5 不同方法的降噪效果图Fig.5 Noise reduction of different filtering methods 表2为几种去噪方法的时间性能比较。 CPU为Intel(R) Core(TM) i3,主频为2.27GHz,内存为4GB,每个方法运行8次,剔除最高和最低值,求剩余6次平均运行时间。 表2 时间性能比较 从表2可以看出,几种去噪方法中IIR 滤波、PDE数值求解耗时相当,小波降噪方法耗时最长。 3.3 现场应用 轴心轨迹作为转子振动信号的一类重要图形征兆,其形状和动态特性包含了丰富的故障征兆信息。然而在现场实际测量的振动信号中往往都会受到噪声污染,轴心轨迹非常复杂,不易获得清晰的特征。因此,对轴心轨迹降噪成为转子特征提取的关键之一。图6是在重庆大学测试中心的转子实验台现场实验图。 图6 现场实验图Fig.6 Field experiment 图7(a)和7(b)分别为转轴原始轴心轨迹图和使用PDE降噪之后的轴心轨迹图。其转子转速为6 970 r/min,采样频率为1 652 Hz。从图7(a)中可以看出,原始轴心轨迹较混乱。如图3所示,PDE滤波器在阶次4附近区域的降噪效果相近,为了方便PDE滤波的数值计算,图7(b)PDE降噪阶次选取整数阶次4,PDE降噪的截止频率为85 Hz。由图7可以看出,该轴的轴心轨迹为椭圆形,表明该轴存在严重的不平衡,而其他故障很小。 图7 滤波前后的轴心轨迹图Fig.7 Original and PDE filtered shaft centerline orbits PDE在图像滤波、修补和增强等方面都取得了很好的效果。将PDE用于一维信号的降噪处理的研究才刚刚起步,主要集中在整数阶的降噪方法。笔者从滤波器设计的角度,提出了任意阶PDE滤波器统一模型,研究了PDE滤波的两种数值化过程,建立了基于数字差分求解的降噪一般过程,分析了阶次对降噪性能和时间性能的影响。通过仿真信号对小波阈值去噪,IIR数字滤波降噪及PDE数值求解降噪等多种去噪方法进行了对比分析。实验表明,分数阶PDE数值求解去噪方法算法简单,效果良好,是一种有效的信号去噪方法。 [1] 钱征文,程礼,李应红.利用奇异值分解的信号降噪方法[J]. 振动、测试与诊断,2011(4):459-463. Qian Zhengwen, Cheng Li, Li Yinghong. Noise reduction method based on singular value decomposition[J]. Journal of Vibration, Measurement & Diagnosis, 2011(4):459-463. (in Chinese) [2] Donoho D L. De-noising by soft-thresholding information theory[J]. IEEE Transactions on , 1995,41(3):613-627. [3] 秦毅,王家序,毛永芳.基于软阈值和小波模极大值重构的信号降噪[J]. 振动、测试与诊断,2011(5):543-547. Qin Yi, Wang Jiaxu, Mao Yongfang. Signal denoising based on soft thresholding and reconstruction from dyadic wavelet transform modulus maxima[J]. Journal of Vibration, Measurement & Diagnosis, 2011(5):543-547. (in Chinese) [4] Dragomiretskiy K, Zosso D. Variational mode decomposition signal processing[J]. IEEE Transactions on, 2014,62(3):531-544. [5] 徐仁林,安伟.小波降噪在信号基于EMD的Hilbert变换中的应用[J]. 噪声与振动控制,2008(3):74-77. Xu Renlin, An Wei. Wavelet denoise application in the signal hilbert transform based on EMD[J]. Noise and Vibration Control, 2008(3):74-77. (in Chinese) [6] 张磊,彭伟才,原春晖,等.奇异值分解降噪的改进方法[J]. 中国舰船研究,2012(5):83-88. Zhang Lei, Peng Weicai, Yuan Chunhui, et al. An improved method for noise reduction based on singular value decomposition[J]. Chinese Journal of Ship Research, 2012(5):83-88. (in Chinese) [7] 刘艺柱,杨瑞兰.采用滑动平均滤波法提高硬币识别准确率的研究[J].制造业自动化, 2010(1):42-44. Liu Yizhu, Yang Ruilan. Moving average filtering method used to improve the accuracy of coins to identify research[J]. Manufacturing Automation, 2010(1):42-44. (in Chinese) [8] 杨柱中,周激流,晏祥玉,等. 基于分数阶微分的图像增强[J]. 计算机辅助设计与图形学学报,2008(3):343-348. Yang Zhuzhong, Zhou Jiliu, Yan Xiangyu, et al. Image enhancement based on fractional differentials[J]. Journal of Computer-Aided Design & Computer Graphics, 2008(3):343-348. (in Chinese) [9] Machado B B, Goncalves W N, Bruno O M. Enhancing the texture attribute with partial differential equations: a case of study with Gabor filters[J]. Advanced Concepts for Intelligent Vision Systems, 2011,6915:337-348. [10]Baravdish G, Evangelista G, Svensson O, et al. PDE-SVD based audio denoising[C]∥Communications Control and Signal Processing (ISCCSP). Washington DC, USA: IEEE, 2012:1-6. [11]Yin Aijun, Zhao Lei, Yang Zhengyi, et al. Noise reduction method for vibration signals 2D time‐frequency distribution using anisotropic diffusion equation [J]. Mathematical Methods in the Applied Sciences, 2015,38(4):609-616. [12]尹爱军,王璇. PDE信号修补方法及在EMD端点效应处理中的应用[J]. 振动与冲击,2012(2):6-9,61. Yin Aijun, Wang Xuan. Signal restoring based on PDE and its application in end effect processing of EMD[J]. Journal of Vibration and Shock, 2012(2):6-9,61. (in Chinese) [13]Pu Yifei, Siarry P, Zhou Jiliu, et al. Fractional partial differential equation denoising models for texture image[J]. Science China-Information Sciences, 2014,57(7):1-19. [14]Bai J, Feng X C. Fractional-order anisotropic diffusion for image denoising[J]. Ieee Transactions on Image Processing, 2007,16(10):2492-2502. [15]蒲亦非. 分数阶微积分在现代信号分析与处理中应用的研究[D].成都:四川大学,2006. [16]Chen Changming, Liu F, Turner I, et al. A Fourier method for the fractional diffusion equation describing sub-diffusio[J]. Journal of Computational Physics, 2007,227(2):886-897. [17]El-Mikkawy M E A. On the inverse of a gene tridiagonal matrix[J]. Applied Mathematics and Computation, 2004,150(3):669-679. 10.16450/j.cnki.issn.1004-6801.2016.06.006 *国家自然科学基金资助项目(51105396); 中央高校基本科研业务费资助项目(CDJZR13 11 55 01) 2014-12-09; 2015-01-07 TN911 尹爱军,男,1978年5月出生。教授、博士生导师。主要研究方向为智能测试与虚拟仪器、现代信号分析处理及故障检测与诊断等。曾发表《Thermography spatial-transient-stage mathematical tensor construction and material property variation track》(《International Journal of Thermal Science》2014,Vol.85)等论文。 E-mail:aijun.yin@cqu.edu.cn
2 任意阶PDE降噪的数值化

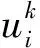

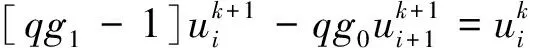


3 实验分析与应用





4 结束语


