基于流线模型的五点井网平面波及系数研究

冀中原 李江飞

(1. 中国石油天然气勘探开发公司， 北京 100034；2. 承德石油高等专科学校热能工程系， 河北 承德 067000)

基于流线模型的五点井网平面波及系数研究

冀中原1李江飞2

(1. 中国石油天然气勘探开发公司， 北京 100034；2. 承德石油高等专科学校热能工程系， 河北 承德 067000)

根据达西定律及水电相似原理，建立了水驱油流线模型，推导出均质地层条件下五点井网的油水前缘分布计算公式，并通过数值计算得到水驱波及系数与时间的关系。研究表明，在流线模型条件下，五点井网的水驱波及系数随时间的变化呈先快速上升后逐渐变缓的趋势。

流线模型； 五点井网； 波及系数； 水驱前缘

在均质油藏水驱开发过程中，平面波及系数是评价油藏开发效果和进行动态分析的重要指标。目前学者对于平面波及系数的研究较多，研究方法主要有实验、油藏理论推导和数值模拟方法[1-2]。张丽华等人曾运用数值模拟的方法计算油藏水驱波及系数[3]。范江等人运用概率论和量纲分析方法建立了非均质油层波及系数计算模型[4]。郭粉转等人推导了考虑启动压力梯度的四点井网、五点井网、反九点井网和菱形反九点井网平面波及系数计算公式[5-8]。齐亚东等人运用流管积分法，推导了特低渗透油藏三角形井网平面波及系数计算公式[9]。何聪鸽通过构建考虑启动压力梯度的非达西流管模型，利用坐标变化将渗透率各向异性油藏转化为等效各向同性油藏，推导了特低渗透各向异性油藏五点井网油井见水时间和平面波及系数的计算公式[10]。这些现有模型均基于流管理论来研究平面波及系数。本次研究中建立了均质地层流线模型，在其基础上推导出均质地层条件下的井网水驱面积波及系数计算公式，拟为均质油藏五点井网水驱开发调整提供理论依据。

1 基于流线模型的平面波及系数

1.1 模型条件假设

通过研究不同井网模式下流动单元的水驱波及系数，研究不同面积井网的水驱波及系数。图1所示为五点井网、反九点井网流动单元示意图。

图1 五点井网、反九点井网流动单元示意图

流线模型满足以下条件假设：

(1) 流动介质为均质地层，油水渗流满足达西定律。

(2) 流动区域由流线组成，以流线作为渗流流动的研究单元，每一条流线等同于一根极细的管道，管中流动方式为水驱油活塞驱，不考虑重力和毛管力。

(4) 对于相同流体，每条流线(折线)的渗流阻力与等长度直线段的流动阻力相同。

(5) 地层表现为均质，且驱动方式为活塞驱，即kw=ko=k。

1.2 平面波及系数计算方法

1.2.1 油水前缘位移公式推导

对于△ABD，假设井距AB=l。由正弦定理得到公式(1)：

(1)

式中： α —— 注入井角变量，(°)；

β —— 生产井角变量，(°)。

图2 流线模型示意图

由式(1)可得式(2)：

(2)

对于任意一条流线，可将其转化为图3所示的等长度直线段。

图3 流线示意图

由达西定理可知，任一条流线的渗流速度为：

(3)

式中：v—— 渗流速度，ms；

μo—— 地层原油黏度，mPa·s；

μw—— 注入水地下黏度，mPa·s；

ph—— 注入井井底压力，MPa；

pf—— 生产井井底压力，MPa。

油水前缘的位移与油水前缘的移动速度的关系满足式(4)：

(4)

联立式(3)、(4)可得式(5)：

(5)

将式(5)代入式(4)可得式(6)：

(6)

1.2.2 五点井网水驱波及系数计算

(7)

图4 五点井网流线示意图

当α=0时：

计算可得：

Δp=ph-pf

计算可得：

当α=π4时：

计算可得：

计算可得：

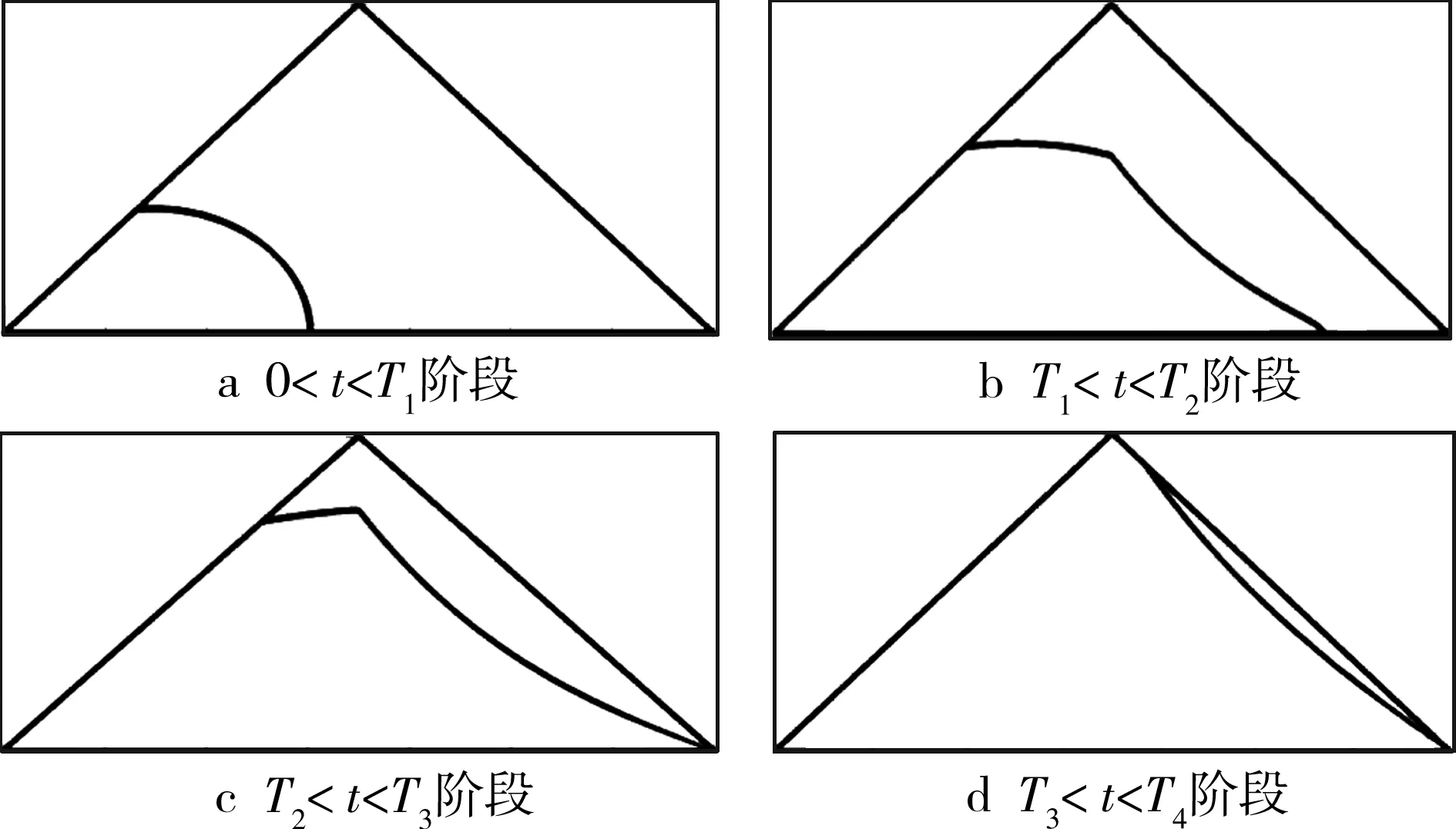
将水驱油的过程分为4个阶段，0

(1) 计算0

图5 油水前缘分布(0

水相波及区域为扇形AFPE，油水前缘为曲边FPE，所有流线的水驱前缘均未到达该流线的拐点，水相线段尚未发生弯折。APQB为其中一条流线，∠PAB=α。线段AP表示水相，折线PQB表示油相。

水相波及区域面积为S波及1：

(8)

波及系数EA1：

(9)

将式(7)代入式(8)，通过数值求解方法可得到0

(2) 计算T1

图6 油水前缘分布(T1< t< T2阶段)

水相波及区域为多边形AFDQEA，油水前缘为曲边FDQE。在扇形AFD区域内，油水前缘尚未到达该流线的拐点；在多边形ADQEA区域内，油水前缘已经过该流线的拐点，但尚未到达油井B点。APQB为其中任一条流线轨迹，令∠PAB=α，∠PBA=β，∠DAB=α1，∠DBA=β1。其中α=β，α1=β1。

对于△ADB，由正弦定理可得到公式(10)：

(10)

将式(7)代入式(10)可得到公式(11)：

(11)

扇形AFD的面积为

折线APB的长度为

lAPB=l×sec α=l×sec β

所以扇形BDQE的面积计算公式为：

(12)

水驱波及区域面积计算公式为：

(13)

波及系数计算公式为：

(14)

将式(7)代入式(13)，通过数值求解方法可得到T1

(3)计算T2

图7 油水前缘分布(T2< t

水相波及区域为多边形AFDQBA，油水前缘为曲边FDQE。在扇形AFD区域内，油水前缘尚未到达拐点；在多边形ADQBHA区域内，油水前缘已经过该流线的拐点，但尚未到达油井B点；在三角形AHB区域内，油水前缘已到达油井B点。可知线段BH与弧线DQB在B点相切。APQB为其中任一条流线轨迹，令∠PAB=α，∠PBA=β，∠DAB=α2，∠DBA=β2，∠HAB=α3，∠HBA=β3。

对于△ADB，由正弦定理可得到公式(15)：

(15)

将式(7)代入式(15)可得到公式(16)：

(16)

对于△AHB，由正弦定理可得到公式(17)：

(17)

将式(7)代入式(17)可得到公式(18)：

(18)

同上，可得水驱波及面积：

(19)

得波及系数：

(20)

将式(7)代入式(19)，通过数值求解方法可得到T2

(4)计算T3< t

图8 油水前缘分布(T3< t

水相波及区域为多边形AOFQB，油水前缘为曲边FQB。在多边形AOFBHA区域内，油水前缘已经过该流线的拐点，但尚未到达油井B点；在三角形AHB区域内，油水前缘已到达油井B点。可知线段BH与弧线FQB在B点相切。APQB为其中任一条流线轨迹，令∠PAB=α，∠PBA=β，∠HAB=α3，∠HBA=β3。

对于△AHB，由正弦定理可得：

(21)

将式(7)代入式(21)可得：

(22)

可计算水驱波及区域面积：

(23)

得波及系数：

(24)

将式(7)代入式(23)，通过数值求解方法可得到T3

2 实例应用

海上某油田物性参数如下：注水井压力ph为160×105Pa，pf为160×105Pa；油相黏度μo为78 mPa·s，水相黏度μw为1 mPa·s；介质对油相和水相的渗透率kw、ko均为2.2 μm2；油水井井距为350 m。

根据物性参数可求出：T1=204 456 676 s≈6.48 a，T2= 274 928 977 s≈8.72 a，T3= 4 089 133 41 s≈12.97 a，T4= 549 948 343 s≈17.44 a。图9所示为水驱平面波及系数与时间的关系曲线。

图9 水驱平面波及系数与时间关系曲线

分别对以上4个阶段中某一时刻的油水前缘分布进行对比，可以看出各阶段油水前缘分布的区别(见图10)。

图10 4个阶段的油水前缘分布示意图

3 结 语

本次研究中建立了均质地层水驱开发的流线模型，通过达西定律和水电相似原理推导出五点井网

流动单元的水驱前缘分布计算公式。通过编写程序计算出不同时间段流动单元内的水驱波及面积与波及系数，五点井网的水驱波及系数随时间的变化呈现先快速上升后逐渐变缓的趋势。该方法可以为五点井网的开发设计和评价提供参考。

[1] 程林松.高等渗流力学[M].北京:石油工业出版社，2011:287-299.

[2] 李金宜，戴卫华，罗宪波，等.海上油田波及系数修正新方法[J].中国海上油气,2012,24 (10):86-89.

[3] 张丽华，郎兆新.用数值方法研究面积井网系统的扫油效率[J].石油大学学报(自然科学版)，1988，12(3)：86-97.

[4] 范江，张子香，扎拉杜新A B.非均质油层波及系数计算模型[J].石油学报，1993，14(1)：92-97.

[5] 郭粉转，唐海，吕栋梁，等.渗流启动压力梯度对低渗透油田四点井网面积波及效率影响[J].大庆石油学院学报，2010，34(1)：33-38.

[6] 郭粉转，唐海，吕栋梁，等.渗流启动压力梯度对低渗透油田五点井网面积波及效率影响[J].大庆石油学院学报，2010，34(3)：65-68.

[7] 吕栋梁，唐海，郭粉转，等.低渗透油田反九点井网面积波及效率影响研究[J]．西南石油大学学报(自然科学版)，2012，34(1)：147-153．

[8] 朱圣举，朱洁，安小平，等.低渗透油藏菱形反九点井网面积波及系数研究[J].重庆科技学院学报(自然科学版)，2013，15(2)：80-83.

[9] 齐亚东，雷群，杨正明，等.低渗透断块不规则三角形井网有效动用系数计算及应用[J].中南大学学报(自然科学版)，2012，43(3)：1065-1071.

[10] 何聪鸽，范子菲，方思冬，等.特低渗透各向异性油藏平面波及系数计算方法[J].油气地质与采收率，2015,22(3)：77-83.

Study on Areal Sweep Efficiency of Five-Spot Well Pattern Based on Streamline Model

JIZhongyuan1LIJiangfei2

(1. China National Oil and Gas Exploration and Development Corporation, Beijing 100034, China;2. Department of Thermal Engineering in Chengde Petroleum College, Chengde Hebei 067000, China)

Based on Darcy law and similarity principle of water and electricity, the streamline model of water displacing oil was built. On this basis, we calculated the water flooding frontier of five-spot well pattern under the condition of homogeneous reservoir; and furthermore, the relationship between the areal sweep efficiency and time was obtained by numerical calculation. The study shows that the areal sweep efficiency of five-spot well pattern starts steep and later flattens.

streamline model; 5-spot well pattern; sweep efficiency; water flooding frontier

2016-03-15

国家科技攻关计划基金资助项目“大型油气田及煤层气开发”(2011ZX05044)

冀中原(1988 — )，男，硕士，工程师，研究方向为油藏开发。

TE312

A

1673-1980(2016)06-0036-05