局域能量逐层提取的LMD模态混叠抑制方法

郭 枫

(中国人民解放军91550部队94分队，辽宁 大连 116023)

【基础理论与应用研究】

局域能量逐层提取的LMD模态混叠抑制方法

郭 枫

(中国人民解放军91550部队94分队，辽宁 大连 116023)

提出了一种基于局域能量逐层提取的局域均值分解(Local Mean Decomposition,LMD)模态混叠抑制方法。对待分析信号利用LMD得到一系列乘积函数(Product Function，PF)，对各PF的能量进行积分，根据积分比值确定模态混叠导致的能量泄漏程度，并从具有模态混叠的高阶PF中移除下一阶PF的成分构成新的PF，从原始信号中减去新的PF得到新的待处理信号，继续执行LMD，直到所有PF频率成分各自独立，从而实现对模态混叠的抑制。仿真结果表明：算法可以有效抑制小频率比混合信号导致的模态混叠，在实际工程上具有一定推广应用价值。

LMD；PF；模态混叠；局域能量

以傅里叶变换为基础的经典谱估计方法在非平稳信号处理中表现出不足[1]，为了能够揭示非平稳信号内蕴的物理过程，时频分析技术得到了人们的重视。近年来，以局域均值分解(Local Mean Decomposition,LMD)和经验模态分解(Empirical Mode Decomposition，EMD)为基础的局域波分析方法[2-3]得到了人们的重视，局域波分析方法从瞬时频率概念出发，在将非平稳信号分解为系列单分量后，利用希尔伯特谱给出信号的时频表示结果，从而打破了不确定性原理的约束，具有非常好的时频聚集性能。但是，到目前为止，LMD和EMD的数学理论基础尚不完备，在分解过程中都承受端点效应和模态混叠问题的影响。LMD是S.S.jonathan首先提出的一种将信号分解为乘积函数(Product Function, PF)的方法[4]，类似于EMD但是又不同于EMD。两者最主要的区别是，EMD将信号分解为一系列具有隐含物理意义的IMF，而LMD将信号分解为一系列幅度函数与瞬时频率表示的PF。从两者的适用性来说，EMD更适用于瞬态信号或者是多个频率较为稳定的单分量组成的多分量信号，而LMD更适用于具有调频信号特征的单分量组成的多分量信号[5]。当待处理信号中含有小频率比信号的多个单分量或者是在信号中具有间歇性高频弱信号干扰时，EMD会产生模态混叠[6-7]，即同一阶IMF中含有多个分量的信息。实际应用中发现，上述情况也会导致LMD产生模态混叠。由于局域波分析方法在信号分解后利用希尔伯特谱进行分析，而希尔伯特谱仅适用于单分量信号，模态混叠的存在导致瞬时频率求解的错误，从而模糊了以局域波为基础的时频表示结果。针对LMD模态混叠问题，相关研究人员将EMD模态混叠抑制的方法应用于LMD方法中，证明同样具有良好的模态混叠抑制性能，如文献[8]提出的总体局域均值分解法，可以有效解决间歇性高频弱信号干扰导致的模态混叠问题。但是对于含有小频率比的多个单分量组成的多分量信号在LMD分解过程中产生模态混叠问题，目前尚未见相关文献报道。而该类信号在工程上广泛存在，典型的如飞行器试验中的遥测高低频振动信号、冲击信号等。本文针对LMD在处理含有小频率比单分量信号的多分量信号时的模态混叠现象进行了分析，提出了一种基于局域能量逐层提取的LMD方法，首先利用LMD得到一系列PF，对各PF的能量进行积分，根据积分比值确定模态混叠导致的能量泄漏程度，并从具有模态混叠的高阶PF中移除下一阶PF的成分构成新的PF，从原始信号中减去新的PF得到新的待处理信号，继续执行LMD，直到所有PF频率成分各自独立，从而实现对模态混叠的抑制，最后用仿真信号对文中提出的方法进行了验证，证明了算法的有效性。

1 LMD与模态混叠

作为局域波的一种实现方法，LMD不需要固定的基函数，是一种自适应的信号分解方法。通过LMD可以将多分量信号分解为一系列乘积函数PF，每个乘积函数PF为一个包络信号和一个纯调频信号的乘积[9]。如果每个PF均满足单分量条件，那么在此基础上进行瞬时频率求解才有意义。LMD的具体实现步骤可以总结如下[10-11]：

1) 首先确定原始信号x(t)所有局部极值点，包括极大值点和极小值点，n11(kl)(l=1,2,…,M)，分别根据式(1)和式(2)求得局部幅值m11(t)和局部均值a11(t)。

(1)

(2)

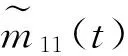
(3)

(4)

3) 如果s11(t)不是一个区间[-1,1]上的纯调频信号，则将s11(t)作为原始信号重复n次步骤1)和2)的操作，直到满足要求为止，瞬时相位和瞬时频率可以由式(5)和式(6)给出。

φ1(t)=arccos(s11(t))

(5)

(6)

4) 所有局部幅值的乘积得到瞬时幅值

(7)

而首个函数乘积可以由式(8)给出

PF1(t)=a1(t)s1n(t)

(8)

5) 将第一个PF分量从原始信号中分离出来

u1(t)=x(t)-PF1(t)

(9)

得到新的信号u1(t)作为原始信号重复步骤1)～4)，重复k次，直到所有uk(t)都满足单调函数，至此，原始信号可以表示为k个PF分量与一个单调分量的和

(10)

如果LMD能够完全分解，即分解所得到的PF为纯调频信号与幅度信号乘积，则瞬时幅值和瞬时频率可以准确获得，那么可以在LMD的基础上进行时频分析，获得采集得到的观测信号的时域和频域局域化信息。如果多分量信号中两个单分量成分频率非常接近，那么在LMD过程中将会产生模态混叠，在具有模态混叠的PF分量上求解瞬时相位和瞬时频率都会产生无法解释的结果。

以仿真信号为例说明LMD的模态混叠， 仿真信号由3个中心频率不同的正弦信号组成，采样频率fs=2 000 Hz，正弦信号中心频率分别为f1=100 Hz、f2=60 Hz和f3=15 Hz。

x(t)=5sin(2πf1t)+3sin(2πf2t)+sin(2πf3t)

(11)

仿真信号时域波形和LMD分解结果如图1所示，对应的仿真信号和各PF的频谱如图2所示。

从图1和图2中可知，LMD分解得到的第一阶PF存在着严重的模态混叠，即第一阶PF分量中含有第二阶PF的成分，同时LMD得到了两个虚假分量，这是由于分解过程中插值和拟合导致的能量泄漏，在实际处理中可以去掉虚假分量，因为能量泄漏产生的虚假分量量级很低。但是第一阶PF的模态混叠将导致第一阶PF无法直接求取瞬时相位和瞬时频率，而第二阶PF由于部分信息被分解到第一阶PF之中，能量泄漏严重，本来为3的能量幅值仅剩0.5左右在第二阶PF中，这直接导致对第二阶PF进行希尔伯特谱幅值求解时产生歧义。因此，在进行时频分析之前必须消除该模态混叠。

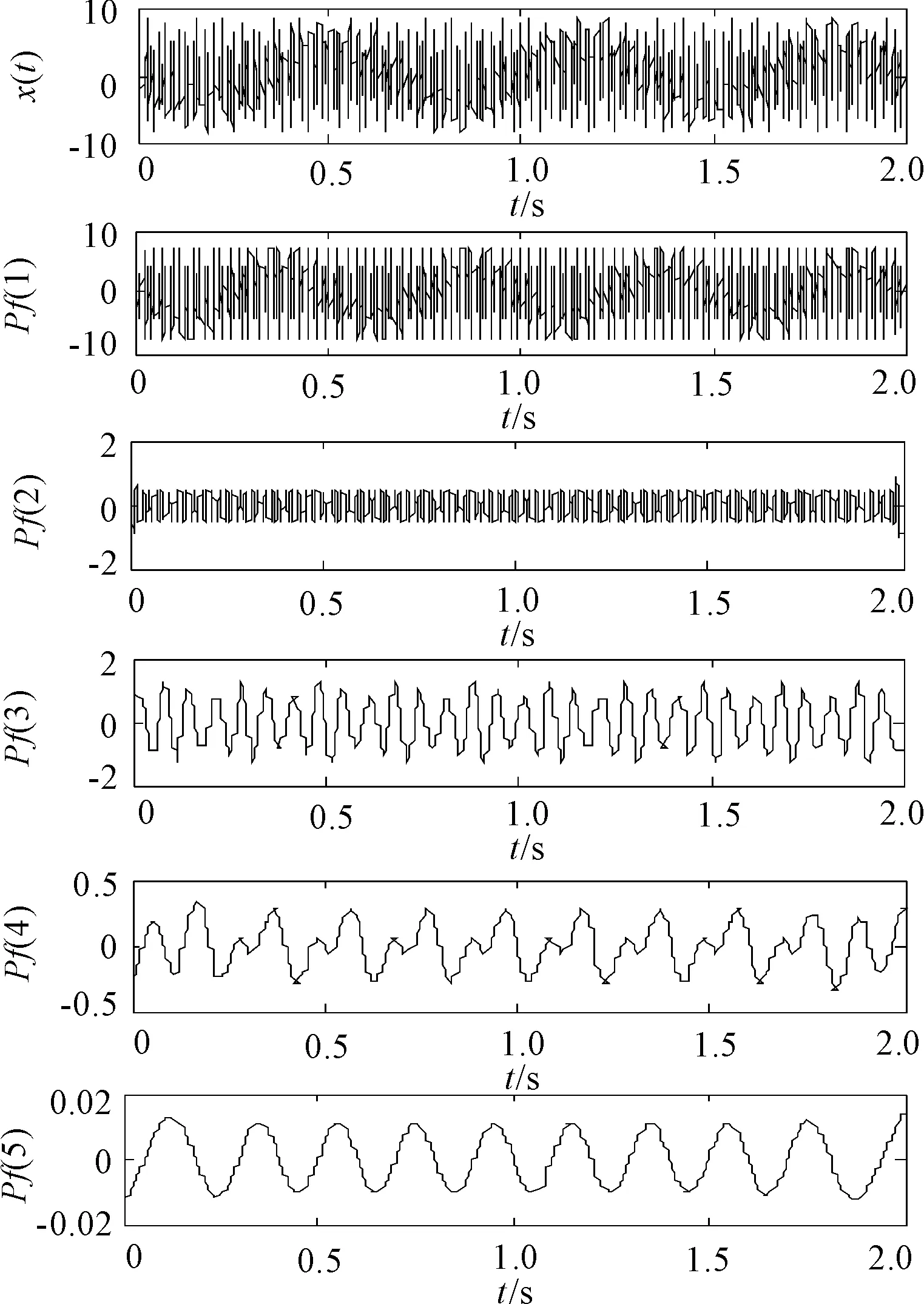
图1 LMD分解结果

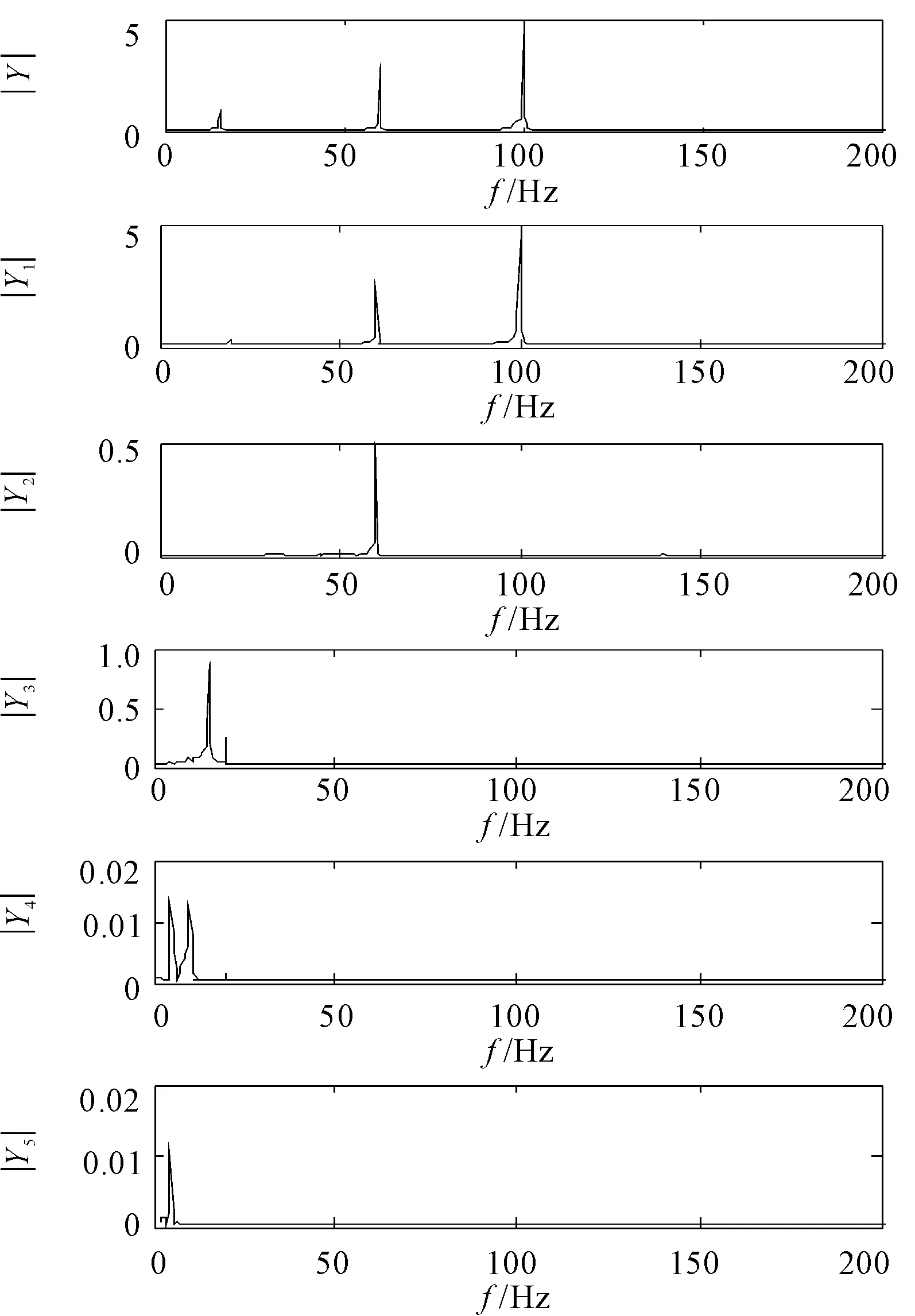
图2 信号和PF频谱

2 局域能量逐层提取的LMD方法

既然LMD在信号处理过程中获得的PF是依频率划分的，那么可以认为LMD同EMD类似，是一种多尺度筛分方法，即在频率上从高到低分解得到各PF。对于EMD而言，其分解尺度在对数频率域上是均匀尺度划分的，但是对于LMD，该分解尺度规律尚未得到验证。模态混叠产生原因可以理解为LMD在信号的分解过程中分解尺度受限，导致相邻频率间能量串扰，因此从模态混叠的PF中移除相邻阶次的PF可以消除模态混叠。根据这一思想，给出一种局域能量逐层提取的LMD方法，具体实现步骤如下：

1) 设待分析多分量信号为x(t)，将x(t)进行LMD分解得到一系列PF。

2) 对x(t)和每个PF分别做傅里叶变换，观察每个PF中包含的频率信息内容，并依据设定的尺度a(f)对频域进行划分，所选尺度a(f)根据各PF覆盖的频率范围而定。

3) 按照尺度a(f)对各阶尺度范围内的x(t)的频谱进行积分，获得局域能量幅值Ai，同时对各PF进行频域积分，获得局域能量幅值Bi。

4) 在频率域判别最低阶次的模态混叠PF，其相邻下一阶次PF的局域能量设为Bj，将其与x(t)对应尺度的局域能量Aj进行比较，即λj=Aj/Bj，λj反映了相邻阶次能量泄漏的严重程度，则从模态混叠的PF中减去用局域能量比值修正的下一阶PF，可以消除模态混叠，模态混叠PF相邻的最低阶次PF利用该比值直接修正，即：

(12)

(13)

利用式(12)修正了Cj(t)的幅度，利用式(13)从Cj-1(t)中移除了Cj(t)的成分，从而实现对模态混叠的抑制。

5) 设

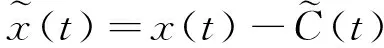
(14)

3 仿真分析

以式(11)给出的仿真信号进行处理来验证文中提出方法的有效性。

由图2可以看出，对于仿真信号进行第一次LMD后，第一阶PF具有模态混叠，其包含了第二阶PF的成分，在频率域设尺度为60Hz，求得局域能量积分比为6.0，则对第二阶PF分量乘以6进行幅值修正，对第一阶PF减去2.4倍的第二阶PF，移除第一阶PF中包含的第二阶PF信息，从而消除掉模态混叠。利用文中提出方法最终获得的LMD结果和对应的频谱分别如图3和图4所示。从图3可以看出，PILMD方法得到PF在时域波形上已经消除了模态混叠的影响，对应的频谱如图4也表明在第一阶PF中仅仅含有少量的相邻第二阶PF成分，对后续的时频处理影响可以忽略，因此证明文中提出的局域能量逐层提取改进的LMD方法在处理含有小频率比单分量的多分量信号时，可以有效地抑制模态混叠，获得较为理想的分解结果。

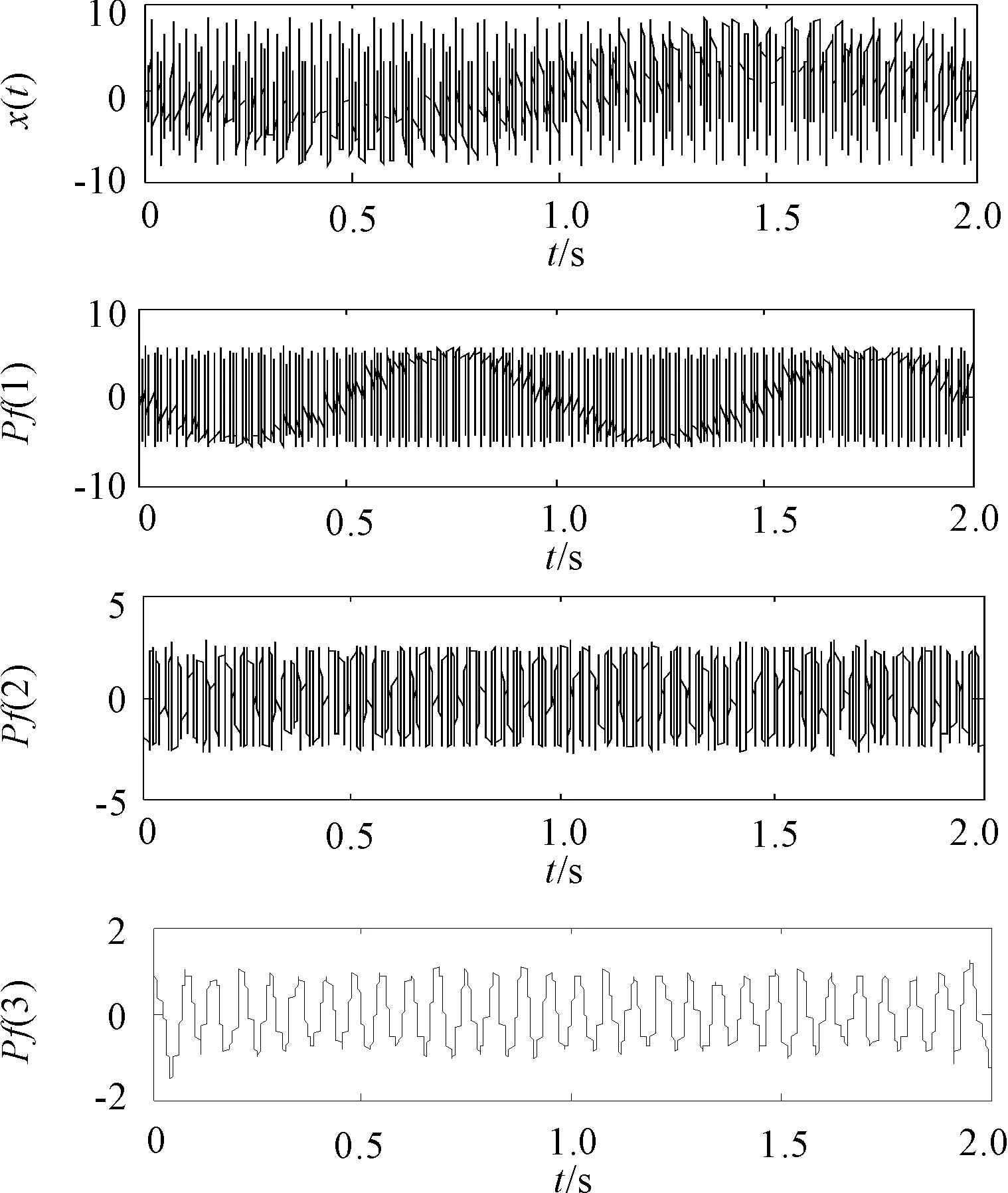
图3 改进LMD分解结果

图4 改进LMD的PF频谱

4 结论

本文通过对LMD模态混叠的分析，提出了依据频率域尺度划分的局域能量逐层提取改进LMD方法，通过相邻阶次PF耦合信息的逐层提取，有效改善了LMD模态混叠，使分解得到的各阶次PF具有了单分量性质，为后续时频分析奠定了基础。但是，LMD产生模态混叠的原因以及数学解释，有待于进一步的研究。

[1] 李振兴.细化FFT的短时傅立叶变换方法[J].四川兵工学报,2010,31(2):133-135，141.

[2] 李琳,张永祥,明延锋.改进的LMD方法及其在滚动轴承故障诊断中的应用研究[J].振动与冲击.2016,35(8):183-186.

[3] 黎恒,李智,莫玮.低采样率下经验模态分解性能提升研究[J].振动与冲击,2016,35(17):185-190.

[4] 王衍学,何正嘉,訾艳阳，等.基于LMD的时频分析方法及其机械故障诊断应用研究[J].振动与冲击,2012,31(9):9-12.

[5] SMITH J.S.The local mean decomposition and its application to EEG perception data[J].Journal of Royal Society Interface,2005(2):443-454.

[6] 肖瑛,殷福亮.解相关EMD:消除模态混叠的新方法[J].振动与冲击,2015,34(4):25-29.

[7] 徐冠雷,王孝通,徐晓刚，等.多分量到单分量可用EMD分解的条件及判据[J].自然科学进展,2006,16(10):1356-1360.

[8] 李慧梅,安钢,黄梦.总体局域均值分解法在坦克变速箱滚动轴承故障诊断中的应用[J].装甲兵工程学院学报,2013,27(2):37-42.

[9] 程军圣,杨怡,杨宇.基于LMD的能量算子解调机械故障诊断方法[J].振动、测试与诊断,2012,32(6):915-919.

[10]宋海军,黄传金,刘宏超，等.基于改进LMD的电能质量扰动检测新方法[J].中国电机工程学报,2014,34(10):1700-1708.

[11]杨武.基于LMD的AR模型在旋转机械故障诊断中的应用[D].大连:大连交通大学,2013.

[12]周颖涛，周绍骑，姚远航.减少模态混叠的改进 EEMD算法[J].重庆理工大学学报(自然科学)，2015(1):111-114.

(责任编辑唐定国)

LMD Mode Mixing Suppression Method by Layer Local Energy Extraction

GUO Feng

(Unit 94 of the No. 91550thTroop of PLA, Dalian 116023, China)

An improved algorithm based on local energy layer by local mean decomposition (LMD) layer extraction was proposed. The signal was decomposed to series Product Function (PF) by LMD and the local energy of each PF was obtained by integration. The leakage of energy level can be determined according to the local energy ratio, based on which the mode mixing component can be removed from the high order PF. The new PF was subtracted from the original signal and LMD was carried on repeatedly untill all the PF was obtained. The improved LMD can ensure that all PF frequency components are independent of each other, so as to realize the suppression of mode mixing. The simulation results show that the algorithm can effectively overcome the mode mixing caused by near frequency signal in the multicomponent signal, and it has certain application value in practical engineering.

LMD; PF; mode mixing; local energy

2016-07-22；

郭枫(1985—)，女，硕士，助理工程师，主要从事装备试验数据处理研究。

10.11809/scbgxb2016.12.035

郭枫.局域能量逐层提取的LMD模态混叠抑制方法[J].兵器装备工程学报，2016(12):155-158.

format:GUO Feng.LMD Mode Mixing Suppression Method by Layer Local Energy Extraction[J].Journal of Ordnance Equipment Engineering,2016(12):155-158.

P228.4

A

2096-2304(2016)12-0155-04

修回日期：2016-08-25