火炮回转质心对弹丸起始扰动的影响研究与优化

邹利波，顾克秋

(南京理工大学 机械工程学院,南京 210094)

【装备理论与装备技术】

火炮回转质心对弹丸起始扰动的影响研究与优化

邹利波，顾克秋

(南京理工大学 机械工程学院,南京 210094)

为了有效提高轻型牵引火炮射击精度，探索了火炮回转部分质心位置变化对弹丸起始扰动的影响规律;通过调节影响火炮回转部分质心位置的总体结构变量来间接改变质心位置，并在此基础上构建了火炮回转部分质心变化与弹丸起始扰动之间的参数化有限元模型;研究结果发现火炮回转部分质心位置变化对弹丸起始扰动具有较为明显的影响，在得到回转部分质心位置变化对弹丸起始扰动影响规律的基础上，利用遗传算法对火炮回转部分质心位置进行了优化，对指导火炮总体结构设计具有一定的指导意义。

回转部分质心；弹丸起始扰动；轻型火炮；优化

射击精度是衡量火炮性能的一个极其关键的技术指标之一，在满足射击稳定性的前提下，轻型火炮的总体结构参数的合理匹配会对弹丸起始扰动产生一定的影响。对火炮总体结构设计者而言，火炮的总体结构参数必须保证射击精度。轻型火炮作为当今火炮设计的趋势，在轻型火炮起落部分质心普遍前移的情况下，其质心位置对弹丸起始扰动究竟产生何种影响，尚不为人知。此外，面向火炮射击精度的结构设计文献很少，火炮总体结构参数对弹丸起始扰动的影响一直受到火炮结构设计者的高度关注[1]。本文尝试在国内已有研究工作的基础上，探索轻型火炮回转部分质心位置对弹丸起始扰动影响规律。

目前，研究火炮总体结构参数对火炮射击精度的工作不少，但尚未见轻型火炮回转部分质心位置变化对弹丸起始扰动影响规律的研究的有关报道。李强等[2]分析了后坐体滑块与摇架导轨间隙、前衬瓦与身管间隙、摇架高度等结构参数对弹丸起始扰动的影响规律，指出摇架臂板厚对弹丸起始扰动影响显著。梁传建等[3]研究了基于神经网络和遗传算法的火炮结构动力学优化，建立了火炮总体结构参数与炮口扰动之间的非线性映射关系。崔凯波等[4]建立了某型榴弹炮的虚拟样机模型，通过灵敏度分析获得了后坐体质量偏心、高低机弹簧刚度阻尼、土壤介质刚度阻尼对炮口扰动的影响程度，并在此基础上以减小炮口扰动为目标进行优化。葛建立等[5]基于ADAMS对某自行火炮总体结构参数进行灵敏度分析和优化。张俊飞等[6]建立了某牵引火炮刚柔耦合动力学有限元模型，考虑弹炮耦合作用，通过灵敏度分析获得火炮高、后大架尺寸和耳轴刚度阻尼等对炮口扰动的影响程度。彭迪[7]研究了针对大口径轻型火炮射击稳定性和全炮质量为目标的多目标优化，掌握了对轻型火炮重要总体结构参数匹配规律和主要设计参数。

综上所述，对于轻型火炮而言，由于其特殊的结构布局，回转部分质心位置对弹丸起始扰动有何影响，甚为人所知。本文在弹炮耦合全炮有限元模型的基础上，建立火炮回转部分质心位置与总体结构参数化弹炮耦合全炮动力学有限元模型，针对回转质心位置变化，设计不同方案研究其对弹丸起始扰动的影响。此外，在获得的规律基础上，对火炮回转部分质心变化进行了优化。

1 轻型火炮回转部分质心对弹丸起始扰动规律研究

1.1 弹炮耦合全炮动力学有限元模型

对于轻型牵引火炮独特的总体结构布局而言，合理的总体结构设计不仅可以提高火炮系统的射击稳定性，还可以提高射击精度。某轻型火炮总体结构示意图如图1所示，结构大致分为两大部分：起落部分(炮身、摇架、反后坐装置、平衡机)和炮架部分(上架、下架、高低机、方向机、炮轮悬挂装置)。轻型火炮回转部分包括起落部分、上架、高低机、方向机和上座圈等。

图1 轻型火炮结构示意图

按照有限元建模要求，在保证计算精度前提下对火炮部件建模进行合理设计及简化，并根据文献[2]中建立弹炮耦合动力学有限元模型的原理及要求，弹炮耦合有限元模型采用等参六面体减缩积分单元。为了提高计算精度，对单元采用了失真控制以及沙漏控制，忽略弹带的挤进过程和弹带所受挤进应力作用，将已刻好弹带划痕的弹丸装配至弹丸完全挤入膛线的初始位置[8]。建立的弹炮耦合动力学有限元模型如图2所示。

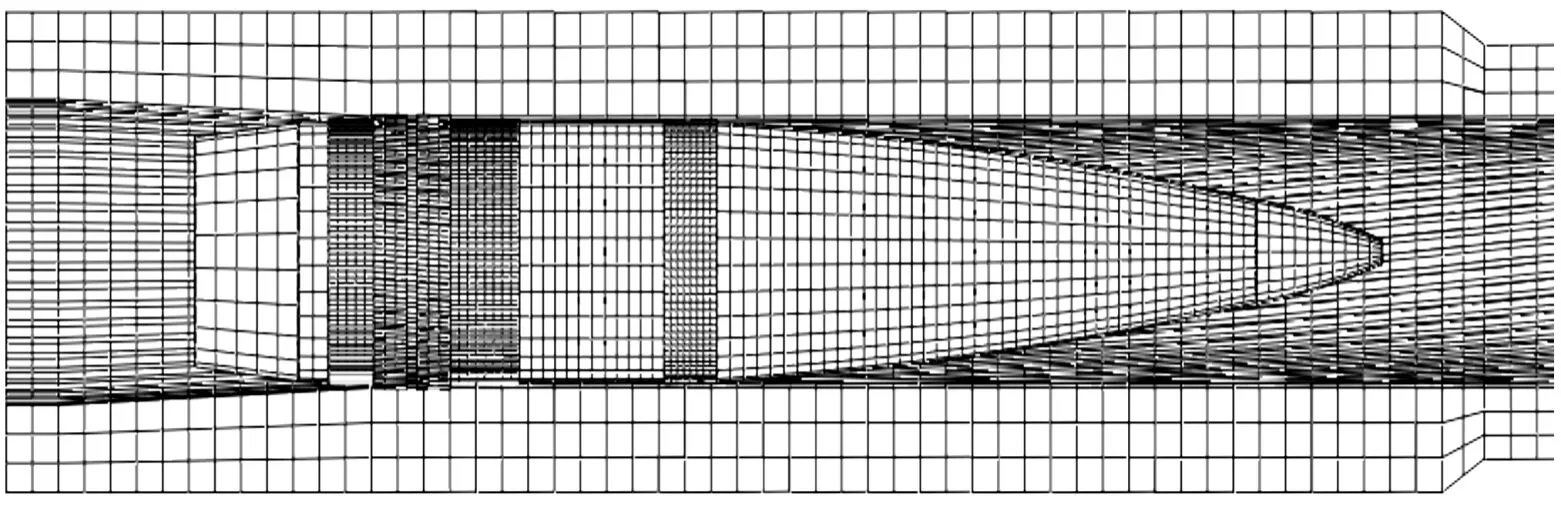
图2 弹炮耦合全炮动力学有限元模型

1.2 弹炮耦合参数化有限元模型

参数化建模是指在输入某些参数值后，实现对设计变量的动态更新，同时自动生成对应的全炮有限元模型，通过ABAQUS脚本接口(Abaqus Scripting Interface)，利用Python编程工具对全炮有限元模型的程序进行修改，实现弹炮耦合全炮动力学有限元的参数化[9]。

1.3 研究方案的设计与对比

本文研究轻型火炮回转部分质心位置的变化对弹丸起始扰动的影响时，作以下两点假设：

1) 仅考虑回转部分质心前后位置变化对弹丸起始扰动的影响，忽略回转部分质心在z方向和y方向位置微小改变的影响。

2) 忽略回转部分质心位置改变时，架体结构刚度的微小变化对弹丸起始扰动的影响。

基于以上假设，在参数化弹炮耦合动力学有限元模型中，以下架中心为回转轴原点，建立坐标系如下：与身管轴线重合的坐标轴为x轴，其正方向由炮尾指向炮口，与身管轴线垂直且指向上方为y轴正方向，z轴由右手定则确定。在参数化有限元模型中，回转部分质心位置无法直接控制，需要选择合适的结构参量间接控制质心位置。因此，根据参数化建模的原理和前人研究经验，选取总体结构参数设计变量：耳轴前后位置为a1，耳轴高为a2。此外，要实现火炮回转部分质心位置在z方向上变化，通过在有限元软件中，耦合质量点的方式调节集中点到身管轴端面的距离，即上架右侧质量点距回转轴距离为b1，上架左侧质量点距回转轴距离为b2。通过改变变量b1、b2可调节回转质心在z方向上的变化。

针对所要研究的问题，设计了如表1所示的轻型火炮回转部分质心位置对弹丸起始扰动影响的验证方案。在参数化弹炮耦合动力学有限元模型中，方案A0—A5通过参数化调整总体结构变量实现火炮回转部分质心在x轴方向变化对弹丸起始扰动的影响规律，其他两个方向质心位置不变。

表1 不同方案的质心位置

首先探索火炮回转部分质心在坐标轴各个方向的变化对弹丸起始扰动的影响规律。在参数化建模的基础上，通过调节总体结构参量变化实现火炮回转部分质心位置分别在坐标轴各个方向上的变化，有限元计算结果如图3～图6所示。其中回转角位移大小取绝对值，图5和图6中距离l指的是质心位置x。文中的回转角位移指弹丸水平方向角位移，俯仰角位移指弹丸竖直方向角位移。

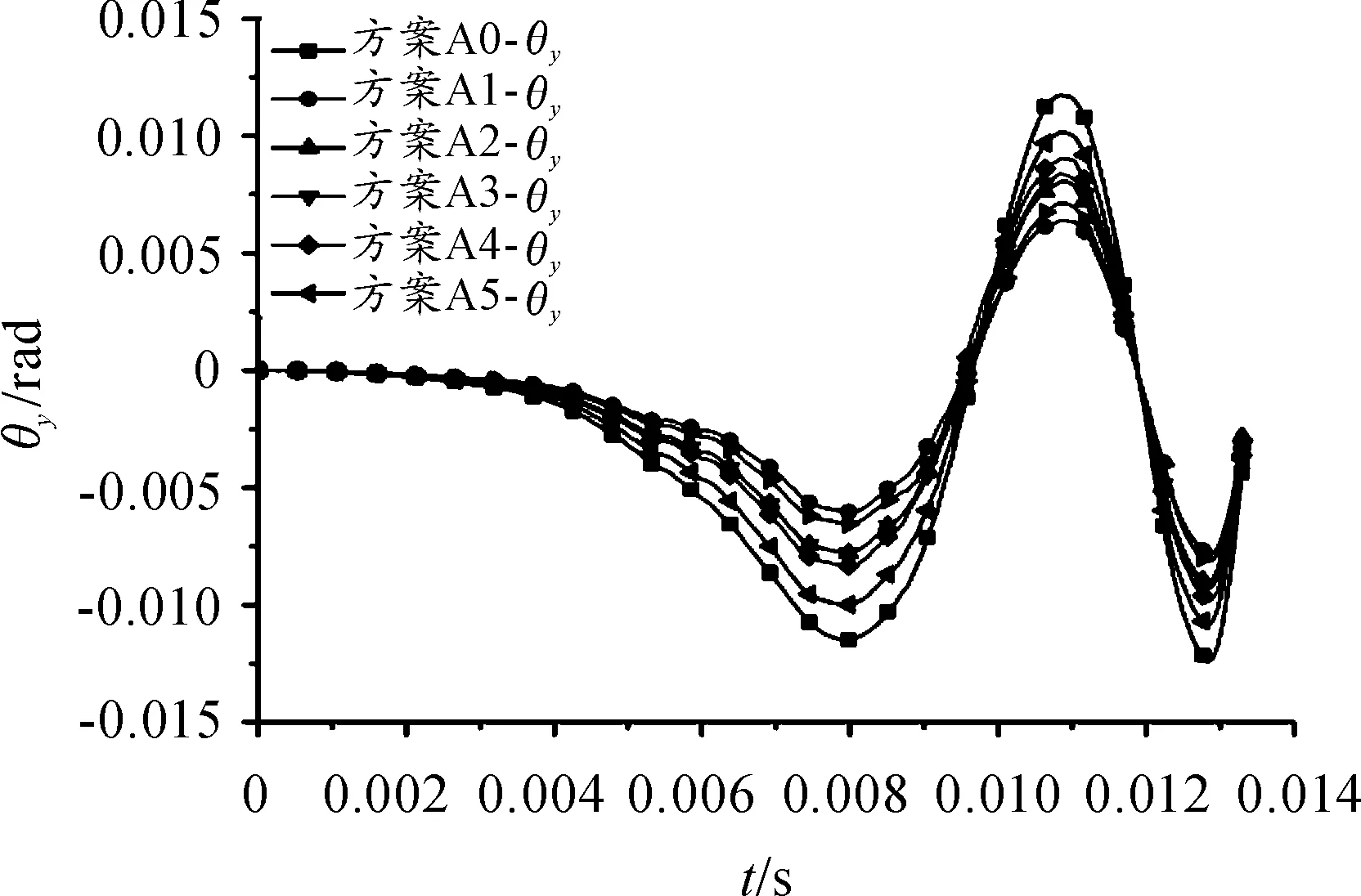
图3 弹丸回转角位移

图4 弹丸俯仰角位移

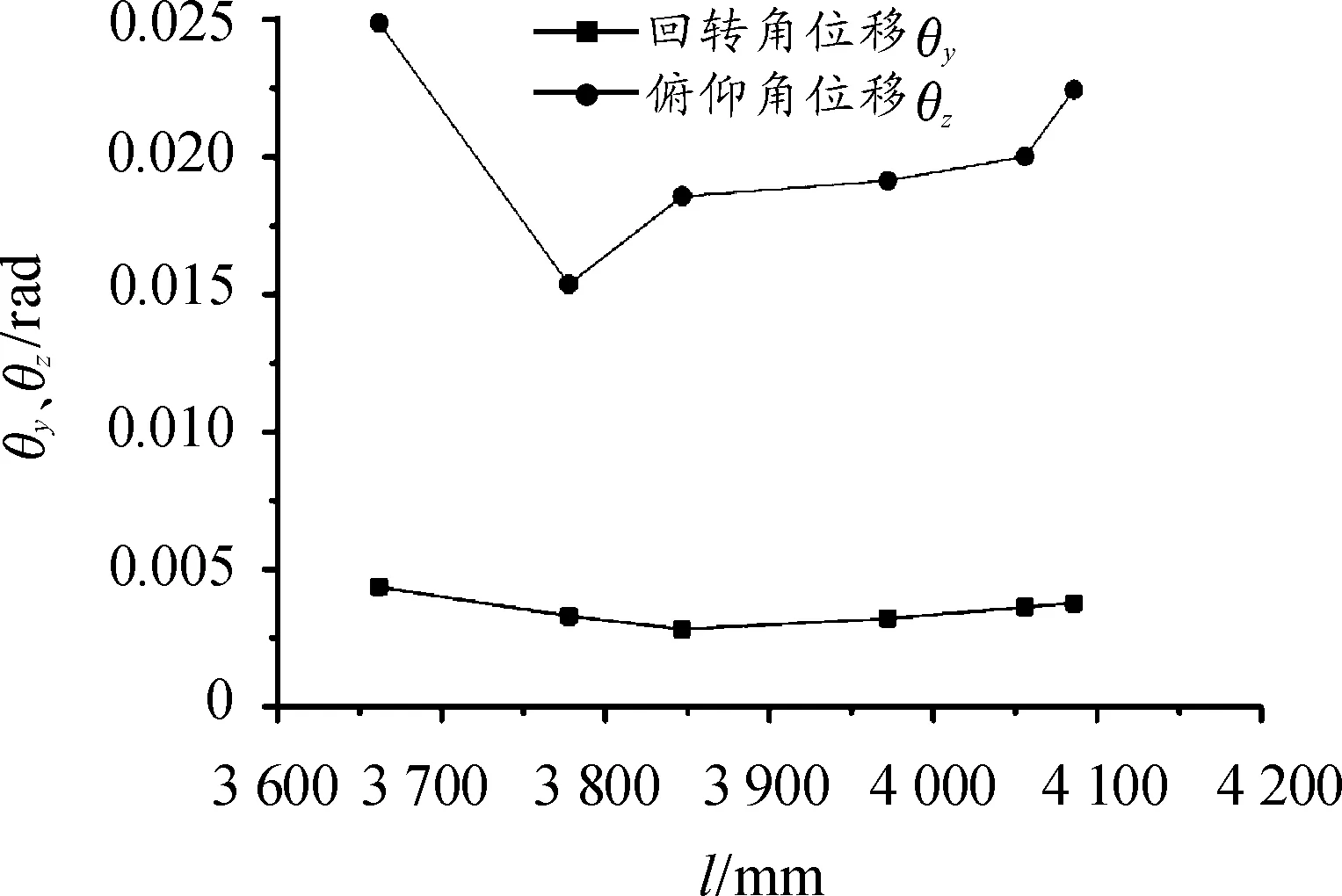
图5 弹丸角位移随距离l变化曲线

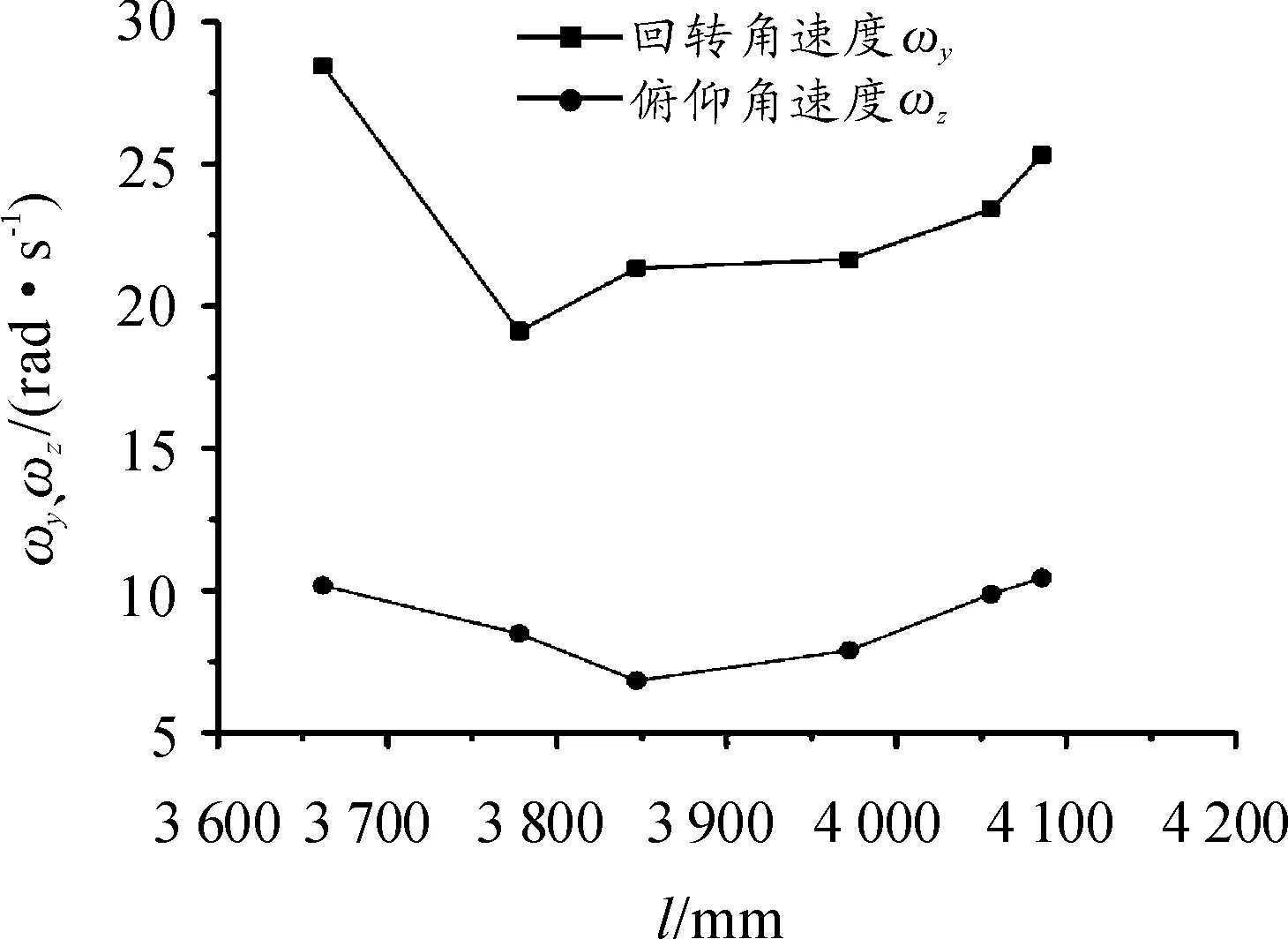
图6 弹丸角速度随距离l变化曲线

图3和图4分别描述了火炮回转部分质心位置在沿x轴方向变化时弹丸在膛内时期回转角位移和俯仰角位移随时间变化曲线，方案A0的回转角位移幅值曲线振幅最大，且出炮口时刻俯仰角位移最大。方案A1—A5的回转和俯仰角位移随距回转轴中心距离变大依次增加；图5和图6描述了弹丸出炮口时刻的角位移和角速度随质心距回转中心距离l的曲线变化关系，可以看出，火炮回转部分质心位置在沿身管轴线方向变化时，弹丸起始扰动呈现凹型变化规律，即质心位置远离回转中心，弹丸起始扰动影响较大，质心位置靠近回转轴中心，弹丸起始扰动也影响较大。弹丸发射期间，若回转部分质心距离回转轴中心较远时，架体支撑刚度不足，容易引起身管摆动，造成身管扰动较大；质心位置靠近回转轴中心时，发射过程中，身管摆动量变大，容易引起身管有向上摆动，从而弹丸起始扰动较大。

2 回转部分质心的优化

火炮是一个复杂的武器结构系统，回转部分结构布局作为直接影响射击精度的因素，其质心在没有优化前的随机位置如图7所示，前文研究结果表明，回转部分质心位置在沿身管轴线方向对弹丸起始扰动呈现凹型规律变化，且对弹丸起始扰动影响较为明显。影响火炮回转部分质心位置的方法有很多。本文通过调节影响火炮回转部分质心位置的总体结构变量来间接改变质心位置。在满足火炮射击稳定性的前提条件下，选取的结构优化设计变量为：耳轴中心距回转中心距离a1，耳轴高a2，上架右侧质量点距回转轴距离b1，上架左侧质量点距回转轴距离b2和火炮回转部分质量m。因此，在参数化建模基础上，将结构有限元技术与智能优化技术相结合，进而建立火炮回转部分质心变化对弹丸起始扰动的优化模型，研究在火炮弹丸初速度相同的前提下，影响火炮回转部分质心位置的总体结构参数的合理匹配。

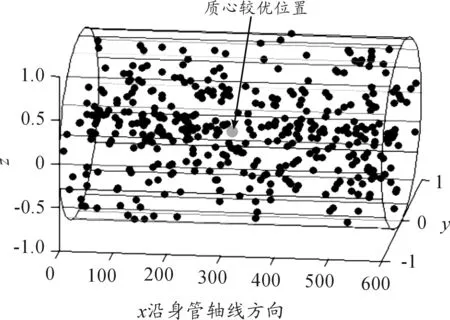
图7 火炮回转部分质心位置的随机分布示意图

2.1 近似模型的构建

近似模型方法是通过数学模型方法逼近一组输入变量和输出变量的方法，它是复杂优化设计问题中平衡计算代价和计算精度之间矛盾的常用方法和技术手段，其表达式如下：

y(x)=y1(x)+ε

(1)

式(1)中：y(x)为响应实际值；y1(x)为响应近似值；ε为近似值与实际值之间的随机误差。

考虑有限元模型计算中材料与接触的非线性，火炮回转部分结构参数与弹丸起始扰动之间存在着复杂的非线性映射关系[10]，不容易找到确定的函数关系。径向基函数是一类以待测点与样本点之间的欧式距离为自变量的函数，径向基函数可以很容易地把一个多维问题转化成以欧式距离为自变量的一维问题[3]。火炮总体结构较为复杂，其动态响应具有很强的非线性，所示训练样本数量必须足够充分。鉴于此，本文在Isight软件中采用最优拉丁超立方试验设计来安排试验[11]，共取280各个试验点，进行281次试验计算构建径向基神经网络近似模型。经过计算近似模型的近似误差，该近似模型的可信度较高。

2.2 目标函数的构建

根据前人的经验，本文拟用弹丸起始扰动来表征轻型火炮的射击精度，弹丸起始扰动由弹丸质心出炮口时刻的角位移、角速度与速度3个变量组成。为了便于研究，对弹丸起始扰动3个变量进行加权处理，构建针对弹丸起始扰动的目标函数[2]：

f = fVD+ fHD

(2)

其中：

式(2)中：fVD为纵向目标函数，fHD为横向目标函数，θZ、θy为弹丸质心的俯仰角位移和回转角位移，ωZ、ωy为弹丸质心的俯仰角速度和回转角速度；φZ、φy为弹丸质心的纵向速度和横向速度；θZ0、ωZ0、φZ0、θy0、ωZ0、φy0为相应的弹丸扰动参考值；α1、β1、γ1、α2、β2、γ2分别为各弹丸参量在归一化函数f中所占比值，且α1+β1+γ1+α2+β2+γ2=1。

结合式(2)和建立的径向基神经网络模型即可建立设计变量与目标函数之间的函数关系。

2.3 基于遗传算法的优化和结果分析

在获得火炮回转部分质心位置变化对弹丸起始扰动影响规律的基础上，本文尝试对质心位置进行优化，以目标函数f最小化为目标，各个设计变量的取值范围如表2所示。

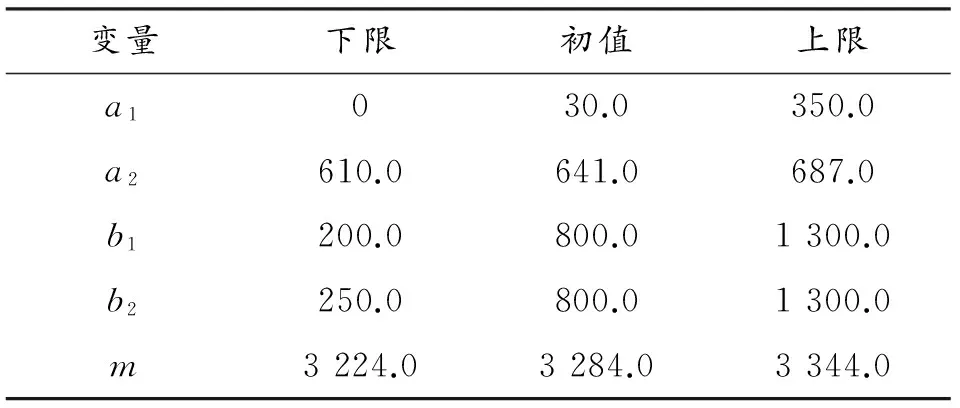
表2 优化设计变量的设计区间

在设计变量取值范围内采用遗传算法进行优化计算，经圆整后的结构参数优化结果如表3所示。

表3 优化后设计变量的值

优化后弹丸在膛内时期运动参量的对比曲线如图8～图10所示。

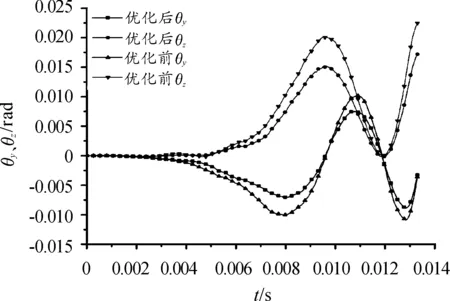
图8 弹丸角位移曲线

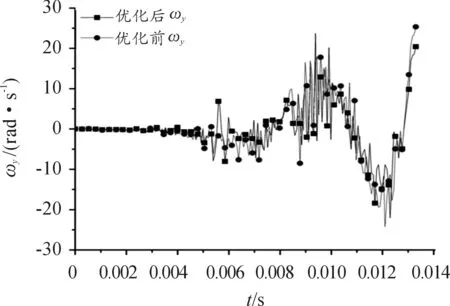
图9 弹丸回转角速度曲线

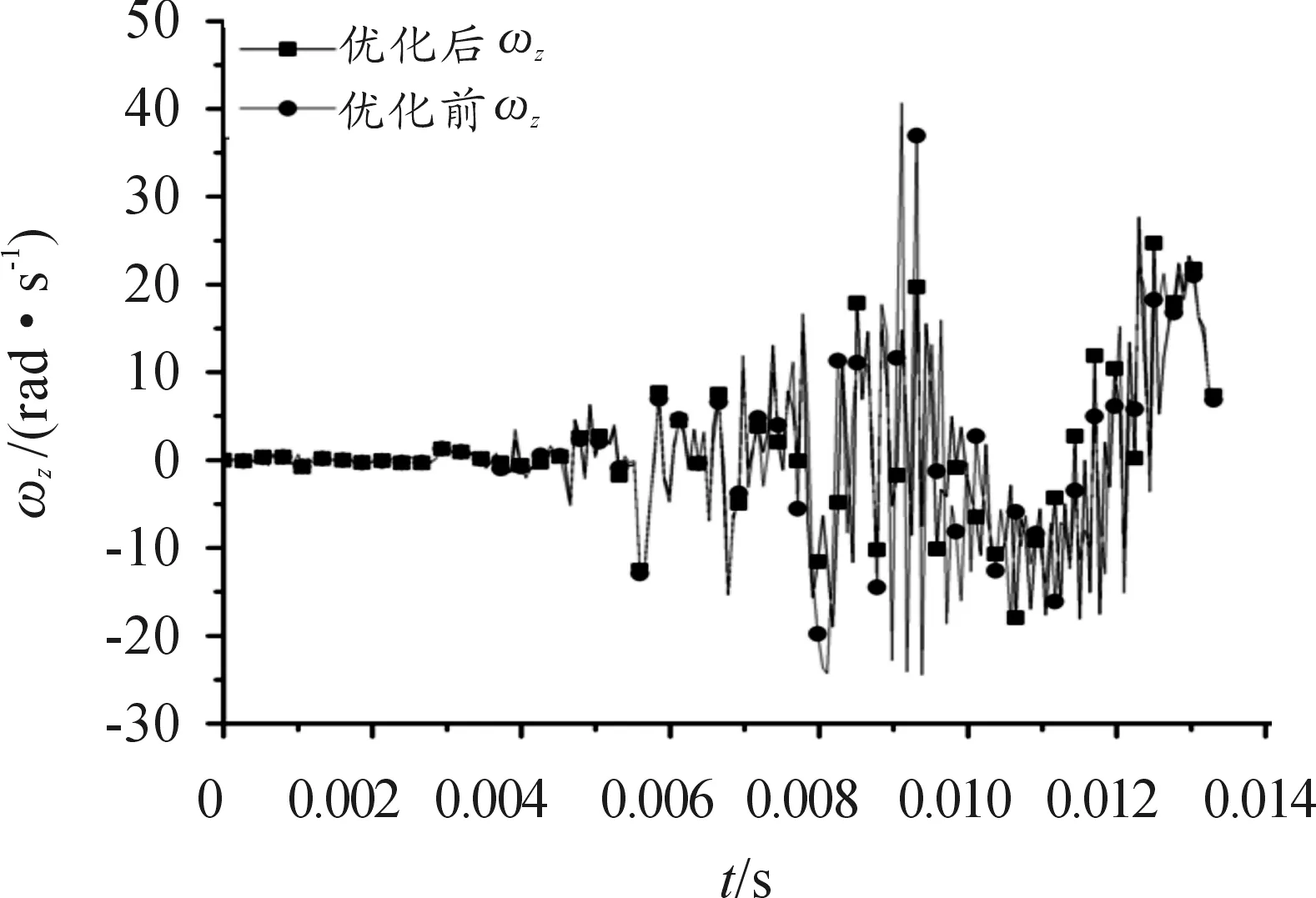
图10 弹丸俯仰角速度曲线

优化前回转部分质心位置和质量分别为(3 846.85, 651.45, 2.23)和3 284.94 kg，优化后的回转部分质心位置和质量分别为(3 779.32, 617.85, -1.49)和3 262.23 kg。

由图8～图10优化结果对比可知，优化后弹丸出炮口时刻俯仰角位移相对于优化前有明显减小，弹丸出炮口时刻的回转角速度相对于优化前有一定的降低；回转角位移和俯仰的角速度在出炮口时刻几乎不变，但是在膛内时期的振幅相对于优化前有所降低。总体表明：经优化后的火炮回转部分质量质心对弹丸起始扰动影响减小。

3 结论

火炮不同方案的回转部分质心位置沿身管轴线方向变化对弹丸起始扰动有一定的影响，随着距回转轴中心距离的变化，弹丸出炮口时刻的角位移和角速度呈现凹型变化规律，回转部分质心位置的设计存在一个较为合理范围，使弹丸起始扰动影响相对较小。研究结果对提高大口径轻型火炮的射击精度具有一定的参考价值。

在满足射击稳定性的前提下，通过对影响某轻型火炮回转部分质心位置的结构参量的优化匹配，获得了回转部分较优的质心位置，优化后的弹丸出炮口时刻的角位移和角速度、弹丸在膛内时期的振动幅度较优化前均有减小。该优化方法取得了较为满意的结果，对火炮工程设计具有应用价值。

[1] 张相炎.火炮设计理论[M].北京：北京理工大学出版社，2004.

[2] 李强,顾克秋.影响弹丸起始扰动的火炮结构参数灵敏度分析与优化研究[J].火炮发射与控制,2014,36(4)：39-43.

[3] 梁传建,杨国来.基于神经网络和遗传算法的火炮结构动力学优化[J].兵工学报，2015,36(5)789-794.

[4] 崔凯波，秦俊奇，贾长治.炮口扰动影响参数分析与优化研究[J].火炮发射与控制学报，2010(3):34-.37.

[5] 葛建立,杨国来,曾晋春.某自行火炮结构参数灵敏度分析与优化[J].火炮发射与控制学报,2007(1):16-19.

[6] 张俊飞,顾克秋,付帅.基于有限元弹炮耦合的某牵引火炮炮口扰动灵敏度分析[J].火炮发射与控制学报,2014，35(1):25-30.

[7] 彭迪.超轻型火炮结构动力学有限元分析与总体优化匹配技术研究[D].南京:南京理工大学,2011.

[8] 林秉奇.基于弹炮耦合的火炮非线性动态特性分析与研究[D].南京：南京理工大学.2013.

[9] 楚志远，杨国来，陈运生.自行火炮有限元参数化建模方法[J].南京理工大学学报，2002,26(2)：120-122.

[10]曹宁.车载炮射击精度分析[D].南京：南京理工大学，2012.

[11]赖宇阳.Isight参数化理论与实例详解[M].北京：北京航空航天大学出版社，2012

[12]毛保全，胡涛，吴永亮，等.射速对顶置武器站连发精度的影响[J].兵工自动化，2014(10):56-59.

(责任编辑周江川)

Study and Optimization of the Influence of the Initial Projectile Disturbances Caused by the Change Position of the Howitzer Revolution’s Centroid

ZOU Li-bo, GU Ke-qiu

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

In order to improve the fire accuracy of the ultra towed howitzer, the author studied the influence of initial projectile disturbances caused by the change position of the howitzer revolution’s centroid which is controlled by adjusting the whole structural parameters that effects the position of the howitzer revolution’s centroid. On this base, the author built a parametric and dynamic finite element model about relationship between the change position of the howitzer revolution’s centroid and initial projectile disturbances. The result reveals the change position of the howitzer revolution’s centroid has an influence on the initial projectile disturbances. Otherwise, based on this rule that the rules of initial projectile disturbances due to the change position of the howitzer revolution’s centroid, the author optimized the position of the howitzer revolution’s centroid with the genetic algorithm. The results can provide theoretical guide for the whole structure design of the ultra towed howitzer.

centroid of the howitzer revolution; initial projectile disturbances; light gun; optimization

2016-07-27；

邹利波(1990—)，男，硕士，主要从事装备理论与装备技术研究。

10.11809/scbgxb2016.12.013

邹利波，顾克秋.火炮回转质心对弹丸起始扰动的影响研究与优化[J].兵器装备工程学报，2016(12):51-55.

format:ZOU Li-bo, GU Ke-qiu.Study and Optimization of the Influence of the Initial Projectile Disturbances Caused by the Change Position of the Howitzer Revolution’s Centroid [J].Journal of Ordnance Equipment Engineering,2016(12):51-55.

TJ33

A

2096-2304(2016)12-0051-05

修回日期：2016-09-30