旭日型磁控管谐振系统的等效电路模型与分析

曹振平

(江苏联合职业技术学院 苏州分院， 江苏 苏州 215009)

·收/发技术·

旭日型磁控管谐振系统的等效电路模型与分析

曹振平

(江苏联合职业技术学院 苏州分院， 江苏 苏州 215009)

通过分析旭日型磁控管的等效电路，利用扇形谐振腔的等效电容和等效电感的计算公式，计算旭日型磁控管各模式的谐振频率；简化了谐振频率的计算公式，得到了谐振频率关于结构尺寸的解析表达式；分析了π模谐振频率随大、小腔的半径、角度的变化情况。结果表明：等效电路计算结果与仿真结果基本一致，特别是π模谐振频率十分相符。因此，该等效电路计算方法是可行的。π模谐振频率随大、小腔半径和小腔角度的增大而减小，随大腔角度的增大而增大，研究结果有助于旭日型磁控管的预先设计与分析。

旭日型磁控管；等效电路；模谱图；π模谐振频率

0 引 言

磁控管是一种大功率、高效率、低成本的微波源，广泛应用于军民领域。为使磁控管稳定工作，需要增大模式分隔度。对于波长大于3 cm的磁控管，通常采用隔模带来增大模式分隔度；对于波长小于3 cm的磁控管，则采用旭日型谐振系统，便于加工，同时降低了高频损耗，提高谐振腔的品质因数。此外，对于阳极块高度较大的长波长磁控管，隔模带效果不理想，可采用旭日型谐振系统。

旭日型谐振系统是一种异腔结构，由大小两组尺寸不同的谐振腔交替排列而成，大谐振腔的谐振频率较低，小谐振腔的谐振频率较高。从慢波结构的角度分析，旭日型谐振系统属于一种双阶系统，其色散特性曲线分成两组，即有两个通带，一组频率较高，另一组

频率较低[1-2]。

求解磁控管的π模谐振频率的方法主要有四种：场分析、计算机仿真、实验冷测和等效电路法。其中，场分析法需要求解超越方程，且无法给出谐振频率关于结构尺寸的表达式[3-6]；计算机仿真需要较长时间[7-8]；实验冷测则需要加工出完整的磁控管，成本过高，不适于磁控管的预先分析与设计[9-10]；等效电路法通过电容、电感与结构的对应关系，求解出谐振腔的电容与电感，再通过磁控管等效电路得出谐振频率的计算公式，进而得出谐振频率关于结构尺寸的解析表达式[11]。

1 旭日型磁控管等效电路

1.1 等效电路模型

以常用的18腔旭日型磁控管为例，其横截面如图1所示。

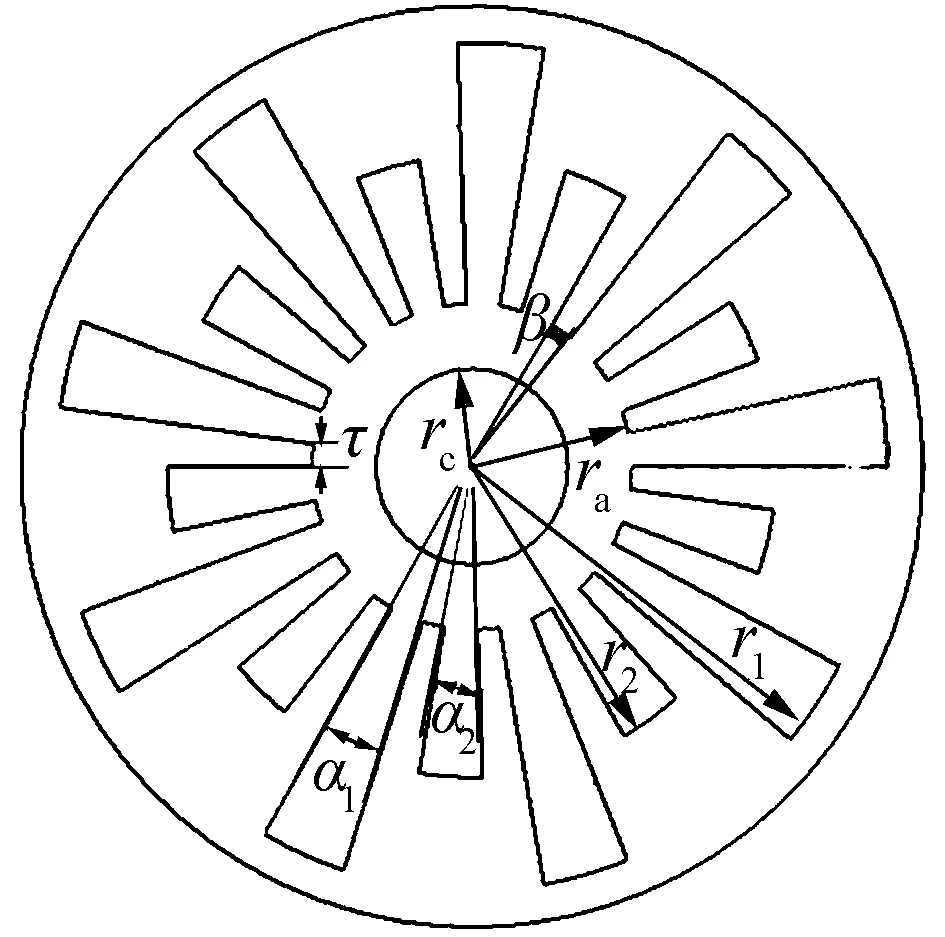
图1 旭日型磁控管的横截面

图1中，rc、ra、r1、r2分别为阴极、阳极、大腔、小腔的半径，大、小扇形腔的角度分别为α1和α2，对于N腔旭日型磁控管，侧壁角度为β=2π/N-α1/2-α2/2，厚度为τ=βra，谐振腔可以等效成电容C和电感L的并联电路，对于磁控管谐振腔，还存在各腔之间的耦合电容，也就是阴阳极电容Ck，单个谐振腔的等效电路如图2所示。

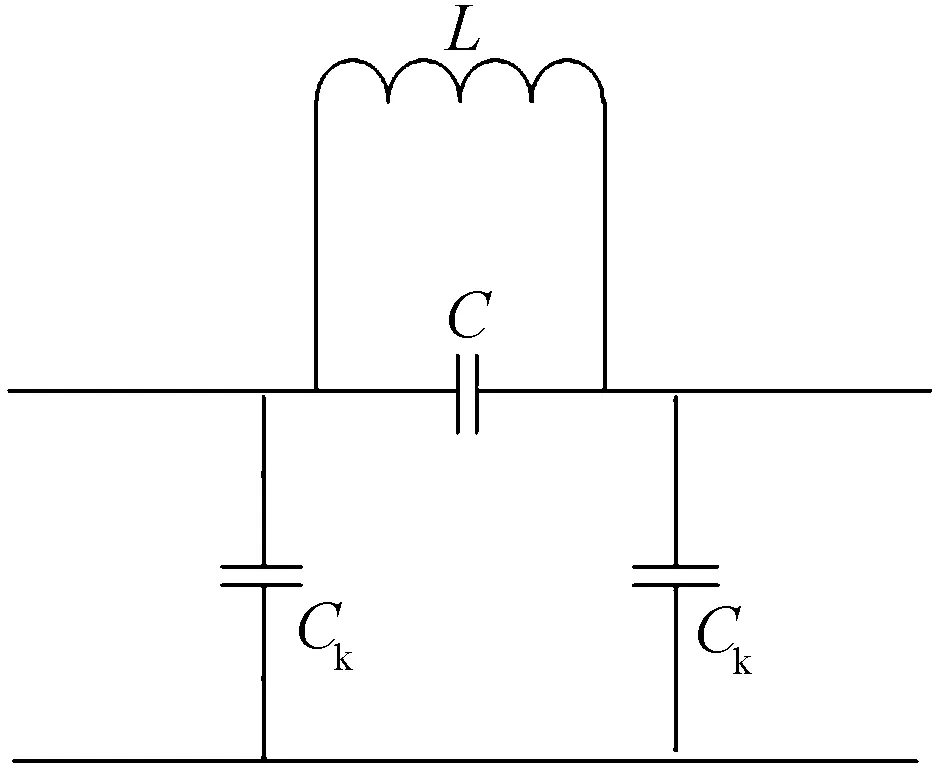
图2 单个磁控管谐振腔等效电路

N腔磁控管的等效电路就是由N个图2中等效电路首尾相接构成的。对于旭日型磁控管，由于相邻谐振腔的大小不同，从而谐振腔等效电容和等效电感也不相同，其部分等效电路如图3所示[16]。

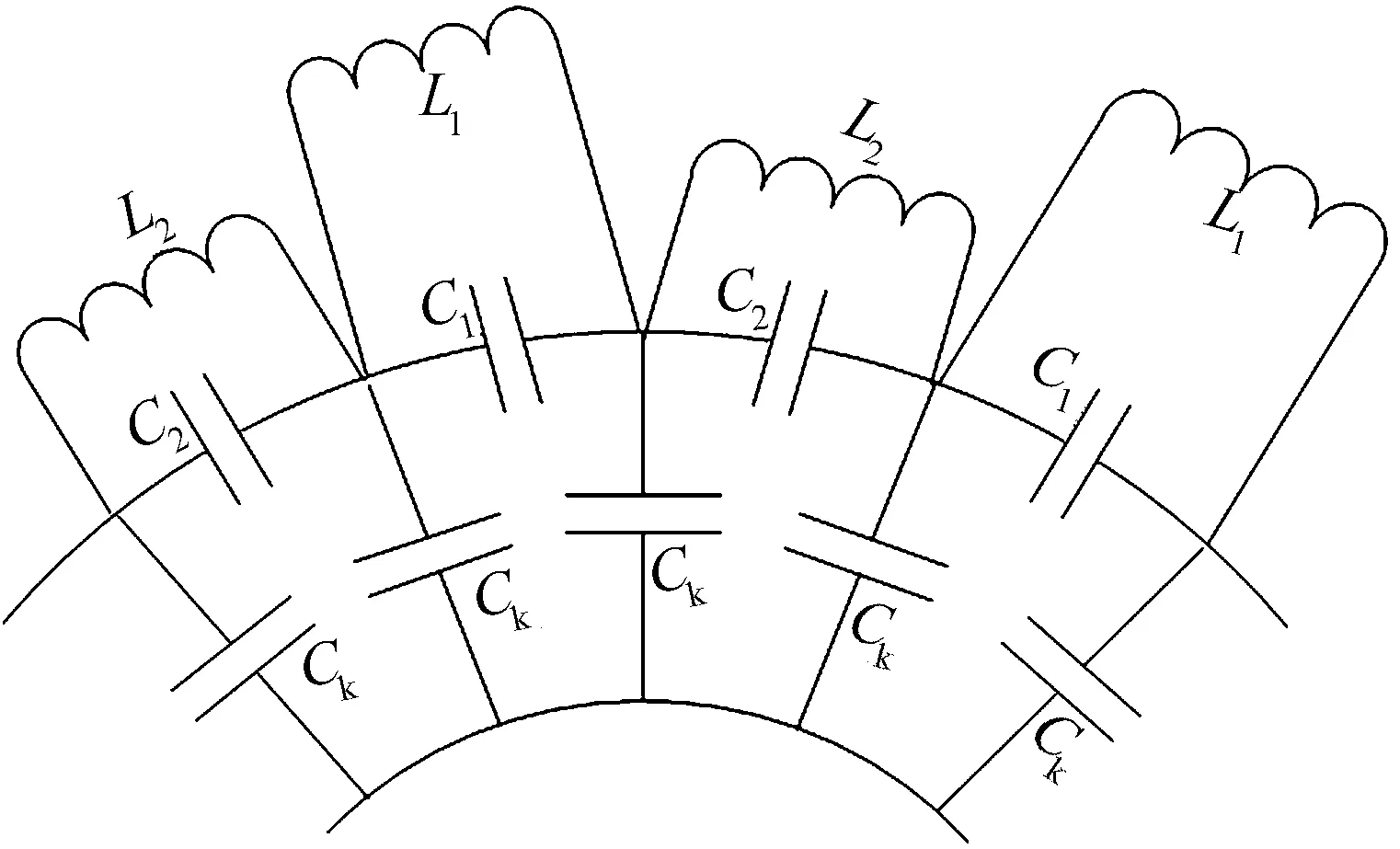
图3 旭日型磁控管谐振腔的部分等效电路

图3中，L1、C1分别为大谐振腔的等效电感和等效电容，L2、C2分别为小谐振腔的等效电感和等效电容。

1.2 等效电路求解

对于N个同腔的磁控管，各模式的谐振频率表达式为[1]

(1)

从而有

(2)

对于N腔旭日型磁控管，其频谱特性会分裂成两条曲线，即大、小谐振腔的频谱曲线。对于大谐振腔，有

(3)

小谐振腔，有

(4)

若要计算整个旭日型磁控管的谐振频率，则要综合考虑大小腔谐振系统及其耦合，根据霍尔电压及电流定律，可得旭日型磁控管谐振频率的表达式为[16]

cosΦ=2cosφ1cosφ2-1

(5)

将式(3)、式(4)代入式(5)可得

(6)

式中：ω1,0、ω2,0分别为大小谐振腔的谐振频率；Φ=4πn/N，n=1,2,…,N/2。

通过求解式(6)，即可得到各模式的谐振频率。但是，式(6)不是模式频率的显式表达式，需要借助Matlab等计算工具才能方便求解，不便于分析计算。因此，需要对式(6)进行简化处理。

通过对旭日型磁控管谐振系统分析可知[1]：(1)如果谐振系统激励起的振荡在较低频率范围之内，接近于单个大腔的谐振频率，从相互作用空间来看，可以近似地认为小腔并不存在。这时，在大腔口处的高频电场较强，而在小腔口处的高频电场很弱，耦合主要存在于大腔之间。(2)当激励起的振荡在接近于小腔谐振频率的范围内时，可以近似地认为大腔并不存在。此时，在大腔口处的高频电场较弱，而在小腔口处的高频电场较强，耦合主要存在于小腔之间。(3)如果激励起的振荡频率范围落在大腔与小腔的谐振频率之间时，大腔与小腔将同时起作用。这时，在大、小腔口处的高频电场强度相差不大，是大、小腔间耦合最强的状态，此时磁控管工作在π模。

频率较低的模式，以大腔的振荡为主，因此，可以忽略小腔的振荡，采用式(3)计算低次模的谐振频率；同理，频率较高的模式，以小腔的振荡为主，因此，可以忽略大腔的振荡，采用式(4)计算高次模的谐振频率。通常，耦合电容Ck相对于谐振腔电容C1、C2比较小，此时式(6)最后一项可以忽略，从而可以得到简化的π模频率表达式[13]

(7)

采用这种近似的处理方式仅限于一般的旭日型磁控管，若大小腔尺寸相近，则相互之间的耦合较强，使得近似处理的条件不再成立，但式(6)是通过电路分析得到的，其依然成立。当大小腔半径相同时，即为同形腔的情形。此时，式(6)可以写成

(8)

由于Φ=4πn/N，φ=2πn/N，Φ=2φ，cosΦ=cos(2φ)=2cos2φ-1，从而有

(9)

因此，式(6)的适用范围比式(7)及其简化方法更加广泛。对于一般旭日型磁控管，该近似方法的可行性将在下一节进行证明。

采用扇形腔等效电感、电容的计算公式[15]，可得大腔等效电感、等效电容分别为

(10)

(11)

式中：D1=r1-ra，为大腔的深度。

小腔的等效电感、等效电容分别为

(12)

(13)

式中：与大腔类似，D2=r2-ra，为小腔的深度。

耦合电容表达式为

(14)

将式(10)～式(14)代入式(6)，即可求得旭日型磁控管各模式的谐振频率。将式(10)～式(14)代入式(3)、式(4)、式(7)，即可通过简化求解得到旭日型磁控管各模式的谐振频率。其中，π模的谐振频率表达式为

(15)

其中

2 等效电路的仿真验证

以18腔旭日型磁控管为例，其各个结构尺寸分别为rc=1.22 mm，ra=2.03 mm，r1=4.95 mm，r2=3.68 mm，h=4.83 mm，α1=α2=12°。利用上一节的理论进行计算，采用CST软件建立对应的仿真模型，计算各模式的谐振频率。理论计算结果和仿真结果如表1所示。

表1 18腔旭日型磁控管各模式谐振频率

表1中，相对误差1为两种计算方法得到的结果之间的相对误差，采用|式(6)-简化|/简化×100%；相对误差2为式(6)计算结果与仿真结果之间的相对误差，采用|式(6)-仿真|/式(6)×100%。

为了更加直观地表示，将上述结果用图形的方式进行表述，三种方法得到的模谱如图4所示。

图4 18腔旭日型磁控管模谱图

其他尺寸不变，将其改为20腔，理论计算结果和仿真结果如表2所示。

表2 20腔旭日型磁控管各模式谐振频率

相对误差1、2的计算方法与表1相同。

采用上述方法绘制其模谱图，如图5所示。

图5 20腔旭日型磁控管模谱图

从表1、表2、图4、图5中可以看出，式(6)以及简化后的等效电路计算结果与仿真结果基本吻合，最大误差出现在大腔的最低次模，也就是整个磁控管的最低次模，该结果与文献[15]中的类似。主要原因是大腔的最低次模远离π模，其电流分布与计算等效电感时所设定的电流分布有差别。但对于对工作性能有较大影响的大、小腔的高次模，特别是π模，理论计算结果与仿真结果十分相符，因此该等效电路理论对于分析π模及大、小腔的高次模是准确可行的。同时可以看到，采用完整的理论式(6)计算得到的结果与简化后的理论计算结果基本相符。因此，对于一般的旭日型磁控管，可以采用简化后的理论对其谐振频率进行计算分析，但对于大小腔尺寸较为接近的旭日型磁控管，由于其邻近腔之间的耦合较为强烈，需要采用完整的理论式(6)计算其谐振频率。

3 π模谐振频率影响因素分析

等效电路优势在于能够得到谐振频率关于结构尺寸的解析表达式，从而便于分析各结构尺寸对谐振频率的影响。在上一节的分析中，π模简化理论计算结果与仿真结果非常吻合。与同腔磁控管相比，旭日型磁控管阴、阳极半径对谐振频率的影响相似，其特殊的影响因素是大、小腔的结构尺寸。因此，在阴、阳极半径固定的条件下，利用式(15)分析大小腔的结构尺寸对π模谐振频率的影响，由于式(15)的局限性，各结构尺寸取值时不能过于极端，因此，我们在上节采用的磁控管基础上进行结构调整。

采用18腔旭日型磁控管模型，rc=1.22 mm，ra=2.03 mm，h=4.83 mm。按以下四种情形分析大小腔的半径、角度对π模谐振频率的影响。

情形1：r2=3.68 mm，α1=α2=12°，观察大腔半径r1对π模谐振频率的影响；

情形2：r1=4.95 mm，α1=α2=12°，观察小腔半径r2对π模谐振频率的影响；

情形3：r1=4.95 mm，r2=3.68 mm，α2=12°，观察大腔角度α1对π模谐振频率的影响；

情形4：r1=4.95 mm，r2=3.68 mm，α1=12°，观察小腔角度α2对π模谐振频率的影响。

将四种情形的结构尺寸代入式(15)进行计算，得到π模谐振频率随大腔半径、小腔半径、大腔角度、小腔角度的变化分别如图6a)～图6d)所示。

图6 π模谐振频率随结构尺寸的变化

从图6中可以看出，π模谐振频率随大腔半径r1、小腔半径r2和小腔角度α2的增大而减小，随大腔角度α1的增大而增大，该结论与文献[5]的场分析结论相符。因此，若要增大π模谐振频率，可以在适当范围内减小大腔半径r1、小腔半径r2和小腔角度α2，增大大腔角度α1。

从式(15)可以看出，π模谐振频率与高度无关，这与实际情况是不相符的，其原因是等效电路理论没有考虑临近腔体之间的电感耦合。当腔体高度较小时，这种耦合会对谐振频率产生较大的影响，但对于一般磁控管，特别是旭日型磁控管，其腔体高度通常较大，这种耦合的影响非常小。因此，本文的理论结果是适用的。

4 结束语

本文从旭日型磁控管谐振腔的等效电路出发，将同腔磁控管的等效电路理论应用到旭日型磁控管，得到了旭日型磁控管谐振系统的等效电路模型。通过对旭日型磁控管谐振特性进行分析，简化了该等效电路方法，得到了旭日型磁控管谐振频率关于结构尺寸的解析表达式。采用CST-MWS软件建立了旭日型磁控管仿真模型并得到了各模式的谐振频率，将仿真结果与等效电路计算结果进行对比。对旭日型磁控管π模谐振频率解析表达式进行数值计算，分析了大小腔的半径、角度对π模谐振频率的影响。结果表明：各模式谐振频率的等效电路计算结果与仿真结果相符，特别是π模谐振频率。π模谐振频率随大腔半径r1、小腔半径r2和小腔角度α2的增大而减小，随大腔角度α1的增大而增大。本文的研究结果有助于旭日型磁控管的预先设计与分析。

[1] 张兆镗. 微波电子管原理[M]. 北京: 国防工业出版社, 1981. ZHANG Zhaotang. Principle of microwave tube[M]. Bejing: National Denfense Industry Press, 1981.

[2] 电子管设计手册编辑委员会. 磁控管设计手册[M]. 北京: 国防工业出版社, 1979. Editorial Committce of Electronic Tube Design Handbook. Magnetron design handbook[M]. Bejing: National Defense Industry Press, 1979.

[3] 李 伟, 刘永贵. 类磁控管结构的理论分析[J]. 物理学报, 2012, 61(2): 021103-1-021103-5. LI Wei, LIU Yonggui. Theoretical analysis of magnetronlike structure[J]. Acta Physica Sinica, 2012, 61(2): 021103-1-021103-5.

[4] COLLINS G B. Microwave magnetrons[M]. New York: McGraw-Hill, 1948.

[5] 史迪夫, 王弘刚, 李 伟, 等. 扇形腔旭日型磁控管结构的理论分析与数字模拟[J]. 物理学报, 2013, 62(15): 151101-1-151101-7. SHI Difu, WANG Honggang, LI Wei, et al. Theoretical analysis and numerical simulation of rising sun magnetion with sector cavities[J]. Acta Physica Sinica, 2013, 62(15): 151101-1-151101-7.

[6] KROLL N M, LAMBRJR W E. The resonant modes of the rising sun and other unstrapped magnetron anode blocks[J]. Journal of Applied Physics, 1948,19(2): 166-187.

[7] BALK M C. 3D magnetron simulation by means of graphical processing units with CST studio suite[C]// IEEE Thirteenth International Vacuum Electronics Conference (IVEC). Monterey: IEEE Press, 2012: 25-26.

[8] 丁 帅，贾宝富，李飞雪. 一种5.8 GHz磁控管谐振系统的模拟分析[J]. 真空电子技术, 2008(6): 30-33. DING Shuai, JIA Baofu, LI Feixue. Simulation analysis of 5.8 GHz magnetron resonance system[J]. Vacuum Electronics, 2007(6): 30-33.

[9] IMRAN T, AD and CARTER R. Noise performance of frequency and phase-locked CW magnetrons operated as current-controlled oscillators[J]. IEEE Transactions on Electron Devices, 2005, 52(9): 2096-2103.

[10] 郭天鹏, 曾正华, 郭庆功, 等. C波段高稳定度磁控管微波源实验研究[J]. 电子信息对抗技术, 2012, 27(3): 74-77. GUO Tianpeng, ZENG Zhenghua, GUO Qinggong, et al. Experimental study on C band magnetron microwave sources with high stabilization[J]. Electronic Information Warfare Technology, 2012, 27(3): 74-77.

[11] 萨姆索诺夫. 多腔磁控管的计算和设计原理[M]. 北京: 国防工业出版社, 1975. SUMSOROV A E. The calculation and design theory of multicality magnetron[M]. Beijing: National Defense Industry Press, 1975.

曹振平 男，1963年生，本科，副教授。研究方向为电子技术、通信技术、探测技术等。

Equivalent Circuit Model and Analysis of Rising-sun Magnetron Resonant System

CAO Zhenping

(Suzhou Branch of Jiangsu Union Technical Institute, Suzhou 215009, China)

Equivalent circuit of rising-sun magnetron is analyzed in this paper, and resonant frequencies of each mode are calculated by expressions of equivalent capacitance and inductance of sector cavity. The formula of resonant frequency was simplified and then an expression of resonant frequency as a function of structure dimensions is derived. Moreover, the influence of structure dimensions on π-mode resonant frequency is analyzed. The results showed that the equivalent circuit result is consistent with simulation result, approximately. Especially, the π-mode resonant frequencies obtained by two methods are consistent well with each other. Besides, π-moderesonant frequency increased with the increasing of big cavity radius, small cavity radius and its angle, while it increases with the decreasing of small cavity angle. Therefore, the equivalent circuit theory in this paper is available and it can help to predesign and analyze resonant system of rising-sun magnetron.

rising-sun magnetron; equivalent circuit; mode spectrum; π-mode resonant frequency

10.16592/ j.cnki.1004-7859.2016.12.015

曹振平 Email：2843899056@qq.com

2016-09-17

2016-11-19

TN957

A

1004-7859(2016)12-0073-05