线阵干涉仪与均匀线阵DBF测向性能对比

夏鸿宝，周国永，左登朝，吴上游，舒 汀

(1. 南京科瑞达电子装备有限责任公司， 南京 211100) (2. 上海交通大学 上海市智能探测与识别重点实验室， 上海 200240)

·DBF在现代雷达中的应用·

线阵干涉仪与均匀线阵DBF测向性能对比

夏鸿宝1，周国永1，左登朝1，吴上游1，舒 汀2

(1. 南京科瑞达电子装备有限责任公司， 南京 211100) (2. 上海交通大学 上海市智能探测与识别重点实验室， 上海 200240)

从干涉仪线阵测向系统和均匀线阵DBF测向系统的组成和工作原理入手，介绍了两种测向系统的处理流程，推导了方位估计的C-R下界，通过对C-R下界的分析，对比了两种测向系统的性能，并根据两系统的工作特点，分析其应用场景。所得结论对工程人员具有重要的参考价值。

数字干涉仪测向; DBF测向; C-R下界

0 引 言

在雷达和电子对抗领域，目标的方位可以表征目标的空间信息，是一项基本测量参数[1]。方位测量结果可用于目标的无源定位、多感器信息融合、干扰机角度引导、反辐射攻击引导等。方位测量精度是电子侦察接收机性能的重要表征参数，通常作为系统的核心指标之一。

常用的测向方法有时差法、波束搜索法、多波束测向、数字波束形成(DBF)测向、干涉仪测向和空间谱估计算法等[2]。相位干涉仪具有设备量小、处理时间短和测向精度高的优点，尤其适用于机载平台，得到广泛使用。DBF由于具备灵敏度高、处理灵活以及宽角度覆盖的特点，一直广受关注，然而，受制于体积、重量和功耗以及有限的瞬时带宽，在机载平台难以推广。随着电子技术的快速发展，微波电路和数字电路小型化程度普遍提升，DBF技术的体积重量和功耗大幅下降，瞬时带宽大幅提升，初步满足在机载平台应用需求，目前正逐步走向实用。

本文从理论角度分析两种测向体制的方位测量误差，分析二者之间的性能特点，为后续电子对抗装备的技术体制选择提供依据。

1 干涉仪测向原理及系统组成

设M元天线组成的直线干涉仪阵列，如图 1所示，该阵列可以选择M条基线，基线长度分别为d1,，d2，…，dM。干涉仪测向精度仅与最长基线长度相关，假设一个中心频率为f的窄带信号入射，则第一个阵元和最后一个阵元的接收信号分别为

s1(t)=Acos(2πft+φ0)+n1(t)

(1)

(2)

式中：n1(t)和nM(t)分别为观测噪声，通常满足高斯白噪声假设；φ0为信号初始相位，相位未知，通常满足[0,2π)均匀分布。

图1 M阵元干涉仪布阵示意

数字式干涉仪测向设备处理流程如图 2所示，将天线接收的射频信号放大变频至中频频率，数字接收机采集各路天线的中频信号并进行信道化处理，对其中一路天线的信道化输出进行检测，测量该路的脉冲参数如频率、脉宽以及幅度等信息，根据检测的结果提取各个天线通道的相位信息，利用相位信息解算方位模糊并计算最终的信号方位角，解模糊的方法可以有很多种，与布阵的形式有关，具体可参见文献[3-5]，这里就不再详细描述。

图2 干涉仪处理流程示意

干涉仪的最终测向精度取决于最长基线的长度，经过解模糊后，可以得到方位的估计值为

(3)

式中：ΔφM=φM-φ1为测量的模糊相位；k为模糊倍数需要通过相位解模糊得到。

2 均匀线阵DBF测向原理及系统组成

设N元天线组成的均匀直线阵列，阵元间距为d，如图3所示，对于假设一个中心频率为f的窄带信号入射，则第i个阵元接收信号为

(4)

式中：ni(t)为观测噪声，通常假设为高斯白噪声；φ0为信号初始相位，相位未知，服从[0,2π]均匀分布。

图3 N阵元均匀线阵布阵示意

数字波束形成DBF接收机的处理流程如图4所示，与数字干涉仪一样，将接收的射频信号转换到中频，对中频信号进行模数变换采集，对采集到的信号进行DBF处理，输出信号再进行信道化处理，检测并测量脉冲参数。DBF测向具体方法可以参见文献[6-8]，这里为了后续便于推导准确的误差分布，不直接采用比幅直接测向方法，而使用间接测量的方法，估计估计得到的信号空间频率为F，根据空间频率估计信号的方位。

(5)

式中：λ为信号波长；d为阵元间距；F为空间频率。

图4 DBF处理流程示意

3 干涉仪测向误差

干涉仪测向的首先要估计通道之间的相位差，而相位估计通常都是非线性的，信号的相位估计值为

(6)

式中：SI，SQ分别为信号解调后的同相和正交分量。

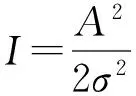
(7)

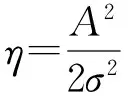
图5 相位测量的均方误差统计

图6 相位测量的误差概率分布统计

图7 相位测量均方根误差统计

观察可以发现，在输入信噪比小于15 dB条件下，相位检测均方误差大于信噪比倒数。这是由于当信噪比较低时，在估计信号相位时容易受到噪声尖峰的影响，导致相位估计出现大的误差，这些误差称为野值。由于野值的存在，导致了相位估计的均方误差变大。

考虑相位差为两个独立同分布的信号φ1，φM的差值，则相位差ΔφM估计的C-R下界为

(8)

由于方位估计θ为ΔφM和频率f的函数，对ΔφM求导后可得

(9)

频率f的估计均方误差为

(10)

式中：η为信道化处理后的信噪比；ΔT为积累时间。

θ对f求导得到

(11)

这样，可以得到干涉仪测向的方位θ估计值的C-R下界为

(12)

对于ΔT≥0.1 μs情况，此时，系统的测频分辨率在10 MHz左右，考虑最大阵间距在1 m量级，可以得到

(13)

即，由测频引起的方位估计误差可以忽略，这样可以得到方位θ估计值的近似C-R下界为

(14)

干涉仪测向误差与输入信噪比，信号波长，最长基线长度，入射角等参数均相关。

由于相位估计的非线性，导致干涉仪测向误差的概率分布仅是近似符合高斯分布，当信噪比较低的情况下，估计的方差将会大于C-R下界，产生野值。由于通常相位干涉仪系统需要通过多基线解相位模糊，单个天线信号相位的测量出现野值不但会影响最终的方位测量精度，还会影响解模糊的过程。为此，相位干涉仪的工作需要设置一定的信噪比门限(通常12 dB以上)，仅对达到信噪比门限的信号进行相位测量，同时也需要设置一些准则剔除解模糊失败后产生的方位野值，减少非线性引起的系统工作不稳定。

4 均匀阵列DBF测向误差

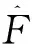
(15)

式中：N为参与谱估计的样点数，对于空间谱估计，N就是阵元数；η为单个天线的输入信噪比。

方位估计θ为空间频率F的函数，对F求导后可得

(16)

利用DBF可以提升接收信号信噪比N倍，则此时的频率测量的方差为

(17)

方位估计θ对f求导后可得

(18)

这样，可以得到均匀线阵测向的方位θ估计值的C-R下界为

(19)

对于单元间距较小，阵元数有限的雷达侦察应用场景，阵孔径通常在1 m以下，测频分辨率小于10 MHz,则有

(20)

即相比测相引起的误差，测频引起的误差可以忽略，得到近似的方位测量C-R下界

(21)

均匀线阵测向精度与输入信噪比，信号波长，阵物理孔径，入射角等参数均相关。

相比干涉仪测向，采用均匀阵列测向可以改善信噪比，在完成DBF处理后，可以得到N倍的信噪比提升，对应系统灵敏度可以提升10 lgNdB，如阵列为32元，系统灵敏度可以提升15 dB左右。

5 误差性能对比

对比干涉仪与均匀线阵天线的测向性能，为方便比较，以均匀线阵阵元间距d为基准，假设干涉仪最长基线长度为Kd，可以得到干涉仪的测向误差C-R下界为

(22)

整理后N元d间距均匀阵列DBF测向误差的C-R下界为

(23)

假设干涉仪天线与均匀阵天线采用相同的单元天线，对于同一辐射源，单元天线接收信号的性噪比η相同，对比两种测向体制C-R下界后可以得到

(24)

有以下结论：

1)干涉仪的测向误差C-R下界与基线长度的二次方成反比，均匀阵列DBF的测向误差C-R下界与基线长度的三次方成反比；

2)32元d间距均匀阵DBF测向能力与最大间距72d的干涉仪阵列相当；

3)干涉仪测向需要先检测信号有无，而后再测量信号相位差，处理过程无信噪比提升，不适用于小信噪比的情况；而均匀线阵先利用数字波束形成技术估计信号空间谱，之后进行信号检测与测向，测向与检测同步，经过波束形成后可以得到阵列增益，提高检测信噪比，所以适合小信噪比环境测向，具有更高的系统灵敏度。

表1进一步给出了干涉仪测向与DBF测向系统的优劣势对比以及适应环境分析。该综合分析便于工程人员对两种测向体制有更全面的认识。

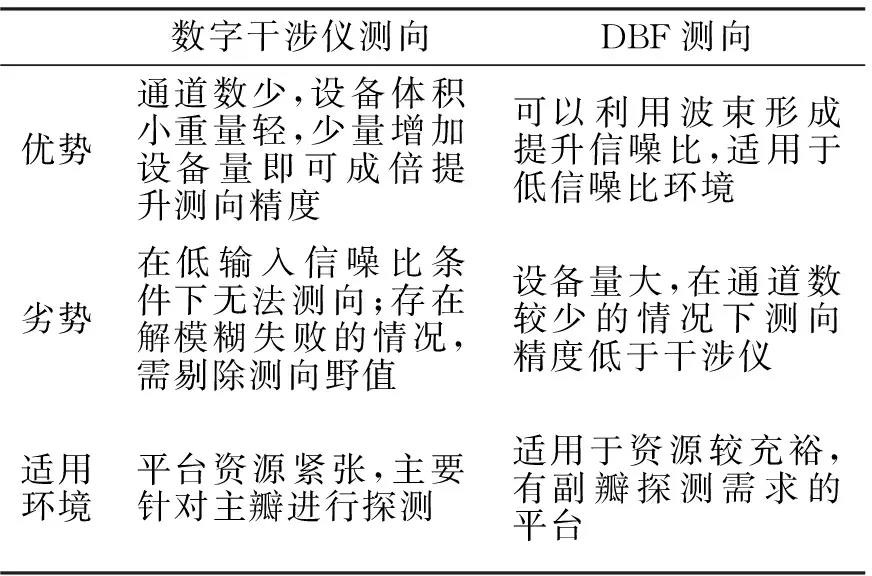
表1 干涉仪与DBF测向系统对比

6 结束语

对系统灵敏度的追求始终是电子侦察接收机的发展方向，随着微电子技术的快速发展，微波和数字电路的集成度大幅度提升，使得设备体积功耗大大降低， DBF由于其高灵敏度的特点，已经成为机载电子对抗系统设计的可选项。针对DBF设备量大，体积、重量、功耗以及散热等资源消耗大的情况，为解决DBF设备机载平台适装性问题，系统设计时可以做一些平衡。比如牺牲一部分瞬时空间覆盖能力，则可以采用子阵DBF的测向体制，设备量可以大幅降低，达到单元DBF的1/4甚至更少，此时系统的灵敏度和测向精度可以与单元DBF基本相当。

本文通过对噪声条件下测向误差方差的推导，获得误差方差C-R下界，在此基础上对比干涉仪和DBF的测向性能，从而为平台测向体制选择提供参考依据。需要注意的是，上述误差推导过程只针对由热噪声引起的误差进行分析，在工程应用中，方位测量设备的测向误差还与天线的相位一致性，单元方向图，接收通道的相位一致性以及结构安装误差等因素均密切相关。当阵面孔径达到一定规模以及信噪比满足一定量级后，由噪声引起的测量误差已经不是测向误差的主要来源。为此，需要在方位测量设备设计的过程中充分考虑到系统校准，包括几何结构校准，天线方向图以及相位中心校准，接收通道幅相一致性校准，以减少这类固定偏差对测量误差的影响。

[1] 胡来招．雷达侦察接收机设计[M]．北京：国防工业出版社，2000． HU Laizhao, Design for radar reconnaissance receivers[M]. Beijing: Publishing House of National Defense Industry, 2000.

[2] 唐永年. 雷达对抗工程[M]. 北京：北京航空航天大学出版社，2012. TANG Yongnian, Radar ECM[M]. Beijing: Publishing House of Beijing University of Aeronautics and Astronautics, 2012.

[3] 阳 凯, 等．宽带干涉仪阵列布局设计[J]. 电子信息对抗技术，2015，30(4): 54-57. YANG Kai, et al. A baseline dsign method of wideband interferometer[J]. Electronic information warfare technology, 2015, 30(4): 54-57.

[4] 杨 晶, 等. 相位干涉仪参差基线解模糊算法研究[J]. 航天电子对抗, 2013，28(3): 31-34. YANG Jin, et al. Research on algorithm of solving stagger-baseline interferometer phase difference ambiguity[J]. Aerospace Electronic Warfare, 2013, 28(3): 31-34.

[5] 张刚兵, 等. 基线比值法相位解模糊算法[J]. 南京航空航天大学学报, 2005,40(5): 665-669. ZHANG Gangbin, et al. Unwrapping phase ambiguity algorithm based on baseline ratio[J]. Journal of University of Aeronautics and Astronautics, 2005, 40(5): 665-669.

[6] 马银玲, 等. 基于DBF的比幅测向方法研究[J]. 舰船电子对抗，2014，37(2) : 91-93. MA Yinling, et al. Research into amplitude comparison DF method based on DBF[J]. Shipboard Electronic Warfare, 2014, 37(2): 91-93.

[7] 李春利. DBF体制接收系统的设计[J]. 现代雷达, 2015, 37(1): 63-66. LI Chunli. Design for DBF-system receiver[J]. Modern Radar, 2015, 37(1): 63-66.

[8] 李杰涛, 等. DBF同时多波束测角方法研究及工程实现[J]. 火控雷达技术，2013，42(2): 19-22. LI Jietao, et al. Study on DBF simultaneous multibeam angle measuring method and its implementation in engineering[J]. Fire control radar technology, 2013, 42(2): 19-22.

[9] Steven M.Key. 统计信号处理基础--估计与检测理论[M]. 北京：电子工业出版社，2003. STEVEN M. Key. Fundamentals of statistical signal processing-stimation and detection theory[M]. Beijing: Publishing House of Electronic Industry, 2003.

夏鸿宝 男，1982年生，工程师。研究方向为雷达对抗总体技术。

周国永 男，1982年生，工程师。研究方向为雷达对抗总体技术。

左登朝 男，1974年生，高级工程师。研究方向为雷达对抗总体技术。

吴上游 男，1958年生，研究员。研究方向为雷达对抗总体技术,主持多型雷达对抗设备的研制。

舒 汀 男，1981年生，博士，助理研究员。研究方向为雷达与电子战射频仿真技术，实时信号处理系统设计与开发，相控阵雷达数字波束形成技术等。

Comparison of Direction-finding Performance Between Linear Array Interferometer and Uniform Linear Array DBF

XIA Hongbao1，ZHOU Guoyong1，ZUO Dengchao1，WU Shangyou1，SHU Ting2

(1. Nanjing Corad Corporation, Nanjing 211100, China) (2. Shanghai Key Laboratory of Intelligent Sensing and Recognition,Shanghai Jiao Tong University, Shanghai 200240, China)

The system composition, operating principle and process flow of linear array interferometer and uniform linear array DBF are introduced firstly. Then, the Cramér-rao lower bounds(CRLB) for each method of direction-finding are deduced. A comparison of direction-finding performance is done through CRLB. An analysis of application scenarios is done according to their features. Some conclusions are significant and valuable to engineers in system design.

digital interferometer direction-finding; DBF direction-finding; C-R lower bound

10.16592/ j.cnki.1004-7859.2016.12.006

国家自然科学基金资助项目(61571294)；航空科学基金资助项目(2015ZD07006)

夏鸿宝 Email：hongbaoxia@139.com

2016-09-15

2016-11-18

TN957

A

1004-7859(2016)12-0031-05