子阵级数字波束形成抗多主副瓣干扰及测角技术

舒 汀，陈新竹，余啟波，郁文贤

(上海交通大学 上海市智能探测与识别重点实验室， 上海 200240)

·DBF在现代雷达中的应用·

子阵级数字波束形成抗多主副瓣干扰及测角技术

舒 汀，陈新竹，余啟波，郁文贤

(上海交通大学 上海市智能探测与识别重点实验室， 上海 200240)

对于大型的二维相扫雷达天线阵列，数字波束形成通常在子阵上完成，以减少数字接收机的数量并降低成本。基于子阵级数字波束形成，文中提出了一种改进的自适应信号处理架构，在低成本的情况下，同时抑制多个主副瓣干扰，并保持对目标的单脉冲测角精度。首先，每个子阵内部形成非自适应的波束并转化为数字输出；再利用行和列波束的分维特性，在子阵级形成自适应波束，进行干扰抑制处理；最后，分别将各个行或列波束合成为全阵列的俯仰或方位和差波束，用于目标的单脉冲测角。与传统的四通道抗主瓣干扰相比，该方法在合成和差波束前，基于子阵级数字波束完成自适应干扰的抑制。因此，充分利用了有限的自由度，挖掘了子阵级数字阵列抗同时多个主副瓣干扰的能力。还结合相控阵雷达实例，给出了仿真结果，验证了该方法的有效性。总的来说，所提出的阵列信号处理架构，在降低系统复杂度和成本的同时，大大提高了雷达系统的抗干扰能力。

子阵级数字波束形成；多干扰抑制；单脉冲测角

0 引 言

现代雷达采用相控阵技术，通过电子扫描可灵活精确地控制波束指向，具有搜索和跟踪多个目标的能力，进而推动了多功能雷达的产生与发展。数字波束形成技术则基于数字接收机使用数字信号处理算法代替了传统的模拟器件来合成波束，是新一代阵列雷达的重要突破之一。该技术可用于实现同时多波束、自适应信号处理、精确的角度估计以及阵列自我修复等[1]。但是，二维相位扫描的平面相控阵接收天线由成千上万个阵元构成，采用全数字阵在阵元级实现数字波束形成会造成设备量急剧增大和成本剧增，且数据量巨大，对软硬件数据处理能力的要求极高[2]。在实际的相控阵雷达系统中，比较合理的解决方法是将整个平面相控阵分成若干个子阵，合成子阵波束后转化为数字输出，以减少数字接收机的数量，降低成本。该结构是模拟和数字波束形成的混合模式[3]：非自适应的模拟波束形成在子阵内部由每个阵元的T/R组件移相器完成；每个子阵输出的模拟信号转化为数字信号后，合成所需的数字波束。

相控阵雷达工作在复杂的电磁环境中，面临各类干扰信号，会使得雷达性能下降，无法对目标进行探测、定位和跟踪[4]。采用自适应数字波束形成技术后，雷达抗干扰的能力大大提高。实际上，相控阵雷达的抗干扰能力可以用空域自由度来衡量，空域自由度由通道数字接收机的个数决定。理论上，自由度的大小决定了雷达可以消除的最大干扰数目。目前为止，抗副瓣干扰技术的研究和应用均已成熟，抗主瓣干扰问题则面临更大的挑战。Applebaum[5-6]提出基于四通道波束的自适应数字波束形成架构，可以在消除主瓣干扰的同时保持对目标测角的精度。在该结构中，系统在方位或俯仰维只有两个自由度，因此，只能消除一个主瓣干扰。基于这四个波束，另一种方法是最大似然估计法搜索目标角度[7]，但主要缺陷在于完成搜索的计算量巨大，故很难在实际应用中实现。同时，存在主副瓣干扰时，文献[8]提出了一个两级的信号处理架构，分别抑制副瓣和主瓣干扰，但需已知主瓣干扰的部分信息。文献[9]则提出一个基于全数字阵的同时抗主副瓣干扰的架构，但需先在子阵内部完成自适应数字波束形成，再形成全阵列的和差波束。上文已提到，这样的全数字阵造价昂贵系统复杂，尤其对于大阵列而言难以实现。

本文针对基于数字子阵架构的大型二维相扫阵列天线，提出了一个同时抑制主副瓣干扰的处理架构。在子阵内部，由T/R组件将阵元接收到的信号合成非自适应的模拟波束输出，将子阵输出转化为数字信号后，在子阵级合成每一行和每一列的自适应波束输出，在此过程中已消除了多个主副瓣干扰。然后，沿垂直或水平方向，将各行或各列波束合成为全阵列的俯仰或方位和差波束输出，用于目标的单脉冲测角。该方法能够在数字子阵架构下，利用有限的自由度，同时抑制多个主副瓣干扰。

本文第二节介绍了子阵级数字波束形成的基本原理，第三节详细说明了该改进型自适应数字波束形成抗多个主副瓣干扰的信号处理架构，第四节给出仿真结果，其抗多主副瓣干扰的性能优异。

1 子阵数字波束形成原理

模数混合的阵列天线结构中，在每个子阵内，由T/R组件实现模拟移向，因此，形成的子阵波束都是非自适应的。模拟子阵波束的输出在数字接收机中转化为数字信号，与全数字阵相比，大大减少了数字接收机的数量。第m个子阵的波束方向图为

(1)

式中：N为第m个子阵中阵元的个数，此时无幅度加权；(u0,v0)为波束指向的方位余弦。(xn,yn)为每个阵元相对于整个阵列中心的坐标，也可以写作

(2)

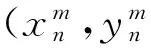
全阵列波束方向图为

(3)

式中：wm为乘以每个子阵输出的加权系数。将子阵输出乘以多组权向量即可同时形成多波束，因此，数字波束形成相比于模拟方式更为灵活。

如式(2)所示，将M个子阵输出加权后相加即可形成全阵列波束，自由度也由M降为1。为了充分利用此混合子阵系统中的自由度，本文考虑在形成全阵列和差波束前，做子阵级的自适应数字信号处理，以消除更多的主副瓣干扰。

2 改进的子阵级数字波束形成处理结构

以一个矩形阵为例，如图1所示，该阵列天线被划分成16个相同的子阵。对于改进后用于抑制多主副瓣干扰的信号处理流程如图2所示：第一步，在阵元级采用非自适应的模拟波束形成，并将子阵输出转化为数字信号；第二步，将子阵的波束输出作为输入，合成自适应行和列波束，由于每行或每列有四个子阵波束，因此最多可以消除三个干扰；第三步，沿着垂直或水平方向，分别将各个行或列波束形成为全阵列的俯仰或方位和差波束；最后，完成对目标的二维单脉冲测角。

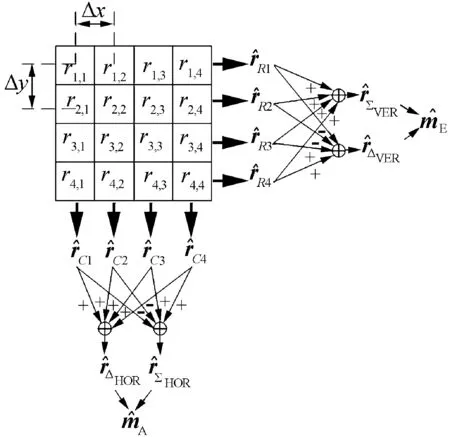
图1 改进的子阵级自适应波束形成算法

2.1 子阵级自适应行列波束形成抗多个干扰

在每一行或列中，有四个相同的子阵，可视为一个均匀线阵。在第i行(i=1,2,3,4)，设子阵波束输出的数字信号为

(4)

选取其中一个子阵的波束作为主波束，其他三个作为辅助波束，最多可以消除三个干扰。则第i行波束的自适应输出为

(5)

式中：自适应输出用符号“^”表示，自适应权值W(R)为

(6)

可由LCMV算法[10]得到。所得到的第i行的自适应行波束方向图沿uJ形成三条凹陷，对应干扰源的俯仰角φJ，即三个干扰在自适应行波束中沿俯仰维被抑制。对于不同行的自适应波束形成，权矢量近似相等，因为不同行之间，位置对应相同的子阵波束方向图间，有确定的相位差关系，该相位差由子阵中心坐标决定。

同理，第i列(i=1,2,3,4)的自适应列波束形成的方法相似，其自适应列波束的输出为

(7)

该列的子阵输出的数字波束向量为

(8)

第i列的自适应列波束方向图沿vJ形成三条凹陷，对应干扰源的俯仰角θJ，即三个干扰在自适应列波束中沿方位维被抑制。对于不同列的自适应波束形成，权矢量也近似相等。

2.2 全阵列和差波束形成单脉冲测角

将四行或四列的波束输出，作为全阵列波束的输入，沿着垂直方向或水平方向相加减，即可得到全阵列的俯仰或方位和差波束。用差波束比和波束，除干扰源方向外，即可得到无失真的单脉冲曲线，并精确测量目标角度。

对于俯仰维测角，将各行波束输出沿垂直方向相加得到垂直和波束ΣVER，相减得到垂直差波束ΔVER，表达式分别为

(9)

可视为垂直方向上均匀直线阵的和差波束形成。

对于方位维测角，将各列波束输出沿水平方向相加得到水平和波束，相减得到水平差波束，表达式分别为

(10)

可视为水平方向上均匀直线阵的和差波束形成。

俯仰和方位维的自适应单脉冲比分别为

(11)

而传统的单脉冲比由全阵列的和差波束比得到，如下

(12)

注意，同一行或列中，任意两个子阵的波束方向图可表示为

(13)

式中：Δx和Δy分别为两个相邻子阵中心沿水平和垂直方向的间距，如图2所示。将式(13)代入式(12)，传统的单脉冲曲线可化简为

(14)

由式(14)可得，全阵列的单脉冲比与任意行或列阵的单脉冲比等价。

将式(5)和式(7)代入式(11)，自适应单脉冲比也可化简为

(15)

显然，除了沿着干扰源的方向余弦uJ和vJ处，俯仰维和方位维的自适应单脉冲比与原单脉冲比相同。说明该算法在消除多干扰后，对目标仍能够保持精确的测角精度。

3 仿真与分析

下面给出本文提出的基于子阵级自适应波束形成算法抗多个主副瓣干扰及目标测角应用于具体雷达天线阵列的仿真结果。设一个平面相控阵由4×4个相同的子阵组成，每个子阵含有8×8个阵元，按三角形栅格阵排列，间距均为半波长，如图2所示。雷达阵列天线的波束指向为(0°,0°)。没有幅度加权。

设目标的方位角及俯仰角为(-0.2°，-0.3°),其方向余弦为(-0.003 5,-0.005 2)。三个干扰的角度分别为(1.2°,0.8°), (-1°,-1°)和(-3°, 4°)，其方向余弦分别为(0.020 9,0.014 0), (0.017 4,0.017 5)和(-0.052 2, 0.069 8)。在子阵输出端，SINR为-25 dB。显然，前两个干扰都在主瓣内，与目标间的角度差很小。

3.1 自适应行列波束方向图及多干扰对消

利用每行或每列的四个子阵输出的波束，形成自适应的行或列波束，如图3所示。显然，自适应列波束中沿三个干扰的方向余弦uJ形成了三条零陷，自适应行波束中沿三个干扰的方向余弦vJ形成了三条零陷。也就是说，三个干扰在两维分别被消除了。

3.2 自适应全阵列和差波束方向图及单脉冲曲线图

沿着水平或垂直方向将自适应列波束或行波束相加减，得到了全阵列的自适应和差波束，如图4所示。由于全阵列的和波束具有更高的增益，因此，水平和波束或垂直和波束的输出可用于检测目标和测距。

图4 和差波束方向图

自适应单脉冲比的保形特性可从图5中观察到。与图5a)相比，除了沿着主瓣干扰的两处uJ零陷外，图5c)中的自适应俯仰单脉冲比与原单脉冲比相同；与图5b)相比，除了沿着主瓣干扰的两处vJ零陷外，图5d)中的自适应方位单脉冲比与原单脉冲比也相同。

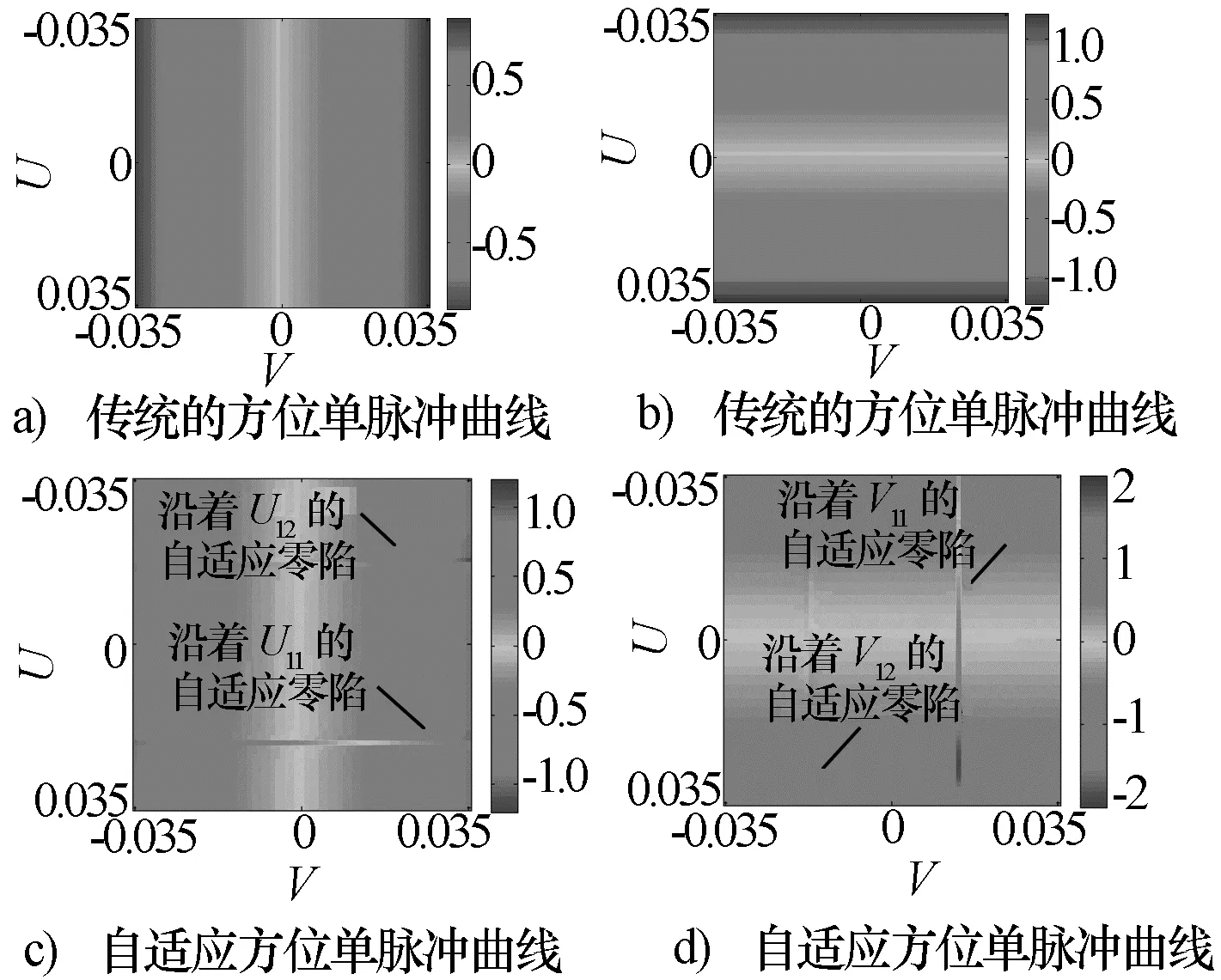
图5 单脉冲二维曲线图

3.3 单脉冲测角性能评估

最终，作出干扰消除后，对目标进行角度估计的散点图，如图6a)所示。该图是相同干扰场景SIR=-34 dB下的100次仿真结果。目标的真实位置用浅色圆点标出，干扰的位置用深色圆点标出，对目标的测角结果用十字叉标出。显然，测角结果十分接近真实目标位置，说明本文提出的算法，在存在多主副瓣干扰的场景下，仍获得了精确的测角结果。如图6b)所示，如果SIR增大到-30 dB，测角精度更高。

图6 单脉冲测角结果

另外，测角的精确度也取决于目标所在主瓣区域的具体位置。很显然，目标与干扰之间在角度上越靠近，目标回波的信号损失越大，测角精度越差。图7给出了相同SIR下，目标在主瓣的各个不同位置处时，本文提出的算法得到的测角性能。在图7a)中，目标处于其他大部分位置时，方位测角的RMSE都很低，除非目标方位角与任一主瓣干扰的方位角吻合，即自适应行波束中两条零陷的位置。图7b)中给出的俯仰测角性能相似。注意，图7b)中沿着两个主瓣干扰方位角的两条水平区域处，俯仰测角误差也较大。这是因为目标的方位角φT最终由方向余弦值uT计算得到，而由方位角φT和俯仰角θT共同决定，因此，图7a)中的条带也保留在了图7b)中。图7c)定量的给出了，当SIR提高时，测得目标方向余弦RMSE值，即测角误差的变化情况。总的来说，存在多个干扰时，本文提出的自适应波束形成架构，对主瓣中的大部分区域仍然有较高的单脉冲测角性能。

4 结束语

二维相扫的平面相控阵由成千上万个阵元构成，通常将整个平面相控阵分成若干个子阵。非自适应的模拟波束形成在子阵内部由每个阵元的T/R组件移相器完成；每个子阵输出的模拟信号转化为数字信号后，合成所需的数字波束，数字接收机的数量减少成本大大降低的同时，自由度也有所减少。

而现代相控阵雷达工作在复杂的电磁环境中，面临着消除多个主副瓣干扰的难题，否则无法对目标进行探测、定位和跟踪。本文提出了一种子阵级DBF的同时多个主副瓣干扰抑制处理技术，该方法在每行和每列利用多个子阵波束消除多个主副瓣干扰，然后形成全阵列和差波束，在自由度有限的情况下，仍能消除多个主副瓣干扰，并保持单脉冲测角精度，文章通过计算机仿真验证了方法的性能。本文的方法兼顾算法的综合性能和系统的复杂度，具有较好的工程实用价值。

[1] 罗 敏. 多功能相控阵雷达发展现状及趋势[J]. 现代雷达, 2001, 33(9): 14-18. LUO Min. Development status and trend of MPAR[J]. Modern Radar, 2001,33(9): 14-18.

[2] 张光义，赵玉杰. 相控阵雷达技术[M]. 北京: 电子工业出版社，2006. ZHANG Guangyi, ZHAO Yujie. Phased array radar technology[M]. Beijing: Publishing House of Electronic Industry, 2006.

[3] NICKEL U. Fundamentals of signal processing for phased array radar[R]. Germany: GAN-FHR Research Inst for High Frequency Physics and Radar Techniques Wachtberg, 2006.

[4] 胡 进, 李建勋, 刘 笑. 地面情报雷达抗有源干扰能力的定量描述[J]. 现代雷达, 2015, 37(10): 5-10. HU Jin, LI Jianxun, LIU Xiao. Quantitative description of anti-active jamming ability for ground information radar[J]. Modern Radar, 2015, 37(10): 5-10.

[5] 胡 航, 张 皓, 宗成阁, 等. 子阵级自适应单脉冲的四通道主瓣干扰抑制[J]. 电波科学学报, 2009, 24(5): 820-825. HU Hang, ZHANG Hao, ZONG Chengge, et al. Four-channel mainlobe jamming suppression for adaptive monopulse at subarray level[J]. Chinese Journal of Radio Science, 2009, 24(5): 820-825.

[6] HOFFMAN J B, GALEBACH B L, HOHNSON K R. Four-channel monopulse for main beam nulling and tracking[C]// Proceedings of IEEE National Radar Conference. [S.l.]: IEEE Press, 1998: 94-98.

[7] FARINA A, GOLINO G, TIMMONERI L. Maximum likelihood estimator approach to determine the target angular co-ordinates in presence of main beam interference: application to live data acquired with a microwave phased array radar[C]// IEEE International Radar Conference. [S.l.]: IEEE Press, 2005: 61-66.

[8] YU K B, MURROW D J. Adaptive digital beamforming for angle estimation in jamming[J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(2): 508-523.

[9] YU K B. Adaptive sub-array digital beamforming and deterministic sum and difference beamforming with jamming cancellation and monopulse ratio perservation[P]. U.S. Patent: 6 661 362 B2, 2003.

[10] MANOLAKIS D G, INGLE V K, KOGON S M. Statistical and adaptive signal processing[M]. Norwood, MA, USA: Artech House, 2005.

舒 汀 男，1981年生，博士，助理研究员。研究方向为雷达与电子战射频仿真技术，实时信号处理系统设计与开发，相控阵雷达数字波束形成技术等。

Multiple Jamming Cancellation Using Adaptive Subarray DBF for Angle Estimation

SHU Ting，CHEN Xinzhu，YU Kai-bor，YU Wenxian

(Shanghai Key Laboratory of Intelligent Sensing and Recognition,Shanghai Jiao Tong University, Shanghai 200240, China)

An enhanced array processing architecture using adaptive digital beamforming at subarray level is proposed for monopulse angle estimation in presence of mainlobe and sidelobe jammings. First, in order to reduce the receiver count, fixed analog beamforming is performed at element level and sub-array outputs are converted to digital signals. Then, adaptive row and column digital beams are formed at subarray level to adaptively cancel multiple jammings. Finally, monopulse sum and delta beamformer follows using row and column beams in vertical and horizontal dimension respectively for elevation and azimuth angle estimation. Compared with the conventional processing with four beams, adaptive digital beamforming is performed with subarray beams prior to sum and delta beamforming, that is, more digital degrees of freedom are exploited. Thus the capability of cancelling multiple electronic jammings simultaneously is provided. Additionally, simulation results of angle estimation are shown. To sum up, this technique is developed to demonstrate the potential of digital beamforming at subarray level with low cost and more facility.

subarray digital beamforming; multiple jamming canellation; monopulse angle estimation

10.16592/ j.cnki.1004-7859.2016.12.004

国家自然科学基金资助项目(61571294)；航空科学基金资助项目(2015ZD07006)

陈新竹 Email：chenxinzhu_92@163.com

2016-09-20

2016-11-21

TN973

A

1004-7859(2016)12-0022-05