频域内海洋资料浮标垂荡运动特性研究

王华洁，孙金伟, *，邵萌，范秀涛

(1. 山东省科学院海洋仪器仪表研究所, 山东省海洋环境监测技术重点实验室，山东 青岛 266001； 2.中国海洋大学工程学院，山东省海洋工程重点实验室，山东 青岛 266100)

【海洋科技与装备】

频域内海洋资料浮标垂荡运动特性研究

王华洁1，孙金伟1, 2 *，邵萌2，范秀涛1

(1. 山东省科学院海洋仪器仪表研究所, 山东省海洋环境监测技术重点实验室，山东 青岛 266001； 2.中国海洋大学工程学院，山东省海洋工程重点实验室，山东 青岛 266100)

随波性作为海洋资料浮标的重要设计参数，影响着波浪参数的测量准确度。本文应用三维势流理论计算了圆盘浮标体的附加质量、兴波阻尼系数等水动力系数以及波浪激励力，基于单自由度运动方程研究了自由浮标的垂荡响应。考虑锚链垂向弹性回复刚度系数对浮标垂荡的影响，研究了两种类型系泊浮标在波浪中的垂荡运动响应。研究发现，直径3 m浮标较直径10 m浮标具有更好的随波性，且锚链对3 m浮标的垂荡运动的影响较10 m浮标更为显著。研究结果对波浪传感器的参数修正具有重要意义。

海洋资料浮标；垂荡响应；弹性系数；频域

海洋资料浮标是锚泊在特定海域位置的水面水文气象观测站，波浪是众多水文气象观测要素中重要的一项，为保证不同周期范围内的波浪测量准确度，要求海洋资料浮标要具有良好的随波性。浮标的随波性主要体现在波浪作用下浮标的垂荡自由度运动，因此精确预报浮标在不同波浪频率下的垂荡运动响应，揭示其垂荡运动规律，对于该类浮标的波浪传感器参数修正、提高数据测量准确度具有重要意义。

势流理论广泛地应用于预报浮体在波浪中运动的性能，能够得到较为理想的浮标垂荡运动响应预报结果。海洋资料浮标是由柔性锚系和刚性浮体组成的海洋浮式结构物，对于该类浮式结构，国内外学者关注较多的是深水大尺度浮式钻井平台、采油平台和深水储/卸油浮筒等，研究重点集中在浮体的六自由度运动响应以及锚系受力，而对于近海海洋资料浮标垂荡运动响应特征的研究较少。

Bunnik等[1]、Cozijin等[2-3]对深水多锚腿悬链系泊的储/卸油浮筒的运动响应进行了耦合动力分析和模型试验研究。Umar等[4]采用时域方法研究了多点系泊浮标在波浪一阶和二阶激励力作用下的单自由度纵荡响应。Idris等[5]在时域内对系泊浮标开展了耦合动力数值分析，并进行了实验验证。Leonard等[6]采用三维耦合分析方法研究了浮标与锚系之间的耦合作用。陈小红等[7]采用频域方法进行了单点系泊浮标的动力分析，研究了锚泊线与浮标体之间的耦合关系。缪泉明等[8]提出了一种快速计算锚链动力的简化分析方法，应用脉冲响应的卡明斯运动方程，在时域内对极限海况下三锚系统浮标的运动和锚系受力进行了数值模拟估算。范秀涛等[9]用谱分析方法研究了大型海洋资料浮标的垂荡和横摇运动响应，但是研究中没有考虑锚系的影响。张继明等[10]利用浮标模型试验修正横摇阻尼系数，在频域内对海洋资料浮标的横摇运动响应进行了数值仿真研究，同样没有考虑锚系的作用。

对于深水浮式结构，由于锚系长度大，锚系的惯性及阻尼对浮体的运动有明显影响，二者存在着强烈的耦合作用，需要进行耦合运动分析[11]。但是耦合分析方法复杂、计算量大，对于近海浅水单点系泊资料浮标运动分析显得并不经济。浮体在波浪中的运动响应分析可在时域或频域内进行，时域方法能够处理非线性问题，精度高，但是计算量大、计算耗时；频域分析方法适用于线性或弱非线性问题，计算快速简便、效率高，适合于非线性特征并不显著的浮体垂荡运动的分析计算。

本文在频域内研究了单点系泊海洋资料浮标在波浪中的垂荡运动响应,应用三维势流理论计算了浮标体的附加质量、势流阻尼系数及波浪激励力。由于浮标的对称性，其他自由度与垂荡之间没有耦合影响，本文建立浮标体单自由度垂荡运动方程，求解自由浮标的垂荡响应。对于系泊浮标，考虑锚链垂向弹性系数对浮标垂荡运动的影响，研究了在水深15 m时，直径10 m和3 m两种不同类型浮标的垂荡运动特性。本文的研究结果对考虑浮标垂荡运动影响的波浪传感器参数修正具有重要意义。

1 频域运动方程

1.1 自由浮标运动方程

在浮体水动力运动特性研究中，一般将浮体认为是具有6个运动自由度的刚体。浮标在多种载荷的作用下保持运动平衡，作用力包括惯性力、阻尼力、回复力以及波浪激励力。根据牛顿第二定律，自由浮标在频域内运动微分方程如下：

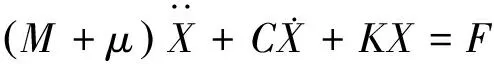
(1)

其中，M是浮标质量矩阵，μ是浮标的附加质量矩阵，C是势流阻尼系数矩阵，K是静水回复刚度矩阵，F是波浪激励力矩阵，X是浮标运动响应矩阵。其中附加质量μ、势流阻尼系数C以及波浪激励力F可由势流理论[12]计算得到。

1.2 质量与回复刚度矩阵

建立浮标的质量模型，其中坐标原点在浮标底部中心位置，X轴与Y轴位于浮标底部平面，Z轴竖直向上。考虑自由度之间的耦合作用，质量矩阵M的表达式如下：

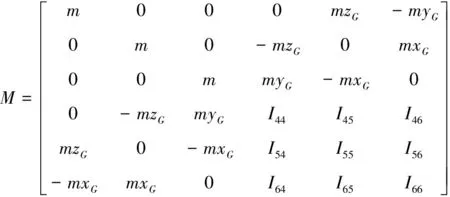
(2)

式中，m是浮标体质量，xG、yG和zG是浮标重心坐标，Iij是浮标质量惯性矩。

回复刚度矩阵K可由流体静力学计算得到，其表达式如下：

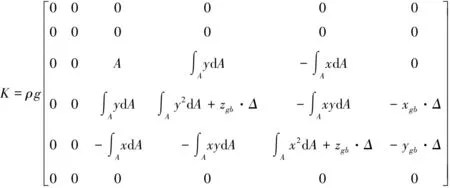
(3)

式中，ρ为流体密度，A是浮标水线面面积，Δ为浮标排水量，xgb、ygb和zgb为浮标浮心与重心之间的距离。

1.3 附加质量与阻尼

浮标在波浪力作用下产生运动，其运动的结果将产生一个辐射速度势，从而改变速度场的分布，使浮标受到一个附加水动力载荷。由于该载荷与浮标运动的速度和加速度成正比，所以通常以附加质量和阻尼的形式表示，其表达式如下：

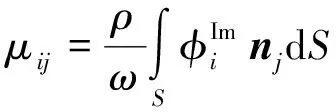
(4)

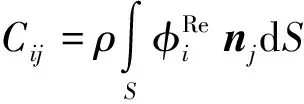
(5)

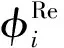
1.4 运动方程简化

1.4.1 自由浮标运动方程

浮标在规则简谐波激励下实现稳态运动时，波浪力和运动响应可表示成如下形式：

F=feiωt，

(6)

X=xeiωt，

(7)

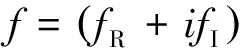
横向对称结构物的6个耦合运动方程可以简化为两组方程，一组是纵荡、垂荡和纵摇的3个耦合方程；另一组是横荡、横摇和艏摇的耦合方程。横向运动(横荡、艏摇和横摇)与垂向和纵向运动之间没有耦合效应[13]。由于浮标是双轴对称的圆盘结构，因此，附加质量μ31，μ35以及势流阻尼系数C31，C35均为0；同时由公式(3)可知，静水回复刚度系数K31，K35也为0，即纵荡与垂荡以及纵摇与垂荡之间没有耦合作用，浮标的垂荡响应可通过求解单自由度垂荡方程获得。

将式(6)和(7)代入式(1)，整理得到浮标单自由度垂荡响应运动方程如下：

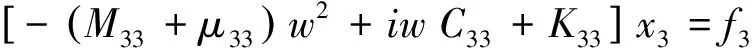
(8)

1.4.2 系泊浮标运动方程

海洋资料浮标采用全锚链的单点悬链式系泊方式。考虑到浮标所处水深较浅，计算中忽略锚链与浮标之间的动力耦合作用，仅考虑锚链的垂向弹性系数对浮标垂荡运动的影响。

锚系的垂向弹性系数可根据悬链线理论计算求解。若不考虑浮标静态偏移，那么锚系的垂向弹性系数即为锚系的单位长度水下重量。将锚链垂向弹性系数引入浮标运动方程，即可求解系泊浮标在海洋环境条件激励下的运动响应。系泊浮标在波浪中的运动方程如下：

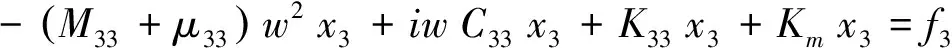
(9)

式中，Km是系泊锚链的垂向弹性系数。

2 计算结果及讨论

2.1 浮标参数

本文的研究对象是直径10 m和3 m的圆盘型浮标。图1和图2分别是10 m和3 m浮标的几何尺寸，表1和表2是浮标的质量参数。

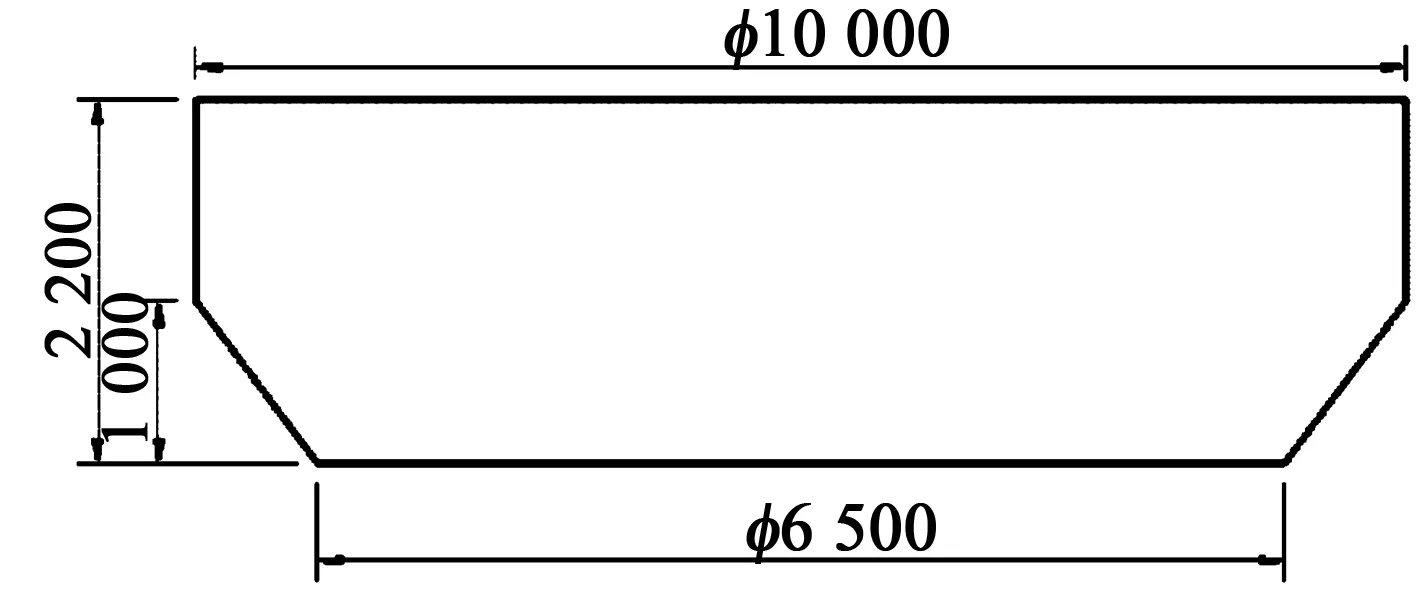
单位：mm图1 10 m浮标几何尺寸Fig.1 Size of the 10 m diameter buoy

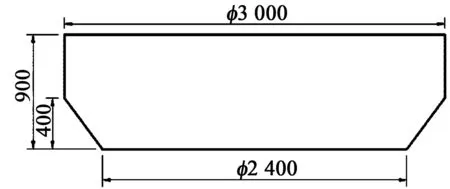
单位：mm图2 3 m浮标几何尺寸Fig.2 Size of the 3 m diameter buoy

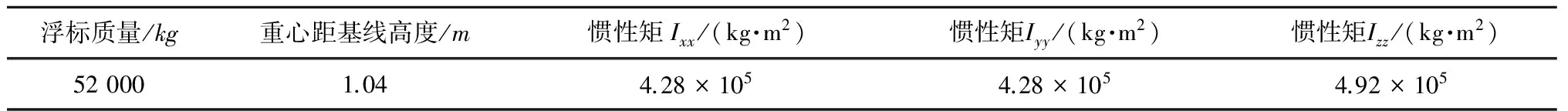
浮标质量/kg重心距基线高度/m惯性矩Ixx/(kg·m2)惯性矩Iyy/(kg·m2)惯性矩Izz/(kg·m2)520001．044．28×1054．28×1054．92×105

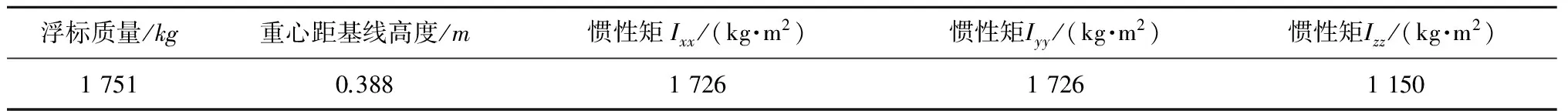
表2 3m浮标质量参数

2.2 浮标水动力计算结果

基于势流理论，在频域内求解了浮标体的水动力参数，分析中只考虑波浪作用，波浪入射角为0°。图3和图4是10 m和3 m浮标垂荡自由度附加质量曲线，图5和图6是垂荡自由度势流阻尼系数曲线，图7和图8是垂荡自由度的波浪激励力RAO(响应幅值算子)曲线。图9和图10是3 m浮标垂荡-纵荡耦合自由度附加质量和垂荡-纵荡耦合自由度势流阻尼系数曲线。根据浮标质量以及频域计算获得的浮标附加质量和静水回复刚度，可以得到浮标的垂荡固有周期。经计算，10 m浮标的垂荡固有周期为3.15 s，3 m浮标的垂荡固有周期为1.82 s。

图3 10 m浮标垂荡附加质量Fig.3 Heave added mass of the 10 m diameter buoy

图4 3 m浮标垂荡附加质量 Fig.4 Heave added mass of the 3 m diameter buoy

图5 10 m浮标垂荡势流阻尼系数Fig.5 Heave potential damping coefficients of the 10 m diameter buoy

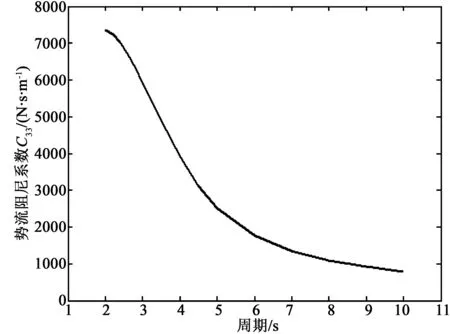
图6 3 m浮标垂荡势流阻尼系数Fig.6 Heave potential damping coefficients of the 3 m diameter buoy

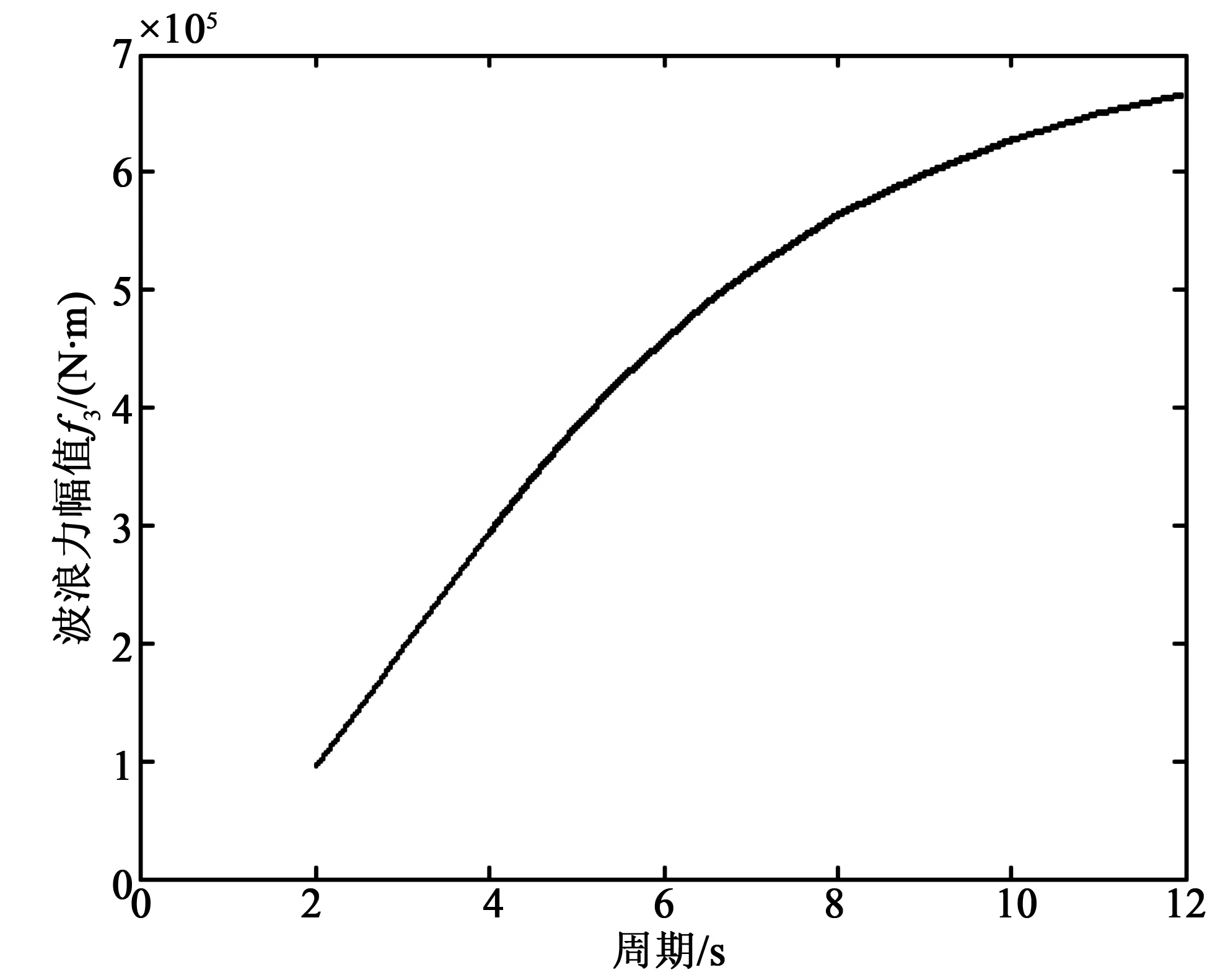
图7 10 m浮标垂荡波浪力幅值Fig.7 Heave wave exciting force amplitude of the 10 m diameter buoy

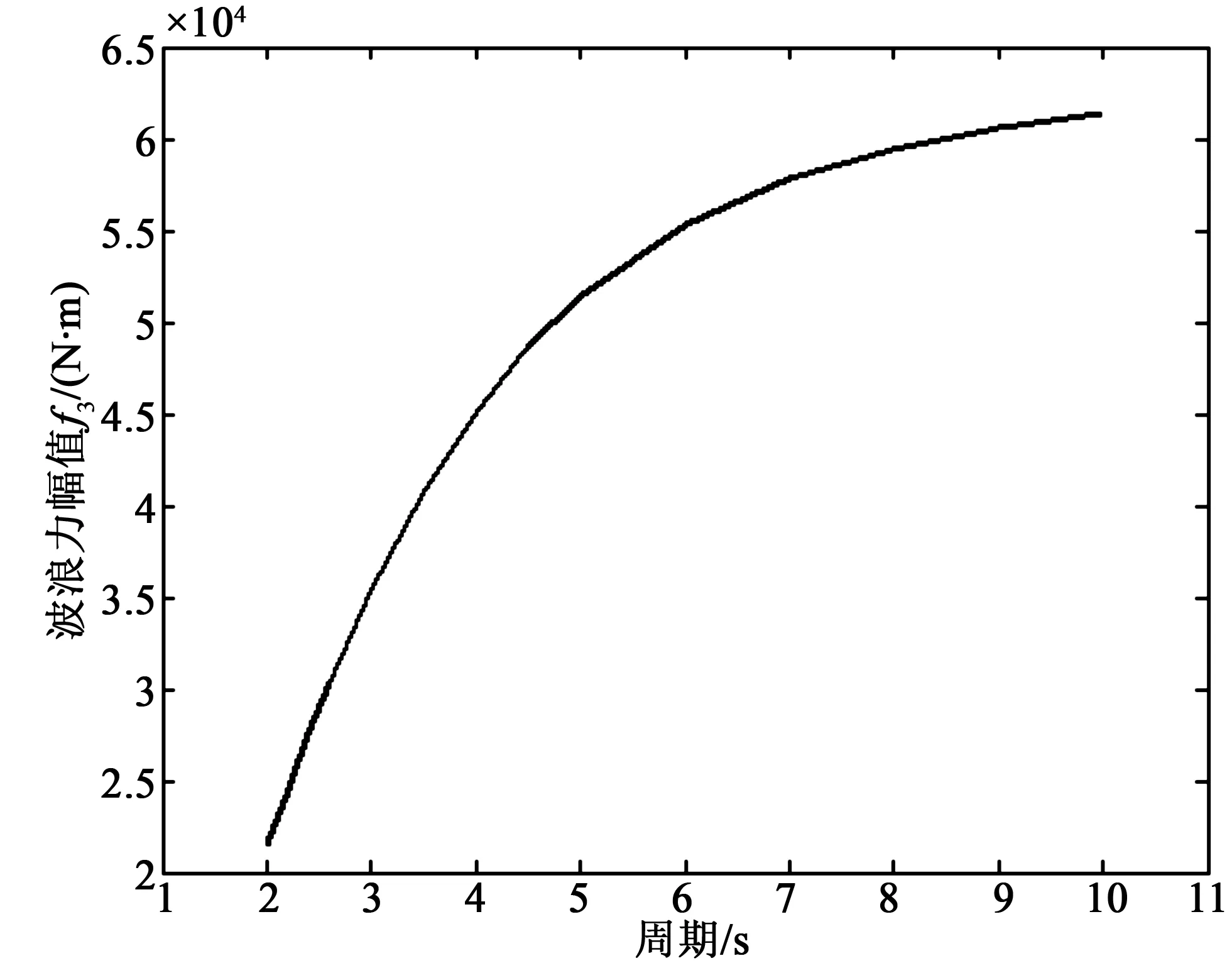
图8 3 m浮标垂荡波浪力幅值Fig.8 Heave wave exciting force amplitudeofthe3m diameter buoy

图9 3 m浮标垂荡-纵荡耦合自由度附加质量Fig.9 Coupled heave-surge added mass of the 3 m diameter buoy

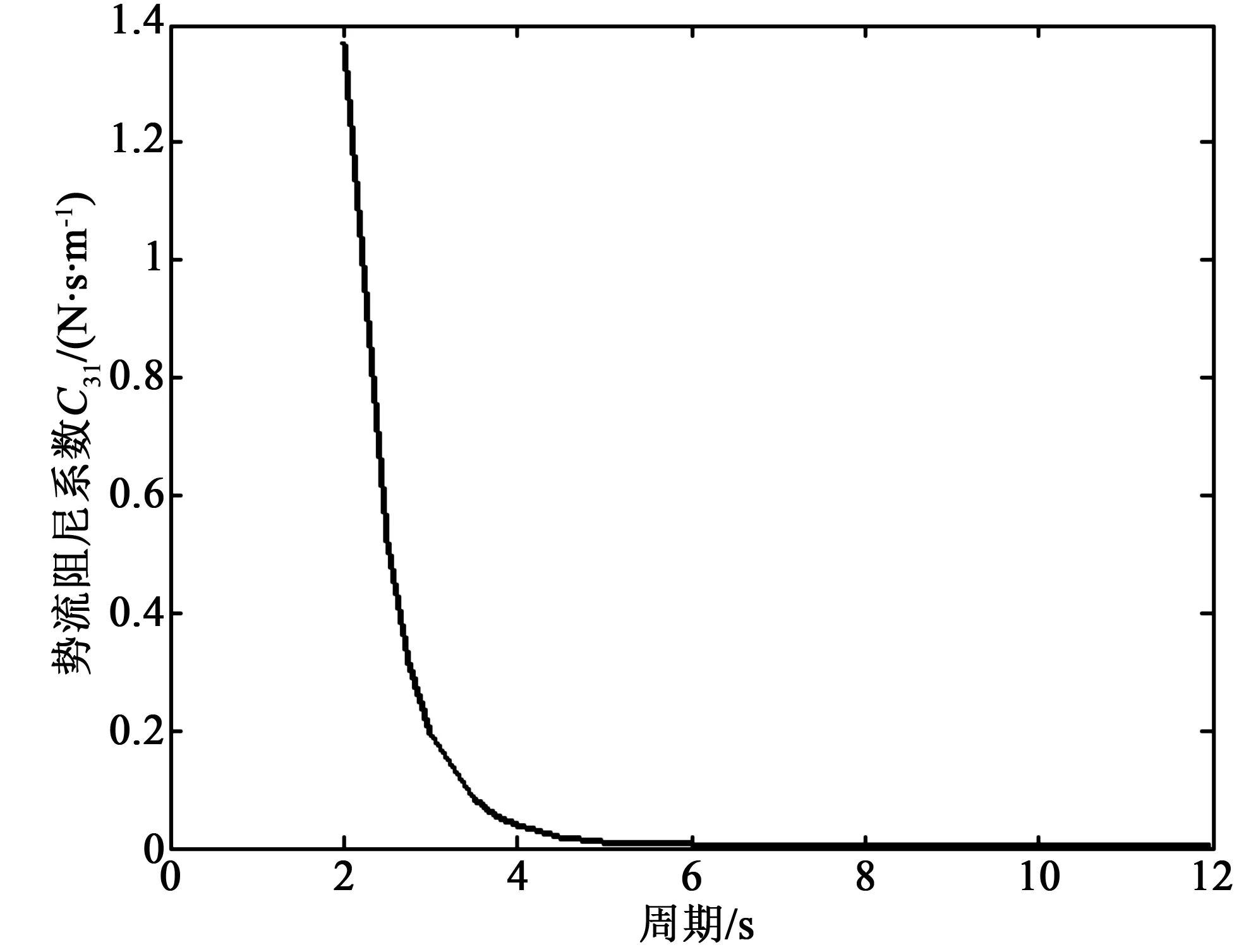
图10 3 m浮标垂荡-纵荡耦合自由度势流阻尼系数Fig.10 Coupled heave-surge potential damping coefficients of the 3 m diameter buoy

由图3～8可知，在常见波浪周期范围内，垂荡自由度的附加质量和垂荡波浪力随着入射波浪周期的增大而增大，而垂荡势流阻尼系数则随着周期的增大逐渐减小，10 m浮标和3 m浮标具有相同的变化趋势。相同波浪入射频率下，10 m浮标的附加质量、势流阻尼系数和波浪力计算值比3 m浮标大很多。

由图9～10可知，对称圆盘浮标结构的垂荡-纵荡耦合自由度的附加质量和阻尼系数均近似为零，计算结果与文献[13]的论述一致。所以，浮标的垂荡运动响应可由单自由度垂荡运动模型计算求解。

2.3 锚系垂向弹性系数

浮标采用全锚链单点悬链线式系泊方式。浮标所处水深为15 m，由于水深较浅，在研究中忽略锚系惯性与阻尼对浮标运动的影响，重点考虑锚系垂向张力对浮标运动的影响。浮标系链点处的锚系竖向张力可分成静常部分和时变部分，静常张力值取决于浮标的静平衡位置、锚系配置及水深等参数，可由悬链线理论计算求解。本文研究中，锚链张力静常部分影响浮标垂荡响应的平均值，它对浮标水下形状的改变影响很小，对浮标频域水动力参数的影响可以忽略；锚系张力时变部分取决于浮标瞬时垂荡位移，可由锚链的垂向弹性刚度系数描述，它影响浮标在波浪作用下的垂荡响应幅值。表3是水深15 m时，10 m浮标和3 m浮标的锚链特性参数。

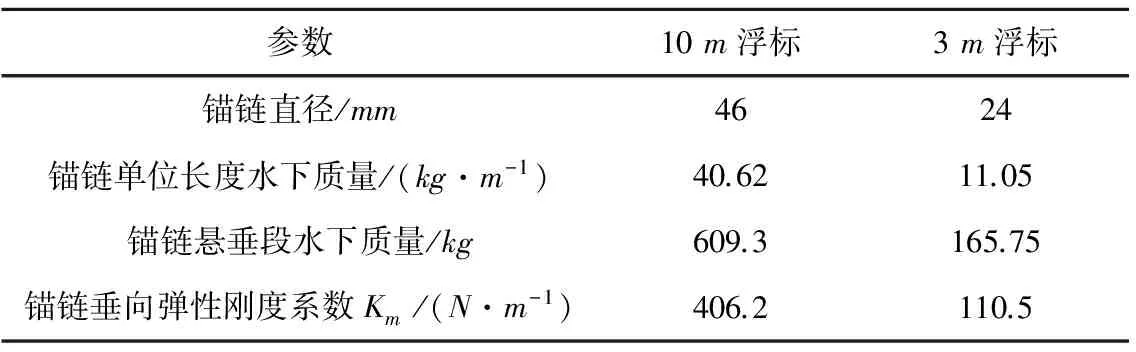
表3 浮标锚链特性

2.4 浮标垂荡运动响应

基于浮标水动力参数以及锚链垂向弹性系数计算结果，求解自由浮标以及系泊浮标的垂荡运动方程，获得不同入射波浪周期范围的浮标垂荡运动RAO。图11是10 m与3 m浮标在自由状态下的垂荡运动响应幅值算子，图12是10 m浮标在自由状态以及系泊状态下的垂荡运动响应幅值算子，图13是3 m浮标在自由状态以及系泊状态下的垂荡运动响应幅值算子。

图11 10 m和3 m浮标垂荡运动响应幅值算子 Fig.11 Heave RAO of the 10 m diameter and 3m diameter buoys

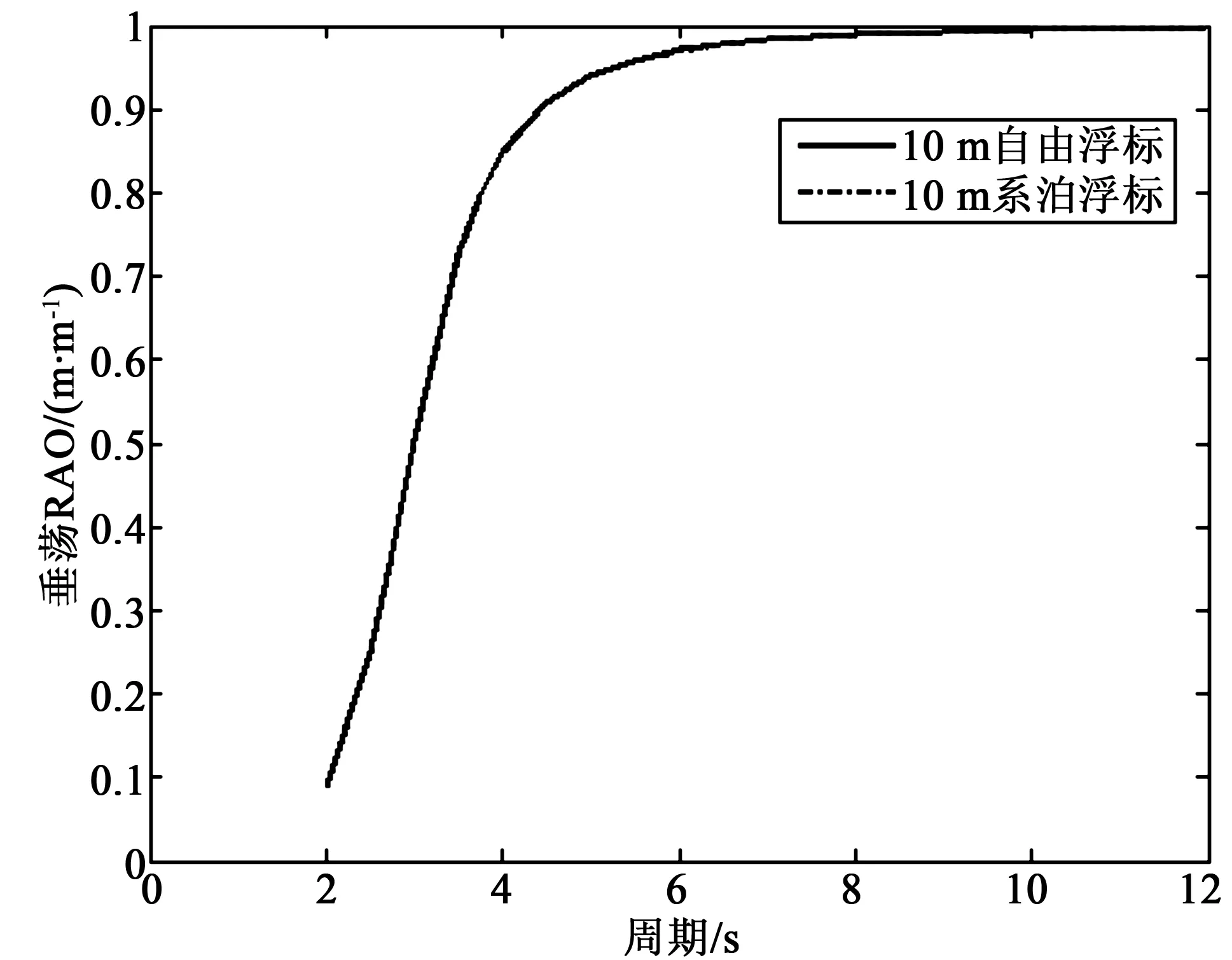
图12 10 m浮标垂荡响应幅值算子 Fig.12 Heave RAO of the 10m diameter buoy

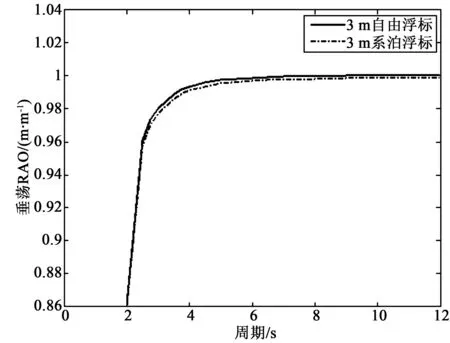
图13 3 m浮标垂荡响应幅值算子Fig.13Heave RAO of the 3 m diameter buoy

由图11可知，自由浮标的垂荡响应随着入射波浪周期的增大而增大，并逐渐趋向于1。10 m浮标在入射波浪周期为9 s时，垂荡响应幅值算子近似等于1，即浮标垂荡幅值等于入射波浪幅值；而3 m浮标在垂荡幅值等于波浪幅值时对应的起始波浪周期为6 s，说明3 m浮标的随波性能要优于10 m浮标。究其原因，在低周期波浪作用范围内，10 m浮标的附加质量和势流阻尼系数较3 m浮标增加的倍数要大于垂荡激励力增加的倍数，因此根据频域运动方程，同周期波浪作用下，10 m的垂荡响应幅值要小于3 m浮标。同时从垂荡运动响应幅值算子曲线上可知，浮标在其垂荡固有周期附近范围内并未发生共振，这是由于浮标在该波浪周期附近的势流阻尼系数较大，避免了共振现象的发生。

由图12和图13可知，锚系对10 m浮标的垂荡运动没有明显影响，而3 m浮标在考虑锚系作用前后，虽然运动趋势没有变化，但是垂荡响应幅值变小，这说明锚系对3 m浮标的垂荡运动影响要更为明显。

3 结论

本文在频域范围内研究了直径10 m和3 m浮标的垂荡运动响应特征，基于势流理论求解浮标的水动力参数，建立并求解单自由度垂荡运动方程，计算了自由浮标的垂荡运动；考虑系泊锚链垂向弹性系数的影响，探讨了系泊浮标的垂荡运动性能，并与自由浮标的垂荡运动进行了分析比较，得到以下结论：

(1)对于圆盘结构的海洋资料浮标，其他自由度的运动对垂荡运动没有耦合影响，单自由度垂荡分析模型即可准确描述浮标的垂荡运动响应。

(2)浮标的垂荡运动响应随着入射波浪周期的增大而增大，在常见波浪周期范围内没有发生共振现象。这是由于浮标垂荡运动周期较小，而势流阻尼在低周期时很大，从而避免了共振的出现。

(3)3 m浮标较10 m浮标具有更好的随波性。3 m浮标垂荡运动响应幅值算子小于1时对应的入射波浪周期范围为2～6 s，而10 m浮标所对应的入射波浪周期范围为2～9 s，在上述入射波浪周期范围内需要进行波浪传感器的参数修正。

(4)10 m浮标的锚系对浮标垂荡运动响应没有明显影响，可以不予考虑；而3 m浮标锚系使得浮标垂荡运动幅值减小，在计算中锚系的影响需要计入考虑。

本文在频域研究了浅水系泊浮标的垂荡运动响应，计算方法快捷高效，能够满足工程应用需求。但是，在研究中忽略了锚系的惯性力和阻尼力，因此本文的研究方法仅适用于近海资料浮标，对于深海资料浮标垂荡运动特性分析，则需要考虑锚系与浮标之间的耦合影响，以确定准确的浮标运动响应和锚系受力。

[1]BUNNIK T H J, de BOER G, COZIJN J L,et al. Coupled mooring analysis in large scale model test on a deepwater CALM buoy in mild wave conditions [EB/OL]. [2016-03-12]. http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx articleid=1575830.

[2]COZIJN J L, BUNNIK T H J. Coupled mooring analysis for a deep water CALM buoy[EB/OL]. [2016-03-12]. http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx articleid=1629260.

[3]COZIJN H， UITTENBOGAARD R, BRAKE E. Heave, roll and pitch damping of a deepwater CALM buoy with a skirt[EB/OL]. [2016-03-12].https://www.onepetro.org/conference-paper/ISOPE-I-05-296.

[4]UMAR A, DATTA T K .Nonlinear response of a moored buoy [J].Ocean Engineering, 2003,30 (13): 1625-1646.

[5]IDRIS K, LEONARD J W , YIM S C S. Coupled dynamics of tethered buoy systems [J]. Ocean Engineering, 1997, 24(5): 445-464.

[6]LEONARD J W, IDRIS K, YIM S C S. Large angular motions of tethered surface buoys [J]. Ocean Engineering, 2000,27 (12): 1345-1371.

[7]陈小红, 黄祥鹿. 单点系泊海洋资料浮标的动力分析[J].中国造船,1995(3):1-8.

[8]缪泉明, 顾民, 杨占明, 等. 极限海况下浮标运动及锚链受力估算[J]. 船舶力学, 2003, 7( 5) :21-27．

[9]范秀涛, 邵萌, 孙金伟, 等. 大型海洋资料浮标的运动性能研究[J]. 海洋技术学报, 2014，33(1):29-32.

[10]张继明, 范秀涛, 赵强，等.频域内海洋资料浮标水动力特性的仿真研究[J]. 山东科学, 2015, 28(4):8-13.

[11]COLBY C, SØDAHL N, KATLA E,et al. Coupling effects for a deepwater Spar[EB/OL].[2016-03-12].https://www.onepetro.org/conference-paper/OTC-12083-MS.

[12]戴遗山, 段文洋. 船舶在波浪中运动的势流理论[M].北京:国防工业出版社,2008.

[13]FALTINSEN O M. 船舶与海洋工程环境载荷[M].上海：上海交通大学出版社,2013.

Heave motion performance of ocean data buoy in frequency domain

WANG Hua-jie1, SUN Jin-wei1,2*, SHAO Meng2, FAN Xiu-tao1

(1. Shandong Provincial Key Laboratory of Ocean Environmental Monitoring Technology, Institute of Oceanographic Instrum entation, Shandong Academy of Sciences, Qingdao 266001, China; 2. Shandong Provincial Key Laboratory of Ocean Engi neering, School of Engineering, Ocean University of China, Qingdao 266100, China)

∶ As an important design parameter of ocean data buoy, wave following characteristic affects the accuracy of wave measurement. We calculate wave excitation force and such hydrodynamic coefficients as added mass and wave damping coefficient of disc buoy with three- dimensional potential flow theory, and heave motion of free floating buoy based on single degree of freedom motion equation. We also address heave motion of two moored buoys integrated with the impact of mooring vertical spring constant on buoy heave motion. We discover that the buoy with three-meter diameter has better wave following performance than that with ten-meter diameter and that anchor chain has more significant impact on heave amplitude of three-meter diameter buoy than that of ten-meter diameter buoy. The result is very important for parameter correction of wave sensors.

∶ocean data buoy; heave motion response; spring constant; frequency domain

10.3976/j.issn.1002-4026.2016.06.001

2016-07-19

山东省自然科学基金(ZR2015PE019)；中央高校基本科研业务费专项(201513056)；海洋公益性行业科研专项(201305028-3)；山东省自然科学基金(ZR2013DL007)；青岛市应用基础研究计划(14-2-4-66-jch)

王华洁(1976—)，女，研究方向为海洋仪器。Email:qdwanghj@sina.com

*通信作者，孙金伟，助理研究员，研究方向为海洋浮式结构水动力学及新能源利用技术。E-mail:chbhy03@163.com

TU311.3

A

1002-4026(2016)06-001-08