考虑疲劳折损的架空输电线路风雨荷载失效概率模型

何迪，章禹，郭创新，杨攀，金宇

(1.浙江大学电气工程学院，杭州市310027；2.贵阳供电局，贵阳市550002)

考虑疲劳折损的架空输电线路风雨荷载失效概率模型

何迪1，章禹1，郭创新1，杨攀2，金宇2

(1.浙江大学电气工程学院，杭州市310027；2.贵阳供电局，贵阳市550002)

作为典型的风振敏感结构，架空输电线路极易受强风雨灾害影响导致故障停运。为了研究强风雨天气及设备自身机械强度对线路失效概率的影响，从输电线路设计规范和材料结构性疲劳过程入手，建立了一种考虑疲劳折损的架空输电线路风雨荷载失效概率模型。模型采用非线性退化过程模拟材料疲劳折损，并依据荷载-强度干涉理论进行失效概率计算。算例分析给出了风、雨、疲劳折损三者作用时的线路失效概率情况，并以IEEE-RTS 79系统为例介绍了以本模型结果为基础筛选重要线路、薄弱档号的方法。该模型能量化不同风雨荷载对失效概率的增大作用，同时响应线路日常振动导致的疲劳折损，是一种全新的建模思路，具有较好的应用前景。

架空输电线路；失效概率模型；疲劳折损；风雨荷载

0 引 言

架空输电线路是电力系统中的重要生命线工程[1]。作为一种典型的风振敏感结构，架空输电线路杆塔高，跨度大，所处环境复杂多变，极易受极端强风雨灾害天气影响。尤其在东南沿海地区，季节性台风、大风引起的输电线路故障给电力系统的稳定运行造成了极大危害[2-3]。

强风雨灾害发生时架空输电线路发生故障的根本原因是作用于杆塔、线条和绝缘子串上的风雨荷载超过了设备个体可承受的机械强度，从而引起倒塔、断线等严重后果。实测与理论计算均表明：线条承受的风荷载相比塔体和绝缘子串承受的风荷载要明显大得多[1,4]，因此在输电线路抗风设计中线条风荷载的设计至关重要。国内外应用较为广泛的输电线路设计规范主要有：我国规范《110—750 kV 架空输电线路设计规范》(GB 50545—2010)[5]以及国际规范IEC 60826:2003[6]，美国规范ASCE No. 74[7]，欧盟规范EN50341-1:2001[8]等。

此外，在长期环境荷载作用下，架空输电线路时刻处于振动状态[9-11]。长期振动会导致股线内部抗拉力和线条静态力学性能的退化，进一步加剧了架空输电线路的断股、断线风险。

国内外学者针对架空输电线路的失效概率进行了大量研究，但基本都是采用基于回归模型、贝叶斯模型等的历史数据统计模型[12-13]或是从线路自身参数和实时天气状况出发建立的时变停运模型[14]，均未具体考虑强风雨及设备本身机械强度对线路可靠性的影响。部分文献介绍了风雨荷载下的输电线动力响应[9]，架空线路导线的疲劳过程[11,15]以及采用荷载-强度干涉理论建立的具体天气状况下的线路可靠度模型[16]，为本文模型的建立提供了借鉴思路。

为了研究强风雨天气以及设备自身机械强度对线路失效概率的影响，本文将建立考虑疲劳折损的架空输电线路风雨荷载失效概率模型，在风雨荷载模型和疲劳折损模型的基础上通过荷载-强度干涉理论对失效概率进行建模。最后，通过算例，分析风荷载、雨荷载以及线路疲劳折损三者分别或者共同作用时的线路失效概率情况，并基于失效概率模型进行重要线路、线路薄弱档号筛选，以验证模型的有效性。

1 风雨荷载模型

1.1 实际风荷载

根据GB 50545—2010[5]可知，线条风荷载Wx1及非标准高度z处的风速vz为：

(1)

vz=v0(z/z0)γ

(2)

式中:α为风压不均匀系数；μz为风压高度变化系数；μsc为线条风载体型系数；βc为线条风载调整系数；B为覆冰时风荷载增大系数，5 mm冰区取1.1，10 mm冰区取1.2；d为导线外径；Lp为杆塔水平档距；ρ0为该地该时刻的空气密度，一般可按常温常压取1.25 kg/m3；V0为基准高度为10 m的风速，m/s；θ为风向与导线轴向间的夹角；V0sinθ为实际作用风速。其中，α、μz、μsc、βc均可根据线条相关材料参数查阅GB 50545—2010获取。式(2)中，z、vz分别为计算高度及相应风速；z0、v0分别为标准高度及相应风速；γ为地貌分类参量，GB 50545—2010规定A、B、C、D 4类地貌的指数率分布参量γ分别为0.12，0.16，0.22，0.30。

联立式(1)及式(2)，则有：

(3)

1.2 实际雨荷载

强风天气一般伴随着降雨，需考虑雨荷载对风荷载的附加作用。一般认为雨滴谱服从马歇尔-帕尔默(Marshall-Palmer)指数分布[17-18]：

n(d′)=n0exp(-4.1I-0.21d′)

(4)

式中：d′为雨滴直径；n0为单位尺度单位体积内的雨滴个数基准值，8×103个/(m3·mm)；I为瞬时雨强，mm/h。

假设雨滴直径相同，结合雨滴冲击力模型[18]可计算相应雨荷载：

(5)

(6)

实际应用中，若风雨共同作用，V′可分解为竖直向速度Vy与顺风向速度Vx2部分。其中，Vy取雨滴在无风情况下的自由下落速度，Vx取顺风风速[18]，则顺风向雨荷载为

(7)

1.3 实际风雨荷载

联立式(3)和式(6)可计算雨荷载与风荷载的比值φ：

(8)

Wx=Wx1+Wx2x

(9)

本模型在风荷载基础上考虑雨荷载的目的一是为了使风雨荷载模型更精确，二是为了量化分析雨荷载对失效概率的影响。因此为了便于分析，可规定实际风雨荷载按照以下原则进行组合。

(1)风荷载为主要荷载，雨荷载为附加荷载，不考虑雨荷载单独作用造成架空线路故障的情况。

(2)根据雨荷载的作用机理，可以假定降雨过程中雨滴个体对结构的作用力是均匀的[18]，同时雨荷载本身相对于风荷载是附加荷载，其脉动分量可忽略不计。

(3)根据实际风速情况，工程上常把风速分解为周期大于10 min的平均风速和周期仅为几s的脉动风速2部分[19]。由于脉动风速的测量十分困难，为了降低测量误差对计算结果的影响，采用风速的概率分布来代替确切的风速值。包括GB 50545—2010在内的众多设计规范[5-8]均认为风速的概率分布为极值I型分布。根据极值分布的定义，风速的平方也服从极值I型分布，因此风雨荷载概率分布函数为

F(wx)=exp{-exp[-κ(wx-μx)]}

(10)

式中：wx为实际承受风雨荷载；μx为实际承受风雨荷载分布众值对应实际风雨荷载的计算值；κ为实际风雨荷载分布的尺度函数。

1.4 设计风雨荷载

同线路实际承受的风雨荷载一样，线路设计荷载也是一个非负的随机变量。IEC规程[6]认为线路设计荷载服从正态分布，并定义了线路设计荷载的变差系数Z为

Z=σ/μ

(11)

式中：σ为线路设计荷载的标准差；μ为线路设计荷载的均值，变差系数一般取0.05～0.2。

GB 50545—2010等设计规程在线路设计时均未考虑雨荷载，因此本文的设计风雨荷载实际为设计风荷载，在数值上等于设计风速下的荷载与设计活荷载分项系数以及结构重要性系数三者的乘积，其概率密度函数为

(12)

式中：wd为实际设计荷载；μd为线路设计荷载均值；σd为设计荷载标准差。

2 疲劳折损模型

架空输电线路架设于野外，常年经受风雨等自然环境的侵害。当风速为0.5～10 m/s的风作用于导线时，导线背风侧会形成交替卡门(Karman)漩涡[20]，进而产生交变应力，引起导线振动。长期微风振动极易造成导线的疲劳破坏，引发股线内部抗拉力和线条静态力学性能的退化[15]。材料的疲劳折损过程可采用非线性强度退化模型[21]进行描述：

(13)

式中：n为循环次数；s为应力水平；N为总寿命次数；σ0为材料初始静拉伸断裂强度；σ为材料剩余强度；p、q为材料常数。

式(13)的离散积分式为

(14)

式中：si、ni分别表示等值应力和等值循环次数；σ(ni-1)、σ(ni)表示应力作用前后材料的剩余强度。

若应力保持不变，则材料到达寿命终点时，有：

(15)

正常状况下，应力水平s远小于初始静拉伸断裂强度σ0，式(15)可近似写为：

(16)

(17)

Wöhler根据累计损伤理论进行了导线的疲劳试验，总结了导线表面应力水平s与最大振动次数N的关系，即Wöhler安全边界曲线[22]。钢芯铝绞线属于多层铝股，其安全边界曲线为

(18)

联立式(17)、(18)即可求取退化模型的p、q值，即：

(19)

根据式(14)可知k次应力循环前后线条的静拉伸断裂强度函数关系为

(20)

式中：等值应力si可采用在线监测技术[10]采集的数据进行计算后获取，详见附录A；等值循环次数ni可根据IEEE疲劳试验法推理获得，详见附录A。

正常情况下，输电线路处于微振状态，应力水平s≤15.6N/mm2，此时式(19)中的p、q值可设为基准材料常数p0、q0，则式(20)可变为

(21)

(22)

式中kde为退化率，kde=Dde/D0。Dde可通过记录每个时段Tj内退化量Ddej累加获得，详见附录A。

变差系数作为线路既定常数[6]，若其在疲劳过程中不随时间的变化而改变，则设计风雨荷载的概率密度函数为

(23)

3 考虑疲劳折损的风雨荷载失效概率模型

只考虑可靠与失效两状态分布时，可认为实际承受的风雨荷载小于设计风雨荷载时，线路可靠。因此，依据荷载-强度干涉理论，可进行风雨荷载下线路失效概率的计算。图1为荷载-强度干涉图。

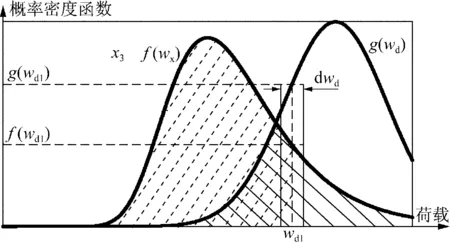
图1 荷载-强度干涉图Fig.1 Interferogram of load-strength

如图1所示，设wx、wd分别表示架空输电线路实际承受的风雨荷载和设计可承受风雨荷载的随机变量，则两者的概率密度函数f(wx)、g(wd)是2个独立的随机变量函数，两概率密度函数重叠形成的干涉区(图1中实线阴影区域)则表示线路有发生故障的可能。需要注意的是，干涉区面积并不等于线路故障失效的概率。取一足够小的区间dwd，其中点为wd1，则设计风雨荷载落入该区间的概率为该区域的面积，即

(24)

而实际承受的风雨荷载小于wd1的概率为

(25)

则在区间dwd内某档线路可靠的概率等同于图1中虚线阴影区域的面积，其值为

(26)

式中wx、wd均能取到所有非负值，则该档线路可靠的概率为

(27)

式中F(wd)、g(wd)可由式(10)、(23)分别计算获得。

若某条线路可根据档距分为n档，则该条线路可靠的概率为

(28)

相应地，线路失效的概率Pf以及第i档线路对整条线路失效概率的贡献度Coni为：

Pf=1-Pr

(29)

Coni=(1-Pi)/Pf

(30)

需要注意的是，由于wx、wd均是Lp(z/z0)2γ的线性函数，线路的失效概率Pr与线条的高度、档距均无关。

4 算例分析

4.1 算例简介

本模型算例中的架空输电线路采用常见的线型为LGJ—300/40的110 kV导线，导线外径为23.94 mm，线条均高为30 m，水平档距值为500 m，无覆冰，B形地貌，雨滴历史统计直径区间为[0.1,0.5]mm，线路设计风速Vde为27 m/s，实际风速V根据风速测量仪测量值或者接入气象部门数据获取。设计风荷载的变差系数为0.07，设计活荷载分项系数为1.4，材料重要度系数为1，风雨荷载尺度系数统计值为0.091。

4.2 理论分析

图2给出了无疲劳折损线路不同降水下瞬时作用风速V0sinθ与失效概率的对应曲线以及不同瞬时作用风速下瞬时雨强I与失效概率的对应曲线。可见，随着瞬时雨强的增加，架空输电线路失效概率上升，但其上升的幅度缓慢，远不及作用风速的增大引起的失效概率增大的幅度。结果验证了风荷载是主要荷载，雨荷载为附加荷载的模型假设。如果单位时间风速和降水量均较小，在实际失效概率计算中甚至可以忽略雨荷载的作用。

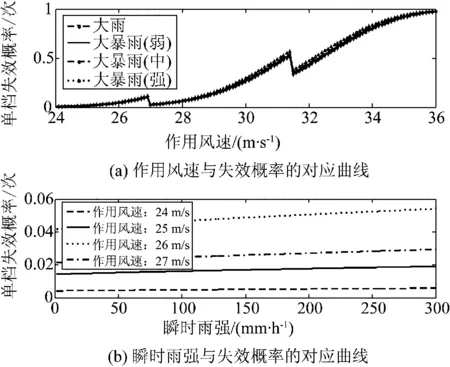
图2 作用风速、瞬时雨强与失效概率的对应曲线Fig.2 Corresponding curves of wind function velocity, instantaneous precipitation and failure probability

此外，图2中在风速为27 m/s和31.5 m/s处有2个失效概率突降点，其原因是GB 50545—2010在定义风压不均匀系数α时的跳跃导致了临界风速时高风速下的风荷载甚至小于低风速下的风荷载。尽管输电线路实际运行经验表明目前GB 50545—2010规程参数取值在工程应用意义上有一定合理性和实用性，本文模型的提出仍对其中参数的精度提出了研究意义上的更高要求。

通过模拟一段时间内导线微风振动数据可得到该时间段内日强度退化量Ddej、剩余强度量Dr及疲劳折损系数ξ的变化情况，如图3所示。结合图4可见，随着服役时间的增长以及微振导致的退化量的累积，线路在相同风雨荷载下的失效概率有所增加。此外，随着退化量的累积，疲劳折损对失效概率的影响越发显著。在不考虑线路投运初期由于制造缺陷、安装不当等引起的早期偶然故障的情况下，模型十分契合浴盆曲线老化期的变化趋势。由于服役中线路的股线内部抗拉力和线条静态力学性能的测量十分困难，通过测量并记录线条的退化率kde及总退化量Dde是一种能较好反应线路疲劳折损程度的方法，能为线路的视情维修及更换操作提供理论和技术支持。

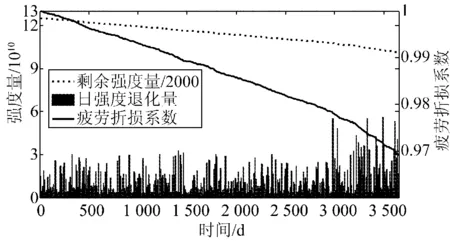
图3 模拟疲劳折损过程Fig.3 Fatigue impairment process simulation

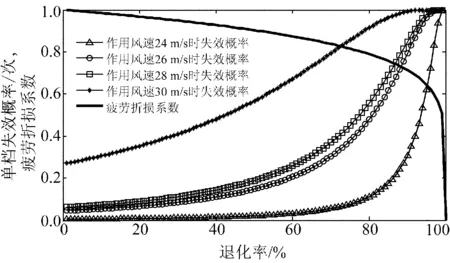
图4 疲劳折损与失效概率的对应曲线Fig.4 Corresponding curve of fatigue impairment and failure probability

4.3 实例应用

图5为某次强风雨过境时某气象监测装置测量到的瞬时风速V0、瞬时作用风速V0sinθ与瞬时雨强I信息。

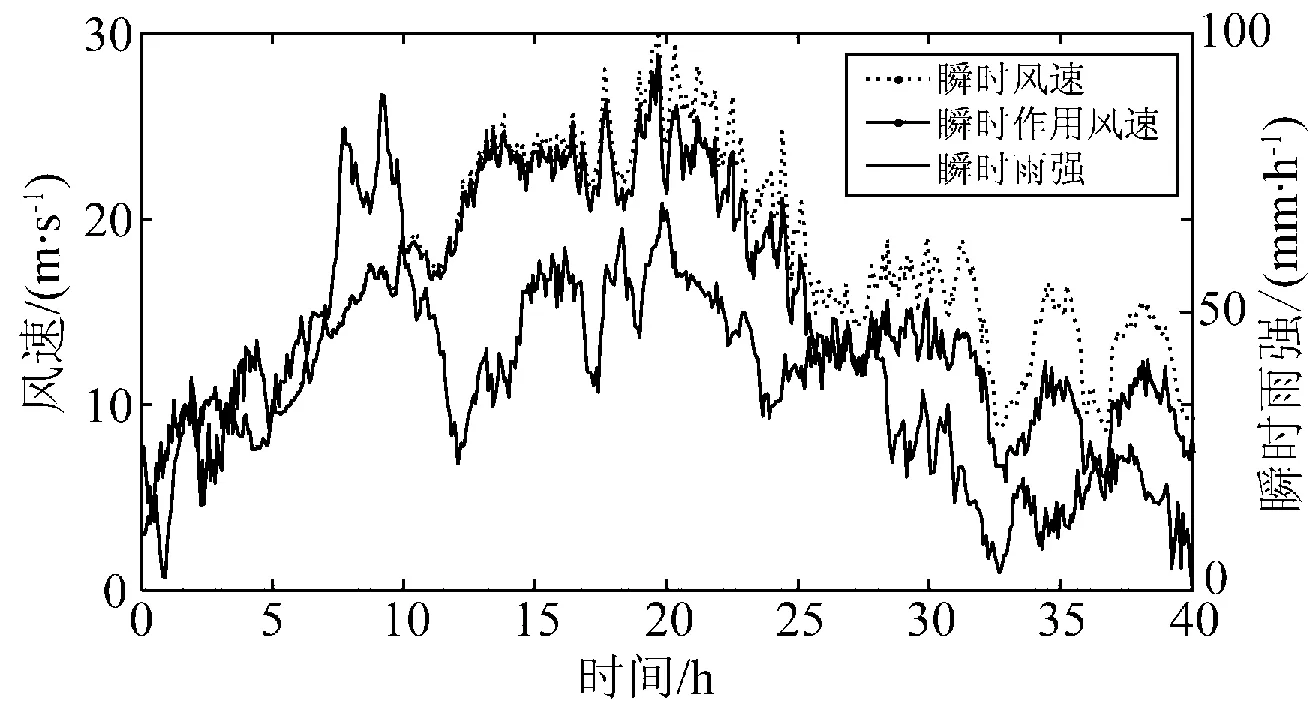
图5 某次强风雨过境时风速与瞬时雨强信息Fig.5 Information of wind velocity and instantaneous precipitation in a certain storm

将气象监测信息作为失效概率模型的输入，可计算在强风雨过境时相应各档线路及整条线路的失效概率实时变化情况，如图6所示。由图6可知，20 h左右该档线路失效概率最大，达到了单档0.119 1次。表1为该时刻不同瞬时雨强、不同线路退化率对该档线路失效概率的影响情况。由表1可见，疲劳折损使线路抗风雨能力明显降低。此外，当风速足够大时，雨荷载对失效概率的贡献是不可忽视的。

根据不同线路个体在强风雨荷载下的失效概率，可通过风险追踪方法[23]量化风雨灾害下各线路的重要程度，遴选系统重要线路及线路重要档号。

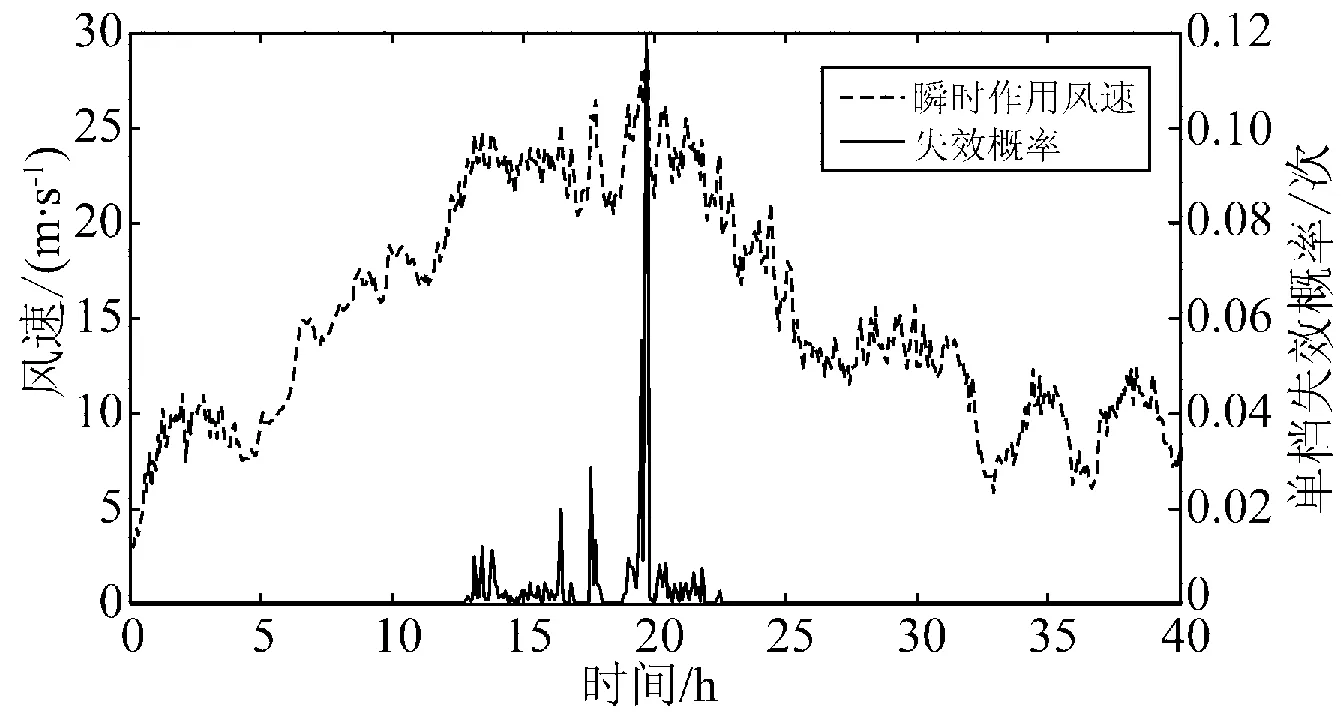
图6 强风雨过境时某档号线路的失效概率Fig.6 Failure probability of a certain span in a storm

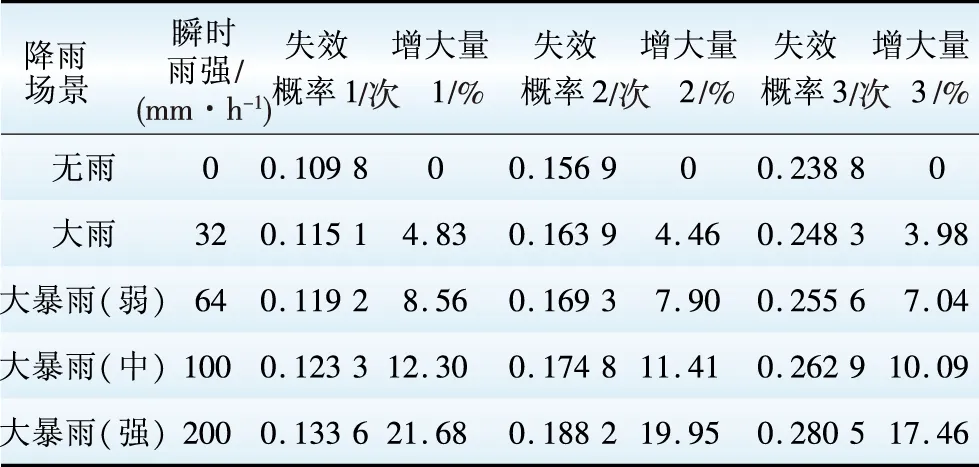
注：1—无折损线路；2—退化率kde为20%的线路；3—退化率kde为40%的线路。

根据不同的应用场景，选取不同方式对线路重要度、失效概率和各档失效概率贡献度等指标进行组合，结合应急资源、应急人员布置情况、电网运行工况等信息进行线路失效风险分析、连锁故障风险分析[26]及系统风险评估[27]，可为强风雨灾害下的电网应急调度和优化决策提供技术支持。

表2 线路重要度及各档失效概率贡献度分析结果
Table 2 Analysis results of importance and failure probability contribution of span for lines

5 结 论

通过算例分析可知，本文建立的考虑疲劳折损的架空输电线路风雨荷载失效概率模型具有以下优点。

(1)模型综合考虑强风雨天气和设备因自身老化引起的结构性疲劳对失效概率的影响，从设备实际应力荷载出发以荷载-强度干涉理论对失效概率进行建模，精度较高，能充分反映设备的实际情况和个体间差异性，为挖掘强风雨灾害下线路的薄弱环节提供理论支持。

(2)风荷载建模严格遵循我国输电线路设计规范GB 50545—2010，并根据风荷载建模规则对雨荷载进行建模量化，之后以一定规则对风雨荷载进行组合，荷载模型相对严谨，可靠性较高。

(3)从振动机理出发，根据非线性强度退化过程对线路疲劳折损进行建模，能充分响应由于日常振动导致的导线疲劳退化过程。

由于模型的精度取决于风速、风向的测量精度，因此下一步的工作重点将是通过大数据处理分析技术清洗、挖掘出高精度的测量数值以减小风雨荷载失效概率的计算偏差。

[1]汪大海，吴海洋，梁枢果．输电线风荷载规范方法的理论解析和计算比较研究[J]．中国电机工程学报，2014，34(36)：6613-6621． WANG Dahai，WU Haiyang，LIANG Shuguo. Theoretical analysis and comparison on typical international wind load codes of transmission conductors [J]．Proceedings of the CSEE，2014，34(36)：6613-6621．

[2]吴勇军，薛禹胜，谢云云，等．台风及暴雨对电网故障率的时空影响[J]．电力系统自动化，2016，40(2)：20-29． WU Yongjun，XUE Yusheng，XIE Yunyun，et al．Space-time impact of typhoon and rainstorm on power grid fault probability[J]．Automation of Electric Power Systems，2016，40(2)：20-29．

[3]吴明祥，包建强，叶尹，等．超强台风“桑美”引起温州电网输电线路事故的分析[J]．电力建设，2007，28(9)：39-41． WU Mingxiang，BAO Jianqiang，YE Yin，et al. Transmission line accident analysis of Wenzhou grid caused by super typhoon “SAOMAI”[J]．Electric Power Construction，2007，28(9)：39-41．

[4]MOMOMURA Y，MARUKAWA H．Full-scale measurements of wind-induced vibration of a transmission line system in a mountainous area[J]．Journal of Wind Engineering and Industrial Aerodynamics，1997(72)：241-252．

[5]住房与城乡建设部．110 kV～750 kV 架空输电线路设计规范：GB 50545—2010 [S]．北京：中国计划出版社，2010．

[6]International Electro-technical Commission．Design criteria of overhead transmission lines：IEC 60826 2003 [S]．IEC，2003．

[7]American Society of Civil Engineers．Guidelines for electrical transmission line structural loading：ASCE: No．74 [S]．USA： ASCE，2009．

[8]SFS-EN．Overhead electrical lines exceeding AC 45 kV Part 1：general requirements. Common Specifications：EN 50341-1 [S]．SFS-EN，2001．

[9]白海峰，李宏男．架空输电线风雨致振动响应研究[J]．电网技术，2009，33(2)：36-40． BAI Haifeng，LI Hongnan．Dynamic response of overhead transmission lines to oscillation caused by wind or rainfall loads[J]．Power System Technology，2009，33(2)：36-40．

[10]黄新波，赵隆，舒佳，等．输电线路导线微风振动在线监测技术[J]．高电压技术，2012，38(8)：1863-1865． HUANG Xinbo，ZHAO Long，SHU Jia，et al．Online monitoring conductor aeolian vibration of transmission lines[J]．High Voltage Engineering，2012，38(8)：1863-1865．

[11]孔德怡，李黎，龙晓鸿，等．输电线微风振动疲劳寿命影响因素分析[J]．武汉理工大学学报，2010，32(10)：53-57． KONG Deyi，LI Li，LONG Xiaohong，et al．Parametric investigation on fatigue life of transmission line subjected to aeolian vibration[J]．Journal of Wuhan University of Technology，2010，32(10)：53-57．

[12]LIU H，DAVIDSON R A，APANASOVICH T V．Spatial generalized linear mixed models of electric power outages due to hurricanes and ice storms[J]．Reliability Engineering and System Safety，2008，93(6)：897 -912．

[13]ZHOU Y，PAHWA A，YANG S．Modeling weather-related failures of overhead distribution lines[J]．IEEE Transactions on Power System，2006，21(4)：1683-1690．

[14]何剑，程林，孙元章，等．条件相依的输变电设备短期可靠性模型[J]．中国电机工程学报，2009,29 (7)：39-46． HE Jian，CHENG Lin，SUN Yuanzhang，et al．Condition dependent short-term reliability models of transmission equipment[J]．Proceedings of the CSEE，2009,29，29(7)：39-46．

[15]王洪，柳亦兵，董玉明，等．架空线路导线疲劳试验振动幅度的研究[J]．中国电机工程学报，2008，28(4)：123-128． WANG Hong，LIU Yibing，DONG Yuming，et al．The study of conductor fatigue test amplitude of overhead lines[J]．Proceedings of the CSEE，2008，28(4)：123-128．

[16]孙羽，王秀丽，王建学，等．架空线路冰风荷载风险建模及模糊预测[J]．中国电机工程学报，2011，31(7)：21-28． SUN Yu，WANG Xiuli，WANG Jianxue，et al．Wind and ice loading risk model and fuzzy forecast for overhead transmission lines[J]．Proceedings of the CSEE，2011，31(7)：21-28．

[17]盛裴轩，毛节泰，李建国，等．大气物理学[M]．北京：北京大学出版社，2003．

[18]李宏男，任月明，白海峰．输电杆塔体系风雨激励的动力分析模型[J]．中国电机工程学报，2007，27(30)：43-48. LI Hongnan，REN Yueming, BAI Haifeng．Rain-wind induced dynamic model for transmission tower system[J]．Proceedings of the CSEE，2007，27(30)：43-48．

[19]IANNUZZI A，SPINELLI P．Artificial wind generation and structural response[J]．Journal of Structural Engineering ASCE，1987，113(10)：2382-2398．

[20]郑玉琪．架空输电线微风振动[M]．北京：水利出版社，1987．

[21]吕文阁，谢里阳，徐灏．一个非线性强度退化模型[J]．机械强度，1997，19(2)：55-57． LV Wenge，XIE Liyang，XU Hao．A nonlinear model of strength degradation[J]．Journal of Mechanical Strength，1997，19(2)：55-57．

[22]WOHLER B．Recommendations for the evaluation of the lifetime of transmission line conductors[R]. Sarajevo: CIGRE，1979．

[23]邓彬，郭创新，王越，等．基于well-being分析的电网设备重要度评估与排序方法[J]．电网技术，2013，37(12)：3489-3496． DENG Bin，GUO Chuangxin，WANG Yue，et al．An assessment and ranking method for component importance based on well-being analysis [J]．Power System Technology，2013，37(12)：3489-3496．

[24]SUBCOMMITTEE P M. IEEE reliability test system[J]. IEEE Transactions on Power Apparatus and Systems, 1979 (6): 2047-2054.

[25]PALO A．Transmission line reference book: wind induced conductor motion[M]．California，USA: Electric Power Research Institute，1979．

[26]许小兵，吴锡斌，徐培栋，等．考虑线路停运率的电网连锁故障风险评估[J]．电力建设，2013，34(8)：116-120． XU Xiaobing，WU Xibin，XU Peidong，et al．Risk assessment of cascading failure in power grid considering line outage rate[J]．Electric Power Construction，2013，34(8)：116-120．

[27]莫若慧，左俊军，龙裕芳，等．适合风雨气候的电力系统风险评估模型与方法[J]．电力建设，2015，36(2)：21-26． MO Ruohui，ZUO Junjun，LONG Yufang，et al．Risk assessment model and method of power system in storm climate[J]．Electric Power Construction，2015，36(2)：21-26．

(编辑 张小飞 )

附录A

(1)等值应力si的计算。美国电力科学研究院通过线夹出口处的弯曲振幅试验提出了导线动弯应力与微风振动振幅之间的关系[25]：

(A1)

(2)等值循环次数ni的计算。IEEE疲劳试验法给出了输电线路的振动频率fi与风速vi之间的联系[16]:

fi=Sstvi/D

(A2)

式中:Sst为斯特劳哈尔(Strouhal)数，一般可取185～210。

在一定时间段Tj内，输电线路的微风振动过程可认为是平稳高斯随机过程，一般可用威布尔分布来模拟平均风速概率分布[12]。将风速分为k个区间，根据卡门漩涡的锁定效应[21]，当风速在一定范围内变化时，导线的振动频率和漩涡的脱落频率均保持不变。则风速处于风速区间i的概率为

Pi(Vidown≤v≤Viup)=
exp[-(Vidown/η)β]-exp[-(Viup/η)β]

(A3)

式中:Vidown、Vidown分别表示区间风速上下限；β为形状参数;η为比例参数，可由实测风速风向数据求取。

因此风速区间i的振动总次数为

ni=fiti=SstviPiTj/D

(A4)

(3)路服役期间的总退化量Dde的计算。根据式(20)和附录A可知，Tj内的强度退化量Ddej为

(A5)

通过记录每个时间段Tj内的强度退化量，可以求解获得线路服役期间的总退化量Dde为

(A6)

附录B

RTS79系统[24]是IEEE Power Engineering Society开发的测试系统，基本年负荷峰值为2 850 MW。有24个节点，38条线路和32台发电机。系统单线图如附录图B所示。发电机组等级和可靠性数据、线路长度与强迫停运率数据、负荷数据均为默认值。以线路长度0.5英里为档距设立档号。

Wind and Rain Loading Failure Probability Model for Overhead Transmission Lines Considering Fatigue Impairment

HE Di1, ZHANG Yu1, GUO Chuangxin1, YANG Pan2, JIN Yu2

(1. College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China; 2. Guiyang Electric Power Supply Bureau, Guiyang 550002, China)

As typical wind-sensitive structures, overhead transmission lines are easily affected by extreme weather disasters which will cause failure outage. In order to study the impacts of strong storm and device mechanical strength on the line failure probability, this paper constructs a wind and rain load failure probability model with considering fatigue impairment based on the design code of transmission line and material structural fatigue process. The model adopts a nonlinear process of strength degradation to describe the material fatigue impairment and utilizes the interference theory of load-strength to calculate the failure probability. We demonstrate different circumstances of failure probability under wind, rain and fatigue impairment, and take IEEE-RTS79 system as example to introduce a screening method for important lines and weak spans based on this model. The model can not only quantitatively analyze the increase impact of different wind and rain loads on the failure probability, but also have response to the fatigue impairment caused by daily physical vibration of lines, which is a new modeling idea and has a good application prospect.

overhead transmission line; failure probability model; fatigue impairment; wind and rain load

图B1 IEEE-RTS79系统示意图Fig.B1 Diagram of IEEE-RTS79

国家高技术研究发展计划(863计划)(2015AA050204)；浙江省自然科学基金(LZ14E070001)

TM 753

A

1000-7229(2016)07-0133-08

10.3969/j.issn.1000-7229.2016.07.019

2016-01-25

何迪(1991)，男，硕士研究生，主要研究方向为输变电设备的状态监测、可载性分析和风险评估;

章禹(1993)，男，硕士研究生，主要研究方向为配网供电能力评估;

郭创新(1969)，男，博士，教授，博士生导师，主要研究方向为输变电设备状态检修、智能信息处理技术及其在电力系统中的应用；

杨攀(1982)，男，本科，主要研究方向为电网调度运行；

金宇(1986)，男，本科，主要研究方向为电网调度运行。

Project supported by National High Technology Research and Development Program of China (863 program) (2015AA050204)