供电无源网络的VSC-HVDC系统控制器及PI参数研究
李向阳,刘应梅,王明东
(1.郑州大学电气工程学院,郑州市 450001;2.中国电力科学研究院,北京市 100192)
供电无源网络的VSC-HVDC系统控制器及PI参数研究
李向阳1,刘应梅2,王明东1
(1.郑州大学电气工程学院,郑州市 450001;2.中国电力科学研究院,北京市 100192)
电压源型高压直流输电技术(voltage source converter based high voltage direct current transmission,VSC-HVDC)在无源网络供电领域具有较好的应用前景。首先分析了向无源网络供电的两端VSC-HVDC的系统结构和工作原理,建立了系统在d-q同步旋转轴下的欧拉-拉格朗日数学模型;其次设计了PI双闭环和无源双闭环2种控制器;再次提出了基于对称最优法的外环控制器参数整定方法;在PSCAD/EMTDC中搭建了向无源网络供电的两端VSC-HVDC仿真系统,分别采用PI双闭环和无源双闭环控制器,对无源网络负荷功率变化和电压下降2种工况进行了仿真分析。仿真结果表明:所提出的控制参数整定方法是正确有效的,设计的无源双闭环控制器和PI双闭环控制器都可以实现电压、电流的快速精准控制,使无源网络电压稳定在给定值,相对而言,无源双闭环控制器的动态控制性能更好。
电压源型高压直流输电技术(VSC-HVDC);无源网络;无源控制器;双闭环控制;PI参数整定
0 引 言
近几年发展起来的基于脉宽调制技术和绝缘栅双极型晶体管器件的电压源型高压直流输电技术(voltage source converter based high voltage direct current transmission,VSC-HVDC)不仅可以实现有功和无功功率独立解耦控制[1],还具有“黑启动”功能,对接入的交流系统没有特殊要求,克服了传统直流输电技术不能向无源网络供电的缺陷[2]。因此,VSC-HVDC输电技术在偏远地区供电、新能源并网和城市供电等方面具有较强的优势[3]。挪威的Troll-A VSC-HVDC工程[4]是世界上第1个利用柔性直流输电技术向海上钻井平台供电的商业化工程,它采用了ABB公司的两电平换流器拓扑,目前运行良好。
相幅控制[5]和直接电流控制是VSC的2种主要控制方法。直接电流控制[6]可以直接控制系统的响应电流,动作速度快,还能抑制某些故障情况下的短路电流,因此得到了广泛应用。针对使用VSC-HVDC向弱交流系统和无源网络供电的情况,国内外学者做了大量的研究,指出无源网络供电的可靠性关键在于使其交流电压和频率稳定。文献[7]对VSC-HVDC系统供电无源网络的调节特性进行了分析,指出无源逆变系统的频率不变性,同时在逆变侧应用相幅控制来稳定负荷电压。文献[8]建立了VSC-HVDC输电系统供电无源网络的物理实验系统,但是其无源侧电压控制器忽略了电流负反馈。
文献[9]中提出的直接电压控制本质上也是一种相幅控制。文献[10]设计了向无源网络供电的双闭环控制器,但没有对外环电压控制进行阐述。文献[11]结合负荷侧滤波器设计了PI双闭环控制器,但没有对PI参数的选取进行说明,控制参数不易确定。
本文基于VSC-HVDC系统向无源网络供电的工作原理和特点,建立系统在d-q同步旋转轴下的欧拉-拉格朗日数学模型,设计PI双闭环和无源双闭环2种控制器,并提出基于对称最优法的外环控制器参数整定方法。最后,在PSCAD/EMTDC仿真软件中建立向无源网络供电的两端VSC-HVDC仿真系统,对无源网络侧负荷功率变化和电压降低等工况进行仿真分析,并对提出的基于对称最优法的外环控制器参数整定方法进行验证,对设计的PI双闭环和无源双闭环控制器的性能进行比较分析。
1 VSC-HVDC系统结构和数学模型
1.1 两端VSC-HVDC系统结构
如图1所示,本文采用的两端VSC-HVDC系统由一个交流网络和无源负载经直流电缆连接组成。图1中,us1、us2为公共连接点PCC1和PCC2处的电压;uc1、uc2为2个换流站交流侧输出基波电压;E1、E2为换流站直流侧电压;i1、i2、iL分别为送端电流,受端电流和无源负荷电流;R1+jL1、R2+jL2分别为整流侧和逆变侧的等效电阻和电感。
1.2 VSC-HVDC系统数学模型
由于两端VSC-HVDC系统的2个换流站结构相同,本文以逆变站为例进行分析。在逆变站,换流器的交流侧通过换相电抗(R2+jL2)和并联电容器C向无源负载供电。其等效电路如图2所示。并联电容器C既有滤波[12]的功能又能向无源负载提供无功补偿[13]。

图1 两端VSC-HVDC系统结构图Fig.1 Structure of a two-terminal VSC-HVDC system
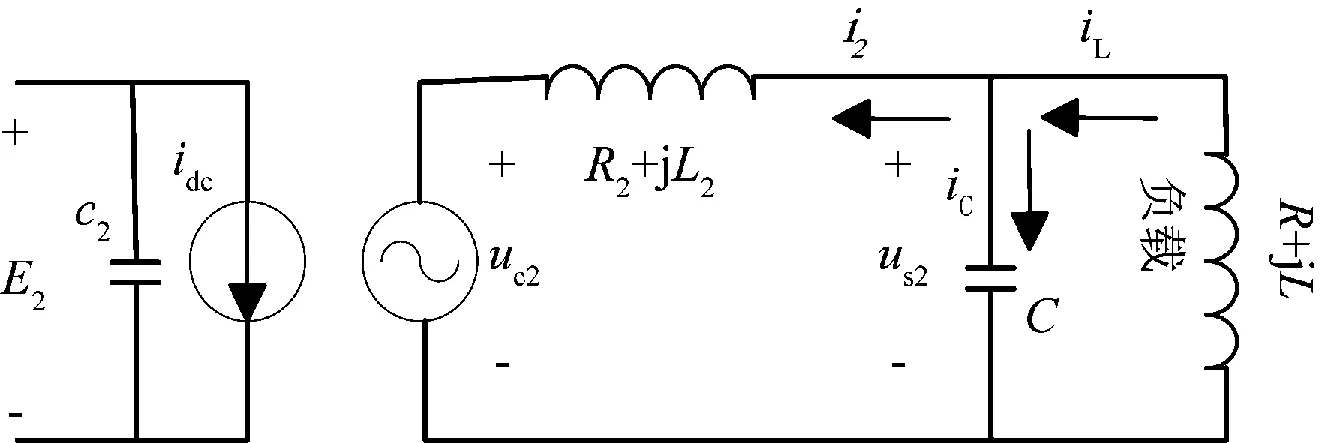
图2 逆变站等值电路Fig.2 Equivalent circuit of inverter station
稳态运行时,由基尔霍夫定律可得:
(1)
(2)
对式(1)进行Park变换,得到d-q同步旋转坐标系下的数学模型为
(3)
类似地,对式(2)进行Park变换得:
(4)
式(3)和式(4)中:us2d、us2q为负载电压的d-q轴分量;uc2d、uc2q为逆变站交流侧基波电压的d-q轴分量;i2d、i2q为逆变站交流电流的d-q轴分量;iLd、iLq为负荷侧电流的d-q轴分量。
当d轴定位在负载电压矢量上时,us2q=0,根据瞬时功率理论,有功和无功功率为
(5)
由式(5)知,只要分别控制i2d和i2q就可以实现有功和无功的解耦控制。
2 VSC-HVDC系统控制器设计
向无源网络供电的两端VSC-HVDC系统中,整流站作为功率平衡节点,通常采用定直流电压和定无功功率控制[8-9],在此不再详细阐述;逆变站的控制目标是保持无源网络交流电压幅值和频率的恒定,向负荷提供所需的功率。因此,逆变站需采用定交流电压和定频率控制。本文着重对逆变站的控制进行研究,外环电压采用PI控制器,分别与内环电流无源控制器和PI控制器级联构成负荷侧的无源双闭环控制器和PI双闭环控制器。
2.1 内环电流PI控制器
由式(3)知,内环电流PI控制器可以设计为:
(6)
(7)
式中:i2dref、i2qref是电流i2d、i2q的参考值,由外环控制器给出;PI1=PI2=kp1+ki1/s是内环控制器的比例、积分系数。通过调节换流阀的控制输入uc2d、uc2q,使状态变量i2d、i2q快速跟踪其参考值的变化,实现内环控制器的功能。考虑到换流站的开关频率较高[14],可以忽略换流器的延迟作用,则内环控制器的传递函数框图如图3所示。

图3 内环电流PI控制器Fig.3 Inner-loop current PI controller
2.2 内环电流无源控制器
将式(3)改写成矩阵形式有:
(8)
则VSC的EL方程为
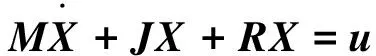
(9)
(10)
式中:M,J,R分别为正定对角阵,反对称矩阵和正定对称矩阵,其中J体现了状态变量X的互联特性,R体现了系统的耗散特性,控制输入u体现了系统的能量交换性。
对于VSC系统,设其能量存储函数为H= 0.5XTMX,由式(9)得:
(11)
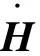
VSC稳态运行时,应使电流分量i2d、i2q稳定在电压外环控制输出的参考值i2dref、i2qref,即稳态平衡点为:X*=[i2drefi2qref]T。
(12)
为使系统加速收敛,需注入一定阻尼,使He迅速为0,设阻尼为Ra=diag[Ra1Ra2]。则式(12)可变为
(13)
取无源控制律为
(14)
则:
(15)
此时误差能量函数即为李亚普诺夫函数,故误差能量函数能迅速收敛,且收敛速度与Ra大小有关。将式(14)展开可得d-q轴无源控制律,见式(16),其控制器框图如图4所示。
(16)
2.3 外环电压控制器
由于逆变站连接的是无源网络,如何保证负载电压和频率的稳定是最关键的问题。无源网络没有发电设备,不能通过直接测量获得系统的同步相位,本文基于无源网络的频率不变性[7]以压控振荡器代替锁相环给定了电网频率。对于电压的控制,传统的方法忽略了电流负反馈,采用相幅控制[7-9]来解决这一问题。对负荷侧并联电容的电路分析可知,式(4)和换流器的d-q轴数学模型式(3)结构相似,故可根据式(4),采用类似于内环电流控制器的设计方法来实现外环电压控制。类比式(6)、(7),外环电压d-q轴PI控制器可以设计为:
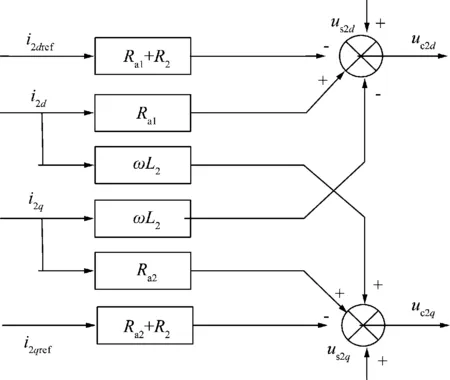
图4 内环电流无源控制器Fig.4 Inner-loop current passive controller
(17)
(18)
式中PI3=PI4=kp2+ki2/s是外环控制器的比例、积分系数。其控制器框图如图5所示。
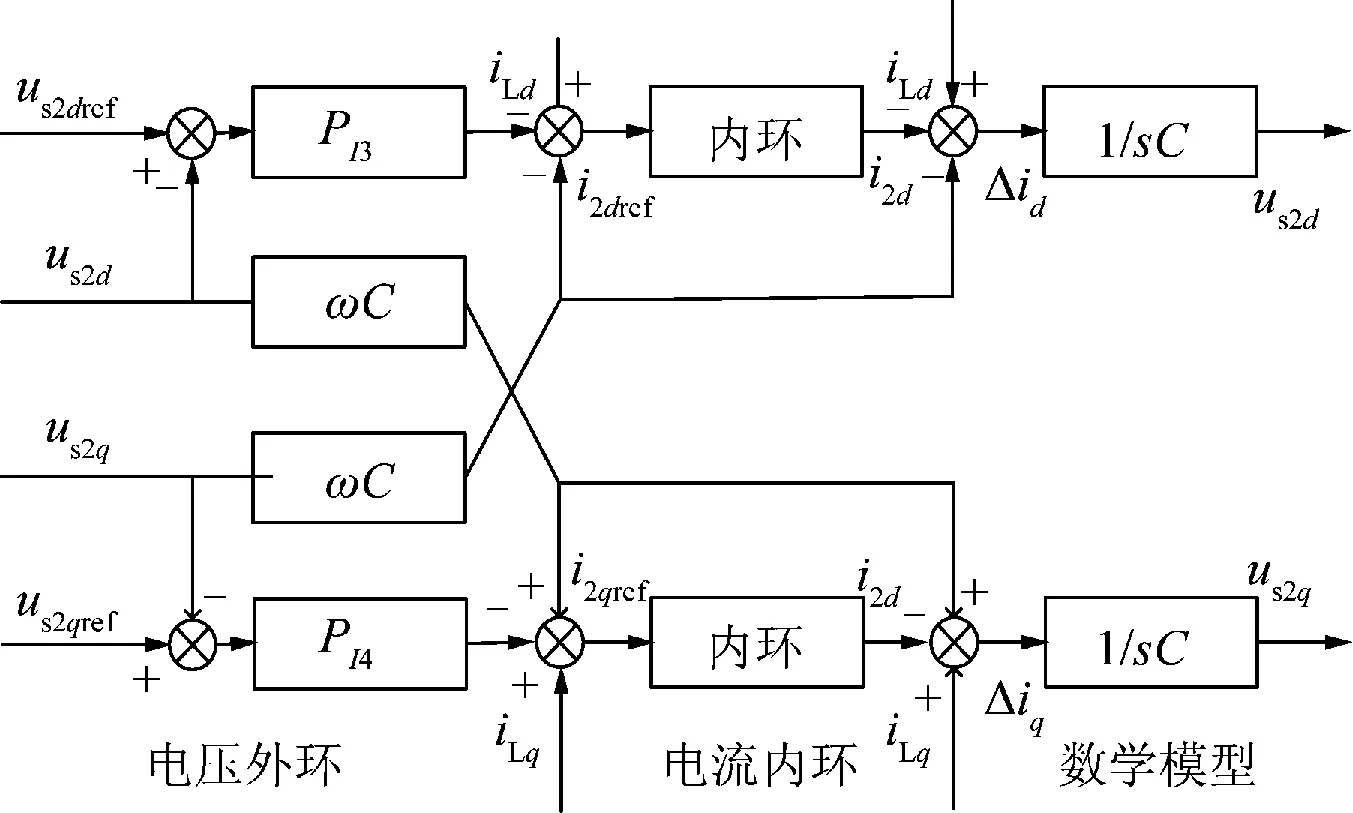
图5 外环电压控制器Fig.5 Outer-loop voltage vector controller
3 VSC-HVDC系统控制参数整定方法
电压源换流站的稳定运行与其控制策略的优劣紧密相关,而控制策略的实现最终又决定于控制系统的控制参数。因此,对控制系统的参数进行整定,选取合适的控制参数对系统的稳定运行至关重要。
3.1 内环电流控制器PI参数整定
分析图3,可得内环电流PI控制器的开环传递函数Gio(d-q轴Gio相同)为
(19)
取kp1,ki1分别为
(20)
式中α为时间常数,为了实现内环电流的快速响应,一般取为几ms[13],将式(20)代入式(19)得:
(21)
此时,内环电流PI控制器的闭环传递函数Gic为
(22)
这样,内环电流PI控制系统就简化成一阶系统,实现了d-q轴电流i2d、i2q对外环输出参考值i2dref、i2qref的无差跟踪。
3.2 外环电压控制器PI参数整定
将电流内环的闭环传递函数Gic代入图5,忽略干扰信号iLd、iLq的作用,则外环电压的开环传递函数Guo(d-q轴Guo相同)为
(23)
式中Ti=kp2/ki2。由式(23)可知外环电压的开环传递函数有2个为0的极点,此时不能采用零极点互消的方法来设计控制参数,否则系统将会失稳。本文采用对称最优法[16]来确定外环电压控制器的参数。整理式(23)并写成频域形式:
(24)
则Guo(jω)的相频表达式为
∠Guo(jω)=-180°+arctan(ωTi)-arctan(ωα)
(25)

根据奈奎斯特稳定判据,相位裕量φM定义为
(26)
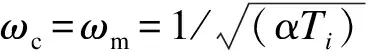
(27)
故选取合适的α,n值,便可获得外环电压控制器的参数。
4 仿真研究
为了验证本文所设计控制器及其参数整定方法的有效性,在PSCAD/EMTDC中建立了向无源网络供电的两端VSC-HVDC仿真系统,如图1所示,其系统参数见表1。分别采用第2节设计的PI双闭环和无源双闭环控制器,进行对比仿真分析。2种方法的外环控制器采用相同的PI参数来保证仿真分析的有效性。PI双闭环控制器的参数采用第3节设计的整定方法来确定,见表2,取α=0.5ms,n=4。仿真在负荷功率变化和电压下降2种工况下进行。
表1 VSC-HVDC系统参数
Table 1 VSC-HVDC system parameters

表2 控制器参数Table 2 Controller parameters

4.1 有功功率增加
无源网络初始负荷S=(150+j60)MVA,在t=0.5 s时,有功负荷增加150 MW。
图6给出了2种控制方式下负载d-q轴电压、电流仿真波形。对比分析可知,无源控制下系统的响应更好。当负载有功功率发生变化时,负载电压产生一定的波动,但无源控制下波动幅度更弱、响应速度更快、稳态误差更小;负载d轴电流经过短暂波动后能稳定在新的期望值,q轴电流变动很小,控制参数选择合理。
图7给出了无源控制下负载交流电压、电流和功率的仿真波形。由图7(a)可以看出,负载有功增加时,交流电压会出现一个很小的跌落,此时负荷侧交流电压控制器动作,使交流电压迅速恢复稳定,同时增大电流的有功分量i2d使交流电流的幅值变大,满足负载的有功需求,如图7(b)和图7(c)所示。达到稳态后,系统交流电压和电流正弦对称,频率稳定,无源控制器工作正常。

图6 2种控制方式下负载d-q轴电压电流波形Fig.6 Simulated voltage and current waveform in synchronous reference frame under two control modes

图7 无源控制下负载电压、电流和功率波形Fig.7 Simulated waveform of voltage, current and power under passive control strategy
4.2 交流电压下降
无源网络初始负荷S=(300+j60)MVA,在t=0.5s时负载交流电压发生0.1 pu的跌落。
图8给出了2种控制方式下负载d-q轴电压电流仿真波形。从图8可以看出,2种控制方式下负载的交流电压和电流都能稳定在新的期望值上,波动幅度都在合理范围内。相比于PI控制,无源控制下系统的动稳态性能更好。
图9给出了无源控制下负载交流电压、电流和功率的仿真波形。由图9(a)可以看出,无源控制器动作迅速,负载交流电压能很快达到新的稳态值。由功率计算公式S=3U2/Z=3I2Z知,交流电压减小时,负荷消耗的有功和无功功率均会有所下降,同时交流电流幅值变小,如图9(b)和图9(c)所示。
5 结 论
(1)本文基于VSC-HVDC系统向无源网络供电的工作原理和特点,建立系统在d-q同步旋转轴下的欧拉-拉格朗日数学模型,设计PI双闭环和无源双闭环2种控制器,并提出基于对称最优法的外环控制器参数整定方法。
(2)在PSCAD/EMTDC中建立向无源网络供电的VSC-HVDC仿真系统。仿真结果表明,在有功负荷增加、交流电压下降等暂态过程中,无源双闭环控制器与PI双闭环控制器都可以实现电压、电流的快速精准控制,使无源网络电压稳定在给定值。相对而言,无源双闭环控制下系统的超调量、稳态误差更小,动态性能更好。
(3)仿真结果也表明提出的控制参数整定方法是正确、有效的,不仅响应速度快,而且具有一定的抗干扰性。

图8 2种控制方式下负载d-q轴电压电流波形Fig.8 Simulated voltage and current waveform in synchronous reference frame under two control modes

图9 无源控制下负载电压、电流和功率波形Fig.9 Simulated waveform of AC voltage, current and power under passive control strategy
[1]汤广福.基于电压源换流器的高压直流输电技术[M].北京:中国电力出版社,2009:121-150.
[2]FLOURENTZOU N,AGELIDIS V G.VSC-based HVDC power transmission systems:an overview [J].IEEE Transactions on Power Electronics,2009,24(3):594-599.
[3]郑超,杨金刚,滕予非,等.LCC与VSC型直流馈入对弱受端电网特性的影响[J].电力建设,2016,37(4):84-90. ZHENG Chao,YANG Jingang,TENG Yufei,et al.Impact of LCC-HVDC and VSC-HVDC infeed on weak-receiving-end grid characteristics[J].Electric Power Construction,2016,37(4):84-90.
[4]STENDIUS L,JONES P.Powerful platform[J].IEEE Power Engineering Journal,2006,20(5):34-37.
[5]郭春义,赵成勇.电压源换流器高压直流输电的控制策略及其参数优化[J].中国电机工程学报,2010,30(15):1-9. GUO Chunyi,ZHAO Chengyong.Novel control strategy for VSC-HVDC and controller parameters optimization[J].Proceedings of the CSEE,2010,30(15):1-9.
[6]赵成勇. 基于有功和无功独立调节的VSC-HVDC控制策略[J]. 电力系统自动化,2005,29(9):20-24. ZHAO Chengyong.VSC-HVDC control strategy based on respective adjustment of active and reactive power[J].Automation of Electric Power Systems,2005,29(9):20-24.
[7]赵成勇,马国鹏.向无源网络供电的VSC-HVDC调节特性研究[J]. 华北电力大学学报,2008,35(6):39-43. ZHAO Chengyong,MA Guopeng.Research on characteristics of regulation of VSC-HVDC supplying power to passive network[J].Journal of North China Electric Power University,2008,35(6):39-43.
[8]杨用春,赵成勇.向无源网络供电的VSC-HVDC控制性能实验研究[J].电力系统保护与控制,2009,37(21):31-35. YANG Yongchun,ZHAO Chengyong.Experimental study on control performance of VSC-HVDC connected to passive network[J].Power System Protection and Control,2009,37(21):31-35.
[9]管敏渊,徐政.MMC型柔性直流输电系统无源网络供电的直接电压控制[J].电力自动化设备,2012,32(12):1-5. GUAN Minyuan,XU Zheng.Direct voltage control of MMC-base VSC-HVDC system for passive networks [J].Electric Power Automation Equipment,2012,32(12):1-5.
[10]蔡新红,赵成勇.向无源网络供电的MMC-HVDC控制与保护策略[J].中国电机工程学报,2014,34(3):405-414. CAI Xinhong,ZHAO Chengyong.Control and protection strategies for MMC-HVDC supplying passive networks[J].Proceedings of the CSEE,2014,34(3):405-414.
[11]管敏渊,徐政.向无源网络供电的MMC型直流输电系统建模与控制[J].电工技术学报,2013,28(2):255-263. GUAN Minyuan,XU Zheng.Modeling and control of MMC-HVDC system connected to passive networks [J].Transactions of China Electrotechnical Society,2013,28(2):255-263.
[12]DU Cuiqing.A novel control of VSC-HVDC for improving power quality of an industrial plant[C]//IEEE Industrial Electronics Conference.Paris,France:IEEE,2006.
[13]EGEA-ALVAREZ A,FEKRIASL S,HASSAN F,et al.Advanced vector control for voltage source converters connected to weak grids[J].IEEE Transactions on Power System,2015,30(6):1-10.
[14]张晓东. PWM整流器的双闭环控制系统设计与仿真研究[J]. 电测与仪表,2009,46(517):73-76. ZHANG Xiaodong.Design and simulation double closed-loop PI regulator of three-phase voltage source rectifier control system[J].Electrical Measurement and Instrumentation,2009,46(517):73-76.
[15]王久和.无源控制理论及其应用[M].北京:电子工业出版社,2010:129-138. WANG Jiuhe.Passivity-based control theory and its applications[M].Beijing:Publishing House of Electronics Industry,2010:129-138.
[16]Bajracharya C,MOLINAS M,SUUL J A,et al.Understanding of tuning techniques of converter controllers for VSC-HVDC[C]//Proceedings of Nordic Workshop on Power and Industrial Electronics,Nordic,2008.
(编辑 张媛媛)
VSC-HVDC Controller and PI Parameters Tuning in Supplying Passive Networks
LI Xiangyang1, LIU Yingmei2, WANG Mingdong1
(1. School of Electrical Engineering, Zhengzhou University, Zhengzhou 450001, China; 2. China Electric Power Research Institute, Beijing 100192, China)
The VSC-HVDC (voltage source converter based high voltage direct current transmission) system has a good application prospect in supplying power to the passive network. Firstly, this paper analyzes the system structure and working principle of VSC-HVDC in passive network power supplying and develops its Euler Lagrange (EL) model ind-qsynchronous reference frame. At the same time, two controllers including a PI double closed-loop controller and a passive double closed-loop controller are designed. Then, this paper presents the parameters tuning method of outer-loop controller based on the symmetrical optimum method. Under different operating conditions including power change of passive network and voltage drop, VSC-HVDC system with a PI double closed-loop controller or a passive double closed-loop controller is simulated by software PSCAD/EMTDC. The simulation results show that the proposed control parameter tuning method is correct, the designed passive double closed-loop controller and PI double closed-loop controller can realize the fast and precise control of voltage and current, and the voltage of the passive network can be stabilized at a given value. Relatively speaking, the dynamic performance of passive double closed-loop controller is better.
voltage source converter based high voltage direct current transmission (VSC-HVDC); passive network; passive controller; double closed-loop control; PI parameters tuning
国家自然科学基金项目 (51407164)
TM 72
A
1000-7229(2016)07-0071-07
10.3969/j.issn.1000-7229.2016.07.010
2016-03-10
李向阳(1989),男,硕士,主要研究方向为柔性直流输电系统的运行分析及控制;
刘应梅(1976),女,博士,高级工程师,主要研究方向为电网规划及运行控制;
王明东(1971),男,博士,副教授,研究方向为电力系统稳定分析与控制、智能系统理论在电力系统中的应用。
Project supported by National Natural Science Foundation of China(51407164)

