基于K-means聚类的有序充放电多目标调度模型
王雅,曾成碧,苗虹,刘广
(四川大学电气信息学院,成都市610065)
基于K-means聚类的有序充放电多目标调度模型
王雅,曾成碧,苗虹,刘广
(四川大学电气信息学院,成都市610065)
针对电动汽车无序充电对配电网的负面影响,该文设计了基于K-means聚类的有序充放电多目标调度模型。首先,以私家车为研究对象进行充电负荷的不确定性建模;其次,根据电动汽车充电桩的空间分布实现有效聚类,形成等效节点以及所对应的代理商;构建以减小峰谷差和代理商调度偏差为目标的第一阶段模型,第二阶段模型以用户充电成本最小为目标,每辆电动汽车的充电需求为决策量;然后将2个目标函数通过单一化处理达到综合最优;最后,在MATLAB平台上采用粒子群优化算法进行求解,算例仿真表明该文提出的调度优化模型在削峰填谷与提高用户经济性方面效果突出。
有序充电;聚类;调度;粒子群算法
0 引 言
随着石油资源的枯竭和可再生能源技术的突飞猛进,电动汽车的发展与推广已势不可挡[1]。用户行驶习惯等不确定因素可能影响电网运行的可靠性,因此,制定合理有效的充放电调度策略对于减小电动汽车接入对电网的影响具有积极作用。
V2G(vehicle-to-grid)指电动汽车作为一种分布式的负荷或者电源,接入电网后释放存储在其动力电池内的电能,可以为电网的运行提供调峰、调频等服务[2-4]。通过有效调节电动汽车的充放电过程,不仅可以削弱电动汽车规模化发展对电力系统造成的负面影响,而且还能降低总成本与系统网损、平抑可再生能源的间歇性[5]。目前,针对电动汽车与电网双向互动的研究,国内外学者提出了多种调度优化策略。文献[6]提出了一种电力市场环境下的电动汽车调度方法,通过选择电价较低时段充电和向系统提供调频或旋转备用,来使电动汽车的总充电成本最小化;文献[7]提出一种基于拉格朗日松弛法的分布式充放电控制方法,实现了电动汽车与发电机组的协调运行并降低发电成本;文献[8]建立了以负荷峰谷差最小化为优化目标的计及用户行驶习惯的插电式混合动力汽车(plug-in hybrid electric vehicle,PHEV)智能充电模型,并对各时段的反向放电能力进行评估;文献[9]引入了电动汽车分层分区调度的理念,构建了基于双层优化的可入网电动汽车充放电调度模型,通过优化各代理商的调度计划使负荷方差最小化,实现调峰填谷。
目前大多数对于有序充放电策略的研究未考虑电网、运营商和用户三者之间的有机协调;且代理商也未按照管辖区域内的实际情况而采用统一的调度方法,具有一定的局限性。本文基于电动汽车充电行为特性对大范围分布的充电桩采用K-means聚类[10],根据地理属性将充电桩划分为几类,并分配区域代理商,利用蒙特卡洛方法进行电动汽车的负荷预测,结合各类代理商的调度计划建立多目标有序充放电优化模型,第一阶段以减小峰谷差和代理商调度偏差为目标,第二阶段以用户充电成本最小为目标。最后通过多目标单一化处理,采用粒子群优化算法[11]对所建立的优化模型进行寻优。通过算例仿真分析,验证该模型的可行性和有效性。
1 基于K-means的充电桩空间聚类
1.1 充电桩空间聚类
由于电动汽车充电具有很大的随机性、多样性和分散性等特点,以聚类的方式将电动汽车分类进行调度,可以降低传统调度方式的求解规模和难度。基于K-means算法具有简单易行、适用于大规模数据处理等特点,本文主要应用K-means聚类算法将临近距离的充电桩分类并由所属代理商管辖,有利于代理商调度计划的准确实施。
1.2 基于K-means算法的充电桩空间聚类
K-means聚类法是典型的基于距离的聚类算法,给定一个数据点集合和需要的聚类数目,算法根据特定的距离函数通过迭代将数据点纳入各聚类域中,实现步骤如下。
(1)指定区域内充电桩个数为m的样本数据集,令迭代次数为R,根据指定聚类数k随机选取k个充电桩作为初始聚类中心Mf(r),其中f=1,2,…,k, k≤m/k;r=1,2,3,…,R。
(2)计算样本空间中每个充电桩Be(e=1,2,…,m)与初始聚类中心的距离D(Be,Mf(r)),形成簇Zf,如果满足式(1),即
(1)
则Be∈Zf,其中η为任意正数。
(3)计算k个新的聚类中心:
(2)
聚类准则函数的计算公式:
(3)
(4)判断聚类是否收敛:
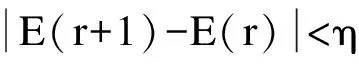
(4)
若合理则迭代终止;否则返回步骤(2)和(3)继续迭代。 如图1所示,根据地理位置将50个充电桩聚类为3类,各分配1、2、3号代理商,根据调度机构指令在各自管辖的区域内实施调度计划引导有序充放电,相比聚类之前降低了代理商对大量电动汽车调度的难度。

图1 基于K-means算法的充电桩聚类Fig.1 Clustering of charging piles based on K-means
2 电动汽车充放电调度构架
电动汽车参与配电网的调度实际上就是通过调控电动汽车的充电行为来实现配电网的削峰填谷、旋转备用和调节频率等功能[12-13]。随着电动汽车的普及,接入配电网的电动汽车具有数量规模大,单台可调度容量小,接入位置分散等特点,不利于进行统一调度。对属性相似的模块分类调度,不仅能减少决策变量,还能降低传统调度方式的求解规模和难度。由于电动汽车的规模庞大,调度机构对每一辆电动汽车一一调度难以实现,而分布式调度的研究还处于初始阶段,有些关键问题还未得到解决。因此本文采用聚类的思想将与中心节点临近的充电桩划分为一类,根据聚类结果给每一类分配一个代理商,调度机构权衡用户及代理商的利益成本和电网的可靠性制定调度计划,各代理商根据调度计划以及所属的实际情况让电动汽车执行充放电调度计划,从而实现配电网、代理商和电动汽车用户之间的耦合,基于K-means聚类的电动汽车充放电调度构架如图2所示。
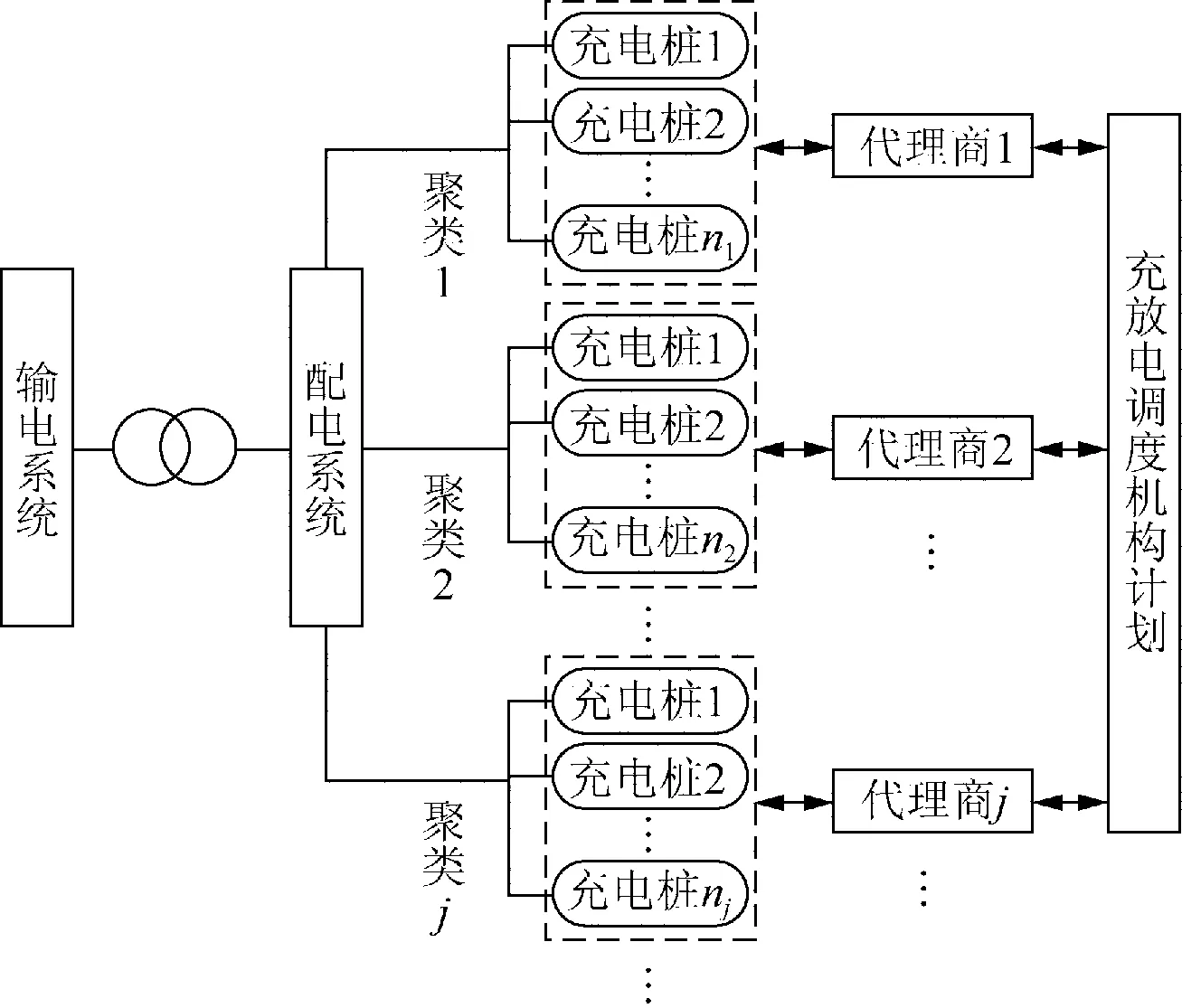
图2 基于K-means聚类的电动汽车充放电调度构架Fig.2 Scheduling structure of electric vehicle charging and discharging based on K-means
3 电动汽车充放电分类调度优化模型
3.1 第一阶段优化模型
(5)
(6)
式中Cb,t为充放电参数,Cb,t=1表示第b个充电桩处于充电状态,Cb,t=0表示第b个充电桩与系统没有电能交换,Cb,t=-1表示第b个充电桩处于放电状态。
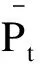
(7)
负荷约束条件:
(8)
多辆电动汽车的充电时间相对集中时,可能导致配电网负荷过重而引起电压下降甚至越限,因此,应当考虑各节点的电压幅值约束:
Umin≤Uβ≤Umax
(9)
式中Uβ为节点β的节点电压。
网络安全约束:
(10)
采用该模型推算乘客上车信息,因为乘客同车次同站点的性质,其刷卡时间相近,因此可以对数据进行聚类,得到公交站点停靠时间段,然后与公交GPS数据的时间字段进行对比分析,配对后得到公交上车站点.
充放电约束:
在任一时刻充电桩b仅有充电、放电,不参与3种状态,即
(11)
各代理商在各时段的调度约束:
(12)
3.2 第二阶段优化模型
设电动汽车电池容量为S,充电时电池起始充电电量为Ss,起始充电时间为Ts,用户需自行设置结束充电时的电池电量为Sd,结束充电时间为Td,用户所需充电电量为Ssoc,则:
Ssoc=Sd-Ss
(13)
结合分时电价,以每辆电动汽车的充电需求为决策变量,用户充电成本最小为目标,目标函数为
(14)
式中:pc,t为t时刻的充电电价;pd,t为t时刻的放电电价;Ci,t为t时刻第i辆电动汽车的充放电状态;Pi,t表示t时刻第i辆电动汽车的充电需求。
充电时间约束:
Tc≤Td-Ts
(15)
电量约束条件:
0≤Ssoc≤S
(16)
0.2≤Ss≤Sd≤1
(17)
本文所建立的2个目标函数是互相影响的,为实现综合最优,本文采用线性加权的方法将多目标函数转化为单目标函数。由于2个目标函数的量纲不同,因此需要通过归一化进行处理:
(18)
λ1+λ2=1
(19)
式中:Y1max表示原始电网负荷曲线的均方差;Y2max表示传统习惯下用户的充电成本;λ1和λ2(λx≥0)为Y1和Y2的权重系数,表示各目标的相对重要程度。
4 模型求解
粒子群优化算法(particle swarm optimization, PSO)是基于群体的演化算法,通过追随当前找到的最优解来搜索全局最优解。本文所建立的模型中,每辆电动汽车在每一个时刻的充放电功率都是一个多变量、多维度、多约束的非线性优化问题,基于PSO算法易于实现、参数少、收敛快等特点,本文采用此算法求解所建立的优化问题,基于K-means聚类的有序充放电调度流程如图3所示。
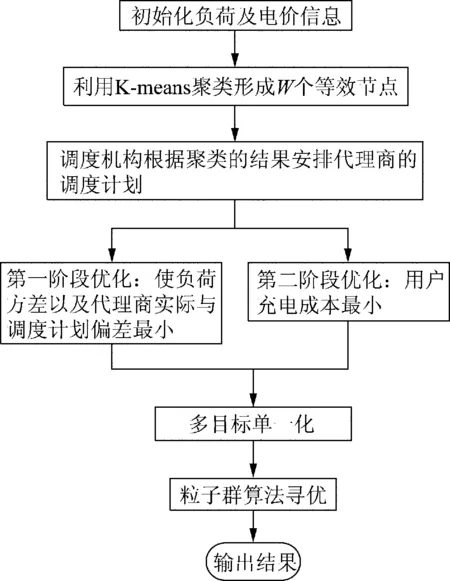
图3 基于K-means聚类的充放电调度流程Fig.3 Charging and discharging scheduling process based on K-means
5 算例分析
5.1 算例介绍
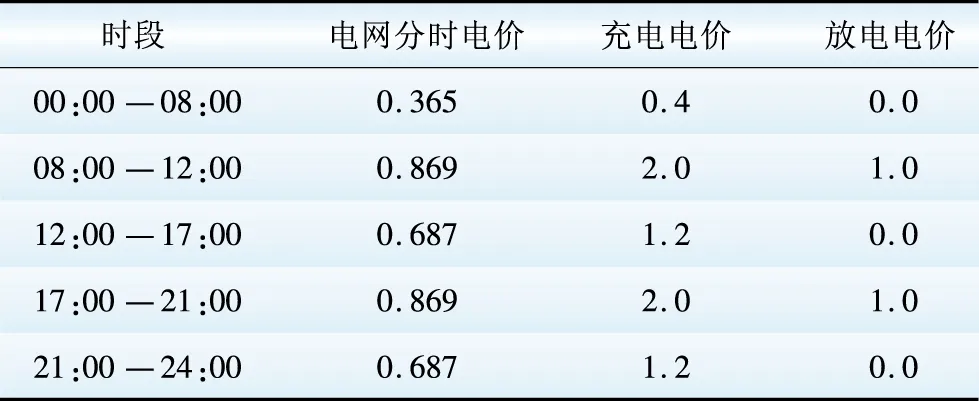
本文以某市A区域配电网典型日负荷曲线为例进行仿真分析。以电动私家车慢充方式为研究对象,仿真采用IEEE 33节点配电网作为算例,为了分析电动汽车优化充电的有效性,假设该配电网区域内有10万辆电动私家车,所有用户均愿意参与有序充放电,此区域有300个充电桩,充电量为5 kW·h,车载充电机功率为3 kW,充电效率为0.9。据K-means聚类算法将充电桩聚类为10个等效节点,并给这些等效节点分配10个代理商。调度周期为24:00—次日00:00,调度时间的单位为h,充电管理方从电网购电的电价采用国内工业用电分时电价的形式。本文旨在“削峰填谷”和提高用户的经济性,因此只考虑峰期放电。电价参数设置如表1所示。
表1 电价参数设置
Table 1 Parameter setting of electricity price
元·(kW·h)-1
5.2 结果分析
5.2.1 充放电调度新方法与无序充电结果对比
为了验证本文所提出的充放电调度优化策略的可行性,本文结合私家车日行驶里程分布等驾驶特性,利用蒙特卡洛仿真法,先模拟无序充电情况下充电需求对电网侧的影响,再将运算结果与有序充放电情形做比较。
由于规模化的电动汽车充电对电网的运行产生很大的负面影响,因此,必须采用有效的控制策略提高电力设备的可靠性。电动汽车具有时间和空间的不确定性,使得运营方难以统一调度管理,本文采用分类调度策略。假设所有用户均愿意参与有序充放电,首先基于K-means聚类算法形成等效节点并且分配各个代理商,调度机构制定各代理商的调度计划,以负荷波动最小和调度偏差最小为第一目标,用户充电成本最小为第二目标,通过多目标单一化,采用粒子群算法寻优。算例中取粒子数N=24,粒子群惯性权重取0.9;最大迭代次数取1 000;速度取值范围为[-0.4,0.4];权重系数体现了各目标函数所占的比重,其选择不同将直接影响优化结果。目前有研究指出[14],通常情况下各目标取相同权重系数可达到综合最优,故本文算例中取λ1=λ2=0.5。仿真结果如图4所示。
由图4可知,无序充电时,充电站因大量电动汽车的接入导致负荷急剧增加,使得配电网负荷曲线出现“峰上加峰”的现象,电力资源有效利用率不足;而有序充放电时,高峰时期的充电负荷被转移到平时段或谷期,有效起到“削峰填谷”的作用,其次峰期有序放电策略使得峰期负荷进一步降低,峰谷差得以有效改善,平时段和谷期的低电价减少了电动汽车用户的充电成本。
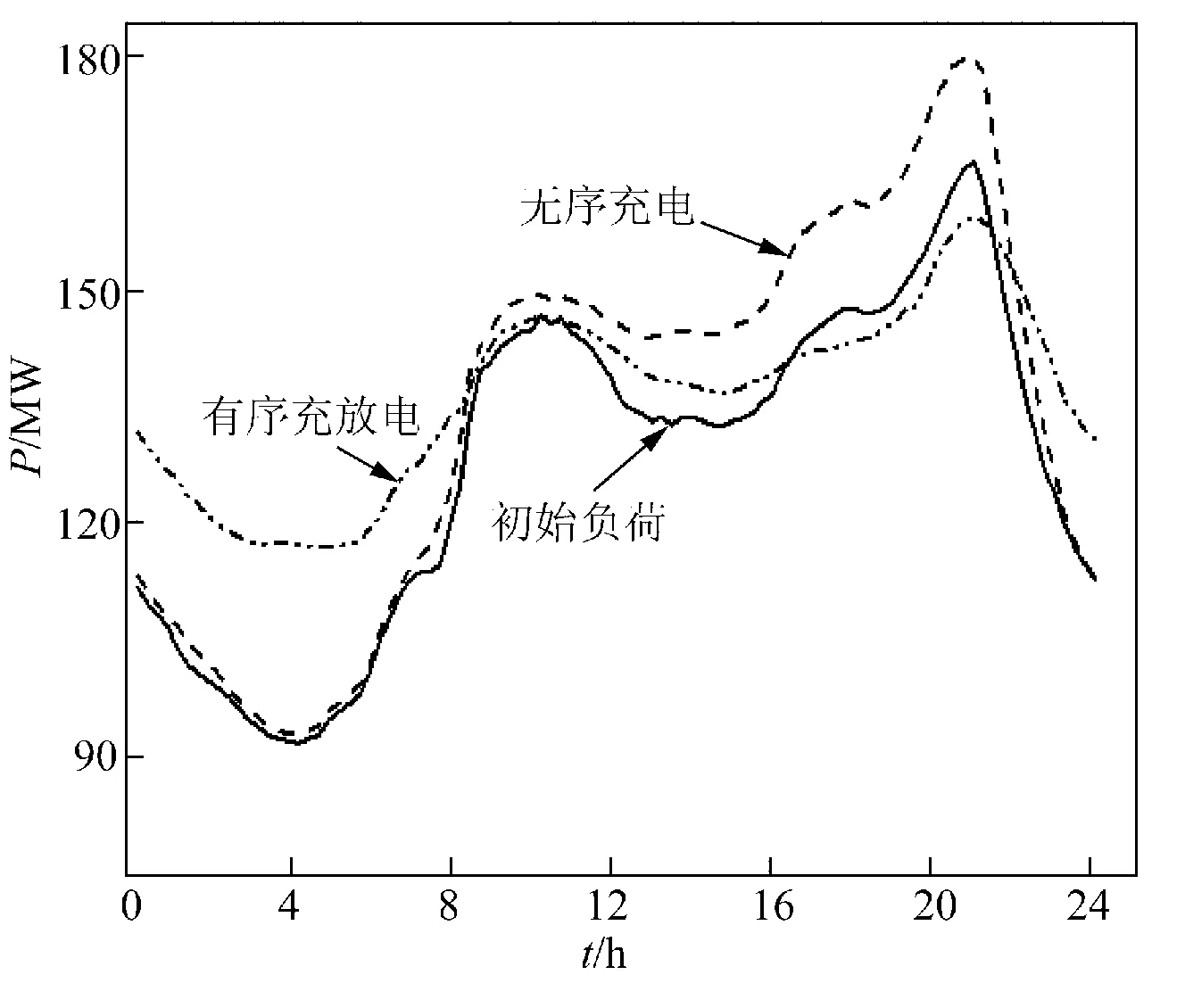
图4 充放电调度新方法与无序充电的对比Fig.4 Comparison between new scheduling method and uncoordinated charging
5.2.2 峰谷差对比及灵敏度分析
根据本文所提出的基于K-means聚类的优化调度策略,引导电动汽车有序充放电以后,负荷峰谷差结果如表2所示。
表2 系统负荷峰谷差对比 MW
Table 2 Comparison of system’s load peak and valley difference
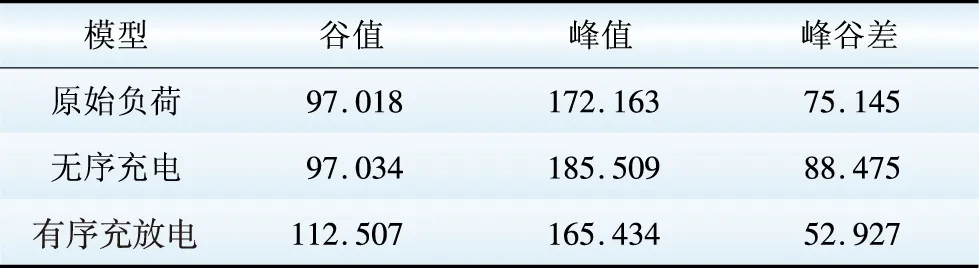
由表2可知,峰谷负荷波动得到明显的改善,在建立的调度优化模型中,惩罚系数δ为对代理商实际充放电行为进行约束的参数,惩罚系数的选取对于优化结果产生不同影响,因此有必要对惩罚系数的取值进行灵敏度分析。以下分别取3种不同的惩罚系数仿真所获得的结果如表3所示。
表3 灵敏度分析
Table 3 Sensitivity analysis
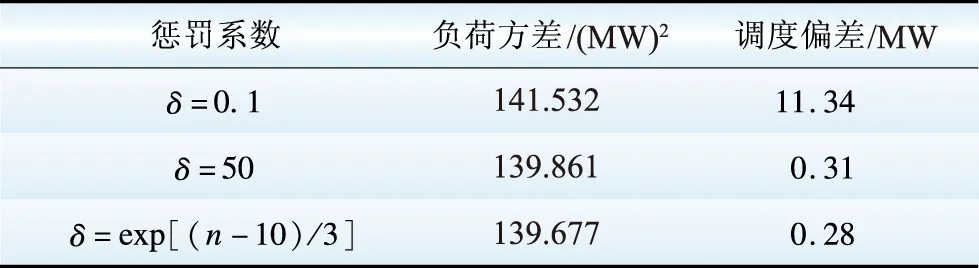
由表3可知,惩罚系数较大(δ=50)时,代理商实际调度与计划相差较小,模型的收敛性比较好,削峰填谷以及用户的成本效果比较明显。惩罚系数较小(δ=0.1)时,代理商实际调度与计划相差较大,不能很好地按照调度计划实施。采用指数规律变化的惩罚系数时,收敛性快,更有优越性。
5.2.3 成本效益分析
电动汽车用户参与有序充放电的调度计划具有随意性,忽略运营商的修建、设备管理等费用,根据不同的用户参与比例计算出的成本效益如表4所示。
表4 不同可控比例下成本效益分析 万元
Table 4 Cost benefit analysis different controllable ratio
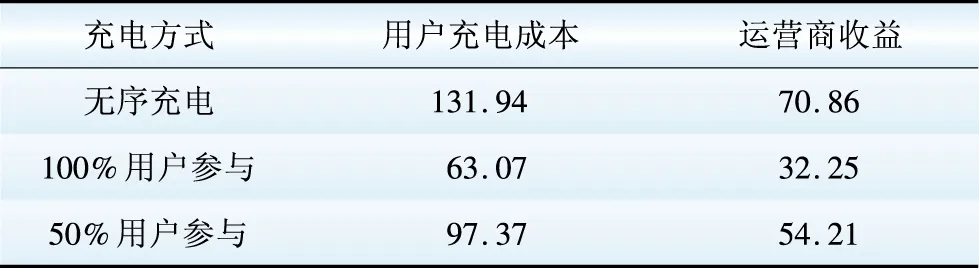
根据计算结果分析可知,本文所提出的优化策略使电动汽车用户的充电费用明显下降,同时运营商的收益随之下降,然而仅以运营商收益最大为目标不利于电网的可靠运行和电动汽车的推广发展。
6 结 论
本文针对电动汽车无序充电对配电网的负面影响以及用户侧的不同需求等问题构建了基于K-means聚类的有序充放电多目标优化调度模型,以私家车为研究对象,根据各电动汽车充电桩的空间分布实现有效聚类,形成等效节点,对每个节点分配代理商并制定各自的调度计划,构建多目标优化调度模型,不仅达到平抑负荷波动的目的,同时也尽可能地减小了用户的充电成本,兼顾了电网、代理商和用户三者之间的综合利益。从仿真结果来看,该策略引导电动汽车尽可能在非高峰期充电、高峰时期放电,缓解了电网的供电压力,达到了“削峰填谷”和用户经济性的双重目的。由于电动汽车现阶段处于推广的初期,规模化投入对电网产生不利影响,本文提出的优化策略具有重要的参考意义。
[1]杨孝纶.电动汽车技术发展趋势及前景(上)[J].汽车科技,2007(6):10-13. YANG Xiaolun.The development trend and foreground of the electric vehicle [J].Auto Mobile Science & Technolog,2007(6):10-13.
[2]GUILLE C,GROSS G.A conceptual framework for the vehicle-to-grid(V2G) implementation[J].Energy Policy,2009,37(11):4379-4390.
[3]SOVACOOL B K,HIRSH R F.Beyond batteries:an examination of the benefits and barriers to plug-in hybrid electric vehicles(PHEVs) and a vehicle-to-grid(V2G) transition[J].Energy Policy,2009,37(3):1095-1103.
[4]孟健,葛贤军,陈乃仕,等.实时电价下电动汽车变参与度动态频率控制策略[J].电力建设,2015,36(7):153-159. MENG Jian,GE Xianjun,CHEN Naishi,et al.EV dynamic LFC strategy with variable participationfactor under RTP[J].Electric Power Construction,2015,36(7):153-159.
[5]胡泽春,宋永华,徐智威,等.电动汽车接入电网的影响与利用[J].中国电机工程学报,2012,32(4):1-10. HU Zechun,SONG Yonghua,XU Zhiwei,et al.Impacts and utilization of electric vehicles integration into power systems[J].Proceedings of the CSEE,2012,32(4):1-10.
[6]CARAMANIS M,FOSTER J M. Management of electric vehicle charging to mitigate renewable generation intermittency and distribution network congestion [C]//Proceedings of the 48th IEEE Conference on Decision and Control. Shanghai,China: IEEE,2009,4717-4722.
[7]邵成成,王锡凡,王秀丽.发电成本最小化的电动汽车分布式充放电控制[J].电力自动化设备,2014,34(11):22-26. SHAO Chengcheng,WANG Xifan,WANG Xiuli,Decentralized EV charge/discharge control with minimum generation cost[J].Electric Power Automation Equipment,2014,34(11):22-26.
[8]李髙望,钱斌,石东源,等.含插电式混合动力汽车的机组组合问题[J].电网技术,2013,37(1):32-38. LI Gaowang,QIAN Bi,SHI Dongyuan,et al,Unit commitment problem considering plug-in hybrid electric vehicle[J].Power System Technology,2013,37(1):32-38.
[9]姚伟锋,赵俊华,文福栓,等.基于双层优化的电动汽车充放电调度策略[J].电力系统自动化,2012,36(11):30-37. YAO Weifeng,ZHAO Junhua,WEN Fushuan,et al.A charging and discharging dispatching strategy for electric vehicles based on bi-level optimization [J].Automation of Electric Power System,2012,36(11):30-36.
[10]黄韬,刘胜辉,谭艳娜.基于K-means聚类算法的研究[J].计算机技术与发展,2011,21(7):54-62. HUANG Tao,LIU Shenghui,TAN Yanna.Research of clustering algorithm based on K-means[J].Computer Technology and Development,2011,21(7):54-62.
[11]施美珍.基于粒子群优化算法的模糊聚类分析及其应用[D].广州:华南理工大学,2012. SHI Meizhen.Fuzzy clustering analysis and application based on Particle Swarm Optimization[D].Guangzhou: South China University of Technology,2012.
[12]赵俊华,文福拴,杨爱民,等.电动汽车对电力系统的影响及其调度与控制问题[J].电力系统自动化,2011,35(14):2-10. ZHAO Junhua,WEN Fushuan,YANG Aimin,et al.Impacts of electric vehicles on power systems as well as the associated dispatching and control problem[J].Automation of Electric Power Systems,2011,35(14):2-10.
[13]唐佳,高爽,王丹,等.入网电动汽车集群的分层控制方法[J].电力建设,2015,36(7):146-152. TANG Jia,GAO Shuang,WANG Dan,et al.A hierarchical control algorithm for aggregated electricvehicles in distribution networks[J].Electric Power Construction,2015,36(7):146-152.
[14]DAWES R M,CORRIGAN B.Linear models in decision making[J].Psychological Bulletin,1974(81):95-106.
王 雅(1990),女,硕士研究生,研究方向为电动汽车有序充电控制;
曾成碧(1969),女,博士,副教授,研究方向为新能源及智能优化控制等;
苗 虹(1971),女,博士,副教授,研究方向为分布式发电和微电网;
刘 广(1990),男,硕士研究生,研究方向为电动汽车充电站规划。
(编辑 张小飞)
Multi-Objective Scheduling Model for Coordinated Charging and Discharging Based on K-means Clustering
WANG Ya, ZENG Chengbi, MIAO Hong, LIU Guang
(School of Electrical Engineering and Information, Sichuan University, Chengdu 610065, China)
Aiming at the serious impact of the uncoordinated charging of electric vehicles on the distribution network, this paper designs a multi-objective scheduling model for coordinated charging and discharging based on K-means clustering. Firstly, we take private cars as research objects for the uncertainty modeling of charging load. Secondly, according to the spatial distribution of the electric vehicle charging pile, the effective clustering is achieved, and the equivalent node and the corresponding agent are formed. The first stage model is constructed to minimize the deviation between the peak-valley difference and the scheduling of agents. At the same time, the second stage model takes the minimum user charging and discharging cost as objective and each electric vehicle charging power as decision content. Then, two objective functions achieve comprehensive optimal through simplified handling. Finally, we adopt particle swarm optimization algorithm on the MATLAB platform to solve the model. The example simulation results show that the proposed scheduling optimization model has remarkable effect in peak cutting and improving user economy.
coordinated charge; clustering; scheduling; particle swarm optimization
科技惠民技术研发项目(2015-HM01-00218-SF)
TM 73
A
1000-7229(2016)07-0099-06
10.3969/j.issn.1000-7229.2016.07.014
2016-03-01

