考虑继电保护故障的输电线路风险评估体系

龚庆武，林燕贞

(武汉大学电气工程学院，武汉市 430072)

考虑继电保护故障的输电线路
风险评估体系

龚庆武，林燕贞

(武汉大学电气工程学院，武汉市 430072)

输电线路在电网中承担着输送和分配电能的作用，其发生故障会给电网运行带来巨大影响，该文提出了一种综合考虑输电线路本身以及线路保护的风险评估体系。利用牛顿同伦算法估计威布尔分布参数，构建继电保护故障率模型；采用效用函数从切负荷损失、线路过负荷损失以及电压越限损失3个指标出发构建严重度模型；利用风险定义计算考虑继电保护设备故障的输电线路的风险，扫描电网的薄弱环节，为制定差异化运维策略提供理论依据。最后以WSCC-9电力系统经典算例为例，进行相关计算仿真，验证了考虑输电线路保护故障特性的电网综合风险评估体系的有效性和实用性。

输电线路；继电保护设备；牛顿同伦算法；威布尔分布；效用函数

0 引 言

输电线路作为发电厂和变电站之间的联络线，实现电力系统的互联以及电能的输送，是电力系统的重要组成部分，一旦发生故障，将会带来不可估量的经济和社会损失。但是输电线路的安全可靠运行不仅和输电线路设备本身相关还和保证输电线路正常稳定运行的保护设备相关。继电保护是保证输电线路安全稳定运行的有力保障，评估继电保护的可靠性是保证输电线路正常运行的必要条件[1]。因此，考虑继电保护设备故障特性对电网进行综合风险评估，找出电网运行薄弱环节，切断风险传递链条，对于实现电网的安全稳定经济运行具有重要意义。

在可靠性工程上，常用的设备故障率分布有伽马分布、威布尔分布和指数分布[2]。文献[3]指出电气设备一般满足“浴盆曲线”，包含早期失效期，偶然失效期以及损耗失效期，威布尔分布的形状参数可以很好地拟合故障率曲线，因而得到广泛的应用。

估计威布尔分布参数时，涉及到非线性方程的求解。目前求解非线性方程一般有Newton迭代法、共轭梯度法等，但是这些方法都有一个致命的缺点，就是局部收敛，要求初值的设定要接近精确值[4]。不动点法、区间估计法可以解决局部收敛问题，但是不动点法计算过程复杂，工作量大；区间估计法需要不断试取合适的区间，计算过程繁琐[5]。现有文献一般采用最小二乘法[6]或者Marquardt法来进行参数估计[7]，但是最小二乘法计算精度不高，当样本点比变量个数明显偏少时，求解会出现严重的舍入误差；Marquardt方法求解过程繁琐，计算量大，不适合工程应用[8]。20世纪发展起来的同伦算法收敛范围大，对初值的要求不苛刻，求解速度快，简单易懂，给非线性方程的求解带来突破性的成就[9]。

本文将建立考虑输电线路继电保护故障特性的电网风险评估体系，利用同伦算法求解继电保护故障率模型；同时引入效用函数，从切负荷损失、线路过负荷损失以及电压越限损失3个指标计算继电保护发生拒动和误动的情况下给电网带来的损失，最后以WSCC-9经典算例为例，进行相关的仿真和计算，求解继电保护不正确动作带来的风险，找出电网的薄弱环节。

1 同伦算法简介

由于非线性方程的复杂性，有时很难直接求得方程组的解，这就需要构造一个简单的迭代方程，从容易求解的方程出发，通过路径跟踪，从而求出复杂方程的精确解，这就是同伦算法的基本思想[9]。

1.1 同伦算法基本原理

考虑n个变量n个非线性方程组的表达式为

(1)

其中，x=(x1，x2，x3，x4，…，xn)∈Rn，fi(x1， x2，x3，x4，…，xn)为定义在区域D上的实函数，i=1，2，3，…，n。

引入向量记号：

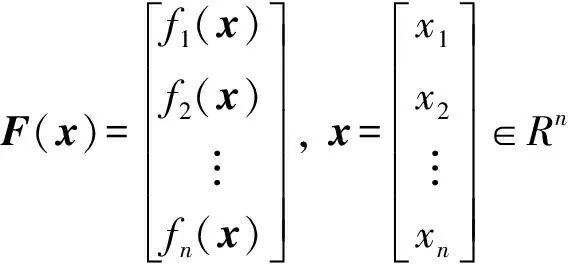
则式(1)可以转换为

F(x)=0

(2)

用牛顿迭代法求解式(2)时，要求初值x0和目标解x*很接近，才能保证迭代序列收敛到x*。但是很多非线性方程很难找到与精确值接近的初值，因此引入大范围收敛的同伦算法[10]。根据同伦算法的定义，引入参数t构造一组同伦映射H(x,t)，使得

H(x,t)=0

(3)

对于同伦映射H(x,t)，要求：当t=0时，H(x,0)=G(x0)；当t=1时，H(x,1)=F(x)，那么求F(x)=0的解就转化为求同伦方程在t=1的解，即：

H(x,0)=G(x0)

(4)

H(x,1)=F(x)

(5)

对于t∈[0 1]，方程H(x,t)=0的解x=x(t)在Rn内是一条连续光滑的曲线，一端为给定初值x0，另一端是H(x,1)=F(x)=0的解，如图1所示。因此，采用基于预测-校正的算法跟踪同伦曲线x(t)，使其从一端给定的初值x0开始，计算曲线上的每一个点xi，其中xi+1是xi先通过预测再校正得来的。

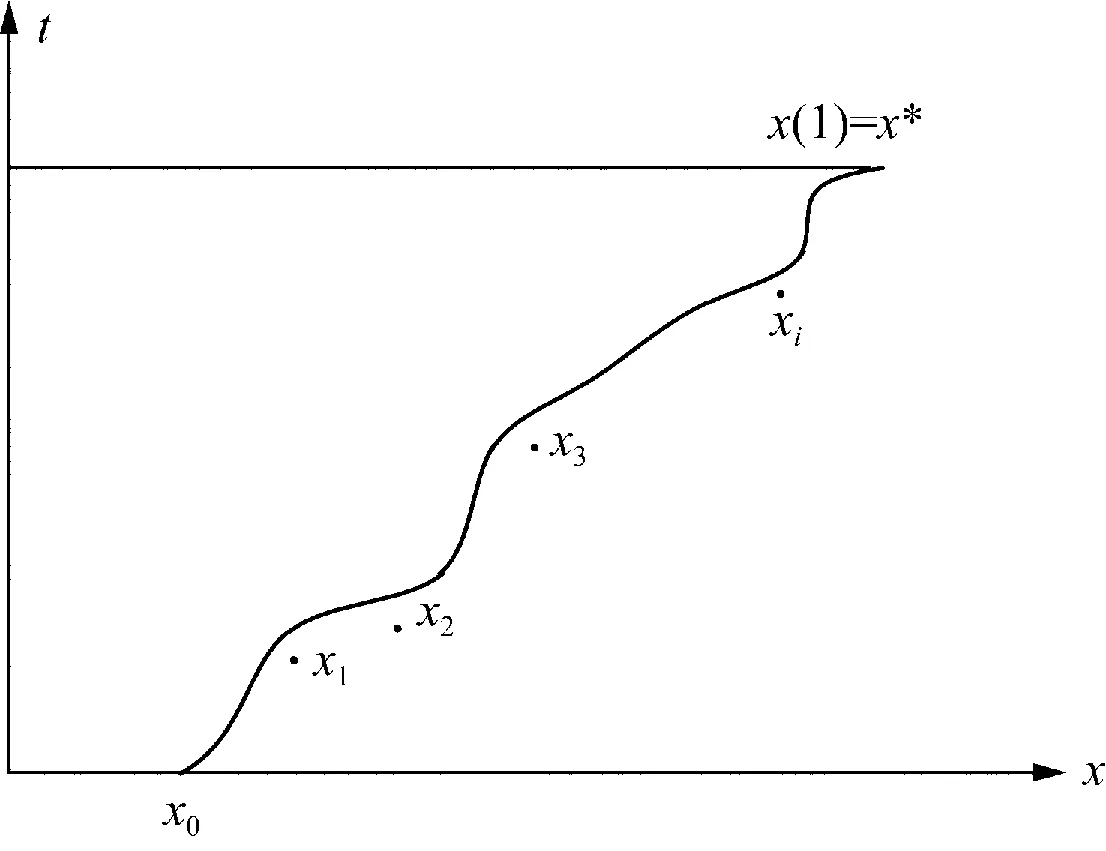
图1 同伦算法示意图Fig.1 Schematic diagram of homotopy algorithm

本文采用牛顿同伦方程组求解非线性方程的参数，表达式[11]为

H(x,t)=tF(x)+(1-t)[F(x)-F(x0)]

(6)

由于x0可以在定义域D中任取，突破了牛顿迭代法对初值选择的限制。

为求解方程(2)的解x，先对同伦方程组H(x，t)=0的参数t进行求导

(7)

(8)

同样地，对式(1)的方程组求导有

(9)

根据式(6)可得：

(10)

(11)

于是式(8)就转化为

(12)

这样就把非线性方程的求解巧妙地转化为微分方程初值问题的求解，即：

(13)

若式(13)存在唯一的解x=x(t)，即为式(2)的解。

1.2 欧拉法预估-四阶龙格库塔法校正

因为故障率的分布模型可以描述为式(13)所示的微分方程初值求解问题，因此，本文采用欧拉法预估-龙格库塔法校正[11]计算微分方程的解。

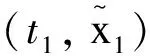
(14)

(15)

由于四阶龙格库塔法的局部截断误差为o(h5)[11]，而且计算速度快，因此本文采用四阶龙格库塔法做数值校正。

令：

(16)

则四阶龙格-库塔的表达式为

(17)

其中：

(18)

经过数次迭代之后求解得到的xn+1不一定是精确解x*，但是按照微分方程数值求解的收敛准则，如果|xn+1-xn|<ε(ε为设置的精度)，那么则认为找到精确解，否则就继续以上两步不断进行预估-校正的过程。

综上所述，非线性方程求解的步骤为：

(1)构造同伦映射H(x,t)，把F(x)嵌入到H(x,t)；

(2)设定迭代起点(t0,x0)，其中t0=0；

(3)采用欧拉法预估-四阶龙格库塔法校正，对解曲线x(t)做数值跟踪；

(4)根据式(15)预测xn的估计值，再采用式(17)对估计值做校正得到修正值；

(5)判断|xn+1-xn|<ε是否成立，若是，则认为xn+1为式(2)的解x*，否则重复以上步骤继续迭代，其中取步长h=1/N，N=1 000，精确度ε取1×10-4。

2 故障率模型的求解

2.1 参数估计

由于继电保护设备在出厂或现场运行前会进行投运前测试，因此本文假设运行的继电保护设备已经过了早期失效期[12]，因此故障率拟合仅选取偶然失效期和损耗期。

一般的威布尔分布包括3个参数β,η,γ[13]，其中β为形状参数，表征分布曲线的形状；η为尺度参数，表征曲线的坐标尺度；γ为位置参数，表征曲线的起始位置，一般情况下取为0[1,14]。基于两参数威布尔分布的设备故障率的表达式为

(19)

分析式(19)可知，求解威布尔分布模型的关键在于β和η。本文采用极大似然函数估计威布尔分布参数[15]。对于可维修的继电保护设备，似然函数为

(20)

式中n为样本容量。

对应的对数似然函数为

(21)

分别对β，η求偏导：

(22)

(23)

那么极大似然函数方程组为：

(24)

(25)

式(24)和(25)为非线性方程，采用牛顿同伦算法求解。

根据第1节的同伦算法理论知识，对式(25)的β和η做第二次求导运算，可得：

(26)

(27)

(28)

(29)

即雅克比矩阵为

(30)

根据同伦算法，迭代公式为

(31)

当k=0时，β0，η0为初值，即只需已知初值再根据式(31)即可估计参数β和η，从而得出威布尔分布的表达式。

2.2 故障率模型的建立

(1)初值的求解。选取2个历史数据(td，λd)和(tg，λg)，构建方程组如式(32)所示，求解β0和η0。

(32)

(2)偶然失效期和损耗期分界点确立。假设总的故障数据有N个，根据故障率的散点图，选取合适的点数M，利用式(31)求解点数为M的参数，对于剩余的(N-M)点采用连接点处的故障率，取定值。M值的选取原则通过寻求min(eRMSE)所得。均方根误差(eRMSE)的表达式为

(33)

式中：λ为分界点的故障率；λi为设备实际的故障率；yi为设备拟合的故障率。

3 输电线路保护风险评估

为了全面、科学分析输电线路保护拒动、误动给电网带来的影响，本文从切负荷损失，线路过负荷损失以及电压越限损失3个指标出发计算风险，其中故障率函数采用威布尔分布，故障严重度模型采用效用函数[16]。

效用函数分为3种：风险厌恶型、风险中立型和风险偏好型，文献[16]指出风险偏好型可以准确构建事故发生后带来的严重度模型，表达式为

s(w)=0.582(ew-1)

(34)

式中w为发生事故后切负荷损失、线路过负荷损失以及电压越限损失，具体表达式参考文献[17]。

综合考虑切负荷损失、线路过负荷损失以及电压越限损失的综合损失为

s(w)=w1sFL(w)+w2sli(w)+w3sVi(w)

(35)

式中：w1、w2、w3为切负荷损失、线路过负荷损失以及电压越限损失3个指标的权重；sFL、sli、sVi分别为切负荷损失、线路过负荷损失以及电压越限损失的严重度。

本文采用层次分析法求解权重，首先根据1-9标度评价标准建立判断矩阵Z为

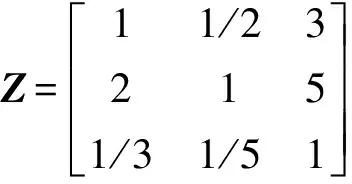
(36)

其次根据式(37)求解切负荷损失、线路过负荷损失以及电压越限损失3个指标的权重分别为0.358，0.475，0.167。

(37)

那么综合考虑输电线路和线路保护的风险表达式为

R=0.8×P2×(1-P1)×s1(w)+
0.2×P2×P1×s2(w)

(38)

式中：P1为继电保护设备对应的一次设备的故障率；P2为线路保护设备的故障率；s1(w)为线路保护设备误动造成的损失；s2(w)为线路保护设备拒动造成的损失。0.2和0.8是参考文献[18]得到的。

分析式(38)可知，考虑一次二次设备风险包括保护拒动和误动带来的风险，所谓继电保护误动就是切除保护所在线路，此时线路为正常运行状态，即式中0.8×P2×(1-P1)；所谓拒动风险是指此时一次设备发生故障，对应的保护拒动，需要相邻的后备保护来切除故障，即式中的0.2×P2×P1。

4 算例分析

记录广东某一地区相同型号，运行环境相似的输电线路保护设备台账以及故障信息，对应不同年份的故障率统计结果如表1所示，故障率分布如图2所示。

表1 继电保护设备故障率统计数据
Table1Statisticsofrelayprotectionequipmentfailurerate

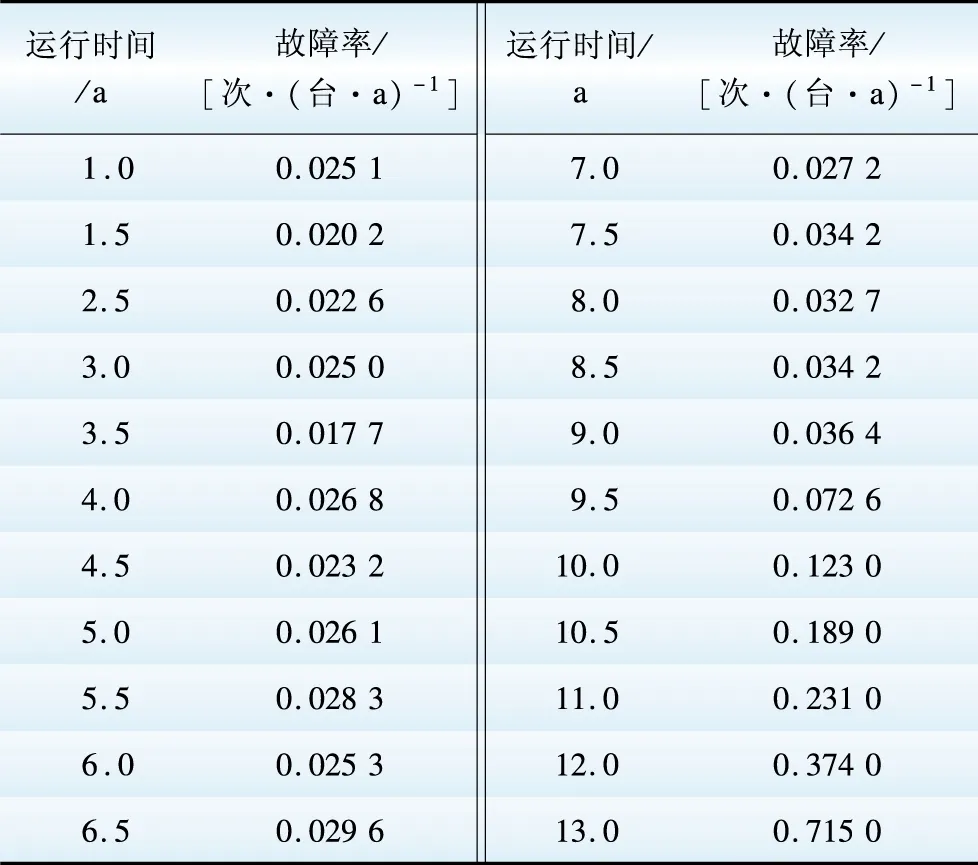
图2 继电保护设备故障率分布曲线Fig.2 Distribution curve of relay protection equipment failure rate

4.1 继电保护故障概率计算

(1)初值的确定。取9年和12年的故障率求解初值β0和η0，根据式(32)求得初始值(β0，η0)=(7.745,13.160)。

(2)分界点的确定。为了建立继电保护设备故障率分布曲线，需要找出偶然失效期和损耗期的分界点，得出关于时间的故障率分布函数。根据图2分析可知，分界点在7～9.5年之间，表2为计算选取不同分界点时，威布尔分布参数的估计值以及对应分界点下均方根误差。

表2 威布尔分布的参数分界点
Table2ParameterdemarcationpointofWeibulldistribution

分析表2可知，在8.5年时，均方根误差最小，为0.0126，因此取第8.5年为偶然失效期和损耗期的分界点。因此，继电保护设备故障率分布函数表达式为

(39)

根据式(39)做继电保护设备的故障率分布拟合曲线如图3所示。

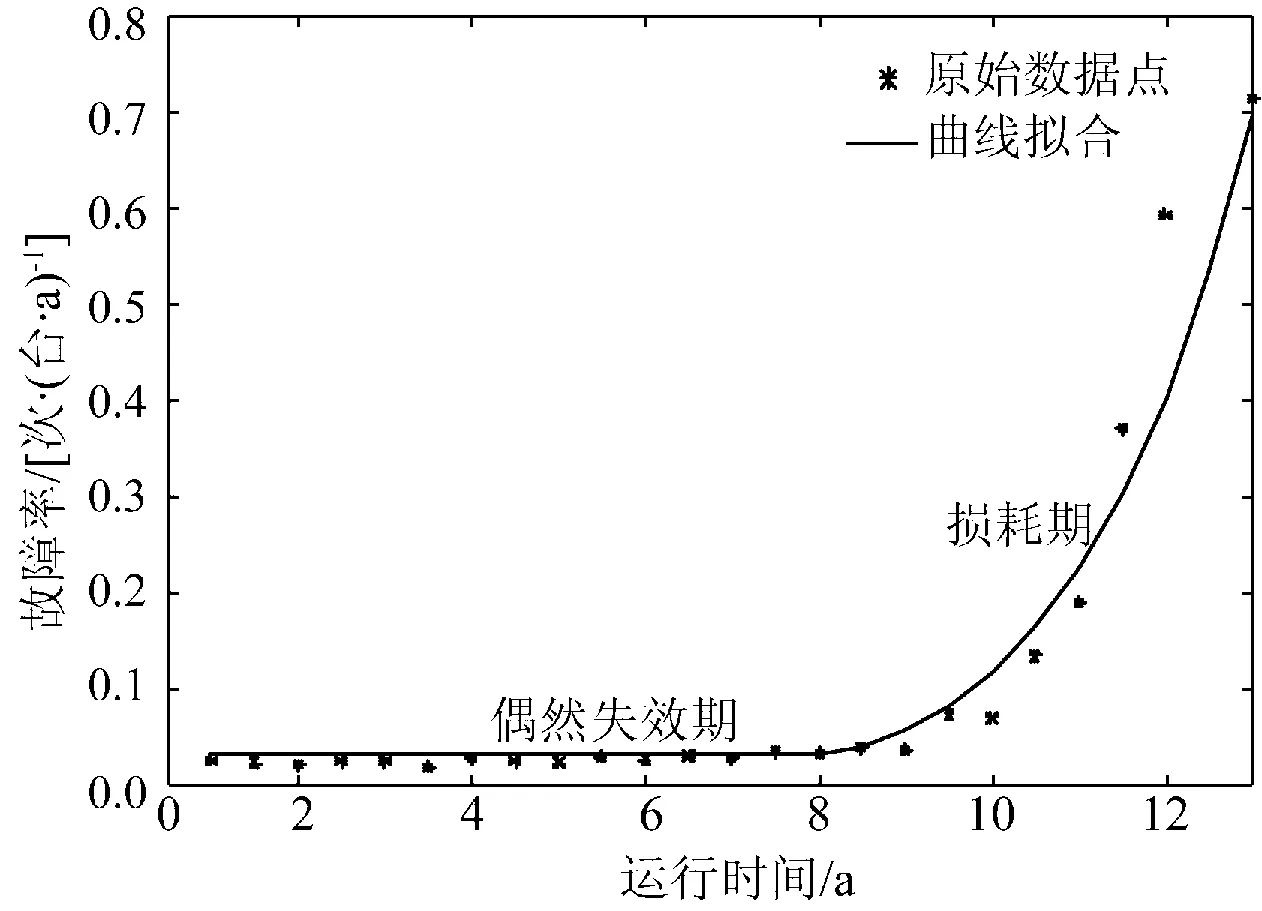
图3 继电保护设备拟合曲线Fig.3 Fitting curve of relay protection equipment

4.2 初值的选择对威布尔分布参数的影响

(1)采用已知的故障率求解初值。选取9年和12年的故障率，根据式(32)求得初始值(β0，η0)=(7.745 0，13.160 0)。

(2)采用rand函数产生随机数作为初始值。利用同伦算法求出的2种初值下的参数(β1,η1) = (7.820 3, 12.761 7)和(β2,η2) = (7.790 3, 13.118 0)，曲线拟合如图4所示。

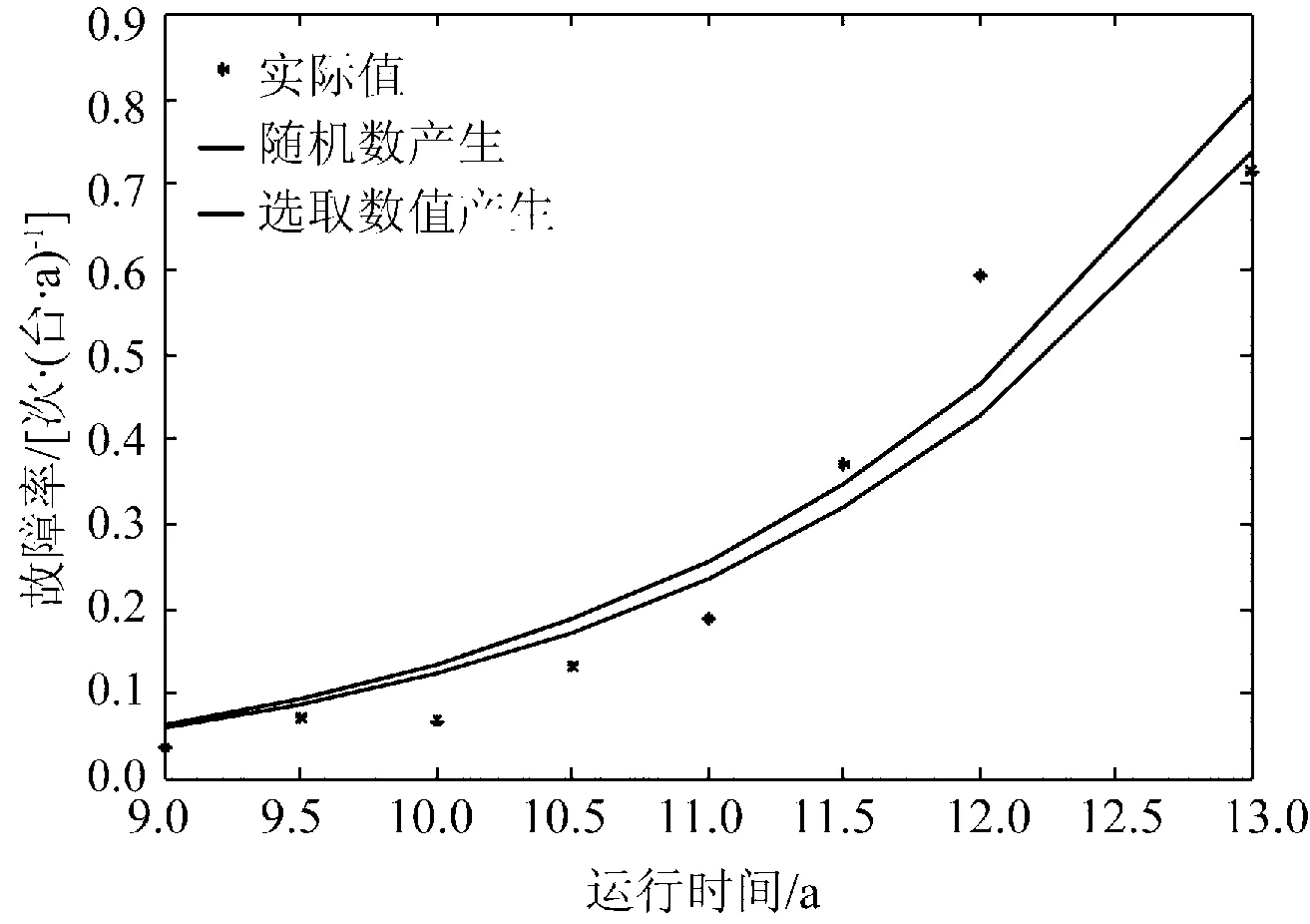
图4 两种不同初值的曲线拟合Fig.4 Curve fitting of two different initials

分析图4可知，采用随机数法和选用特定数值法确定初值得到的故障率曲线，数据均匀地分散在曲线两侧，并且二者曲线几乎重合，所估计的β，η近似相等，即采用牛顿同伦算法求解非线性方程不受初值的影响，具有很强的优越性。

4.3 最小二乘法和同伦算法的比较

同样地，采用最小二乘法估计威布尔分布参数，估计结果如表3所示。

将2种方法得出的参数代入威布尔分布方程，作曲线拟合，结果如图5所示。

表3 基于最小二乘法的参数估计
Table3Parameterestimationbasedontheleastsquaremethod

图5 2种算法下的曲线拟合Fig.5 Curve fitting in two algorithms

为了比较2种算法下曲线拟合的误差，本文采用相对误差[19]来衡量，2种算法下的相对误差如图6所示，相对误差的分布情况如表4所示。

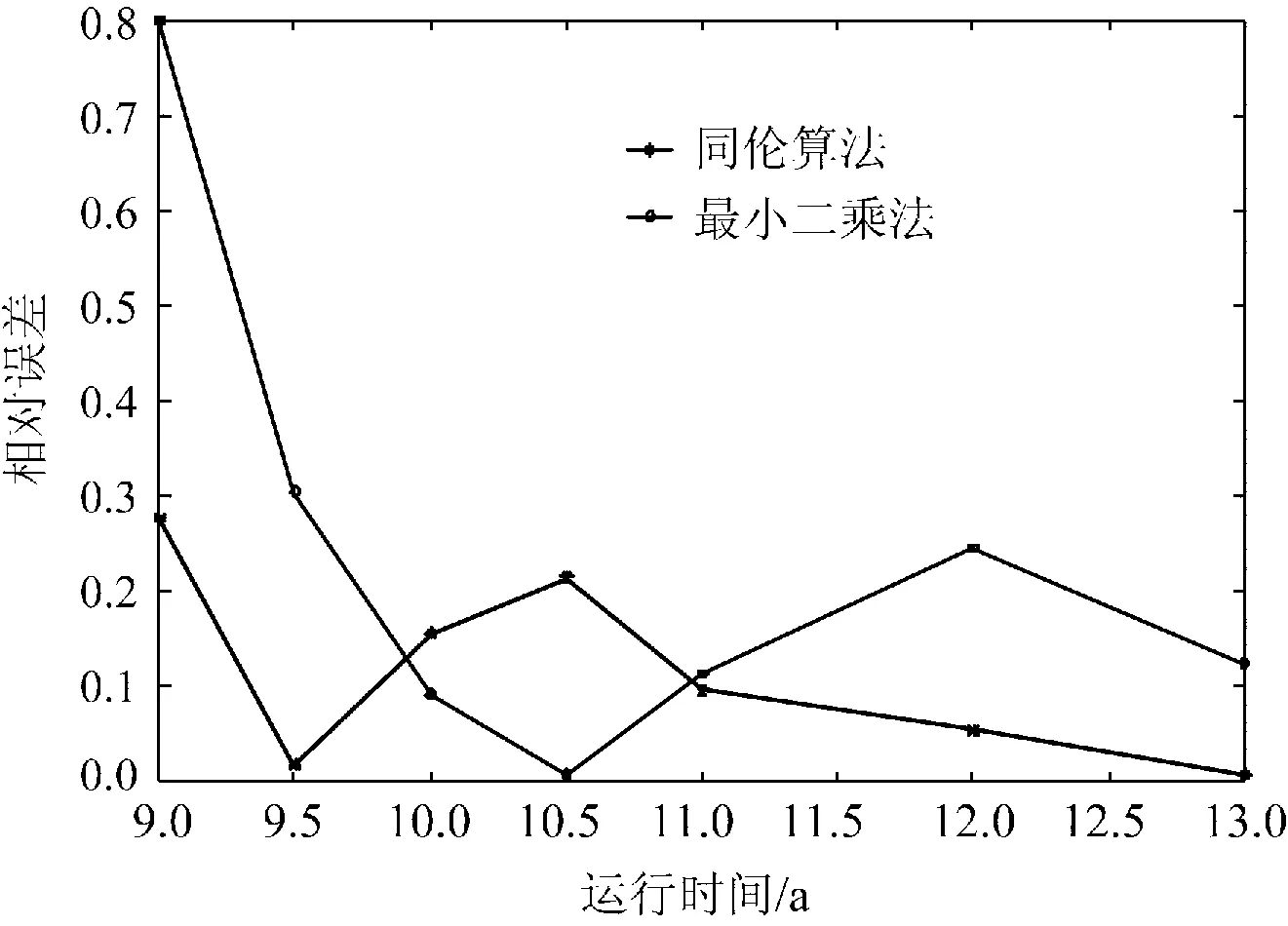
图6 2种算法的相对误差Fig.6 Relative error of two algorithms

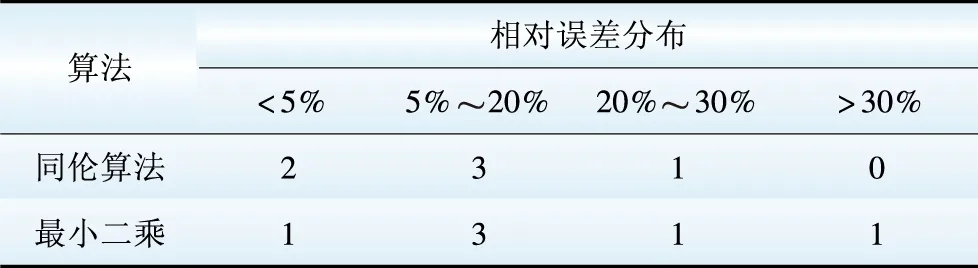
分析表4以及图6可知，采用同伦算法拟合的故障率的相对误差>30%的个数为0，1个位于20%～30%，其他的全部<20%，但是最小二乘法，有1个相对误差>30%，相比较而言，同伦算法拟合效果更好。

4.4 输电线路风险计算

利用中国电力科学研究院PSASP7.0仿真平台，对图7所示的WSCC-9系统进行仿真，仿真和计算保护拒动和误动情况下带来的损失如表5、6所示。

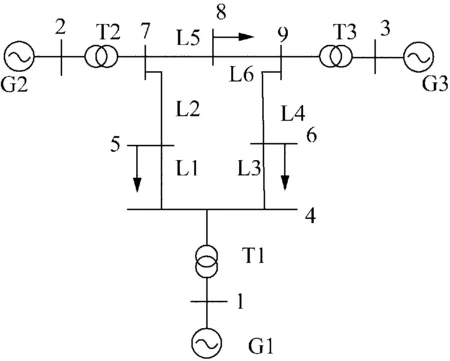
图7 WSCC-9 系统单线图 Fig.7 Single-line diagram of WSCC-9

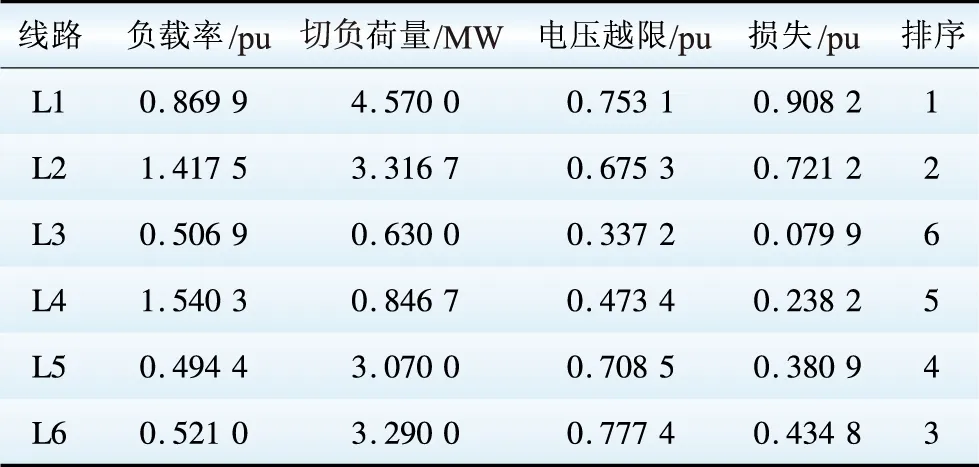
表6 线路正常运行继电保护误动带来的损失Table 6 Loss of maloperation of relay protection under line normal operation

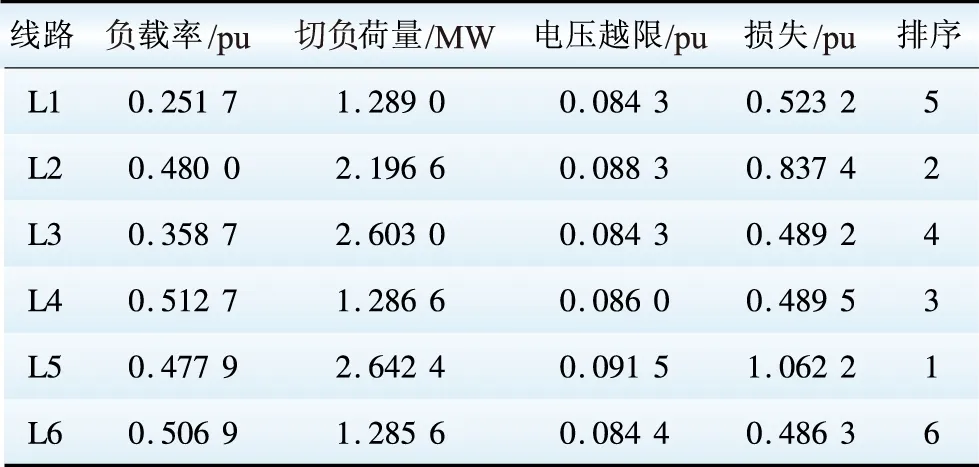
分析表5、6可知，相同线路保护发生拒动和误动给电网带来的损失不同，在线路发生故障继电保护拒动的情况下，若是L1发生故障，此时需要相邻线路保护切除故障，有3种情况：若L1两端保护都拒动，即事故发生的概率为P22×P1，此时需要L2的保护动作以及变压器T2保护动作，即L1，L2以及变压器T2都要断开，计算此时电网损失；若靠近L2的保护拒动，事故发生的概率为P2×(1-P2)×P1，此时只需要L2的保护动作，此时L1，L2要断开，计算此时电网损失；若靠近变压器的保护拒动，事故发生的概率为P2×(1-P2)×P1，需要变压器T2保护动作，此时L1，T2要断开，计算此时电网损失。而且这3种情况是互相独立的，采用概率加和计算，利用PSASP7.0仿真平台可得此时损失最大。同理可得，L2次之，L3的损失最小。在线路正常运行保护误动的情况下，类似于N-1故障，利用PSASP7.0仿真平台计算可得L5保护误动时损失最大，L2次之，L6最小。

[19-20]可得输电线路故障率如表7所示。

表7 输电线路故障率
Table7Failurerateoftransmissionlines

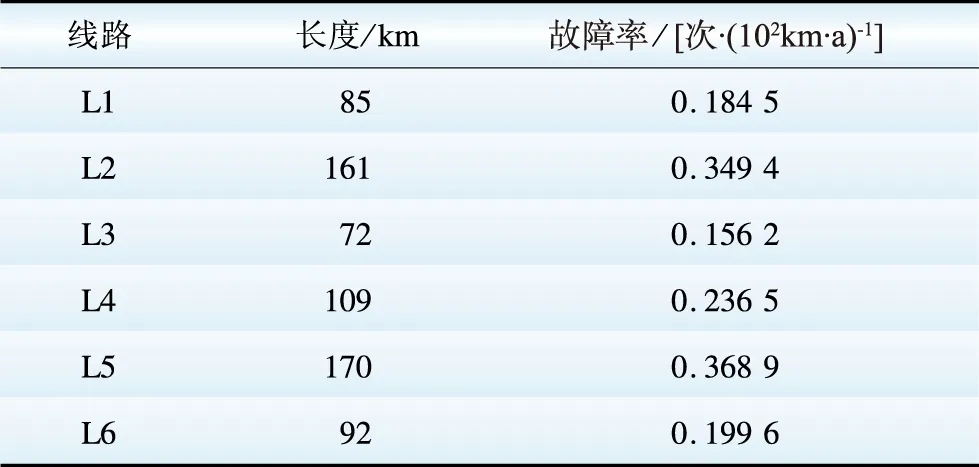
假设继电保护运行8年，根据式(39)计算故障率为0.033 7。根据式(38)计算电网风险以及风险排序如表8所示。

表8 输电线路运行风险指标与排序
Table8Operationriskindexesandsequencesoftransmissionlines

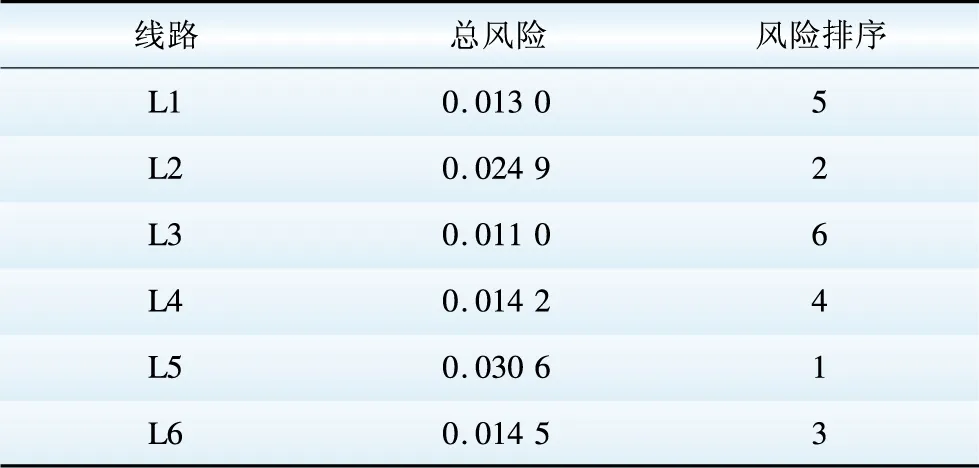
分析表8可知，在由于继电保护不正确动作带来的风险中，L5线路保护风险最大，对系统的危害最大，L2次之，L3最小，需要运行人员在制定检修计划以及差异化运维策略时引起足够的重视。

所谓运维策略指的是设备的日常巡维、特别巡维的工作周期、工作内容及工作要求。由于继电保护设备种类繁多，如果选用相同的巡视周期，必然浪费不必要的人力和物力的投入。但是在风险评估结果分析的基础上，根据风险的结果可以制定不同的巡视周期，对于线路5，由于保护发生故障带来的风险最大，那么日常巡视周期由原来的1月/次缩短为2周/次，对于线路3，由于风险比较小，因此日常巡视周期相应延长为6月/次，即实现差异化运维。

5 结 论

(1)本文采用两参数的威布尔分布，利用收敛范围大的同伦算法求解非线性方程，求解继电保护故障率分布；

(2)采用效用函数从切负荷损失，线路过负荷损失以及电压越限损失3个指标计算损失，求解继电保护不正确动作带来的风险，包括拒动和误动的风险，最后算例表明，综合考虑一次二次设备的风险评估体系能够反映电网的实际运行情况。

6 参考文献

[1]付勇. 电力系统继电保护装置运行可靠性指标的研究[J]. 电力建设,2005,26(10):43-44，47.FUYong.Studyonoperativereliabilityindicesofprotectiverelaysinpowersystem[J].ElectricPowerConstruction,2005,26(10):43-44，47.

[2]周孝信. 电力系统可靠性新技术[M]. 北京： 中国电力出版社, 2014.

[3]高翔.继电保护状态检修应用技术[M].北京: 中国电力出版社， 2008[4]刘杨. 数值同伦算法理论及其应用[D].长春：吉林大学,2008.LIUYang.TheoryandapplicationsofNumericalhomotopymethod[D].Changchun:JilinUniversity, 2008.

[5]张新东. 牛顿—同伦分析法求解非线性方程的一个改进[J]. 新疆师范大学学报(自然科学版), 2010, 29(3):55-58.ZHANGXindong.Newtonhomotopyanalysismethodforsolvingnonlinearequationsofamodified[J].JournalofXinjiangNormalUniversity(NaturalScienceEdition), 2010, 29 (3): 55-58.

[6]张黎,张波. 电气设备故障率参数的一种最优估计算法[J]. 继电器,2005,33(17):31-34.ZHANGLi,ZHANGBo.Analgorithmforoptimalparameterestimationofthefailurerateofelectricalequipment[J].Relay, 2005,33(17):31-34.

[7]孙鹏,陈绍辉,张彩庆. 基于Marquardt法参数估计的变电设备寿命周期故障率评估[J]. 电力系统保护与控制,2012,40(1):85-90.SUNPeng,CHENShaohui,ZHANGCaiqing.AssessmentoffailurerateforsubstationequipmentlifecyslebasedonMarquardtparameterestimationmethod[J].PowerSystemProtectionandControl, 2012,40(1):85-90.

[8]杨梅,周喜超. 基于最小二乘综合权重优化模型的风电场电能质量评估[J]. 电力建设,2014,35(9):93-96.YANGMei,ZHOUXichao.Powerqualityassessmentofwindfarmsbasedoncomprehensiveindexweightoptimizationmodelwithleastsquaremethod[J].ElectricPowerConstruction, 2014,35(9):93-96.

[9]王则柯，高堂安.同伦方法引论[M].重庆：重庆出版社，1990.

[10]黄青群， 朱志斌， 卢钰松. 一般非线性规划的组合同伦牛顿法[J]. 湘潭大学自然科学学报， 2013， 35(1): 21-24.HUANGQingqun，ZHUZhibin，LUYusong.CombinedHomotopyNewtonmethodfornonlinearprogramming[J].NaturalScienceJournalofXiangtanUniversity， 2013， 35(1): 21-24.

[11]颜庆津. 数值分析[M]. 北京：北京航空航天大学出版社， 1992.

[12]冯管印，何川，丁坚勇，等.电气设备故障率演化推算综合算法[J]. 武汉大学学报(工学版)，2014,47(2):244-249.FENGGuanyin，HEChuan，DINGJianyong，etal.Synthesisalgorithmofelectricalequipmentfailurerateevolution[J].EngineeringJournalofWuhanUniversity, 2014, 47(2):244-249.

[13]罗麟. 高压电网继电保护装置可靠性评估[D]. 北京：华北电力大学， 2014.LUOLin.Reliabilityassessmentofthehighvoltageprotectivedevice[D].Beijing:NorthChinaElectricPowerUniversity, 2014.

[14]金良琼. 两参数Weibull分布的参数估计[D]. 昆明：云南大学， 2010.JinLiangqiong.TwoparameterestimationforWeibulldistribution[D].Kunming:YunnanUniversity， 2010.

[15]盛骤，谢式千.概率论与数理统计及其应用[M].北京:高等教育出版社，2004.

[16]张国华, 段满银, 张建华,等. 基于证据理论和效用理论的电力系统风险评估[J]. 电力系统自动化, 2009, 33(23):1-4.ZHANGGuohua,DUANManyin,ZHANGJianhua,etal.Powersystemriskassessmentbasedontheevidencetheoryandutilitytheory[J].AutomationofElectricPowerSystem, 2009, 33 (23): 1-4.

[17]韩泽文,苏永清,岳继光,等. 电网脆弱性综合指标建立与评估[J]. 电力建设,2015,36(8):89-94.HANZewen,SUYongqing,YUEJiguang,etal.Establishmentandassessmentofpowergridvulnerabilitycomprehensiveindex[J].ElectricPowerConstruction, 2015,36(8):89-94.

[18]广东电网公司继电保护设备状态评价与风险评估工作方法[R].广州：南方电网科学研究院,2013.

[19]熊世旺,郭创新,何宇斌,等. 考虑线路介数和well-being风险贡献度的电网脆弱线路评估[J]. 电力建设,2015,36(12):84-90.XIONGShiwang,GUOChuangxin,HEYubin,etal.VulnerablelineevaluationinpowergridconsideringlinebetweennessandWell-beingriskcontributiondegree[J].ElectricPowerConstruction, 2015,36(12):84-90.

[20]梁志峰. 2011-2013年国家电网公司输电线路故障跳闸统计分析[J]. 华东电力, 2014, 42(11):2265-2270.LIANGZhifeng.StatisticalanalysisoftransmissionlinefaulttrippinginstategridcorporationofChinain2011-2013[J].EastChinaElectricPower, 2014, 42 (11):2265-2270.

(编辑 张小飞)

Risk Assessment System of Transmission Line Considering Relay Protection Fault

GONG Qingwu，LIN Yanzhen

(School of Electrical Engineering, Wuhan University, Wuhan 430072, China)

The transmission line plays a role of power transmission and distribution function in the power grid, whose failure will bring enormous influence on the operation of power grid. This paper proposes a risk assessment system with comprehensively considering the transmission line and line protection. We use Newton-Homotopy algorithm to estimate the parameters of Weibull distribution and construct the fault rate model of relay protection; adopt utility function to construct the model of severity including the loss of load, line overload and voltage limit; and use the definition of risk to calculate the risk of transmission line under relay protection equipment fault, scan the weakness of grid, and provide theoretical basis for setting the differential operation strategy. Finally, the calculation and simulation results of the WSCC-9 test system verify the correctness and efficiency of the comprehensive risk assessment system of grid with considering the protection fault characteristics of transmission line.

transmission line; relay protection equipment; Newton-Homotopy algorithm; Weibull distribution; utility function

国家科技支撑计划资助项目(2013BAA02B01)

TM 754

A

1000-7229(2016)07-0141-08

10.3969/j.issn.1000-7229.2016.07.020

2016-03-12

龚庆武(1967)，男，教授，博士生导师，研究方向为电力系统运行与控制、优化调度等；

林燕贞(1991)，女，硕士研究生，研究方向为电力系统继电保护风险评估。

Project supported by the National Science and Technology Support Program(2013BAA02B01)