光伏发电系统的时序概率模型研究
金黎明,周宁,冯丽,范飞,赵渊
(1.国网重庆市电力公司,重庆市 400015;2.输配电装备及系统安全与新技术国家重点实验室(重庆大学),重庆市 400044)
光伏发电系统的时序概率模型研究
金黎明1,周宁1,冯丽1,范飞2,赵渊2
(1.国网重庆市电力公司,重庆市 400015;2.输配电装备及系统安全与新技术国家重点实验室(重庆大学),重庆市 400044)
随着光伏发电在电网中的应用越来越广泛,如何建立有效的光伏发电概率模型成为亟待研究的问题。传统的光伏发电模型一般基于参数估计,需要对辐照度的概率分布形式做出预先假设,且无法计及日总辐射与小时辐射间的内在“加和”约束。为了克服传统光伏发电模型存在的不足,利用解集及条件核密度估计技术提出一种新的光伏发电时序概率模型。该模型属于非参数模型,无需对辐照度的概率分布形式做出任何限制,不仅能够计及日/小时辐照度之间的时序相关性,而且能够计及日总辐射与小时辐射间的内在“加和”约束,从而可以更加精确地反映光伏发电的随机变动规律。算例分析表明该模型能够以更高精度反映辐照度的变动规律,因而具有明显的优越性和实用性。
光伏发电;概率模型;加和约束;时序相关性;条件核密度估计
0 引 言
随着光伏、风能等大规模可再生能源不断接入电网,其输出功率的随机性和间歇性加重了电网规划和运行的不确定性,因此,针对新能源发电的不确定性进行研究,提出有效的概率模型成为当下研究的热点。
对光伏发电系统的太阳辐照度概率模型研究,现广泛采用正态分布模型[1]或Beta分布模型[2-3],该类模型仅考虑了太阳辐照度的随机分布规律,而忽略了太阳辐照度连续随机变化过程的时序相关特点及日总辐照度与小时辐照度间的内在“加和”约束。基于此,文献[6]根据太阳辐照度的时间函数描述其时序变动规律,并在此基础上叠加对应的随机波动建立了太阳辐照度的时序动态概率分布模型;文献[7]基于条件概率及两变量核密度估计理论建立了光伏出力的时序概率模型;文献[8]将太阳总辐射的确定性模型与随机模型联合使用,建立了太阳总辐射的自回归积分滑动平均(autoregressive integrated moving average model, ARIMA)逐时模型。上述模型的基本思路均是在计及太阳辐照度时序相关性的基础上附加考虑太阳辐射的随机波动性,以此反映太阳辐照度的时序随机性或时序相关性,都忽略了日总辐照度与小时辐照度之间的“加和”约束。
传统太阳辐照度的时序变动模型中,小时辐照度一般通过半正弦模型将日总辐射按预设的时间函数逐时分配,这种机械式按确定性规律获取小时辐照度的做法显然难以准确反映小时辐照度的随机波动性特点,且未考虑日总辐照度与小时辐照度的“加和”约束。文献[9]根据解集理论建立了日总辐照度到小时辐照度的概率解集参数模型。该模型的不足在于太阳辐照度的概率分布类型事先需人为假定,而主观假定的概率分布类型与真实分布的一致性往往难以保证。鉴于此,本文基于条件核密度估计方法(conditional kernel density estimation,CKDE)建立能同时计及太阳辐照度时序随机性、日/小时辐照度之间时序相关性及内在“加和”约束的非参数概率模型。建模流程分2步:
(1)在给定日总辐照度的条件下,根据改进CKDE技术实现日总辐照度向小时辐照度的解集,以建立小时太阳辐照度的条件概率模型。
(2)计及相邻日总辐照度的强时序相关性,根据改进CKDE技术建立计及时序相关性的日总辐照度条件概率模型。
最后,通过对实测光伏发电系统辐照度数据的统计分析,并在此基础上对比传统光伏发电系统辐照度模型及本文模型对实测数据的追踪效果,验证本文模型的优越性。
1 太阳辐照度的条件概率密度估计模型
1.1 计及“加和”特性的小时辐照度条件核密度估计
令It表示第t年的日总辐照度,W/m2;r=[r1,r2,…,rd]T表示小时辐照度构成的随机向量,W/m2;显然,r1,r2,…,rd是具有随机波动性及时序相关性的随机序列(d=24)。对于m年共n天的实测数据,设第t年第i天的日总辐照度为Iti,小时辐照度样本为ri=[ri1,ri2,…,rid]T,i=1,2,…,n。则在It已知条件下,r的条件概率密度函数可表示为
(1)
式中:f(r,It)是d+1维联合概率密度函数;f(It)是It的边缘概率密度函数。f(r,It)和f(It)的分布类型事先难以确定,但根据(r,It)的n个样本,即(ri,Iti),i=1,2,…,n。根据条件核密度估计理论[10],f(r|It)可采用下式求解
(2)
式中:
(3)
(4)
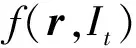
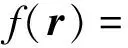
(5)

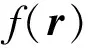
(6)
式中:tr{·}表示矩阵的迹;f"(r)为多维函数f(r)的二阶偏导数,即Hessian矩阵。
如果H采用满阵形式,其求解将是一个待求变量数为d(d1)/2的组合优化问题,在维数d较高时计算非常困难。而常规做法仅取H的对角元以简化多维联合概率密度估计的求解过程,但忽略带宽矩阵中非对角元元素又会使概率密度估计的精度在高维情况下精度变差。为权衡高维条件下多变量核密度估计中计算精度与计算复杂性的矛盾,本文带宽矩阵H的求取引入文献[12]中的带宽矩阵解析算法,令:
H=λ2S
(7)
式中S表示随机向量r的样本协方差矩阵。
将式(7)代入式(6),可得到AMISE取最小值时最优带宽系数的近似解析表达式为
λ=[nd(4π)d/2R(f)]-1/(d+4)
(8)
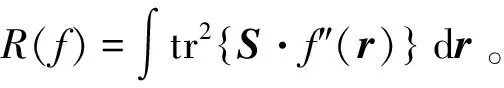
式(7)的引入不仅降低了带宽矩阵的计算复杂度,且仍可保证H为满阵,因此概率密度估计的计算精度也相对较好[13]。将求解的最优带宽矩阵代入式(5),可得式(3)(4)统一估计形式为
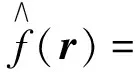
(9)
此外,日总辐照度应等于当前日小时辐照度的“加和”,即It=r1+r2+…+rd。为计及小时辐照度与日总辐照度间的“加和”特性,进行如下变换:
Y=Rr
(10)
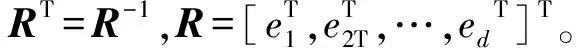

(11)
(12)


(13)

(14)

同理,将式(10)代入式(4),并结合式(13),小时辐照度的条件核密度估计即可表示为
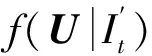
(15)
式中:
(16)
(17)

1.2 计及相关性的日总辐照度条件核密度估计
公式(15)建立了日辐照度It与小时辐照度ri的条件核密度估计,但相邻日的日总辐照度间往往也具有较强的时序相关性,因此还需建立日总辐照度之间的条件概率分布,此时相邻日总辐照度的条件核密度分布总式表述如下:
(18)
式中:f(It,It-1)是相邻日总辐照度It和It-1的联合概率密度函数;f(It-1)是It-1的概率密度函数。此时令Iti=[Iti,Iti-1]T为相邻日总辐照度构成的样本数据,样本容量为n-1。利用核密度估计理论可得f(It,It-1)和f(It-1)的密度函数估计为

(19)
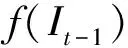
(20)
式中:λt,λt-1分别为f(It,It-1),f(It-1)核密度估计的最优带宽系数;St为It的样本协方差矩阵,可表示为
(21)
式中:Sh为It的样本方差;Shq为It和It-1的样本协方差;Sq为It-1的样本方差。
将式(19)、(20)代入式(18),即可得相邻日总辐照度服从的条件概率密度函数f(It|It-1)估计为

(22)
式中:
(23)
(24)
(25)
上述基于条件核密度估计建立了式(15)所示的小时辐照度条件概率模型和式(22)所示的日总辐照度条件概率模型。该模型避开了序列相依结构(线性或非线性相关)和概率密度函数分布类型的事先假定,充分考虑了太阳辐照度变化的时序随机性和时序相关性,且保持了日总辐照度与小时辐照度间的“加和”约束。
2 日总辐照度到小时辐照度的解集流程
在电力系统概率分析中,常常需要根据太阳辐照度的概率密度函数产生太阳辐照度时间序列的随机样本。本文利用式(22)日总辐照度条件核密度估计抽取1年365天日总辐照度的时间序列随机样本;然后基于式(15)的小时辐照度条件核密度估计实现日总辐照度到小时辐照度的非参数解集。本文提出的太阳辐照度条件概率模型涉及到2个表达式较为复杂的非参数核密度估计,因此采用文献[13]介绍的多维核密度估计高效抽样法,实现辐照度时间序列随机样本的抽取,该抽样方法详见附录A。抽样过程详述如下:

3 算例分析
3.1 算例数据
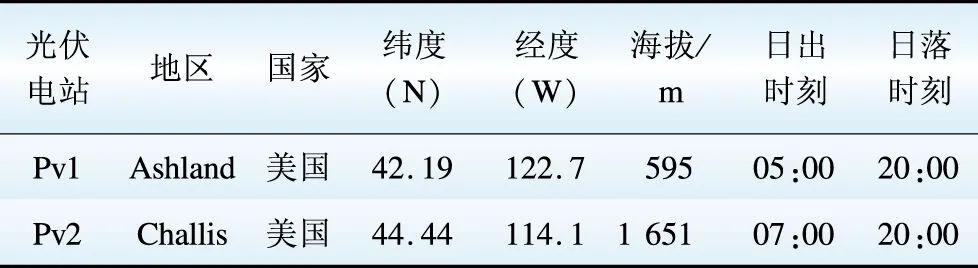
为验证本文基于条件核密度估计技术的光伏发电系统时序概率模型的有效性和准确性,以MATLAB(2016a)为仿真平台,对传统光伏发电系统模型(日辐照度服从高斯分布,小时辐照度根据半正弦模型逐时分配)及本文光伏发电系统的时序概率模型进行仿真对比,本文中,光伏电站的实测数据采用美国Oregon大学Solar Radiation Monitoring Laboratory实验室提供的Ashland和Challis地区两座光伏电站2011—2013年的小时辐照度量测数据[15],并用Pv1、Pv2分别表示上述2个光伏电站。该地区的地理位置及光照起止时刻如表1所示。其中:光伏电站额定出力为10 MW,rc为150 W/m2,rstd取值为1 000 W/m2,电站故障率及修复时间分别为0.12次/年和60 h[14]。
表1 光伏电站所在地区的地理及光照时间信息
Table 1 Geographical and radiation time information of PV sites
3.2 辐照度解集模型的应用分析
基于Pv1、Pv2光伏电站的小时辐照度实测数据,分别采用传统光伏发电系统概率模型及本文基于解集的非参数时序概率模型求解各自日总辐照度及小时辐照度的概率密度函数。因自相关系数可准确反映时间序列第t时刻与第t-k时刻下随机变量的时间相关性程度,因此,本文分别通过光伏电站实测数据及两模型抽样产生的辐照度时间序列样本计算小时辐照度的自相关系数,计算结果如图1所示(注:模型一指本文基于解集的光伏发电系统时序概率模型;模型二指传统小时辐照度服从半正弦分布,日总辐照度服从高斯分布的光伏发电系统概率模型,下同)。
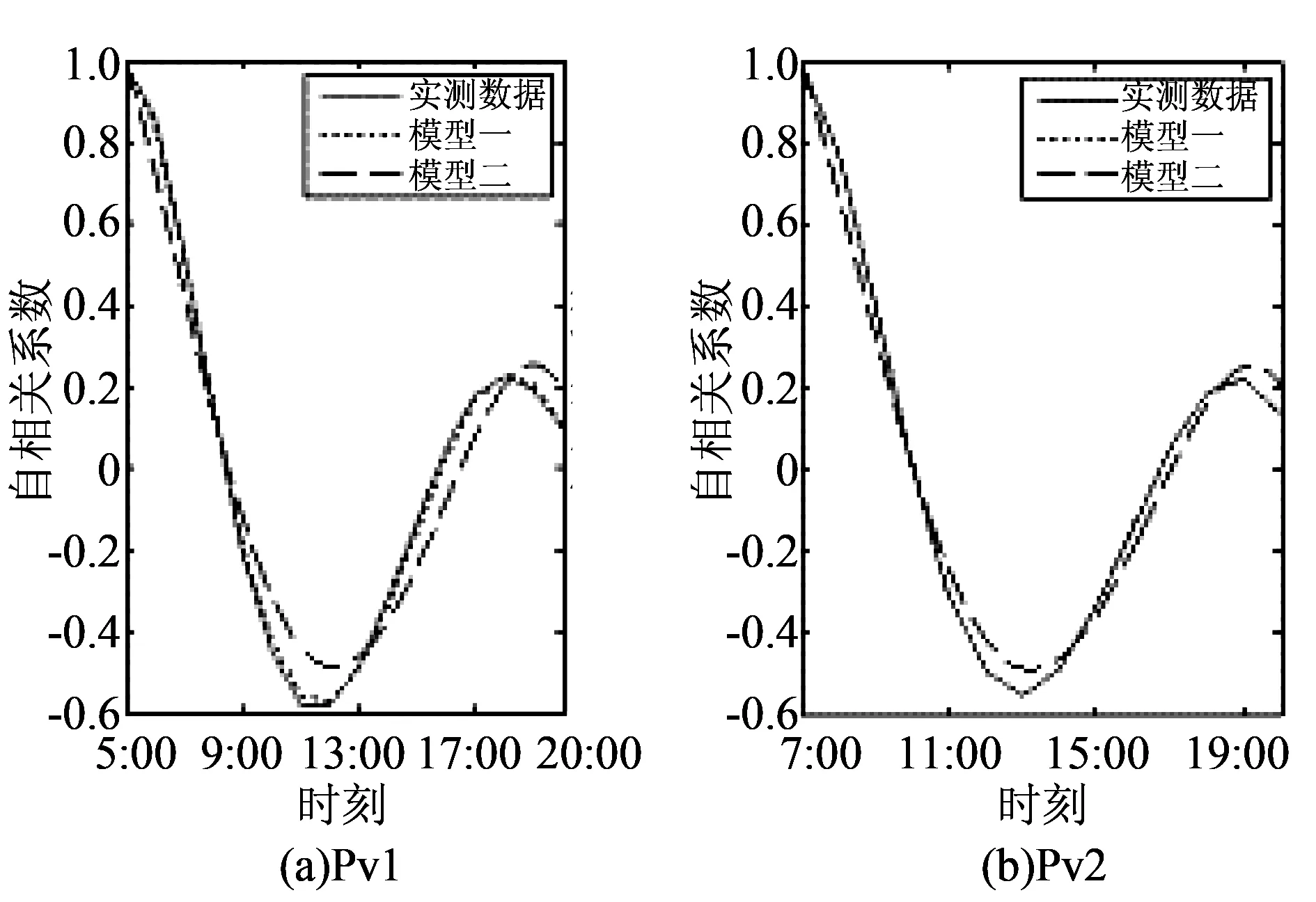
图1 光伏电站小时辐照度的自相关系数Fig.1 Autocorrelation coefficient of hourly solar radiation in photovoltaic power station
由图1知:基于本文模型抽样得到的辐照度时间序列样本相关性系数曲线,比传统光伏概率模型更贴近实测数据对应的自相关系数曲线。换言之,该时序概率模型能更准确反映1天内各小时辐照度之间的时序相关性。这主要是因为传统光伏概率模型小时辐照度仅是按半正弦模型按确定性准则逐时分配获取,小时辐照度之间的自相关性是确定的,且尚未考虑小时辐照度自身波动的随机性对自相关系数的影响。而本文基于解集的非参数条件核密度时序概率模型是在保证小时辐照度时序相关的基础上,通过解集随机获取对应小时辐照度的样本量信息,较传统概率模型而言考虑了小时辐照度自身波动的随机性问题,较传统模型而言更符合真实情况。
为进一步验证辐照度时序概率模型的准确性,本文利用2个光伏电站实测数据及两模型抽样得到的辐照度时间序列样本,逐一计算全年的小时辐照度及日总辐照度的概率密度分布曲线,如图2、3所示。
由图2、3可知:采用本文方法计算得到的小时辐照度条件概率密度分布曲线及日总辐照度概率密度分布曲线能较好地追踪实测数据的概率分布规律,而基于传统概率模型求得的小时辐照度及日总辐照度的概率密度曲线追踪效果相对较差。这在日总辐照度的概率密度分布中对比尤为明显,其主要原因在于:传统概率模型对应的日辐照度密度分布并未计及相邻日总辐照度间的时序相关性影响,且分布类型是已知的,较难刻画实际日总辐射的时序随机变化过程。不难看出:本文模型具有相对较高的模拟精度。
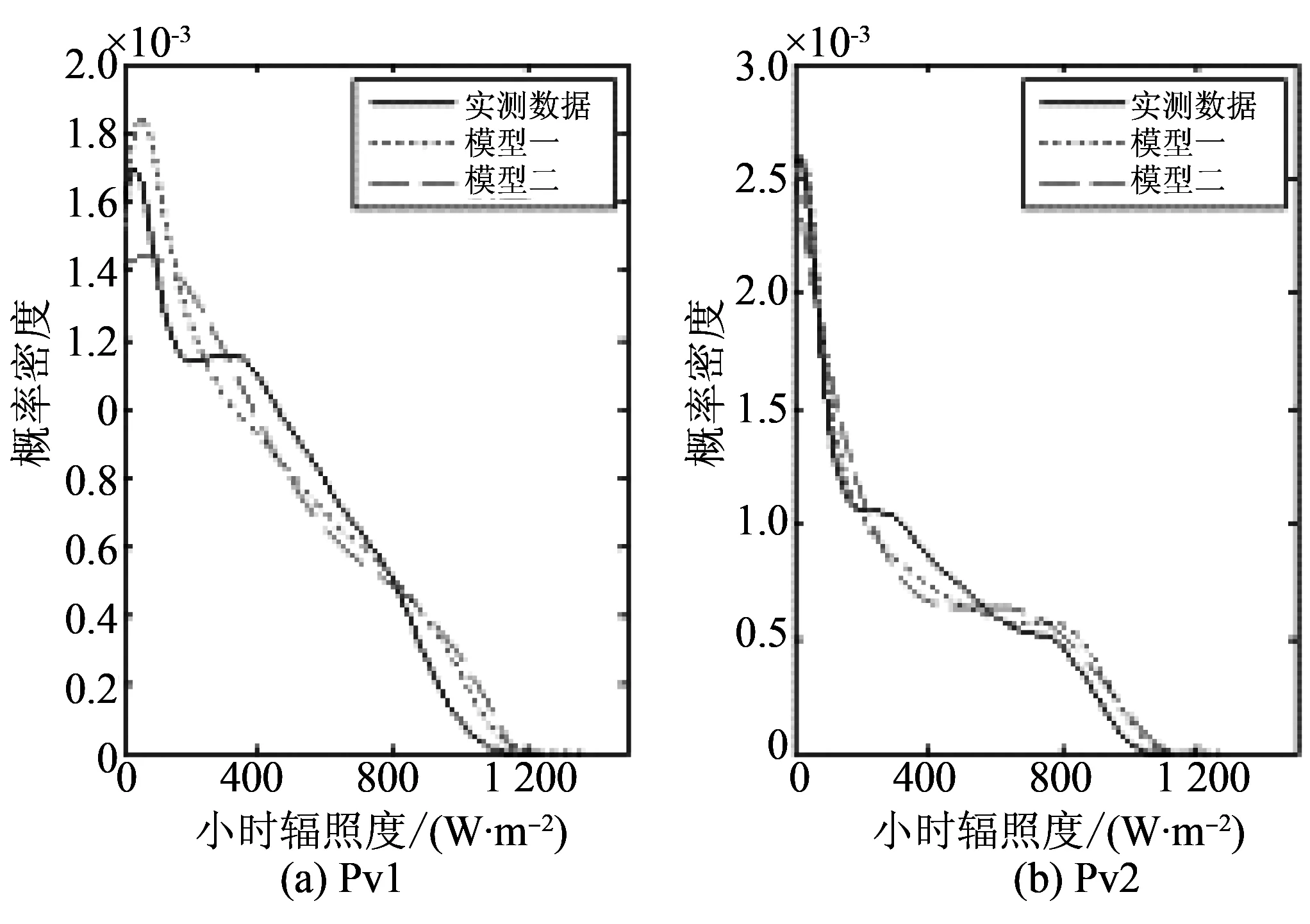
图2 光伏电站小时辐照度的概率密度分布Fig.2 Probability density distribution of hourly solar radiation in photovoltaic power station
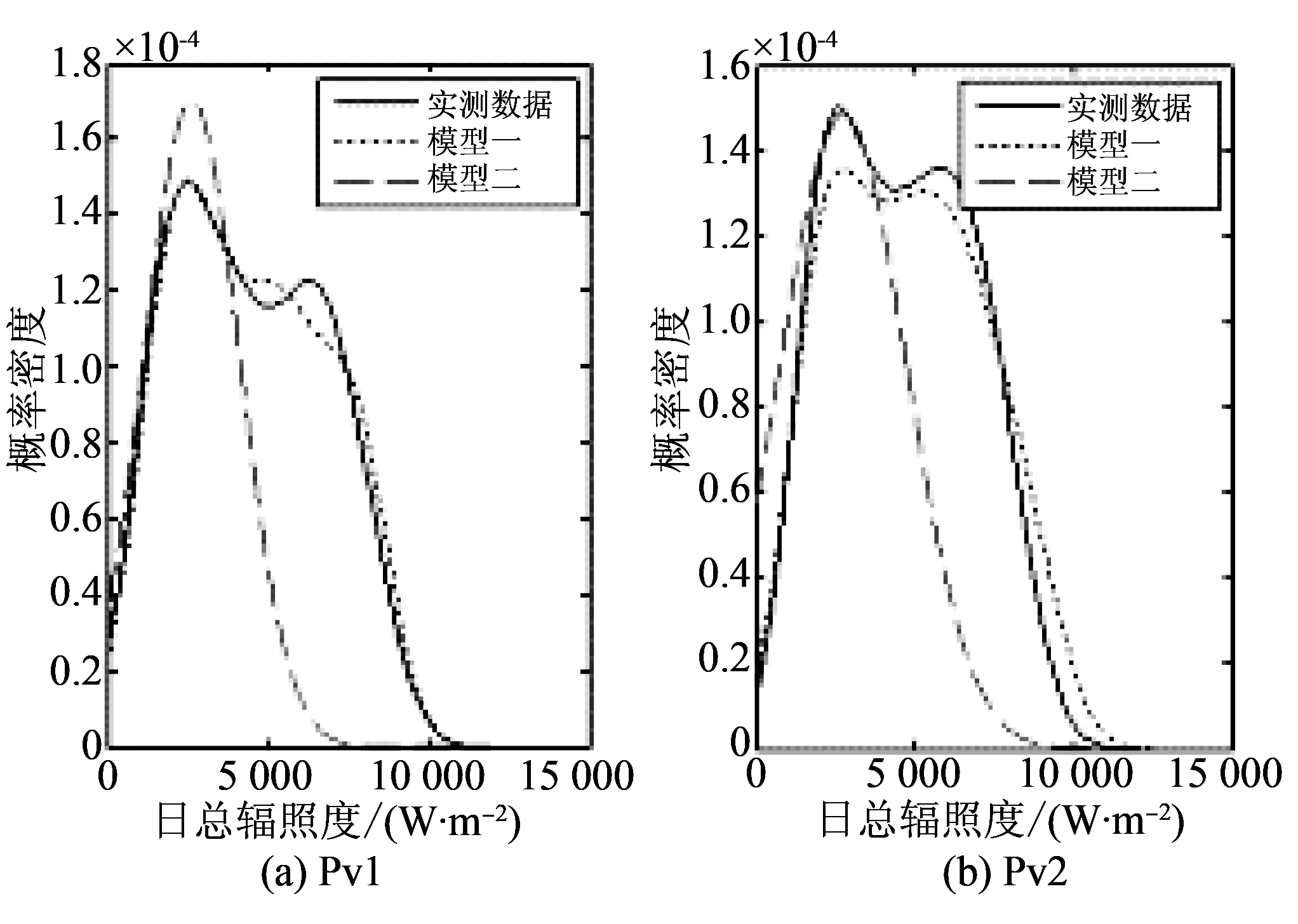
图3 光伏电站日总辐照度的概率密度分布Fig.3 Probability density distribution of daily solar radiation in photovoltaic power station
4 结 论
本文采用满阵形式的带宽矩阵推导条件核密度估计更一般的表达式,并基于改进的条件核密度估计技术建立了能同时考虑逐时辐照度随机性、时序相关性和“加和”特性的太阳辐照度条件概率模型,即小时辐照度的条件核密度估计和日总辐照度的条件核密度估计。仿真结果表明:本文方法得到的小时自相关系数与实测数据非常接近,且抽样得到的小时辐照度概率分布和日总辐照度概率分布能准确反映实测数据的随机分布规律,具有一定的参考性与实用价值。
[1]赵争鸣,刘建政,孙晓瑛,等.太阳能光伏发电及其应用[M].北京:科学出版社,2005:243-245. ZHAO Zhengming,LIU Jianzheng,SUN Xiaoying,et al.Solar energy PV generation and its application[M].Beijing:Science press,2005:243-245.
[2]KARAKI S H,CHEDID R B,RAMADAN R.Probabilistic performance assessment of autonomoussolar-wind energy conversion systems[J].IEEE Transactions on Energy Conversion,1999,14(3):766-772.
[3]ABOUZAHR I,RAMAKUMAR R.Loss of power supply probability of stand-alone photovoltaic systems:a closed form solution approach [J].IEEE Transactions on Energy Conversion,1991,6(1):1-11.
[4]AIEN M,FIRUZABAD F,RASHIDINEJAD M.Probabilistic optimal power flow in correlated hybridwind-photovoltaic power systems [J].IEEE Transactions on Smart Grid,2014,5(1):130-138.
[5]王成山,郑海峰,谢莹华,等.计及分布式发电的配电系统随机潮流计算[J].电力系统自动化,2005,29(24):39-44. WANG Chengshan,ZHENG Haifeng,XIE Yinghua,et al.Probabilistic power flow containing distributed generation in distribution system[J].Automation of Electrical Power Systems,2005,29(24):39-44 .
[6]余昆,曹一家,陈星莺,等.含分布式电源的地区电网动态概率潮流计算[J].中国电机工程学报,2011,31(1):20-25. YU Kun,CAO Yijia,CHEN Xingying,et al.Dynamic probability power flow of district grid containing distributed generation[J].Proceedings of the CSEE,2011,31(1):20-25.
[7]REN Zhouyang,YAN Wei,ZHAO Xia,et al.Chronological probability model of photovoltaic generation[J].IEEE Transactions on Power Systems,2014,29(3):1077-1088.
[8]张素宁,田胜元.太阳辐射逐时模型的建立[J].太阳能学报,1997,18(3):273-277. ZHANG Suning,TIAN Shengyuan.The institution of the hourly solar radiation model[J].Acta Energiae Solaris Sinica,1997,18(3):273-277.
[9]GRAHAM V A,HOLLANDS K G T.A method to generate synthetic hourly solar radiation globally[J].Solar Energy,1990,44(6):333-341.
[10]FAN J,YAO Q,TONG H.Estimation of conditional densities and sensitivity measures in nonlinear dynamical systems[J].Biometrika,1996,83(1):189-206.
[11]TARBOTON D G,SHARMA A,LALL U.Disaggregation procedures for stochastic hydrology based on nonparametric density estimation[J].Water Resources Research,1998,34(1):107-119.
[12]KRISTA K,LEONARDIS A,SKOCAJ D.Multivariate online kernerldesity estimation with density estimation with Gaussian kernels[J]. Pattern Recognition,2011,44(10):2630-2642.
[13]赵渊, 范飞, 杨金刚, 等. 电网可靠性评估中计及加和特性的非参数解集负荷模型[J]. 中国电机工程学报, 2015, 35(23): 6039-6047. ZHAO Yuan, FAN Fei, YANG Jingang,et al. Nonparametric disaggregation load model in power system reliability evaluation incorporating the additive correlation[J]. Proceedings of the CSEE, 2015, 35(23): 6039-6047.
[14]CHA S T,JEON D H,BASE I S,et al.Reliability evaluation of distribution system connected photovoltaic generation considering weather effects[C]//International Conference on Probabilistic Methods Applied to Power Systems.Ames,America:IEEE,2004:451-456.
[15]University of Oregon Solar Radiation Monitoring Laboratory. The hourly PV power data[DB/OL].(2013-08-09)[2016-06-17].http://solardat.uoregon.edu/SolarData.html.
[16]李江,刘伟波,李国庆,等. 基于序贯蒙特卡罗法的复杂配电网可靠性分析[J]. 电力建设,2015,36(11):17-23. LI Jiang, LIU Weibo, LI Guoqing, et al. Reliability analysis of complex distribution network based on sequential Monte Carlo method[J]. Electric Power Construction, 2015,36(11):17-23.
[17]栾伟杰,蒋献伟,张节潭,等. 考虑主动管理的分布式光伏发电消纳能力研究[J]. 电力建设,2016,37(1):137-143. LUAN Weijie, JIANG Xianwei, ZHANG Jietan, et al. Consumptive ability analysis for distributed photovoltaic generation considering active management[J]. Electric Power Construction, 2016,37(1):137-143.
[18]周楠,刘念,张建华. 考虑多种上网价格规制的光伏微网运营对比研究[J]. 电力建设,2016,37(3):82-89. ZHOU Nan, LIU Nian, ZHANG Jianhua. PV-based microgrid operation contrastive research considering on-grid power tariff regulation t[J]. Electric Power Construction, 2016,37(3):82-89.
(编辑 蒋毅恒)
附录A
假若d维随机向量X有n个样本数据Xi,样本协方差矩阵为Sx,i=1,2,…n。随机向量X的核密度估计函数可表示为
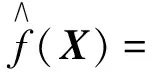
(A1)
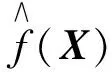
(1)随机抽取一个[0,1]间均匀分布的随机数r。
(2)根据n个高斯核函数的权重之和为1,即∑ωi=1,将[0,1]区间分成n个长度分别为ωi的子区间,并通过判断r落在子区间的位置确定抽取的高斯函数。该高斯函数的均值为Xr、协方差矩阵为λx2Sx。
(3)抽样生成d1维的高斯向量V,且每个元素独立同分布于N~(0,1),对矩阵Sx进行Cholesky分解,使Sx=PPT,则可得d维随机向量X=Xr+λxPV。
Chronological Probability Model of Photovoltaic Generation System
JIN Liming1, ZHOU Ning1, FENG Li1, FAN Fei2,ZHAO Yuan2
(1. State Grid Chongqing Electric Power Company, Chongqing 400015, China; 2. State Key Laboratory of Power Transmission Equipment & System Security and New Technology (Chongqing University), Chongqing 400044, China)
With the growing use of photovoltaic (PV) generation in power system, establishing effective probabilistic model for PV generation becomes an urgent problem to be settled. Conventional chronological probability models of PV generation are based on parametric estimation, which require to assume the probability distribution type of irradiance, and cannot consider the ’additive constraint’ between day’s and hour’s irradiance sequence. In order to overcome the drawbacks of conventional models, this paper proposes a new photovoltaic sequence probabilistic model based on disaggregation theory and conditional kernel density estimation. Without limiting the probability distribution type of irradiance, the proposed nonparametric model is the non-parametric model, and can capture not only the chronological correlation, but also the ’additive constraint’ between day’s and hour’s irradiance sequence, which can more accurately reflect the random fluctuation law of photovoltaic generation. The example analysis shows that the model can reflect the change rule of irradiance with higher precision, which has obvious superiority and practicality.
photovoltaic generation; probabilistic model; additive constraint; chronological correlation;conditional kernel density estimation
国家自然科学基金项目(50977094)
TM 732
A
1000-7229(2016)07-0027-06
10.3969/j.issn.1000-7229.2016.07.004
2016-02-07
金黎明(1982),男,硕士,高级工程师,长期从事电力系统运行分析和控制的研究工作;
周宁(1972),男,硕士,高级工程师,长期从事电力系统自动化研究工作;
冯丽(1975),女,博士,高级工程师,长期从事电力系统运行分析和控制研究工作;
范飞(1989),男,硕士研究生,从事电力系统规划与可靠性的研究工作;
赵渊(1974),男,教授,博士生导师,长期从事电力系统规划与可靠性的研究工作。
Project supported by National Natural Science Foundation of China(50977094)

